基于修正黏性摩擦LuGre模型的比例多路阀摩擦补偿

陈东宁 刘一丹 姚成玉 蒋栋林 王可勋1．燕山大学河北省重型机械流体动力传输与控制实验室，秦皇岛，0660042．先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛，066004．燕山大学河北省工业计算机控制工程重点实验室，秦皇岛，066004

基于修正黏性摩擦LuGre模型的比例多路阀摩擦补偿

陈东宁1,2刘一丹1,2姚成玉3蒋栋林1,2王可勋1,2
1．燕山大学河北省重型机械流体动力传输与控制实验室，秦皇岛，0660042．先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛，0660043．燕山大学河北省工业计算机控制工程重点实验室，秦皇岛，066004

为减小摩擦对比例多路阀性能的影响，提出基于修正黏性摩擦LuGre模型的比例多路阀摩擦特性分析、模型参数辨识以及摩擦补偿方法。通过实验测试间接得出摩擦数据，运用数据拟合方法辨识出修正黏性摩擦LuGre模型的静态和动态参数。基于辨识参数设计出修正黏性摩擦LuGre模型摩擦状态观测器，将观测器摩擦信号输出量反馈到控制模型输入端，减小摩擦对比例多路阀性能的不良影响。仿真结果表明，基于辨识参数的修正黏性摩擦LuGre模型摩擦补偿方法可提高比例多路阀的位置跟踪精度。

比例多路阀；摩擦补偿；LuGre模型；黏性摩擦；参数辨识

0 引言

摩擦是影响比例多路阀静动态性能的重要因素，是造成阀芯卡涩卡滞、低速爬行、流量滞环大、极限环振荡以及微动特性差等现象的主要原因，尤其在阀芯开启、关闭以及阀芯换向时摩擦的影响最为严重[1-2]。比例多路阀特性直接关系到液压系统的运行性能，因此，对比例多路阀进行摩擦特性分析和摩擦补偿的研究具有重要意义。

目前摩擦补偿的方法主要有基于摩擦模型的补偿、不依赖于摩擦模型的补偿、基于智能控制策略的摩擦补偿以及复合控制策略的摩擦补偿等。常用的摩擦模型有库仑摩擦模型、Stribeck摩擦模型、LuGre摩擦模型等。为了消除摩擦不稳定现象，一个精确的摩擦模型是必要的，一个好的摩擦模型需集成多个摩擦问题研究中的重要现象[3]。由于LuGre模型能够全面、精确地描述预滑动位移、摩擦滞环、变化的临界摩擦、爬行以及Stribeck效应等各种摩擦静动态特性，故已成为当前摩擦补偿最常采用的一种摩擦模型[4-6]。文献[7]提出了一种一次性获得模型所有参数的新型快速识别方法，求解出了相应的LuGre离散递推方程，解决了参数辨识时无法有效检测鬃毛微位移的难题。文献[8]提出在运动逆转和运动停止时，与滞后相关的摩擦阻尼是作为精确定位控制最重要的部分，对摩擦的效果起到很关键的作用。文献[9]对比了基于LuGre摩擦模型和基于经典库仑+黏滞摩擦模型计算所得的泵柱塞弹性位移，结果表明，基于LuGre摩擦模型计算得到的抽油泵泵效更接近生产实际。文献[10]根据LuGre模型，构造了一个非线性观测器来估计摩擦，减小了摩擦对伺服系统性能的影响。文献[11]针对LuGre摩擦模型参数耦合动态参数辨识困难等问题，提出了一种基于区间分析的LuGre摩擦模型动态参数辨识方法。文献[12]通过李雅普诺夫稳定性分析方法，设计了基于LuGre模型的非线性摩擦自适应补偿算法，在线辨识出摩擦模型参数，并据此构造了双闭环状态观测器，补偿机电伺服系统所受的摩擦。文献[13]根据实验平台速度较高时，随速度增加摩擦增长趋势减缓的现象，建立了修正黏性摩擦的LuGre模型。

本文针对负载敏感比例多路阀提出了一种基于修正黏性摩擦LuGre模型的固定参数摩擦补偿方法。比例多路阀中使用的增加颤振信号的方法在颤振频率和幅值选取合适时可在一定程度减小摩擦对阀芯运动特性的不利影响，但该方法没有考虑摩擦与阀芯速度之间的关系，补偿效果有待提高。为此，本文首先通过实验的方法求解阀芯所受摩擦与阀芯速度的关系，进而研究基于修正黏性摩擦LuGre模型的比例多路阀摩擦补偿方法并进行仿真分析，以提高比例多路阀的位置跟踪精度。

1 比例多路阀实验测试

由于通过实验无法直接测试负载敏感比例多路阀阀芯摩擦，故需要通过采集实验数据进行摩擦的间接计算，获得摩擦与阀芯运动位移、运动速度以及加速度之间的关系数据。比例多路换向阀可以由多联组成，现对一联进行测试，实验测试液压系统原理如图1所示。

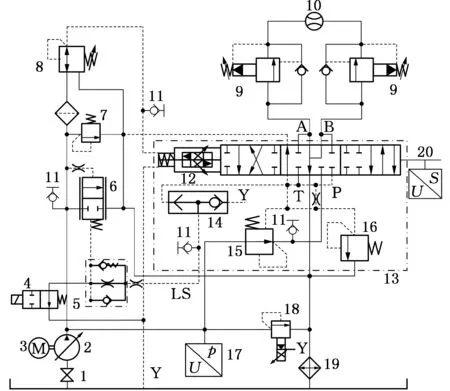
1.蝶阀 2.变量泵 3.电机 4.换向阀 5.标准阻尼元件6.三通流量补偿器 7.安全溢流阀 8.三通减压阀9.节流阀 10.流量计 11.测压接头 12.比例减压阀13.比例多路阀换向块 14.梭阀 15.二通流量补偿器16.插装式二次溢流阀 17.压力传感器 18.比例溢流阀19.冷却器 20.位移传感器图1 实验测试液压系统原理图Fig. 1 Schematic diagram of experimental test

实验测试系统主要有三条油路。第一路：变量泵2出来的压力油，经比例溢流阀18调定压力后经过二通流量补偿器15，使换向阀主阀口的压差恒定为0.6 MPa。压力油进入主阀P口，A、B口为负载口，回油经冷却器19流回油箱。第二路：压力油进入三通流量补偿器6，该阀与梭阀14配合，使泵出口压力比最大负载压力始终高0.9 MPa。第三路：压力油进入三通减压阀8，为比例减压阀12提供2.5 MPa的先导控制油，再经比例减压阀，为主阀芯提供控制油压力。

比例多路阀主阀结构如图2所示。实验测试主阀及传感器连接如图3所示。

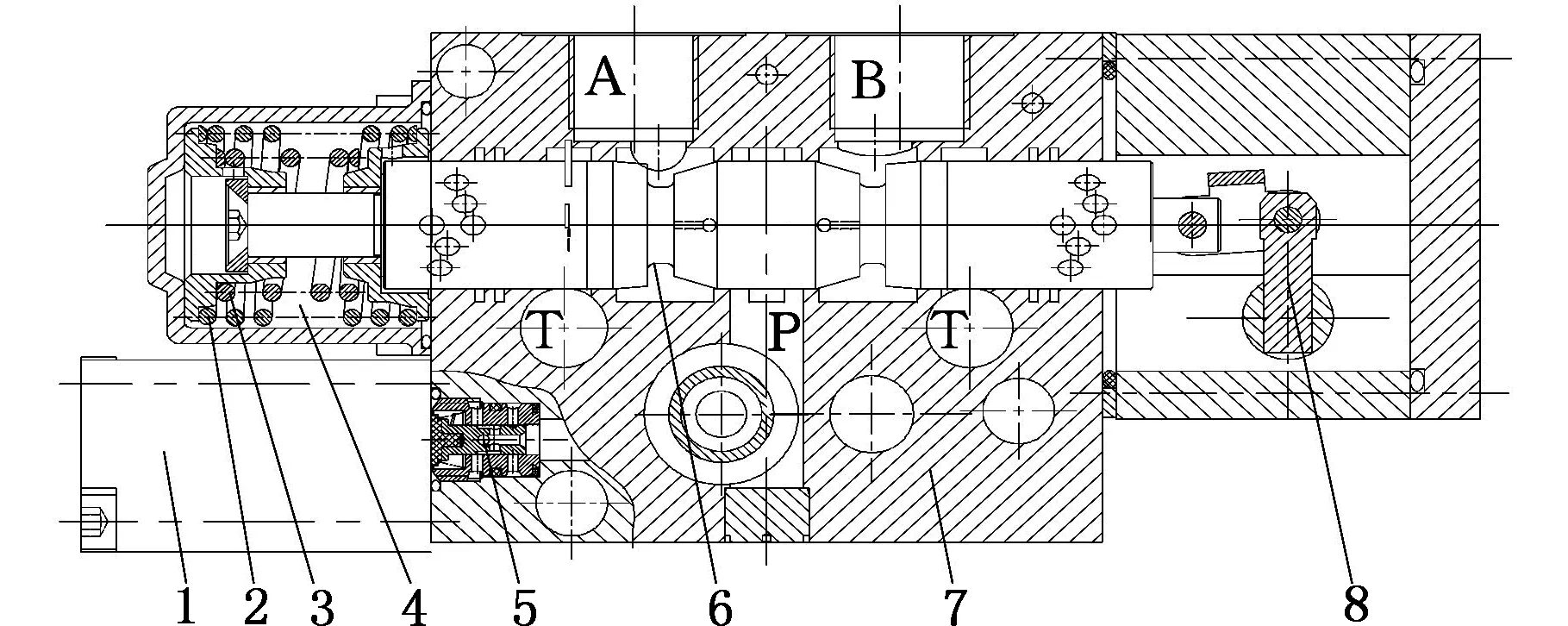
1.比例电磁铁 2.外弹簧 3.内弹簧 4.主阀控制腔5.比例减压阀 6.主阀芯 7.阀体 8.手柄图2 多路阀主阀结构Fig. 2 Main valve structure of the multi-way valve

图3 实验测试照片Fig. 3 Photograph of experimental test

利用HPM便携式数据采集仪采集各油口的压力数据，利用NI数据采集卡采集输入电流、阀芯位移、流量数据。根据实验测试要求利用LabVIEW实现控制信号输入、数据采集、测试曲线显示以及数据存储等功能。

实验采集的数据往往带有噪声信号，在对采集数据进行理论分析前，需要去除噪声信号，将有用信号提取出来。采用小波变换进行数据消噪。图4、图5为对2.2～2.3 V(阶跃值0.1 V)阶跃控制信号P口油液压力数据消噪前后时域对比图,图6、图7为消噪前后频域对比图。

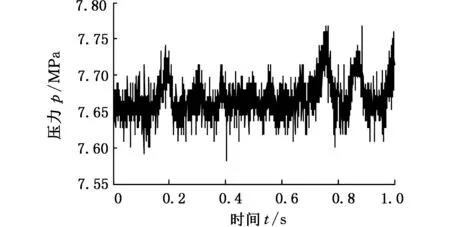
图4 原始数据的压力信号时域图Fig. 4 Time-domain diagram of original pressure signals

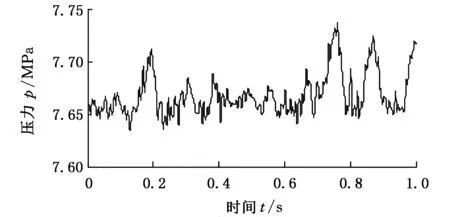
图5 消噪后的压力信号时域图Fig. 5 Time-domain diagram of de-noised pressure signals

图6 原始数据的信号功率谱密度Fig. 6 Power spectral density diagram of original signals

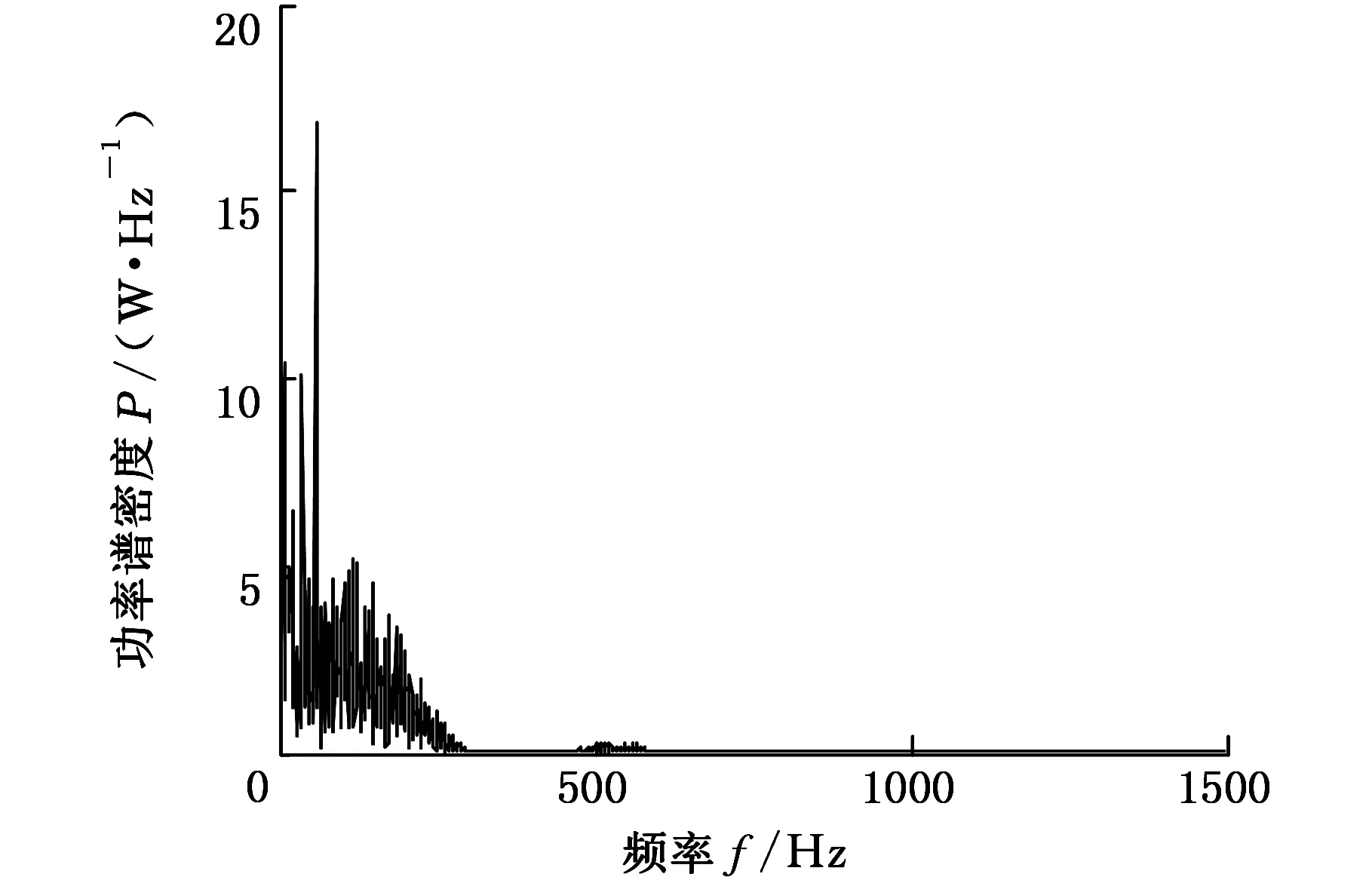
图7 消噪后的信号功率谱密度Fig. 7 Power spectral density diagram of de-noised signals

数据消噪后，通过采集的数据进行摩擦的间接计算。由于阀芯开启时微动特性的影响，阀芯加速度较小，瞬态液动力较小，故将其忽略。主阀芯上的力主要有驱动力、内外弹簧作用力、稳态液动力、惯性力以及摩擦力等，其力平衡表达式为

(1)

式中，Fi为驱动力;m为主阀芯等效质量;x为阀芯位移;Fbs为阀芯稳态液动力;Ft为内外弹簧的作用力;Ff为摩擦力。

通过对各传感器采集来的信号进行处理和计算，应用式(1)求出摩擦数据。

2 修正黏性摩擦LuGre模型的参数辨识

在获取大量实验数据的基础上，对比例多路阀摩擦进行基于修正黏性摩擦LuGre模型的参数辨识，得出摩擦与阀芯速度的关系。

2.1 LuGre模型

LuGre摩擦模型把两个刚体间的接触假定为粗糙面间的接触，将这种接触形象地表述为两刚体通过弹性鬃毛的接触，当施加外力时，接触表面近似弹性鬃毛的作用力表现为一种类似弹簧的弹性力，将微观鬃毛的变形简化为用一个弹簧和一个阻尼组成的简单系统来分析[14]，模型结构如图8所示。

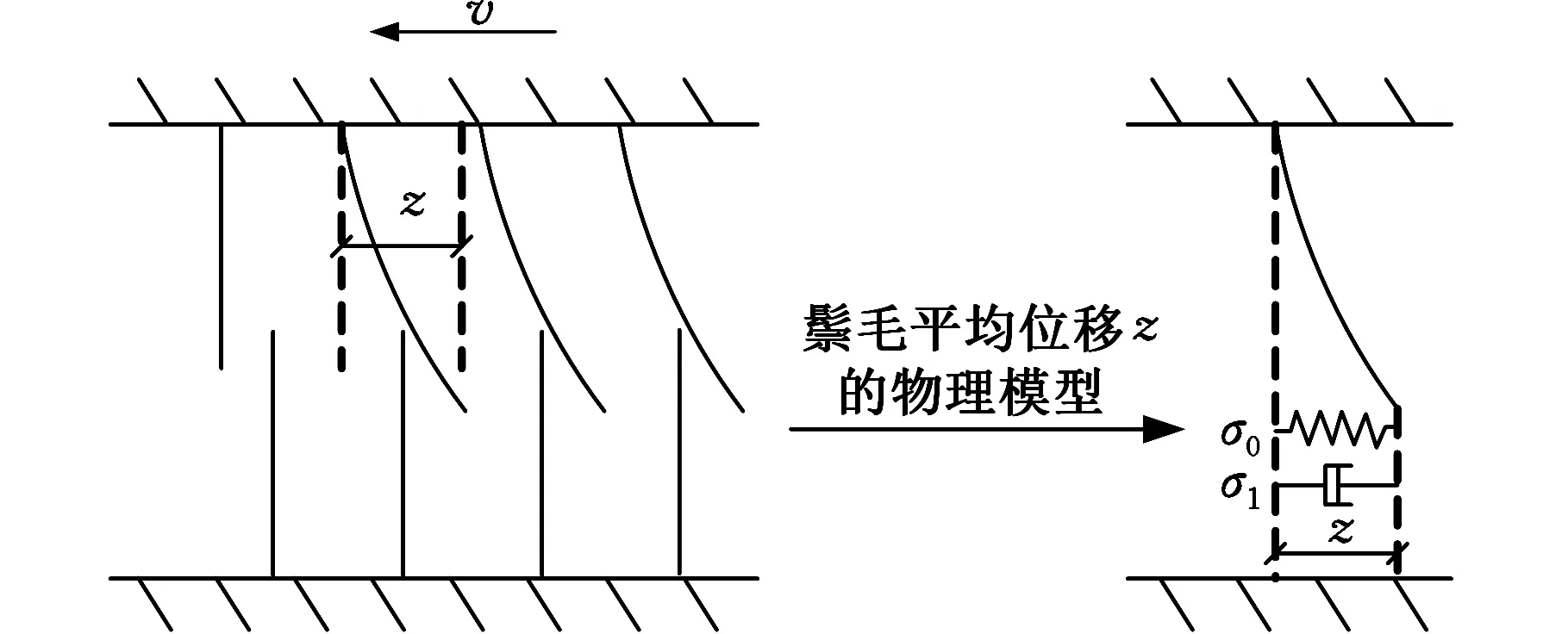
图8 LuGre摩擦模型结构示意图Fig. 8 Structure diagram of the LuGre model

摩擦力Ff可以用LuGre模型描述为

(2)

(3)

σ0g(v)=Fc+(Fs-Fc)e-(v∕vs)2

(4)

式中,σ0为鬃毛的刚度系数；z为鬃毛的平均位移；σ1为阻尼系数；σ2为黏性摩擦系数；v为刚体相对运动速度；Fc为库仑摩擦力；Fs为静摩擦力；vs为Stribeck效应速度；g(v)为大于0的函数，且有界。

当系统处于稳态，即dz/dt=0时，鬃毛的稳态平均位移zss为

(5)

稳态摩擦力Fss和速度v的关系表示为

Fss(v)=σ0g(v)sgn(v)+σ2v=
Fcsgn(v)+(Fs-Fc)e-(v/vs)2sgn(v)+σ2v

(6)

式中，σ2、Fc、Fs、vs为静态参数，σ0为动态参数。

2.2 修正黏性摩擦LuGre模型

从式(2)可以看出，LuGre模型摩擦力包括三部分，前两部分属于非黏性摩擦部分，最后一部分属于黏性摩擦部分。在高速阶段，LuGre模型中的黏性摩擦部分是与速度成线性关系的。而实际高速阶段黏性摩擦部分有随着速度增大其增长趋势减缓的现象，因此应用修正黏性摩擦的LuGre模型。该修正模型可表述为

(7)

(8)

σ0g(v)=Fc+(Fs-Fc)e-(v∕vs)2

(9)

式中，σ3为黏性摩擦斜率因子；σ4为黏性摩擦变化因子。

σ3、σ4、Fc、Fs、vs是待辨识的静态参数。σ0、σ1为待辨识的动态参数。上述摩擦模型描述了摩擦接触面内部不可测量状态变量z的动态特性，状态变量z可描述边界润滑摩擦过程中摩擦接触面的相对变形。

2.3 基于非线性最小二乘法的静态参数辨识

非线性最小二乘法是以误差的平方和最小为准则来估计非线性模型参数的一种方法。据非线性最小二乘法理论，对计算获得的摩擦力和速度数据进行曲线拟合。在拟合前需要对各静态参数初始值进行设置，以使拟合效果最佳，Stribeck速度vs为实验曲线最低点所对应速度；阀芯的相对运动速度在vs以上时，摩擦力与相对运动速度之间关系近似为一条直线；直线在y轴的截距近似为库仑摩擦力Fc的值；斜率近似为黏性摩擦系数σ2的值；最大静摩擦力Fs为主阀芯零速时的摩擦力。分别对LuGre模型和修正黏性摩擦LuGre模型进行参数识别，如图9所示。

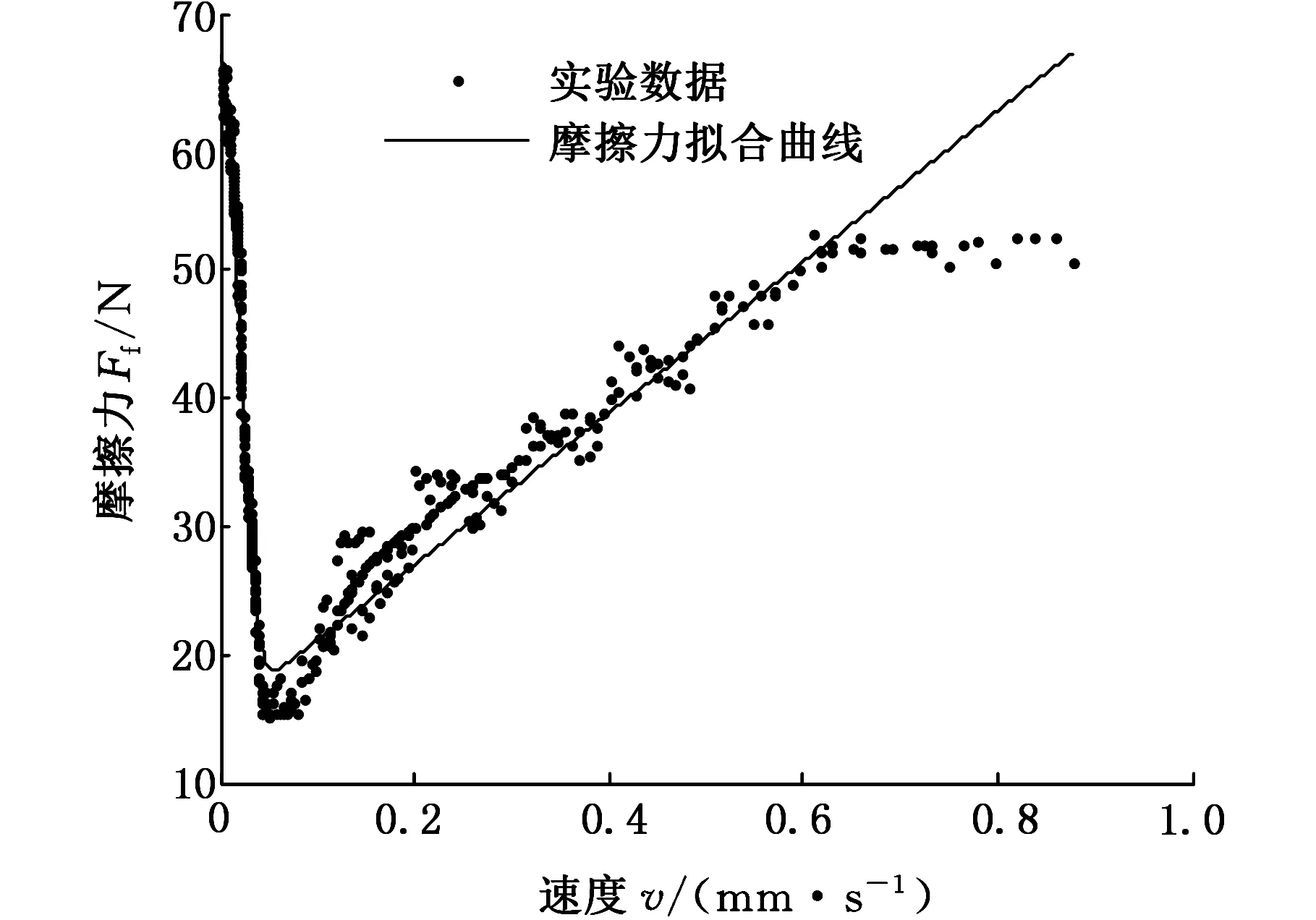
(a)LuGre模型

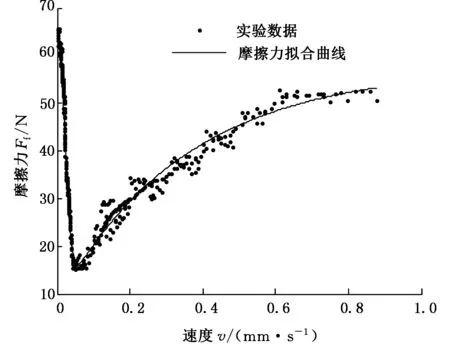
(b)修正黏性摩擦LuGre模型图9 摩擦力与阀芯速度曲线Fig. 9 Curves of friction according to the spool velocity

从图9中可以看出，修正黏性摩擦LuGre模型在曲线最低点处(Stribeck效应速度)的拟合效果比LuGre模型的拟合效果好。在较高速度阶段(0.6～0.87 mm/s)时，修正黏性摩擦LuGre模型的拟合效果也比LuGre模型的拟合效果好，它反映了阀芯速度较高时摩擦力随速度增大其增长趋势减缓的特性，对摩擦力的估计更为准确。

LuGre模型和修正黏性摩擦LuGre模型辨识参数对比如表1所示。

表1 两种模型静态辨识参数对比
Tab.1 Comparison of two models’ static identification parameters

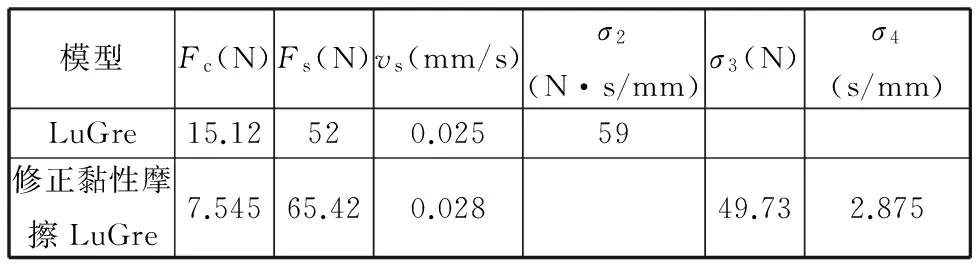
模型Fc(N)Fs(N)vs(mm/s)σ2(N·s/mm)σ3(N)σ4(s/mm)LuGre15.12520.02559修正黏性摩擦LuGre7.54565.420.02849.732.875

2.4 修正黏性摩擦LuGre模型动态参数辨识

模型的两个动态参数σ0和σ1从物理意义上讲，σ0是LuGre模型鬃毛的刚度系数，σ1是模型的阻尼系数，两参数与阀芯运动位移相关。在预滑动阶段，摩擦力表现为与阀芯相对运动位移的关系，将鬃毛模型中的平均位移z近似为阀芯的位移x，即

(10)

在阀芯微小位移内，忽略鬃毛微小变形所产生的弹性力变化；在实验测试时发现换向过程中流量传感器检测到的流量变化非常微小，故忽略液动力的影响；由于在微滑动阶段惯性力很小，故也将其忽略。输入的驱动力主要克服摩擦的影响，所以可以建立力平衡公式为

σ0x+σ1v+σ3(1-e-σ4v)=Fi

(11)

式(11)第三项中参数σ3、σ4已经获得，因此只需要辨识σ1和σ0。对主阀进行微动特性实验研究，采集阀芯0.01～0.08 mm微小位移下的实验数据，通过研究小阶跃信号下密封材料发生微小变形时摩擦力的变化，来获得相应动态摩擦参数，得出σ0= 60.56 N/mm、σ1=473 N·s/m。

3 基于修正黏性摩擦LuGre模型的摩擦补偿

AMESim软件为多学科领域复杂系统建模仿真平台，其内置液压库可用于建立比例减压阀、主阀、负载液压缸等模型，并且可以设置主阀阀芯的摩擦力参数。Simulink软件基于模型框图的图形用户界面，可使修正黏性摩擦LuGre模型状态观测器的设计更加简洁便利。为此，利用AMESim和Simulink联合仿真技术对比例多路阀进行摩擦补偿的建模与仿真。

3.1 摩擦补偿控制器设计

基于修正黏性摩擦LuGre模型的摩擦补偿控制原理如图10所示。

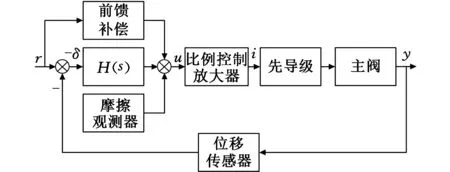
图10 摩擦补偿控制框图Fig.10 Control block diagram of friction compensation

图10中摩擦观测器根据主阀位移和误差对实际摩擦力进行估计，摩擦力估计值作为摩擦补偿量，前馈补偿根据期望位置信号计算前馈补偿量，H(s)控制环节根据位置误差信号计算误差补偿量[15]，从而有：控制量等于前馈补偿部分与H(s)控制器输出及摩擦补偿之和。

定义位置跟踪误差为：δ=y-r，位置误差系数为k0,由于摩擦模型中的鬃毛形变量不可直接测量，需要通过设计摩擦状态观测器进行评估[16],因此设计鬃毛观测器如下：

(12)

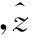
从而有摩擦观测器如下：

(13)

设计系统控制律如下：

(14)

其中，mts2r是前馈补偿，控制器H(s)采用下式:

H(s)=kP+kDs+kI/(τs+1)

(15)

式中，kP、kI、kD分别为比例、积分、微分系数。

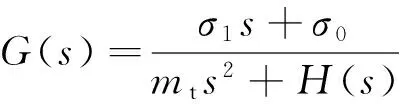
3.2 比例多路阀AMESim参数化建模

构建比例多路阀结构参数化AMESim模型，如图11所示。

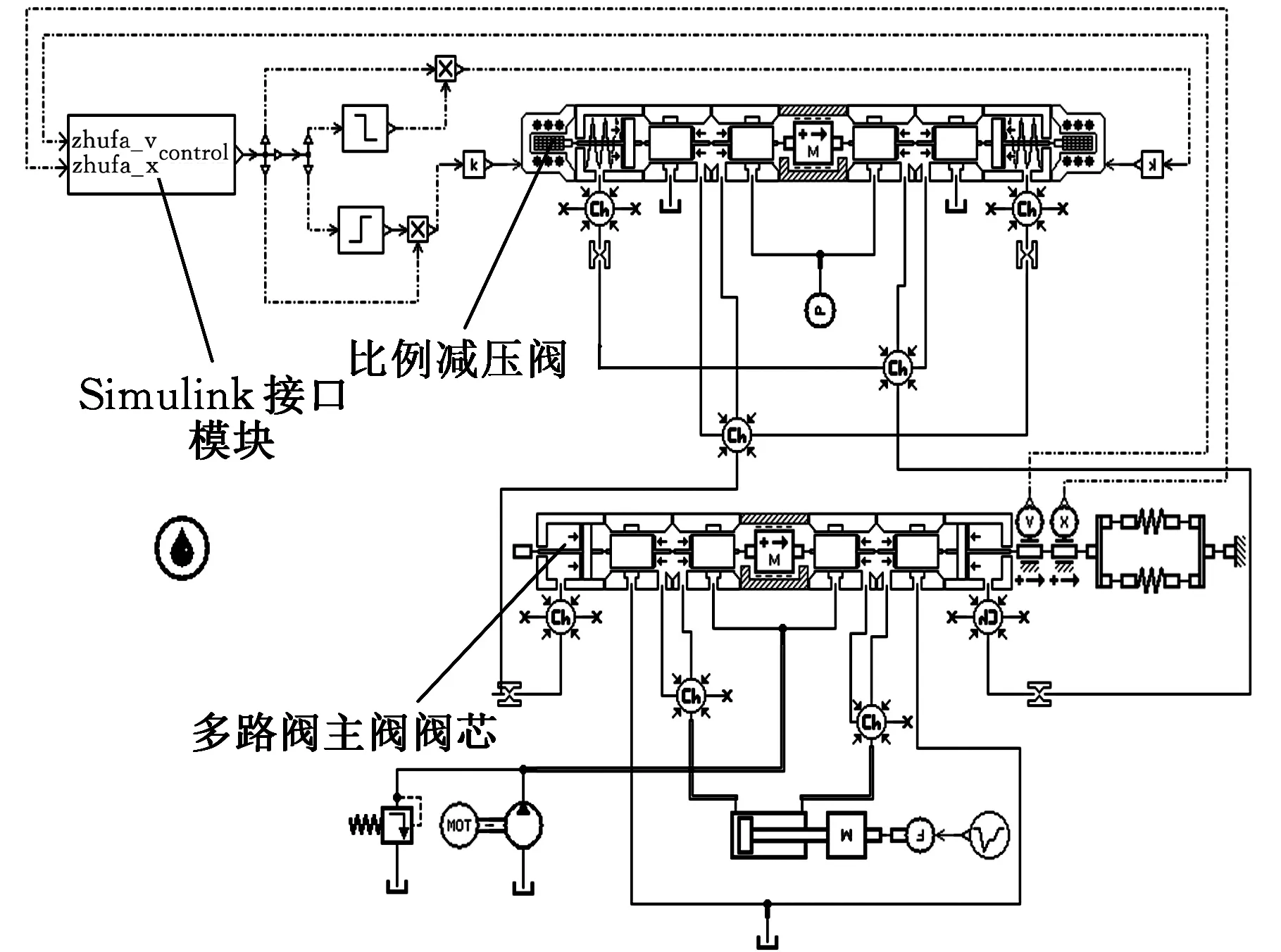
图11 比例多路阀AMESim仿真模型Fig.11 AMESim simulation model of the proportional multi-way valve

3.3 摩擦观测器的建模

根据修正黏性摩擦LuGre模型式(7)～式(9)，利用Simulink搭建摩擦状态观测器，如图12所示。

将摩擦补偿控制器的模型封装后，加入到比例多路阀的前向通道中，同时将AMESim中建立的比例多路阀结构化模型导入到Simulink中，建立AMESim/Simulink联合仿真模型,如图13所示。

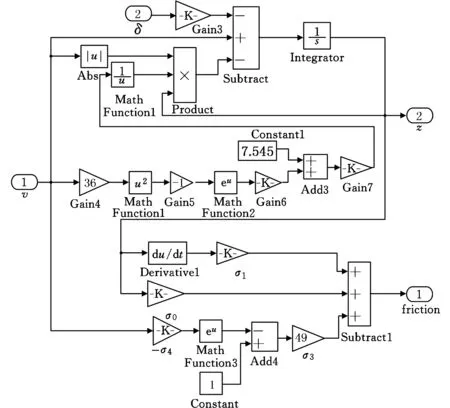
图12 修正黏性摩擦LuGre模型状态观测器Fig.12 State observer of the modified viscous friction LuGre model

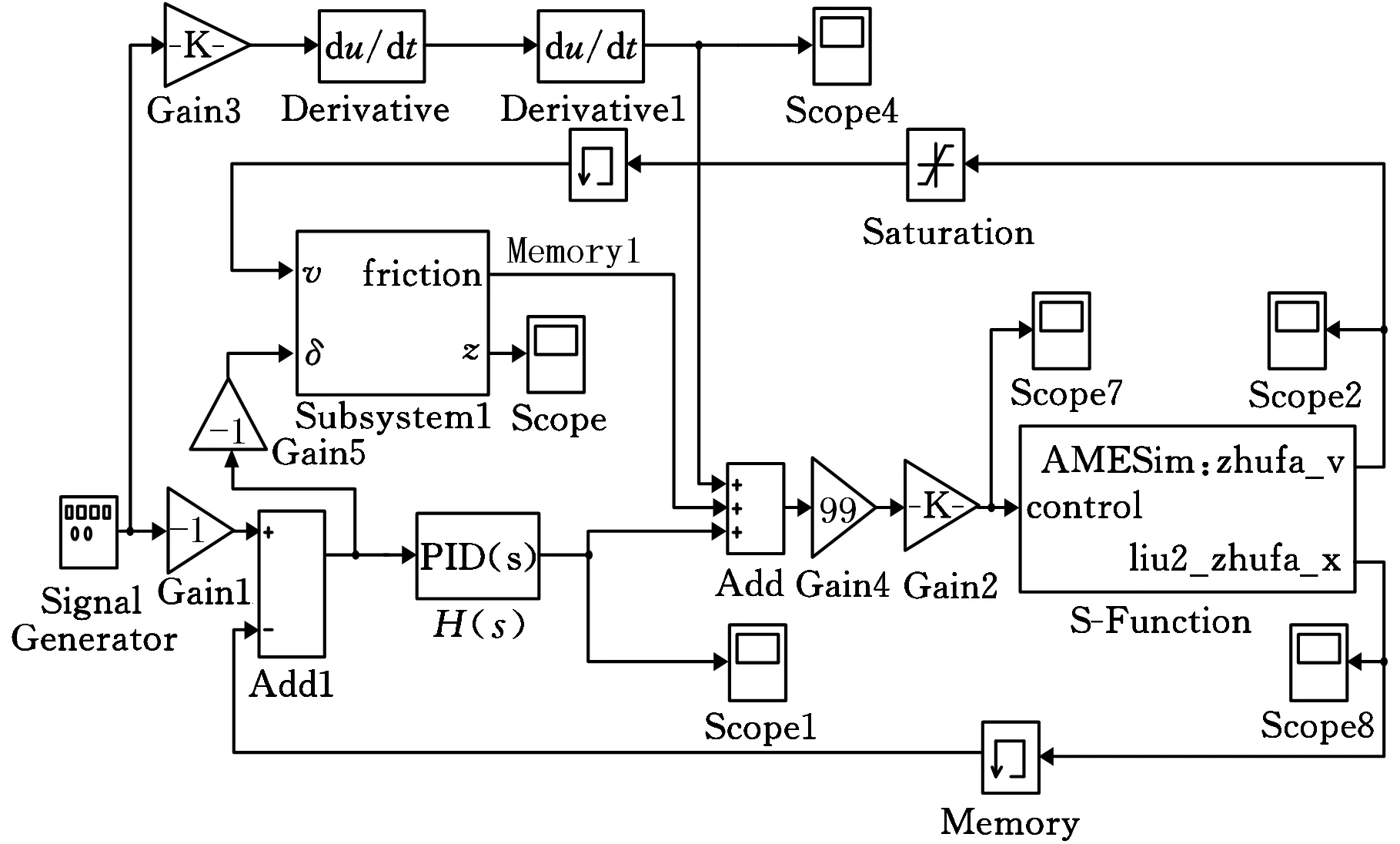
图13 比例多路阀摩擦补偿联合仿真模型Fig.13 Co-simulation model of friction compensation for the proportional multi-way valve

3.4 摩擦补偿仿真分析

比例多路阀在低速或变向运动时，仅采用PID控制器往往难以满足控制精度。所以针对修正黏性摩擦LuGre模型设计了摩擦状态观测器，进而，采用修正黏性摩擦LuGre模型进行摩擦补偿，并与PID控制器补偿方法进行仿真对比。PID控制器补偿结构如图14所示。

图14 PID控制的补偿结构图Fig.14 Compensation structure diagram of PID control

常规PID控制进行仿真时，kP=150，kI=271，kD=0.96。AMESim程序中比例多路阀主要结构参数如表2所示。

输入幅值为±0.0081 m、频率为2 Hz的方波信号，仿真时间为1 s，仿真采样时间为0.01 s，负载力为80 kN。修正黏性摩擦LuGre模型的摩擦补偿和PID控制两种方法的位置跟踪曲线如图15所示。

表2 比例多路阀主阀参数
Tab.2 Main valve parameters of the multi-way valve

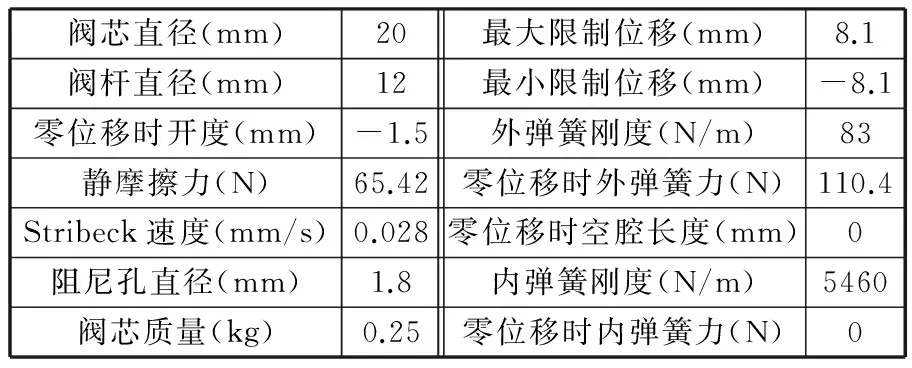
阀芯直径(mm)20最大限制位移(mm)8.1阀杆直径(mm)12最小限制位移(mm)-8.1零位移时开度(mm)-1.5外弹簧刚度(N/m)83静摩擦力(N)65.42零位移时外弹簧力(N)110.4Stribeck速度(mm/s)0.028零位移时空腔长度(mm)0阻尼孔直径(mm)1.8内弹簧刚度(N/m)5460阀芯质量(kg)0.25零位移时内弹簧力(N)0

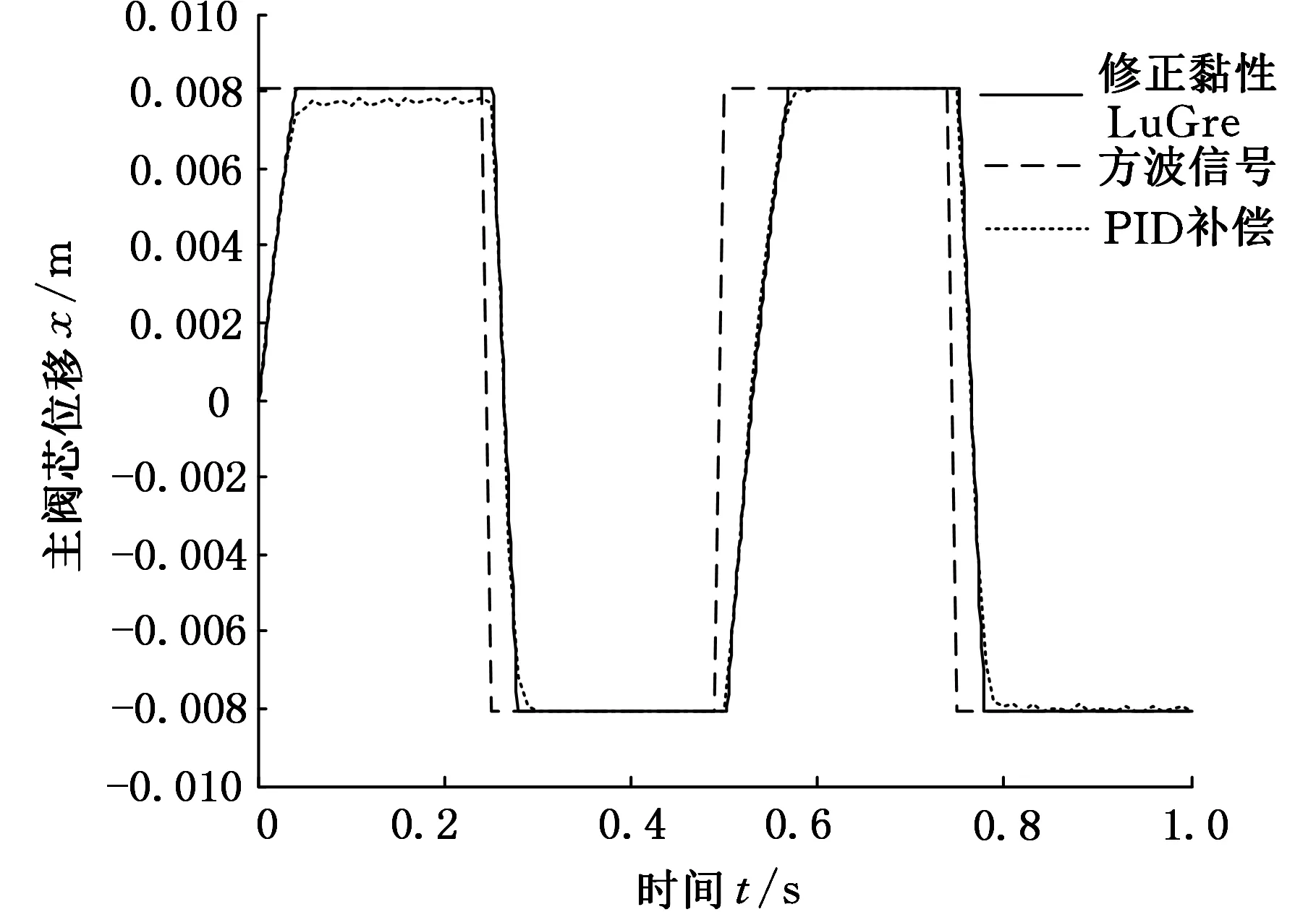
图15 位置跟踪曲线图Fig.15 Position tracking curves

通过图15位置跟踪曲线可以看出，基于修正黏性摩擦LuGre模型补偿与PID控制相比较，修正黏性摩擦LuGre模型能有效地抑制稳态极限环振荡，缩短响应时间，减小主阀芯位移误差。说明修正LuGre黏性摩擦模型能较好地补偿摩擦对阀位置跟踪特性的影响。

4 结论

(1)通过多路阀实验测试平台所测得的比例多路阀压力、流量、阀芯位移等数据，计算获得主阀芯摩擦力、速度数据。基于修正黏性摩擦LuGre模型辨识出摩擦力与速度的关系曲线，相比于LuGre模型，在Stribeck效应速度处拟合效果好，并且能够拟合出较高速度阶段摩擦力随速度增大其增长趋势减缓的特性。

(2)设计了基于修正黏性摩擦LuGre模型摩擦补偿控制器，运用AMESim和Simulink进行了摩擦补偿联合仿真。通过与PID常规控制策略相比较，基于修正黏性摩擦LuGre模型状态观测器的摩擦补偿方法能有效地减小摩擦对比例多路阀性能的影响，为比例阀的设计改进及工程应用提供参考。

[1] 向红标，谭文斌，李醒飞，等．基于LuGre模型的自适应摩擦补偿[J]．机械工程学报，2012，48(17)：70-74. XIANG Hongbiao, TAN Wenbin, LI Xingfei, et al. Adaptive Friction Compensation Based on LuGre Model[J]. Journal of Mechanical Engineering, 2012,48(17):70-74.

[2] AMIRANTE R, DISTASO E, TAMBURRANO P. Experimental and Numerical Analysis of Cavitation in Hydraulic Proportional Directional Valves[J]. Energy Conversion and Management, 2014,87：208-219.

[3] SAHA A, WAHI P, WIERCIGROCH M, et al. A Modified LuGre Friction Model for an Accurate Prediction of Friction Force in the Pure Sliding Regime[J/OL]. International Journal of Non-linear Mechanics. [2015-12-28]. http:// dx.doi.org/10.1016/j.ijnonlinmec.2015.08.013.

[4] 丁千，翟红梅．机械系统摩擦动力学研究进展[J]．力学进展，2013，43(1)：112-131. DING Qian, ZHAI Hongmei. The Advance in Researches of Friction Dynamics in Mechanics System[J]. Advances in Mechanics,2013,43(1):112-131.

[5] KHAYATI K, BIGRAS P, DESSAINT L A. LuGre Model-based Friction Compensation and Positioning Control for a Pneumatic Actuator Using Multi-objective Output-feedback Control via LMI Optimization[J]. Mechatronics,2009,19(4):535-547.

[6] NASER M F M, IKHOUANE F. Hysteresis Loop of the LuGre Model[J]. Automatica,2015,59:48-53.

[7] 郭彦青，付永领，张朋．一种新型LuGre摩擦模型参数辨识方法[J]．机床与液压，2015，43(1)：150-152. GUO Yanqing, FU Yongling, ZHANG Peng. A Novel Parameters Identification Method for LuGre Friction Model[J]. Machine Tool & Hydraulics,2015,43(1):150-152.

[8] RUDERMAN M. Presliding Hysteresis Damping of LuGre and Maxwell-slip Friction Models[J]. Mechatronics,2015,30:225-230.

[9] 刘柏希，刘宏昭．基于LuGre摩擦模型的有杆抽油系统动态特性分析[J]．中国机械工程，2009，20(18)：2236-2240. LIU Baixi, LIU Hongzhao. Analysis for Dynamic Characteristics of the Suckerrod Pumping System Based on LuGre Friction Model[J]. China Mechanical Engineering,2009,20(18):2236-2240.

[10] 周金柱，段宝岩，黄进．LuGre摩擦模型对伺服系统的影响与补偿[J]．控制理论与应用，2009，25(6)：990-994. ZHOU Jinzhu, DUAN Baoyan, HUANG Jin. Effect and Compensation for Servo Systems Using LuGre Friction Model[J]. Control Theory & Applications,2009,25(6):990-994.

[11] 刘柏希，姚昊雄，聂松辉．基于区间分析的LuGre摩擦模型参数辨识方法[J]．中国机械工程，2013，24(19)：2647-2651. LIU Baixi, YAO Haoxiong, NIE Songhui. Parameter Identification of LuGre Frition Model Based on Interval Analysis[J]. China Mechanical Enginee-ring,2013,24(19):2647-2651.

[12] 王瑞娟，梅志千，李向国，等．机电伺服系统非线性摩擦自适应补偿的研究[J]．中国电机工程学报，2012，32(36)：124-129. WANG Ruijuan, MEI Zhiqian, LI Xiangguo, et al. Research on Adaptive Nonlinear Friction Compensation of Mechatronic Servo Systems[J]. Proceedings of the CSEE,2012,32(36):124-129.

[13] 谭文斌，李醒飞，向红标，等．修正黏性摩擦的LuGre模型的摩擦补偿[J]．天津大学学报，2012，45(9)：825-828. TAN Wenbin, LI Xingfei, XIANG Hongbiao, et al. Friction Compensation Based on LuGre Model with Modified Viscous Friction[J]. Journal of Tianjin University,2012,45(9):825-828.

[14] PIATKOWSKI T. Dahl and LuGre Dynamic Friction Models—The Analysis of Selected Properties[J]. Mechanism and Machine Theory,2014,73(2):91-100.

[15] 张剑. 含摩擦伺服系统的建模与控制研究[D]．合肥：中国科学技术大学，2011. ZHANG Jian. Modeling and Control of Servo System with Friction[D]. Hefei: University of Science and Technology of China, 2011.

[16] ZHANG Z, LI Z, ZHOU Q, et al. Application in Prestiction Friction Compensation for Angular Velocity Loop of Inertially Stabilized Platforms[J]. Chinese Journal of Aeronautics,2014,27(3):655-662.

(编辑 袁兴玲)

Friction Compensation of Proportional Multi-way Valve Based on Modified Viscous Friction LuGre Model

CHEN Dongning1,2LIU Yidan1,2YAO Chengyu3JIANG Donglin1,2WANG Kexun1,2

1.Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control,Yanshan University, Qinhuangdao, Hebei, 066004 2. Key Laboratory of Advanced Forging & Stamping Technology and Science(Yanshan University),Ministry of Education of China, Qinhuangdao, Hebei, 066004 3. Key Laboratory of Industrial Computer Control Engineering of Hebei Province, Yanshan University,Qinhuangdao, Hebei, 066004

To decrease the influences of friction on the proportional multi-way valves, the methods of friction characteristic analysis, parameter identification and friction compensation of proportional multi-way valves were proposed based on modified viscous friction LuGre model. The friction data were indirectly obtained through the experimental tests. The static and dynamic parameters of modified viscous friction LuGre model were identified by data fitting. The friction state observer of modified viscous friction LuGre model was designed by use of the identified parameters, and the output of state observer was fed back to the input port of control model to reduce the adverse effect of friction on the proportional multi-way valve performances. Simulation results show that the location tracking accuracy of proportional multi-way valves may be improved by using the friction compensation with identification parameter method based on modified viscous friction LuGre model.

proportional multi-way valve; friction compensation; LuGre model; viscous friction; parameter identification

2016-03-21

国家自然科学基金资助项目(51675460，51405426)；河北省自然科学基金资助项目(E2016203306)

TH137.52；TH117.1

10.3969/j.issn.1004-132X.2017.01.011

陈东宁，女，1978年生。燕山大学机械工程学院副教授、电气工程学院博士后研究人员。主要研究方向为系统可靠性、故障诊断及智能优化。获国家科技进步二等奖1项。发表论文40余篇。E-mail:dnchen@ysu.edu.cn。刘一丹，女，1992年生。燕山大学机械工程学院硕士研究生。姚成玉，男，1975年生。燕山大学电气工程学院教授、博士后研究人员。蒋栋林，男，1985年生。燕山大学机械工程学院硕士研究生。王可勋，男，1988年生。燕山大学机械工程学院硕士研究生。