基于单次料层冲击破碎质量模型的球磨选择函数
2017-02-10毛亚郎计时鸣单继宏金晓航浙江工业大学机械工程学院杭州30042浙江工业大学海洋研究院杭州3004
毛亚郎 孙 毅,2 计时鸣 单继宏 金晓航.浙江工业大学机械工程学院,杭州,30042.浙江工业大学海洋研究院,杭州,3004
基于单次料层冲击破碎质量模型的球磨选择函数
毛亚郎1孙 毅1,2计时鸣1单继宏1金晓航1
1.浙江工业大学机械工程学院,杭州,3100142.浙江工业大学海洋研究院,杭州,310014
为提高球磨破碎效率,以及构建球磨装置的颗粒破碎过程模型,开展了基于单次料层冲击破碎质量模型的球磨选择函数研究。根据料层夹持形态与落球冲击试验,将料层破碎分为低冲击能下的未完全破碎和高冲击能量下的完全破碎两种状态。分析了单位质量能耗特性和细颗粒对夹持破碎质量的影响,分别建立了两种破碎状态下的料层冲击破碎质量模型。结合冲击能量谱,构建了基于单次料层冲击破碎质量模型的球磨选择函数,将介质球径、颗粒特性等影响球磨破碎效率的参数纳入到选择函数中。
料层夹持形态;冲击破碎质量;选择函数;球磨
0 引言
在矿物、水泥、陶瓷、颜料等大规模粉体加工中,球磨机、振动磨、搅拌磨等球磨装置应用广泛[1]。球磨破碎过程影响因素多、能耗高、节能空间大。基于质量平衡原理的总体平衡模型是描述球磨破碎过程的重要数学模型[2],由表示破碎率(单位时间的破碎质量)的选择函数和表示粒度分布的破碎函数组成。但是总体平衡模型并未包含颗粒特性、介质球大小、填充率和转速率等这些影响球磨破碎效率的参数,实际应用时必须根据不同时间的分批间歇球磨结果来确定选择函数[3],该过程将球磨装置视为一个“黑盒”,不利于球磨过程的优化。因此,有必要构建包含球磨破碎参数的选择函数,使破碎过程描述由“黑盒”变为“白盒”,以改进球磨过程模型。
料层颗粒在冲击或挤压作用下产生破碎,通过筛分得到小于初始粒度破碎颗粒的质量,即破碎质量。AUSTIN[4]构建了考虑颗粒粒度、磨机直径、介质球径、填充率、转速率等影响因素的球磨破碎质量的经验公式。球磨效率与筒体内冲击破碎事件密切相关,CHO[5]用基于冲击能量的单次冲击破碎质量来表示选择函数。离散元方法(DEM)被用于球磨介质运动仿真,HÖFLER[6]将二维DEM仿真获得的冲击能量谱用于表示单次冲击破碎事件。DATTA等[7]建立了基于三维DEM冲击能量谱和多层料层破碎实验的选择函数。考虑到料层夹持形态对单次冲击破碎质量的影响,NOMURA等[8]建立了考虑夹持区域、夹持可能性的单层料层破碎的选择函数,BOURGEOIS[9]对单层料层中的单颗粒破碎模型进行了研究。TAVARES等[10]考虑了多次低能冲击和颗粒间的研磨对颗粒破碎的影响。TUZCU[11]完善了基于单颗粒破碎和冲击能量谱的选择函数。由此可见,球磨选择函数与料层夹持形态密切相关[6,12],有必要构建基于多层料层破碎的选择函数。本文根据料层夹持形态和DEM球磨冲击特性,开展单次料层冲击破碎试验,对破碎质量进行分析,构建基于料层夹持形态的单次冲击破碎质量模型,改进球磨选择函数。
1 单次料层冲击夹持破碎质量
落球冲击下料层的破碎质量与料层夹持形态密切相关,前期的研究发现料层夹持厚度约为2层,料层夹持范围由介质球大小、颗粒形态决定,较高的冲击速度(能量)能增加单次冲击的破碎质量,根据石英砂落球冲击试验建立了基于料层夹持形态模型的夹持破碎质量计算式[13]:
m=πρdD2sin2α/2
(1)
式中,ρ为颗粒堆积密度;d为颗粒粒径;D为介质球径;α为料层夹持角度,可由颗粒的安息角ψ计算得到,对于粒径1 mm左右的石英砂,α=ψ-23.61°。
根据夹持料层内颗粒是否全部破碎,把料层破碎状态分为未完全破碎和完全破碎。实际球磨破碎时,冲击能量大小不等,不能保证每次冲击都能使夹持范围内颗粒全部破碎,必须分别考虑低冲击能量和高冲击能量下的不同破碎特性。
1.1 低冲击能下的破碎质量
1.1.1 破碎质量与单位质量能耗
开展了不同落球高度下的石英砂料层冲击试验(实验1),实验方法和装置与文献[13]相同。其中钢球直径为25 mm,石英砂粒度为18~20目,初始料层厚度为3 mm,堆积密度为1.43 g/cm3。料层破碎质量随冲击高度的变化趋势如图1中的实线所示,可将料层破碎分为两个阶段:低冲击能量阶段(冲击高度H=20~150 mm)和高冲击能量阶段(H>150 mm)。低冲击能量阶段,被夹持颗粒未完全破碎,破碎质量随冲击高度(能量)快速增大;高冲击能量阶段,被夹持颗粒完全破碎,破碎质量随冲击高度(能量)缓慢增大,颗粒的破碎状态如图2所示。DATTA等[7]对石灰石料层的落球冲击试验也得到类似的结果。将曲线变化转折位置(H=150 mm)视为未完全破碎与完全破碎(低冲击能与高冲击能)的临界点,对应的冲击能量和破碎质量用E0和m0表示,m0可用夹持破碎质量式(1)表示,可见夹持破碎质量是划分高低冲击能量的依据。
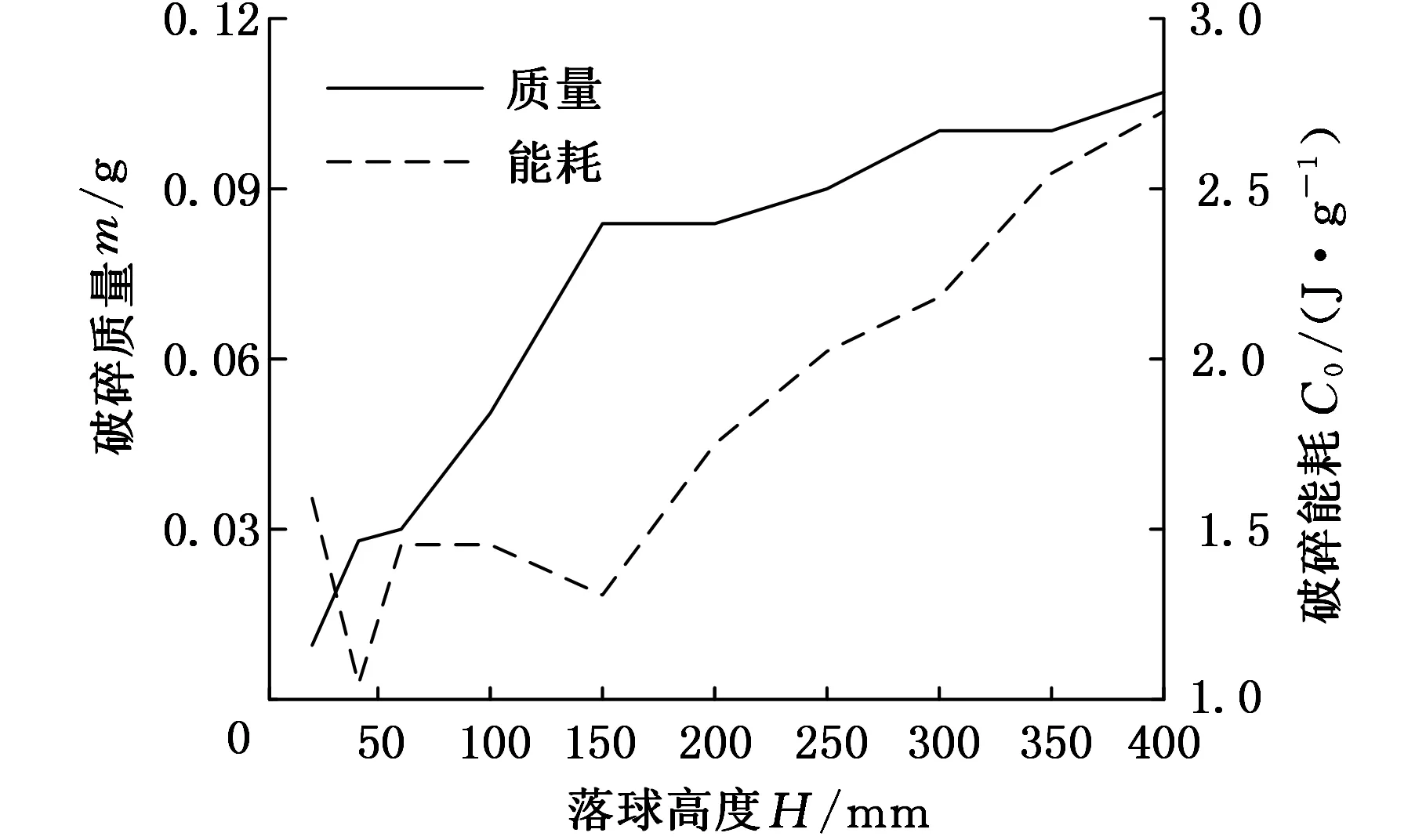
图1 不同冲击高度下破碎质量与破碎能耗Fig.1 Breakage mass and mass-specific breakage energy of quartz beds with different impact heights

图2 不同冲击高度下颗粒的破碎形态Fig.2 Shape of quartz fragments with different impact heights
实验1的单位质量能耗(冲击能量与破碎质量之比)随冲击高度的变化如图1中虚线所示,在未完全破碎阶段,单位破碎质量能耗基本相同,完全破碎阶段能耗显著增加,增加的能耗使破碎颗粒更细,颗粒破碎程度如图2所示。可见未完全破碎阶段的破碎质量与冲击能成正比,即
Ek/m=C0
(2)
式中,Ek为冲击能;C0为未完全破碎下的单位质量能耗。
1.1.2 颗粒粒度与单位质量能耗的关系
受颗粒内部缺陷、微裂纹分布的影响,颗粒单位质量能耗会随着颗粒粒度的减小而增大,与粒度大小成指数关系[14]。TAVARES等[15]根据不同材料不同粒度的单颗粒破碎试验,建立了单位质量能耗与颗粒粒径的关系式:
Em50=Em,∞[1+(d0/d)]φ
(3)
其中,Em50表示单颗粒在50%破碎概率下的单位质量能耗;参数Em,∞、d0和φ由单颗粒破碎试验数据拟合得到,其中石英砂的参数值分别为0.043 J/g,3.48 mm,1.61。低冲击能下,料层颗粒处于未完全破碎状态,与单颗粒破碎状态相似,将式(3)用于料层颗粒的未完全破碎阶段。但是未完全破碎阶段的单位质量能耗C0是根据所有破碎颗粒的质量进行计算的,不同于单颗粒50%破碎概率下的Em50。因此对式(3)的Em,∞进行修正,将18~20目石英砂料层破碎的C0≈1.45 J/g代入式(3)取代Em50,求得Em,∞的修正值为0.105 J/g,得不同粒度石英砂料层的单位破碎质量能耗为
C0=0.105[1+(3.48/d)]1.61
(4)
将式(4)计算得到的不同粒度下单位质量能耗与文献[15]石英砂单颗粒破碎实验结果进行比较发现,单颗粒的破碎概率在95%以上,计算结果与实验结果基本相符。
1.2 高冲击能下的破碎质量
1.2.1 完全破碎质量模型
通过式(1)可计算在冲击能量E0下料层夹持范围内颗粒的夹持破碎质量,但是实际破碎质量会随着冲击能量的增大而增大。为此开展了1层、2层和3层不同层数石英砂颗粒的落球冲击试验(实验2),分析破碎质量增大的原因。实验参数与实验1相同,实验结果如图3所示。由图3中料层数为1层和2层的破碎质量变化趋势可以发现,在完全破碎阶段冲击能量的增大对破碎质量影响很小,说明夹持范围基本未变,多层料层下增加的破碎质量并非来源于被夹持的1~2层颗粒。结合文献[13]的相同冲击高度、不同冲击能量下夹持料层的完全破碎质量相同的结论,进一步确认由于多层颗粒在被夹持前的剪切滑移导致了颗粒破碎质量的增大,冲击速度的增大加剧了该现象,使破碎质量随冲击能量的增大而增大。但是破碎质量的增大受料层本身的限制,冲击能量越大,相对增量越小,DATTA[14]用对数函数表示破碎质量与冲击能量的关系如下:
m=a1lnEk-b
(5)
式中,a1、b为函数系数。
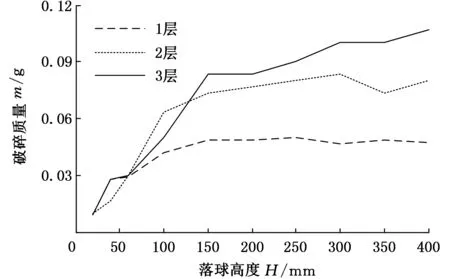
图3 料层厚度对破碎质量的影响Fig.3 Effect of the particle-beds Layer on breakage mass
根据冲击能量为E0时料层夹持破碎质量为m0,可得
(6)
可见冲击能量为Ek时,完全破碎质量包括两部分:夹持破碎质量和剪切滑移破碎质量。系数a1表示破碎质量随冲击能量增大的增量系数,它会随颗粒粒度增大而增大[14]。
1.2.2 细颗粒对夹持破碎质量的影响
在实际球磨过程中,颗粒粒度会越来越小,可能出现破碎过程中落球已与铁砧接触,料层难以进一步挤压的情况,如图4所示,而处于夹持区域内(α内)的外围颗粒并未有被夹持和破碎的现象(因外围料层厚度仍大于2层颗粒的堆叠厚度),导致实际破碎夹持范围小于理论值。
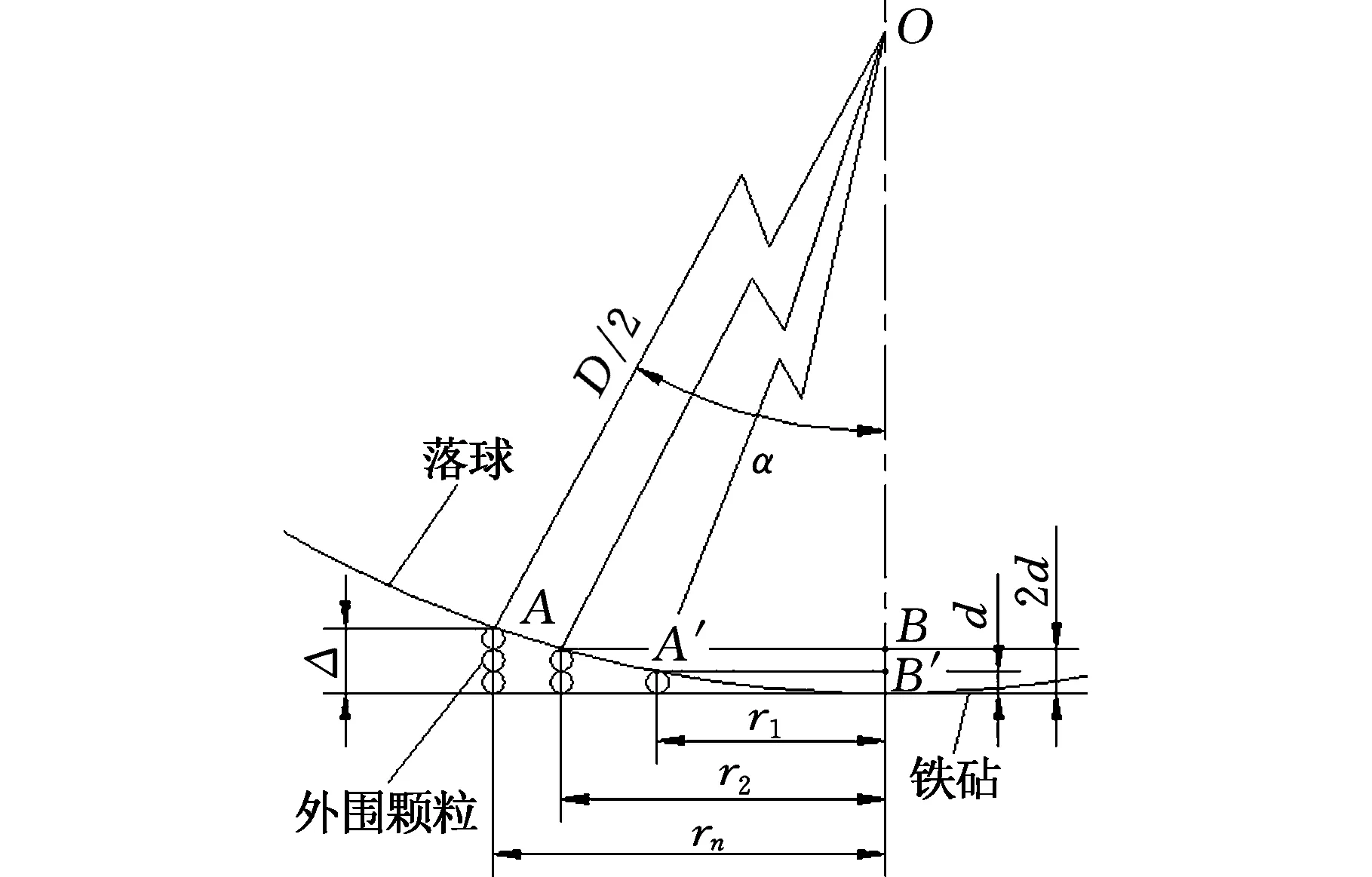
图4 细颗粒夹持状态Fig.4 Nipped configuration of fine particles
图4中的Δ表示落球已与铁砧接触时夹持区域边界处的球面与铁砧的高度差,其大小为
(7)
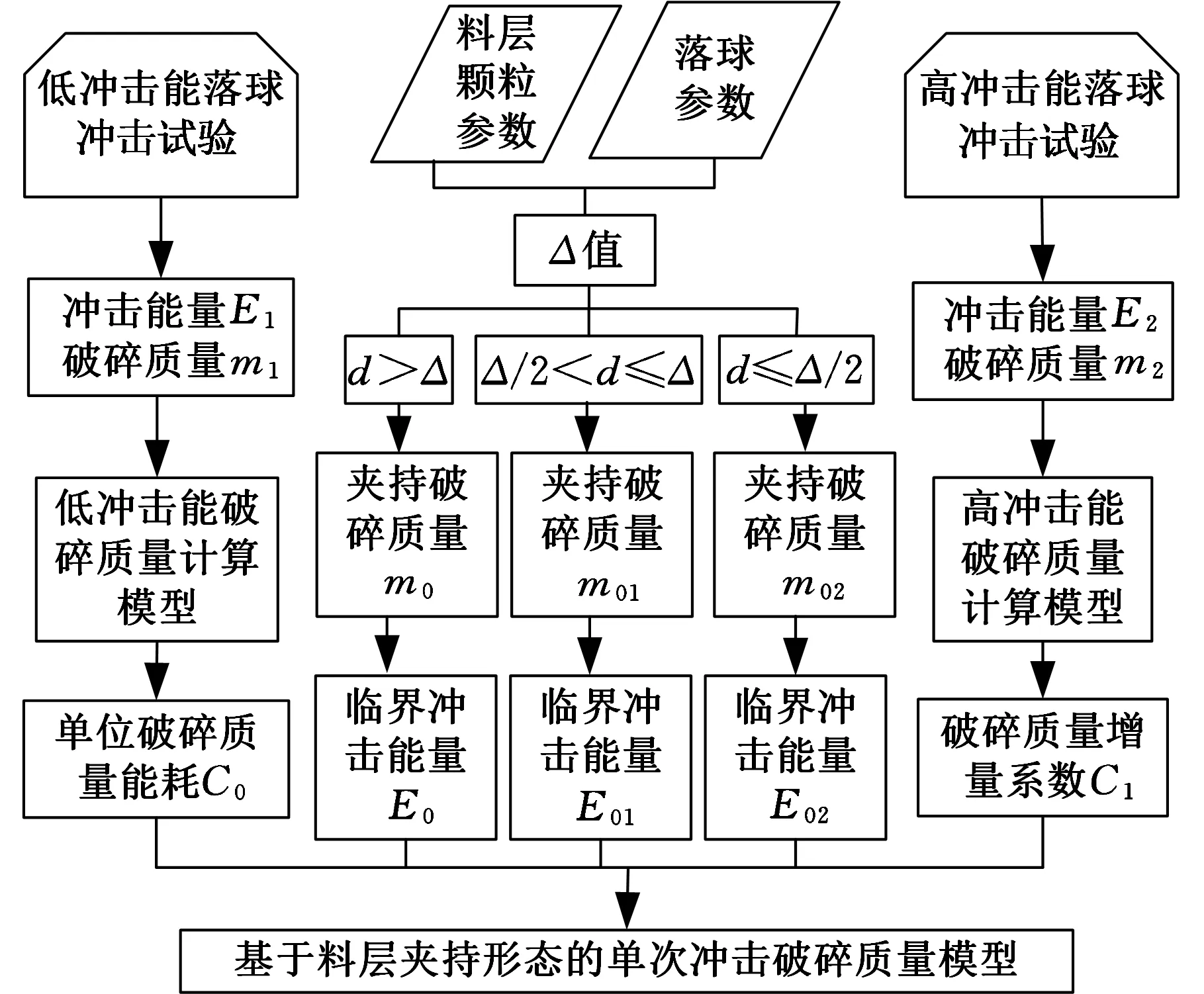
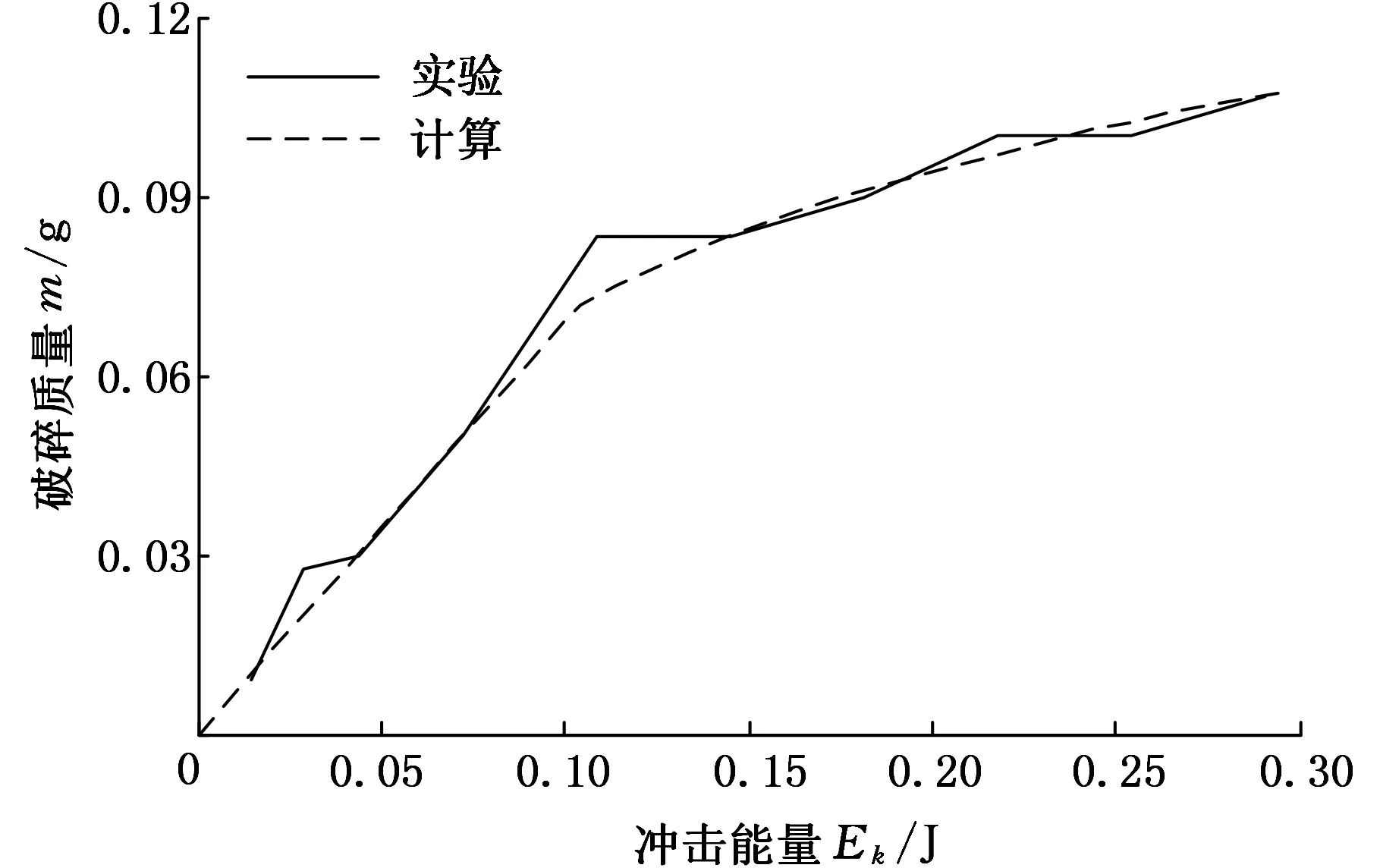
忽略落球与铁砧间残留破碎物以及冲击变形的影响,为确保理论夹持范围内所有颗粒被破碎,必须满足外围只有单个颗粒时也能受到落球挤压,即d>Δ。当Δ/2 当Δ/2 (8) 求得破碎质量m2=πρd2(D-d),加上上层颗粒的全部破碎质量得总夹持破碎质量: m01=πρd(D2sin2α/4+Dd-d2) (9) 当d≤Δ/2时,上层颗粒的实际夹持范围根据图4中的直角三角形OAB可得 (10) 下层颗粒的实际夹持范围计算与式(8)相同,两层颗粒夹持破碎质量为 m02=πρd2(3D-5d) (11) 将m01、m02代入式(2)可得相应的临界破碎能为E01、E02。 综上,可得单次料层冲击下的破碎质量模型为 (12) 式(12)中,当d>Δ时,E0j=E0,m0j=m0;当Δ≥d>Δ/2时,E0j=E01,m0j=m01;当d ≤Δ/2时,E0j=E02,m0j=m02。 构建破碎质量模型时,只要通过低冲击能和高冲击能下的两次落球冲击试验就能确定C0、E0和a1值,具体流程如图5所示。现以粒度为18~20目的石英砂落球冲击试验为例进行说明。将落球直径D=25 mm,石英砂料层参数ρ=1.43×10-3g/mm3、d=0.85 mm、α=14.19°代入式(1)得m0=0.072 g。根据落球高度为60 mm的低冲击能落球冲击试验获得E1、m1,代入式(2)求得单位质量能耗C0=1.45 J/g。将m0代入式(2)得E0=0.104 J。根据式(7)计算得Δ=0.38 mm,d>Δ。根据式(6)计算完全破碎质量。根据落球高度为400 mm的高冲击能落球冲击试验获得E2、m2,代入式(6)得a1=0.034 g。根据上述计算结果作出破碎质量随冲击能量的变化曲线,如图6中虚线所示,与实验数据(实线)比较,两者基本一致。 图5 破碎质量构建流程Fig.5 Procedure of breakage mass modeling 图6 料层破碎质量曲线Fig.6 Breakage mass of quartz beds 只有获得磨机内不同介质球冲击次数、冲击能量,才能通过累加单次冲击破碎质量构建磨机的选择函数。假设介质球提升时不发生滑动且呈圆周分布,NOMURA等[8]从理论上计算了球磨机内介质球的冲击数量和冲击能量。由于假设过于理想化,无法体现提升衬板、混合介质、摩擦因数等工况参数对球磨效率的影响,故理论计算与实际球磨差异较大。DEM是模拟球磨介质运动的有效工具[2],可获得不同球磨工况下的每次冲击的介质球径、能量等信息[16-17], DATTA等[7]建立了基于冲击能量谱的选择函数: (13) 式中,λk表示单位时间内冲击能量为Ek的冲击次数,通过DEM球磨机的介质运动仿真得到;mi,k为在冲击能量为Ek时粒级为i的颗粒的单次冲击破碎质量,通过对4层厚的料层落球冲击试验得到。 DATTA等[7]通过落球冲击试验数据拟合的方法建立了基于冲击能量的破碎质量模型,如式(5)所示。但是实际料层夹持破碎质量与介质球径、颗粒形态、破碎状态密切相关,该质量模型过于简化和经验化。 参照式(13)的选择函数,将基于料层夹持形态的单次冲击破碎质量模型式(12)取代mi,k,构建包含破碎质量影响因素的选择函数: (14) 其中,C0,i表示粒度为di颗粒的单位质量能耗,由式(4)计算;E0j,i,n、m0j,i,n分别表示粒度为di的颗粒在直径为Dn的落球冲击下夹持料层全部破碎所需的临界冲击能量和夹持破碎质量,当d>Δ时,E0j,i,n= E0,i,n,m0j,i,n= m0,i,n;当Δ≥d>Δ/2时,E0j,i,n= E01,i,n,m0j,i,n= m01,i,n;当d≤Δ/2时,E0j,i,n=E02,i,n,m0j,i,n= m02,i,n。λk表示单位时间内能量等级为k级的冲击次数(其中Ek≤E0j,i,n);λk,n表示单位时间球径为Dn能量等级为k级的冲击次数(其中Ek>E0j,i,n);冲击的能量等级Ek、球径Dn及其次数λ由DEM介质运动仿真获得。 利用DEM软件对磨机进行介质运动仿真以获得冲击特征数据,结合式(14)和颗粒冲击破碎函数,即可通过总体平衡方程计算球磨产品粒度分布,用于确定和优化球磨参数。 (1)提出了一种根据落球冲击下料层夹持形态及其破碎质量模型构建球磨破碎过程选择函数的方法,将介质球、颗粒特性等影响球磨效率的参数包含到选择函数中。 (2)夹持料层未完全破碎时,颗粒破碎质量与冲击能量成正比,单位质量能耗与颗粒粒径成指数关系。 (3)夹持料层完全破碎时,颗粒破碎质量包含完全破碎质量和高冲击能量导致的破碎增量两部分,分析了细颗粒对夹持料层完全破碎质量的影响。 (4)以石英砂颗粒为例说明了通过高低冲击能的落球冲击试验构建单次冲击破碎质量模型的过程,过程简单便捷。 [1] 陶珍东,郑少华.粉体工程与设备[M]//2版.北京:化学工业出版社,2010. TAO Zhendong,ZHENG Shaohua.Powder Technology and Equipment[M]//2nd.Beijing: Chemical Industry Press,2010. [2] 威尔斯 B A,纳皮尔马恩 T.矿物加工技术[M]//7版.北京:冶金工业出版社,2011. WILLS B A,NAPIER-MUNN T.Mineral Processing Technology[M]//7th. Beijing:Metallurgical Industry Press,2010. [3] 王泽红,陈晓龙,袁致涛,等.选矿数学模型[M].北京:冶金工业出版社,2015. WANG Zhehong,CHEN Xiaolong,YUAN Zhitao,et al.Mathematical Model on Mineral Processing [M]. Beijing:Metallurgical Industry Press,2015. [4] AUSTIN L G.Understanding Ball Mill Sizing[J].Industrial & Engineering Chemistry Process Design & Development,1973,12(2):121-129. [5] CHO K. Breakage Mechanisms in Size Reduction[D].Salt Lake City:Univ. of Utah,1990. [6] HÖFLER A. Fundamental Breakage Studies of Mineral Particles with an Ultrafast Load Cell Device[D].Salt Lake City:Univ. of Utah,1990. [7] DATTA A,RAJAMANI R K.A Direct Approach of Modeling Batch Grinding in Ball Mills Using Population Balance Principles and Impact Energy Distribution[J].International Journal of Mineral Processing,2002,64(4):181-200. [8] NOMURA S,HOSODA K,TANAKA T.An Analysis of the Selection Function for Mills Using Balls as Grinding Media[J].Powder Technology,1991,68(1):1-12. [9] BOURGEOIS F S.Single Particle Fracture as Basis for Microscale Modeling of Comminution Processes[D].Salt Lake City:Univ. of Utah,1993. [10] TAVARES L M,CARVALHO R M.Modeling Breakage Rates of Coarse Particles in Ball Mills[J].Minerals Engineering,2009,22:650-659. [11] TUZCU E T.An Approach for the Modeling of Batch Grinding with Single Particle Fracture Studies and Impact Energy Spectra[D].Salt Lake City:Univ. of Utah,2010. [12] 毛亚郎,孙毅,计时鸣,等. 介质球间非限制料层夹持形态研究[J].中国机械工程,2014,25(23):3212-3215. MAO Yalang,SUN Yi,JI Shiming,et al.Nipped Configuration of Unconfined Particle Beds Between Media Balls[J].China Mechanical Engineering,2014,25(23):3212-3215. [13] 毛亚郎,孙毅,计时鸣,等.落球冲击破碎下的非限制料层夹持形态[J].中国机械工程,2016,27(2):168-172. MAO Yalang,SUN Yi,JI Shiming,et al.Nipped Configuration of Unconfined Particle Beds under Falling Ball Impact Test[J].China Mechanical Engineering,2016,27(2):168-172. [14] DATTA A. A Model of Batch Grinding with Impact Energy Spectra[D].Salt Lake City:Univ. of Utah,1999. [15] TAVARES L M,King R P.Single-particle Fracture under Impact Loading[J].International Journal of Mineral Processing,1998,54(1):1-28.[16] TUZCU E T,RAJAMANI R K.Modeling Breakage Rates in Mills with Impact Energy Spectra and Ultra Fast Load Cell Data[J]. Minerals Engineering,2011,24(3/4):252-260. [17] CLEARY P W,MORRISON R.Comminution Mechanisms,Particle Shape Evolution and Collis-ion Energy Partitioning in Tumbling Mills[J].Minerals Engineering,2016,86:75-95. (编辑 袁兴玲) Selection Function Based on Single-impact Breakage Mass Model of Particle Beds in Ball Mills MAO Yalang1SUN Yi1,2JI Shiming1SHAN Jihong1JIN Xiaohang1 1.College of Mechanical Engineering,Zhejiang University of Technology,Hangzhou,310014 2.Institute of Ocean Research,Zhejiang University of Technology,Hangzhou,310014 In order to establish the particle comminution process model and improve the grinding efficiencies in ball mills, the studies of the selection function were carried out based on the single-impact breakage mass model. According to the nipped configurations and the falling ball impact tests, the particle-bed breakage was divided into the incomplete breakage in low impact energy and the complete breakage in high impact energy. The energy of mass specific fracture energy and the effects of fine particles on nipped breakage mass were analyzed. The models of the single-impact breakage mass under two broken states were built respectively. The selection function, which included the breakage influence factors such as media diameter, particle size and particle shape of ball mill, was set up based on the impact energy spectrum and the single-impact breakage mass model. nipped configuration of particle bed; impact breakage mass; selection function; ball mill 2016-03-02 国家自然科学基金资助项目(51675484,51275474,51505424);浙江省自然科学基金资助项目(LZ12E05002,LY15E050019) TD921 10.3969/j.issn.1004-132X.2017.01.001 毛亚郎,男,1978年生。浙江工业大学机械工程学院博士研究生、讲师。主要研究方向为粉磨机械与装备。发表论文4篇。孙 毅(通信作者),男,1966年生。浙江工业大学机械工程学院教授、博士研究生导师。E-mail:sunyi@zjut.edu.cn。计时鸣,男,1957年生。浙江工业大学机械工程学院教授、博士研究生导师。单继宏,男,1970年生。浙江工业大学机械工程学院副教授。金晓航,男,1981年生。浙江工业大学机械工程学院副教授。2 破碎质量模型实例
3 基于冲击能量谱和单次冲击破碎的球磨选择函数
4 结论
