柔性对涡街中细丝运动状态的影响

刘亮，何国毅，何心怡，王琦

（南昌航空大学 飞行器工程学院，南昌 330063）

0 引 言

在自然界中，游动或飞行动物通过鳍、翅膀、尾部、躯干等结构的摆动来获得推力、升力是非常普遍的现象。在摆动过程中，动物的身体往往会发生比较大的变形，其中柔性起着至关重要的作用。实验研究表明，柔性可以提高推进性能。对游动或飞行过程中动物身体或者翅膀柔性的研究，不仅有助于了解运动机理，也能为飞行器和自主水下航行器的设计提供参考。

近年来，考虑到生物体柔性的特点，同时为了摒除其他因素的影响，一些研究者单独研究柔性对推进性能的影响，将翅膀、鳍、鱼类的尾部以及躯干等柔性结构，简化成柔性扑翼、细丝等模型。D. Iverson 等通过对扑翼的弦向柔性进行研究，发现和刚性扑翼相比，柔性扑翼可以提高推力和运动效率；张云飞等的研究表明，展向柔性的引入改变了扑翼有效攻角沿展向的分布，并且适当的展向柔性可以减小阻力系数，但是过大的展向柔性却会增加阻力系数；Z. Peng 等通过数值模拟，发现当细丝的柔性从头端到尾端逐渐减小时，其推力要高于柔性不变的细丝；N. L.Kelsey 等发现，当水翼的前1/3 部分的柔性比较小，后2/3 部分的柔性比较大时，推进效率是最高的。对于鱼类来说，虽然有很多因素（材质，外形，流体之间的相互作用，驱动方式）影响推力的产生和游动效率，但是被动不均匀柔性是影响推力和效率的主要变量。

需要指出的是，在大部分对柔性的研究中，只探究了柔性对推力、运动效率以及推进速度的影响，关于柔性对运动状态以及其他方面影响的研究还比较少。Zhu X 等通过自推进柔性细丝模型，探究了柔性对尾涡对称性的影响：增加细丝的柔性，会导致细丝头端攻角减小，使得头端涡量降低，同时也会增加尾端的拍打速度，导致尾端涡量的增加，这两种相反的作用相互影响，最终决定尾涡的对称性。通过对串联布置在均匀来流中的两根头端固定细丝进行数值模拟研究（细丝的头端在水平方向和竖直方向上都是固定不动的，其他部分是自由的），Zhu L D发现，在其他实验条件都相同的情况下，细丝柔性较大时，细丝能处于摆动状态，但是当细丝柔性较小时，细丝几乎处于静止状态。

鸟类在长途迁徙的过程中经常能保持一定的队形规律飞行，后面的个体通常位于前面个体的涡街中，并且当鸟群保持“V”字形队飞行时，位于侧后方的个体能够节约能量。为了探究其中的流体力学机理，研究者提出了涡街中的细丝模型。Lin Xingjian 等通过对扑翼尾迹中的细丝进行研究，发现当细丝在涡街中做绕核运动（细丝总是绕着涡核运动，并不会与涡核相撞，类似于障碍滑雪）时，相比于当细丝在涡街一侧运动，细丝的阻力明显减小；王思莹等通过对比柔性细丝在卡门涡街和自由来流中的运动，发现在卡门涡街中，细丝的摆动频率和卡门涡街脱泄的频率相同，并且受推力作用，但是在自由来流中，细丝受阻力作用。

在上述研究中，无论是自推进柔性细丝模型还是头端固定细丝模型，细丝在垂直于前进方向上的运动都是受到限制的，在竖直方向上的流—固耦合作用可能会被忽略，无法充分探究柔性对细丝运动状态的影响。

本文在侧向完全自由的柔性细丝模型基础上，给出三种细丝柔性分布模式，均匀柔性、连续变柔性和分段柔性分布；并应用浸入边界法（Im⁃mersed Boundary Method），通过数值模拟分析柔性变化对细丝运动状态的影响。

1 物理模型和数值方法

1.1 物理模型

本文物理模型中左边是刚性扑翼，右边是柔性细丝，二者均置于从左向右的二维不可压缩均匀来流中（如图1 所示）。其中，、分别为扑翼弦长和头端直径；为扑翼最大摆角；为细丝长度；为初始来流速度；为细丝头端和扑翼尾端的距离。

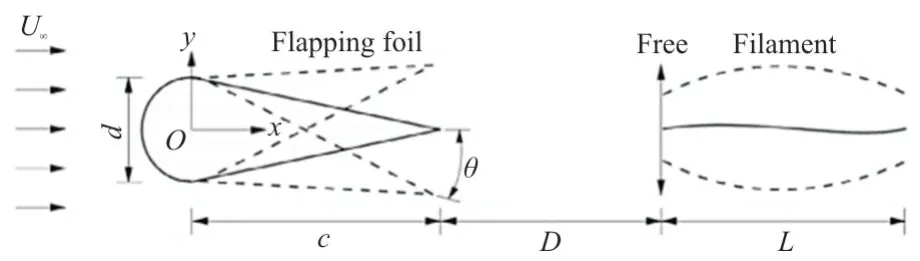
图1 位于扑翼尾迹中的侧向自由细丝模型示意图Fig.1 Diagrammatic sketch of the physical model

刚性扑翼绕着头端半圆中心摆动，摆动方程为

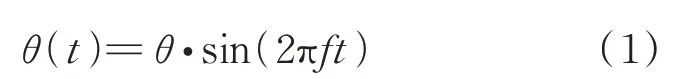
式中：（）为扑翼的摆角，是时间的函数；为扑翼最大摆动角度；为摆动频率。

通过给定参数和的不同取值，扑翼可以产生不同的尾迹，包括卡门涡街和反卡门涡街。细丝的头端在水平方向上是固定的，在垂直方向上是自由的，细丝其他部分在水平方向和垂直方向上都是不受限制的。在扑翼产生的尾迹稳定之后，沿来流方向（=0），细丝被水平放置在涡街中。在周围流体的作用下，细丝被动摆动。

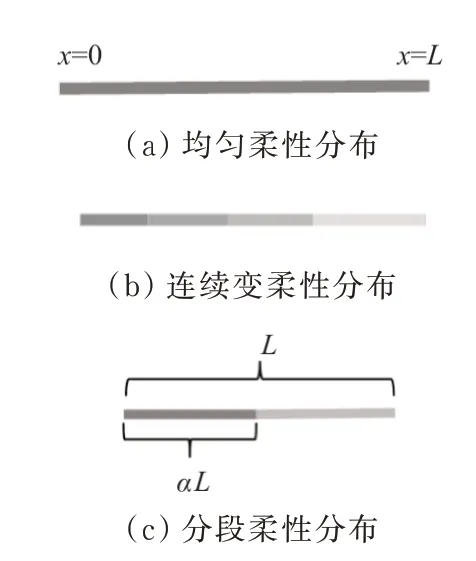
图2 细丝的三种柔性分布模式示意图Fig.2 Three flexible distribution modes of the filament

1.2 数值方法

流—固系统的控制方程为

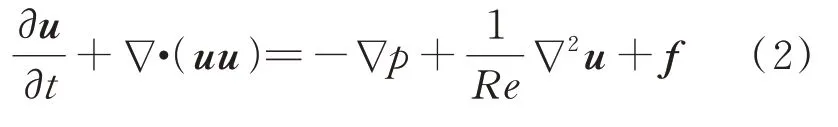
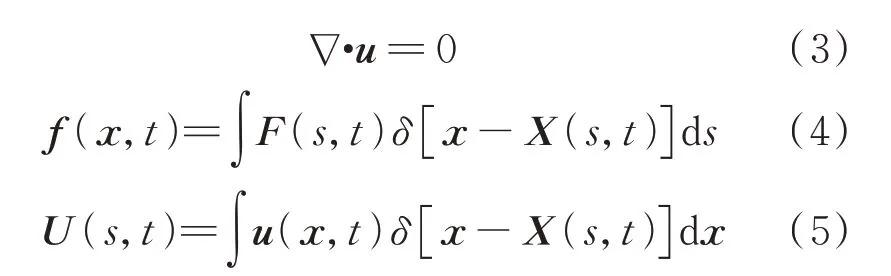
式中：，和（）分别为流体的速度，压强和细丝的位置坐标；和分别为欧拉力密度和拉格朗日力密度，表示流体和固体间的相互作用；为拉格朗日坐标；为时间。

式（2）～式（5）均是无量纲形式，是通过细丝长度和初始来流速度进行无量纲化的（=1.0，=1.0）。

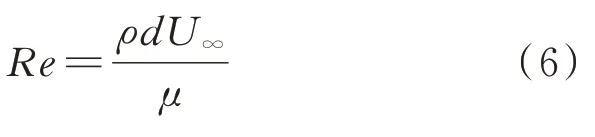
式中：为雷诺数，=255；为流体密度；为扑翼头端直径；为动力黏度。

本文使用到的其他主要无量纲参数定义为

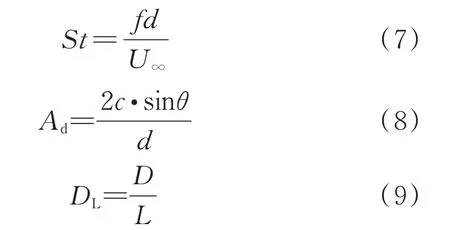
式中：为基于扑翼扑动频率的斯特劳哈尔数；为扑翼摆动的的振幅；为细丝和扑翼之间的水平距离。

此扑翼细丝模型存在两种浸入边界，一种是扑翼的刚性边界，另外一种是细丝的柔性边界，因此，浸入边界和流体之间的相互作用力由两部分组成，如式（10）所示。

式中：（，）为流体和浸入边界之间的相互作用力；（，）为流体和刚性扑翼之间的相互作用力；（，）为流体和柔性细丝之间的相互作用力。

计算周围流体和细丝之间相互作用力的方程如下：

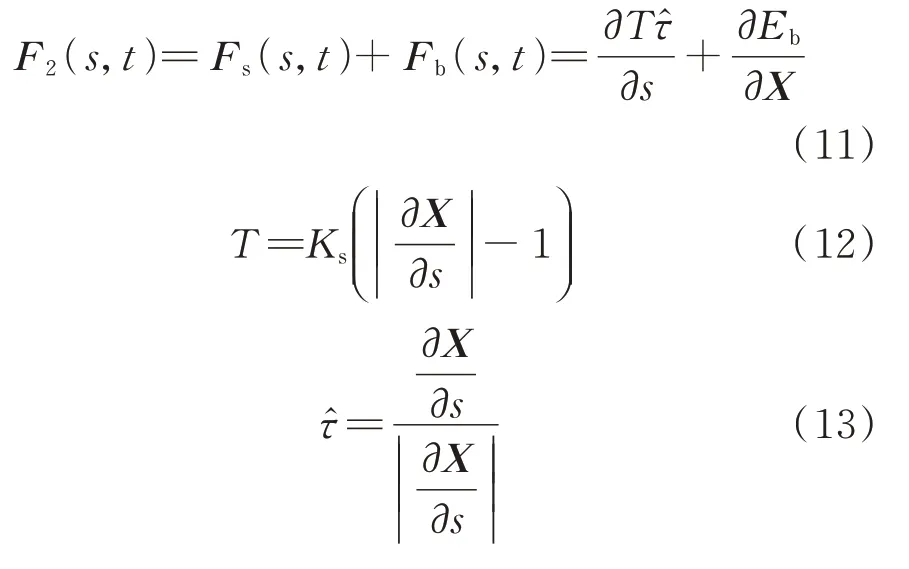
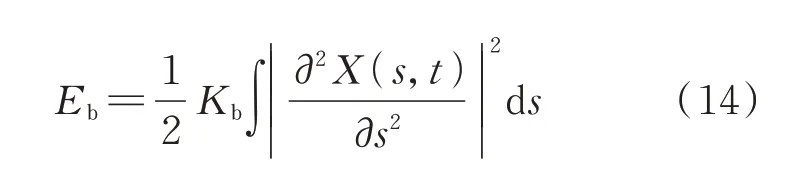
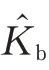
扑翼和流体之间的相互作用，通过以下方程计算：

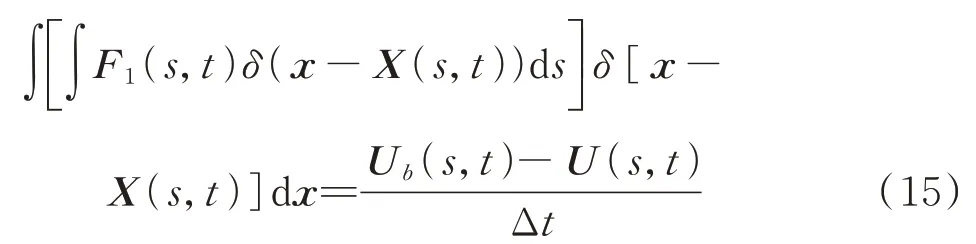
式中：U(，)为扑翼的实际速度；(，)为扑翼的浸入边界速度（根据流体速度估算得到）。

对于固体结构，无滑移边界条件施加在柔性细丝和刚性扑翼表面。施加在细丝头端（=0）的边界条件为

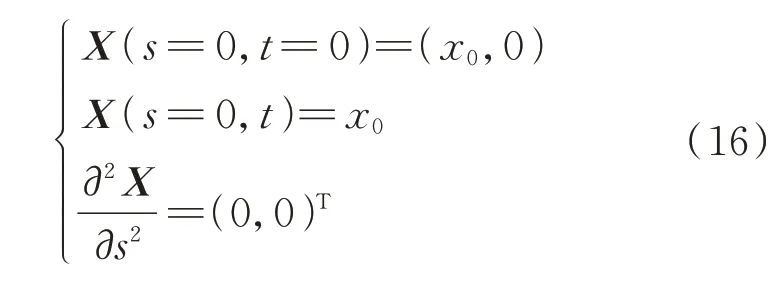
施加在细丝自由端（=）的边界条件为

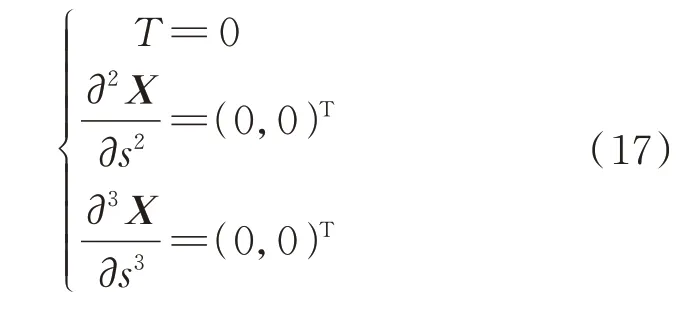
采用浸入边界法对扑翼细丝模型进行数值模拟计算，计算区域为矩形，尺寸为-5＜＜20，-8＜＜8。本文所使用的计算网格参考于课题组前期的工作，计算网格由280×160 个空间网点组成，网格宽度为Δ=Δ=0.025，时间步长为d=0.002。通过模拟在均匀流中圆柱体的振荡以及位于圆柱绕流中细丝的运动，得到本文所使用的求解程序验证是准确的。

2 计算结果与分析

2.1 细丝运动状态计算结果

通过改变扑翼的摆动频率和最大摆角，扑翼可以产生不同的尾迹，包括卡门涡街和反卡门涡街。在扑翼产生的尾迹稳定之后，细丝才被放入扑翼的尾迹中。通过对比6 组数据（如表1 所示），分别在卡门涡街和反卡门涡街中，探究柔性对细丝运动模式的影响。

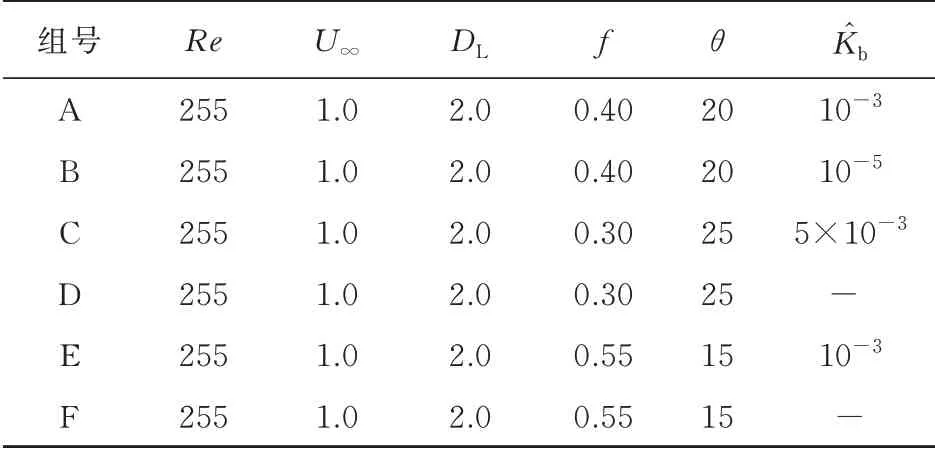
表1 对比实验中的物理参数设置Table 1 Physical parameter settings in the comparative experiment

在A、B、C、D 四组对比实验中，扑翼产生的尾迹为卡门涡街。A、B 两组实验除了细丝柔性不同，其他参数都是相同的，在这两组实验中，细丝的柔性都是均匀的，但是B 组中的细丝柔性更大。在A 组实验中，细丝做绕核运动，即细丝总是在相邻涡核之间来回穿梭摆动，逆时针方向旋转的漩涡（正涡）总是会从细丝的下侧（-方向）通过，而顺时针旋转的漩涡（负涡）总是会从细丝的上侧（+方向）通过，细丝做绕核运动时，一个周期内四个时刻的涡量云图如图3 所示。

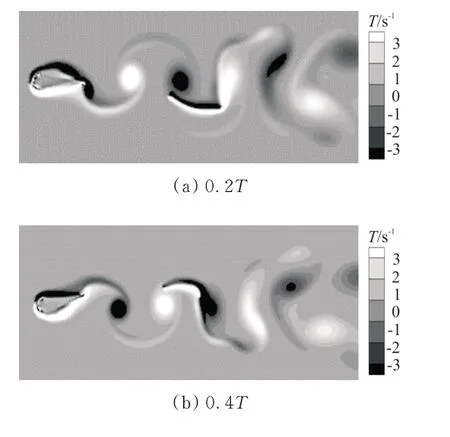
图3 柔性细丝做绕核运动时，一个周期内的四个不同时刻的涡量云图（St=0.12，Ad=2.1）Fig.3 The instantaneous vorticity contours and filament shapes within a complete swing cycle（St=0.12，Ad=2.1）

在A 组实验中，细丝在涡核间做绕核运动的结果如图4 所示。在B 组实验中，细丝的运动模式和A 完全不同，细丝在涡街一侧运动，即细丝总是保持在涡街外侧摆动，不会返回到涡街中间的位置，正涡和负涡都在细丝的相同一侧（上侧或者下侧）。细丝在涡街一侧运动时，一个周期内四个时刻的涡量云图如图5 所示。

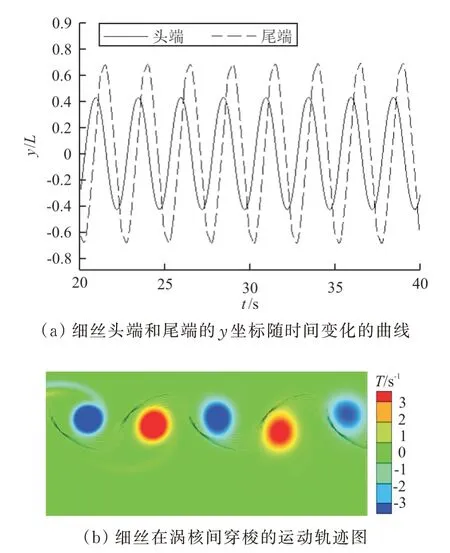
图4 A 组实验结果结果Fig.4 Results of group A

图5 柔性细丝在涡街一侧运动时，一个周期内的四个不同时刻的涡量云图（St=0.22，Ad=2.1）Fig.5 The instantaneous vorticity contours and filament shapes within a complete swing cycle（St=0.22，Ad=2.1）

在B 组实验中，细丝在涡街一侧运动的结果如图6 所示。

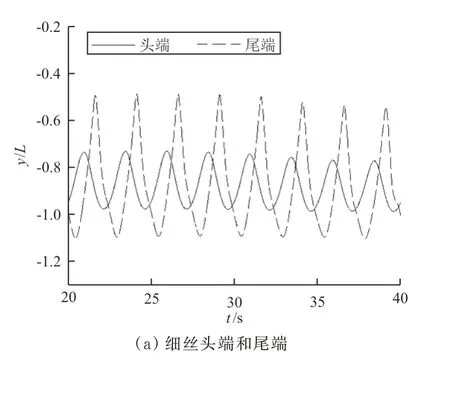
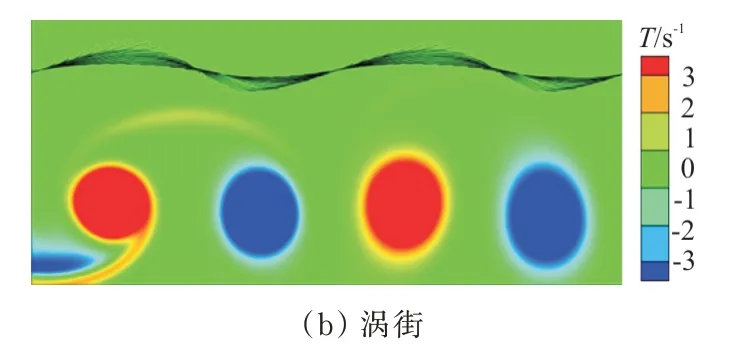
图6 B 组实验结果Fig.6 Results of group B

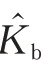
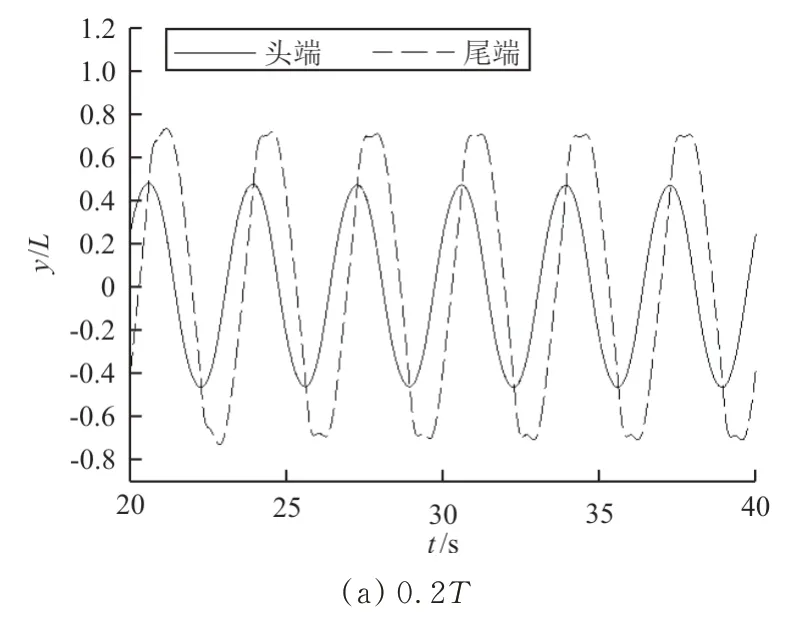
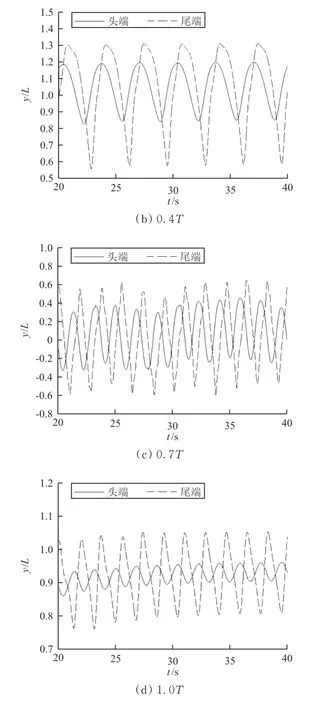
图7 细丝头端和尾端的y 坐标随时间变化的曲线Fig.7 The curve of the y coordinate of the filament changing with time

2.2 细丝运动状态随柔性变化的规律

由于细丝是被静止地放入涡街中，在竖直方向上，没有受到除流场力以外的其他任何力的作用。细丝在竖直方向的摆动（向上摆动或者向下摆动）是因为受到扑翼扑动产生的涡对诱导速度在方 向 的 分 量V的 作 用，其 中，V=(/2π)sin，为涡环量，为两相邻涡核之间的距离，为诱导速度和水平线之间的夹角，如图8所示。

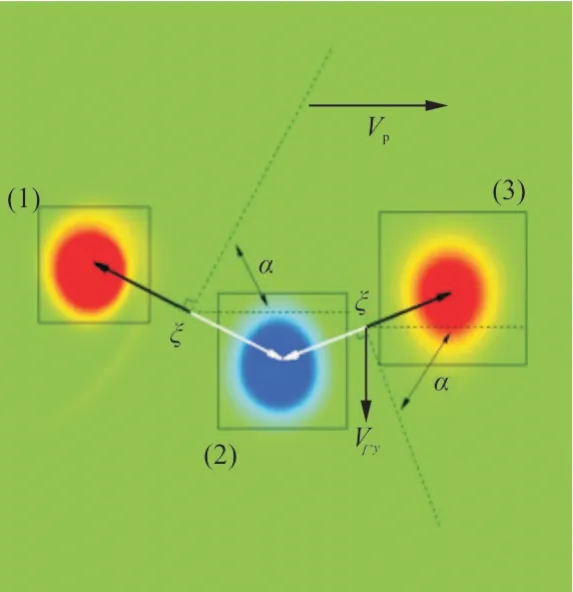
图8 流场中涡对的y 向诱导速度VГy计算示意图Fig.8 Calculation diagram of y-direction induced velocity VГy of vortex pair in flow field

随着漩涡不断向下游移动，细丝所在区域的向（竖直方向）流场诱导速度V的方向（向上或者向下）也会周期性变化，细丝的运动模式和方向上流场诱导速度V大小有关，同时也受漩涡向下游移动的速度影响，=d（）/d，（）是涡核时刻所在位置的坐标。当V的值比较大时，细丝会受流场力作用，在涡街一侧做自适应摆动运动，无法回到涡街中。本课题组前期工作发现，当比较大时，在细丝刚开始放入涡街的过程中，细丝没有足够的时间运动到涡街的外侧，便受到从上游传输过来的反向涡的诱导力，从而改变摆动方向，如此循环往复，在涡街中做绕核运动，如图9 所示。

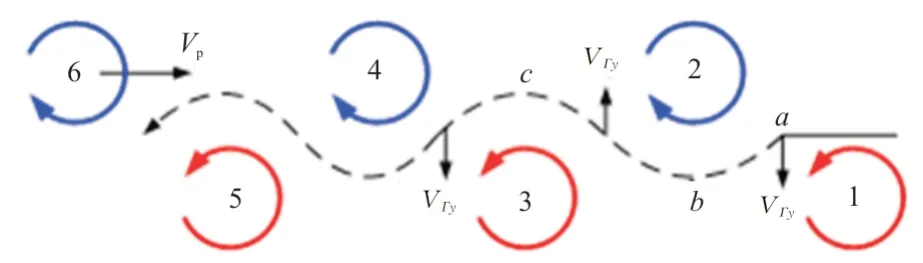
图9 细丝做绕核运动示意图［20，22］Fig.9 Schematic diagram of filament moves around the vortex cores［20，22］

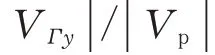
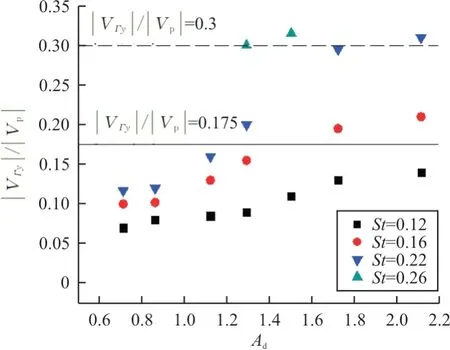
图10 在扑翼摆动参数（St，Ad）不同的条件下|VΓy|/|Vp|的值Fig.10 The value of||/|Vp|under different flapping parameters（St，Ad）

从图10 可以看出：

（1）当|V|/||＜0.175 时，细丝在涡街中做绕核运动。改变细丝的柔性，细丝的运动状态并不会改变，始终是做绕核运动。这是由于当|V|/||的值较小时，涡对在竖直方向上的诱导速度较小，且由于的值相对较大，细丝没有足够的时间朝涡街的上侧（或下侧）运动，便受到从上游传输过来的反向涡的作用，被迫改变运动方向，开始朝涡街下侧（或上侧）摆动，因此细丝一直在涡街中做绕核运动。

（2）当0.175≤|V|/||＜0.3 时，细丝在涡街一侧运动。但是，减小细丝柔性，细丝的运动状态会由在涡街一侧运动转变绕核运动。为了探究细丝运动状态发生改变所对应的̂值和|V|/||之间的关系，通过六组算例进行对比，如表2 所示。

表2 细丝的运动状态随刚度的变化关系Table 2 The motion state of the filament varies with the stiffness

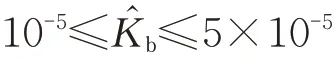
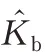
表3 值过渡区间与|VΓy|/|Vp|的对应关系Table 3 The corresponding relationship between transition interval and|VΓy|/|Vp|

（3）当0.3≤||/||时，细丝的运动状态为在涡街一侧运动，改变细丝的柔性，细丝依然保持在涡街一侧运动。由于V的值比较大，涡对在竖直方向上的诱导速度较大，且上游反向涡向下游传输的速度较慢，细丝有足够的时间运动到涡街的上侧（或下侧），在这种情况下，即使细丝的刚度较大，细丝也会被带到涡街外侧。

3 结 论

（1）本文提出了固定柔性分布、连续变柔性分布和分段柔性分布三种细丝柔性分布模式，在扑翼尾迹中（卡门涡街或者反卡门涡街），当其他参数相同时，改变细丝柔性，细丝的运动状态也会改变。

（2）细丝运动状态随柔性的变化规律受涡对在竖直方向上的诱导速度和涡向下游传输速度的共同影响，并且，刚度较大的细丝倾向于在涡街中做绕核运动，而刚度较小的细丝倾向于在涡街一侧运动。

柔性飞行器或自主水下航行器在进行编队航行时，应根据流场结构，对下游个体设置合适的柔性，使其能够始终保持在上游个体产生的尾迹一侧运动，达到减小阻力，节约能量的目的。