2016年全国卷I文科数学第20题的解法与探源

☉广东省东莞市第四高级中学 唐良生

2016年全国卷I文科数学第20题的解法与探源

☉广东省东莞市第四高级中学 唐良生

一、试题再现

题目 在直角坐标系xOy中，直线l：y=t（t≠0）交y轴于点M，交抛物线C：y2=2px（p＞0）于点P，M关于点P的对称点为N，连接ON并延长交C于点H.

（Ⅱ）除H以外，直线MH与C是否还有其他公共点？说明理由.

二、解法分析

（Ⅱ）直线MH与C除H以外没有其他公共点.理由如下：

点评：这个解法充分体现了坐标法思想，凸显了解析几何的解析味道，是学生必须掌握的方法，这个解法还从代数的角度证明了直线MH是抛物线过点H的切线.

解法二：（Ⅰ）同解法一.

（Ⅱ）如图1，作HH1垂直于准线垂足为H，交1y轴于点Q，由（Ⅰ）知△H1QM≌△FOM，从而∠H1MQ=∠FMQ，H1，M，F三点共线，由|HF|=|HH1|，|FM|= |H1M|，得HM是线段H1F的垂直平分线.

设直线MH上除H以外，与C还有一个公共点I，作准线的垂线II1，垂足为I1，连接IH1，IF，因为I是H1F垂直平分线上的点，所以|IH1|=|IF|.又I是抛物线y2=2px上的点，所以|II1|=|IF|，所以|IH1|=|II1|.

与△II1H1为直角三角形矛盾，所以除H以外直线MH与C没有其他公共点，即直线MH为抛物线的切线.

点评：这个解法紧扣抛物线的定义及平面几何的相关知识，回归本质，凸显了解析几何的几何味道.它不但从几何的角度证明了直线MH是抛物线过点H的切线，而且发现了直线MH就是“人教A版选修1-1，56页引入抛物线时图2.3-1中的直线m”，即线段FH的垂直平分线m，如图2所示.至此，这道高考题的起源就被找到了.

三、寻根探源

根据前面的分析，本题来源于人教A版数学选修1-1，56页：“信息技术应用：用几何画板画图，如图2.3-1，点F是定点，l是不经过点F的定直线，H是l上任意一点，过点H作MH⊥l，线段FH的垂直平分线m交MH于点M，拖动点H，观察点M的轨迹.你能发现点M满足的几何条件吗？”

教科书设置“信息技术应用”栏目，给出了抛物线生成的过程.通过几何画板的制作，学生可以从作法中了解曲线上的点所满足的几何条件，明确抛物线的定义，用几何画板作抛物线的方法，依据的就是这个栏目.但该栏目的作用绝不是仅此而已，它还给我们留下了如下宽广的探究空间.

探究1：点M的轨迹是抛物线C，那么与之相关的垂线m与抛物线C有什么关系呢？借助几何画板的跟踪轨迹功能，我们猜想它是抛物线的切线，点M为切点，如图3.

我们可以从代数和几何两个角度来证明垂直平分线m是抛物线过点M的切线，其证法与这道高考题的证法完全相同.至此，这道高考题就可以水到渠成地命制出来了.利用这个结论或者这道高考题的结论，如果知道抛物线的焦点、准线、对称轴、顶点中任意两个，就可以作出过抛物线上任意一点的切线.

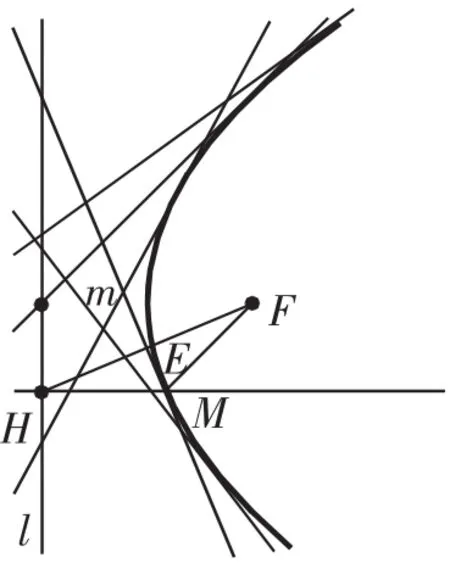
图3

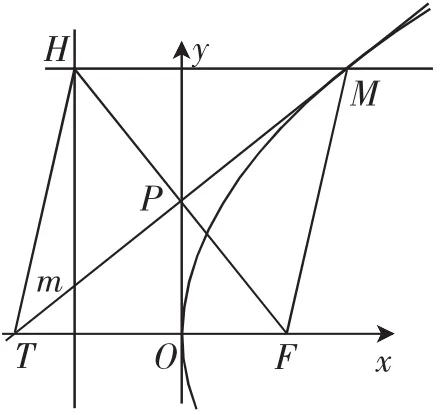
图4

探究2：如图4，若m与x轴相交于点T，则四边形MHTF为菱形.

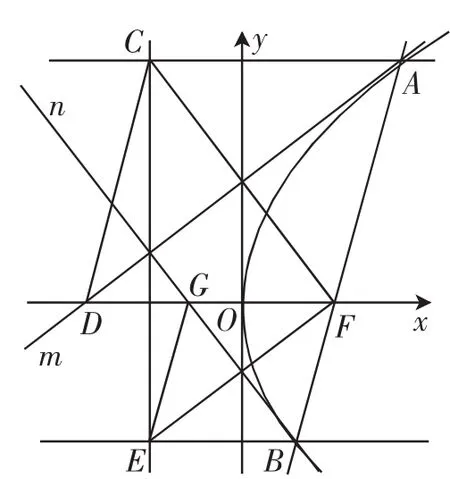
图5

探究3：如图5，AB为抛物线的焦点弦，作AC垂直准线于点C，作BE⊥准线于点E，作CF的垂直平分线m，交x轴于点D，作EF的垂直平分线n，交x轴于点G，得菱形ACDF和菱形BEGF，且菱形ACDF与菱形BEGF相似，相应对角线相互平行.

四、高考链接

下面再提供一道以直线m为背景的高考题.

例1 （2009年湖北卷文科20题）如图6，过抛物线y2＝2px（p＞0）的焦点F的直线与抛物线相交于M、N两点，自M、N向准线l作垂线，垂足分别为M1、N1.

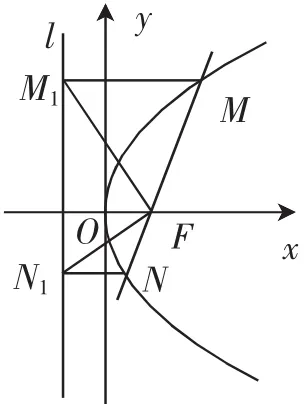
图6

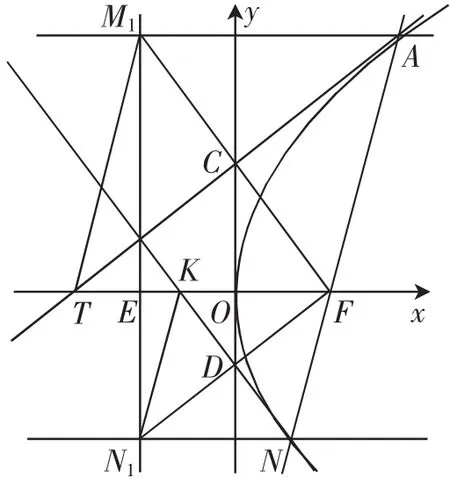
图7

（Ⅰ）求证：FM1⊥FN1；

（Ⅱ）记△FMM1、△FM1N1、△FNN1的面积分别为S1、 S2、S3，试判断是否成立，并证明你的结论.

分析：本小题主要考查抛物线的概念，抛物线的几何性质等平面解析几何的基础知识，考查综合运用数学知识进行推理运算的能力.证明方法很多，若作出线段FM1的垂直平分线m，作出线段FN1的垂直平分线n，菱形MM1TF的对角线M1F与菱形NN1KF的对角线N1F互相垂直，立即得FM1⊥FN1.

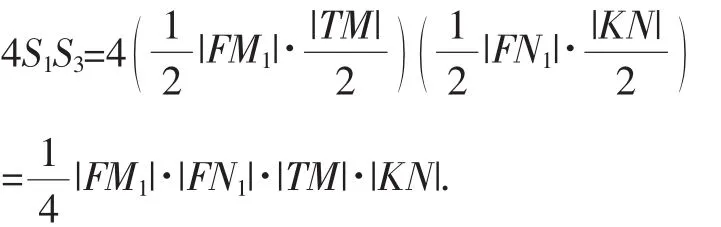
1.孔德泉.思题所解 叙己所思——2015年高考数学全国新课标Ⅱ理科第20题的拓展研究 ［J］.中学数学（上），2015（9）.

2.刘海亚.一条直线及其妙用［J］.中小学数学（北京），2011（4）.