复合函数中的几类问题辨析

☉江苏省海安县实验中学 杨兴红

复合函数中的几类问题辨析

☉江苏省海安县实验中学 杨兴红

复合函数是近几年高考的热点，是高中与大学重要的知识点和难点，笔者结合多年的教学实践谈谈复合函数中几类问题的解决.

一、复合函数的概念及基本性质

复合函数类似工厂连续经过几道工序加工一个零件，对应关系g先对x作用，得到g（x）为里层函数；然后对应关系f作用g（x）整体，得到f（g（x））为外层函数；复合函数与里层函数是同一个自变量x，里层函数g（x）是对应关系g对自变量x作用一次，而复合函数f（g（x））是对应关系g与f同时对自变量x作用两次，并且有作用的先后顺序，对应关系f后作用的是里层函数g（x）的整体，于是里层函数g（x）充当外层函数的自变量；里层函数的定义域就是复合函数的定义域，里层函数的值域就是外层函数的定义域；外层函数的值域就是复合函数的值域；复合函数f（g（x））的单调性概括为“同增异减”.

二、例谈复合函数的几类问题

1.定义域问题

复合函数的定义域问题是比较容易出错的，也是经常考查的重要问题，然而求复合函数定义域问题也是常错的一类题.

这道题相当于给出已知f（x）的定义域，求f［g（x）］的定义域.据自己所理解的是g（x）把前面的f（x）中x的位置给占了，而g（x）要能替代x就必须符合x的范围，就像并不是所有的人都能当主席，必须有能力才能在主席这个位置上混.形象的理解就是在f（⊗）中，现在g（x）要替代⊗的位置，就必须具备⊗所具有的性质.

由此总结出两个常见结论：

（1）已知f（x）的定义域，求f［g（x）］的定义域.

其解法是：若f（x）的定义域为a≤x≤b，则在f［g（x）］中，a≤g（x）≤b，从中解得x的取值范围即为f［g（x）］的定义域.

（2）已知f［g（x）］的定义域，求f（x）的定义域.

其解法是：若f［g（x）］的定义域为m≤x≤n，则由m≤x≤n确定的g（x）的范围即为f（x）的定义域.

这两个结论对不对呢？回到数学当中来，我们现在要由g（x）来确定f（x）的定义域是缺少条件的，我们求出来的g（x）的范围仅仅只是f（x）定义域的子集而已.

因为f（x）的定义域是R，而g（x）的值域是［1，+∞），则f［g（x）］的定义域是［1，+∞），这是不符合我们上面的求法的.

也就是说我们在没有明确说明g（x）完全等价于f（x）中的x时是不能直接判断g（x）的值域就是f（x）的范围的.

因此可以总结出：

（1）已知f（x）的定义域，求f［g（x）］的定义域.

其解法是：若f（x）的定义域为a≤x≤b，则在f［g（x）］中，a≤g（x）≤b，从中解得x的取值范围即为f［g（x）］的定义域.

（2）已知f［g（x）］的定义域，求f（x）的定义域.

其解法是：若f［g（x）］的定义域为m≤x≤n，则由m≤x≤n确定的g（x）的范围即为f（x）的定义域的子集.

2.点对称问题

在高三的教学实践中，常常遇到下面两个问题：

（1）已知函数f（x）=cosxsin2x，下列结论中正确的是（ ）.

A.y=f（x）的图像关于（0，π）中心对称

D.f（x）既是奇函数，又是周期函数

课堂讲解时，笔者对选项A、B分别验证f（2π-x）= -f（x）和f（π-x）=f（x）成立，判断A、B正确.课后学生问：老师此题若改为填空题，求函数f（x）=cosxsin2x的对称轴、对称中心怎么做，函数f（x）=cosxsin2x还有其他的对称轴、对称中心吗？

（2）在有关三角函数内容教学时，有一种重要题型，如：已知函数求函数的对称中心、对称轴.

性质1：设函数y=f（x）的定义域为A，函数y=g（x）的值域为B，B⊆A，函数y=f（x）的图像关于（b，c）对称，函数y=g（x）的图像关于（a，b）对称，则函数y=f（g（x））的图像关于（a，c）对称.

证明：因为函数y=f（x）的图像关于（b，c）对称，函数y=g（x）的图像关于（a，b）对称，所以f（2b-x）=2c-f（x），g（2a-x）=2b-g（x），设h（x）=f（g（x）），因为h（2a-x）= f（g（2a-x））=f（2b-g（x））=2c-f（g（x））=2c-h（x），所以函数y=f（g（x））的图像关于（a，c）对称.

注：内、外函数都是中心对称函数，且内函数图像对称中心的纵坐标等于外函数图像对称中心的横坐标，则复合函数图像是中心对称.

性质2：设函数y=f（x）的定义域为A，函数y=g（x）的值域为B，B⊆A.函数y=f（x）的图像关于x=b对称，函数y= g（x）的图像关于（a，b）对称，则函数y=f（g（x））的图像关于x=a对称.

证明：因为函数y=f（x）的图像关于x=b对称，函数y= g（x）的图像关于（a，b）对称，所以f（2b-x）=f（x），g（2a-x）= 2b-g（x），设h（x）=f（g（x）），因为h（2a-x）=f（g（2a-x））= f（2b-g（x））=f（g（x））=h（x），所以函数y=f（g（x））的图像关于x=a对称.

注：内函数是中心对称函数，外函数图像关于轴对称，且内函数图像对称中心的纵坐标等于外函数图像对称轴的值，则复合函数图像是关于轴对称.

性质3：设函数y=f（x）的定义域为A，函数y=g（x）的值域为B，B⊆A，函数y=g（x）的图像关于x=a对称，则函数y=f（g（x））的图像关于x=a对称.易证.

注：内函数图像关于轴对称，则复合函数图像也关于轴对称，简记为“内轴为轴.”

下面运用性质解决问题：

（1）求函数f（x）=cosxsin2x的中心对称、对称轴.

解析：由函数f（x）=2（sinx-sin3x），设y=-2t3+2t，t= sinx，y=-2t3+2t的对称中心是（0，0），t=sinx的对称中心是（kπ，0）（k∈Z），内函数图像对称中心（kπ，0）（k∈Z）的纵坐标等于外函数图像对称中心（0，0）的横坐标，根据复合函数图像对称的性质1，则所求函数图像的对称中心为（kπ，0）（k∈Z）.

y=-2t3+2t的对称中心是（0，0），t=sinx的对称轴是x=根据复合函数图像对称的性质3，则所求函数图像的对称轴是

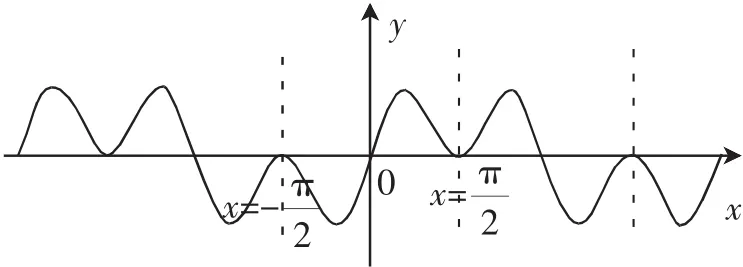
图1

图1是利用几何画板画出的函数f（x）=cosxsin2x的图像，可验证上述结论的正确性.

因此可知：复合函数的奇偶性是复合函数图像对称性质的特例.探究寻源，抓住问题的本质，才能使我们高屋建瓴地看待问题，理解掌握复合函数图像的对称性质，能使我们居高临下地处理此类问题，在我们在教学中游刃有余.

3.综合问题

复合函数问题也常常在综合问题中遇到，例如，新高考改革上海2015年理科数学23题考到复合函数对应关系，下以此例说明：对于定义域为R的函数g（x），若存在正常数T，使得cosg（x）是以T为周期的函数，则称g（x）为余弦周期函数，且称T为其余弦周期.已知f（x）是以T为余弦周期的余弦周期函数，其值域为R.设f（x）单调递增，f（0）=0，f（T）=4π.

（2）设a＜b，证明对任意c∈［f（a），f（b）］，存在x0∈［a，b］，使得f（x0）=c；

（3）证明：“u0为方程cosf（x）=1在［0，T］上的解”的充要条件是“u0+T为方程cosf（x）=1在［T，2T］上的解”，并证明对任意x∈［0，T］都有f（x+T）=f（x）+f（T）.

解析：（1）略.

（2）由于f（x）的值域为R，所以对任意c∈［f（a），f（b）］，c都是一个函数值，即有x0∈R，使得f（x0）=c.

若x0＜a，则由f（x）单调递增得到c=f（x0）＜f（a），与c∈［f（a），f（b）］矛盾，所以x0≥a.同理可证x0≤b.故存在x0∈［a，b］使得f（x0）=c.

（3）若u0为cosf（x）=1在［0，T］上的解，则cosf（u0）=1，且u0+T∈［T，2T］，cosf（u0+T）=cosf（u0）=1，即u0+T为方程cosf（x）=1在［T，2T］上的解.

同理，若u0+T为方程cosf（x）=1在［T，2T］上的解，则u0为该方程在［0，T］上的解.

以下证明最后一部分结论.

由（2）所证知存在0=x0＜x1＜x2＜x3＜x4=T，使得f（xi）=iπ，i=0，1，2，3，4.

而［xi，xi+1］是函数cosf（x）的单调区间，i=0，1，2，3.

与之前类似地可以证明：u0是cosf（x）=-1在［0，T］上的解，当且仅当u0+T是cosf（x）=-1在［T，2T］上的解，从而cosf（x）=±1在［0，T］与［T，2T］上的解的个数相同.

故f（xi+T）=f（xi）+4π，i=0，1，2，3，4.

对于x∈［0，x1］，f（x）∈［0，π］，f（x+T）∈［4π，5π］，而cosf（x+T）=cosf（x），故f（x+T）=f（x）+4π=f（x）+f（T）.

类似地，当x∈［xi，xi+1］，i=1，2，3时，有f（x+T）=f（x）+ f（T）.结论成立.

总之，复合函数问题，奥妙无穷，层层剥离，我们要深入仔细的研究，让中国数学达到世界的顶峰！F