对一道圆锥曲线问题的探究与拓展

☉陕西省靖边县靖边中学 徐永强

对一道圆锥曲线问题的探究与拓展

☉陕西省靖边县靖边中学 徐永强

一、题目展示

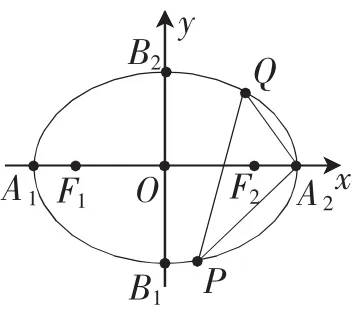
（Ⅰ）求椭圆C的标准方程.

（Ⅱ）过椭圆C的右顶点A2作互相垂直的两条直线分别交椭圆于另一点P，Q，试判断直线PQ是否过定点，若过定点，求出该定点的坐标；若不过定点，请说明理由.

二、挖掘条件，分析解答

此题属解析几何中经常考查的热点题型（定点、定值问题），其解题的方法体现了解析几何解决问题的通性通法，其中第（Ⅰ）问用待定系数法，第（Ⅱ）问首先联立方程，再用韦达定理，借助其他条件能很容易求解.

解：（Ⅰ）依题知

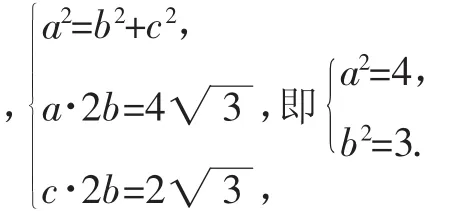
（Ⅱ）依题知，直线A2P与直线A2Q的斜率均存在且不为0，令P（x1，y1），Q（x2，y2）.

设lA2P：y=k（x-2），lA2Q消去y，得（4k2+3）x2-16k2x+4（4k2-3）=0.

解之，得k2=1，此时直线PQ的方程为即此时直线PQ过点

三、探求本质，推广结论

著名的数学之王、数学家苏步青说过：“学习数学要多做习题，边做边思索，先知其然，然后知其所以然”所以，当一道题目解答完后的反思尤为重要，解答题目本身是表象，推广、提升才能真正理解出题人的意图，才有助于学生走出题海无涯的困境，才能提高学生解题能力和效率.

那么，上述问题能否推广到所有的椭圆呢？答案是肯定的.

证明：先证过右顶点的情况：

令P（x1，y1），Q（x2，y2）

依题设：lA2P：y=k（x-a）.消去y，得（a2k2+b2）x2-2a3k2x+（k2a4-a2b2）=0.

由根与系数关系得

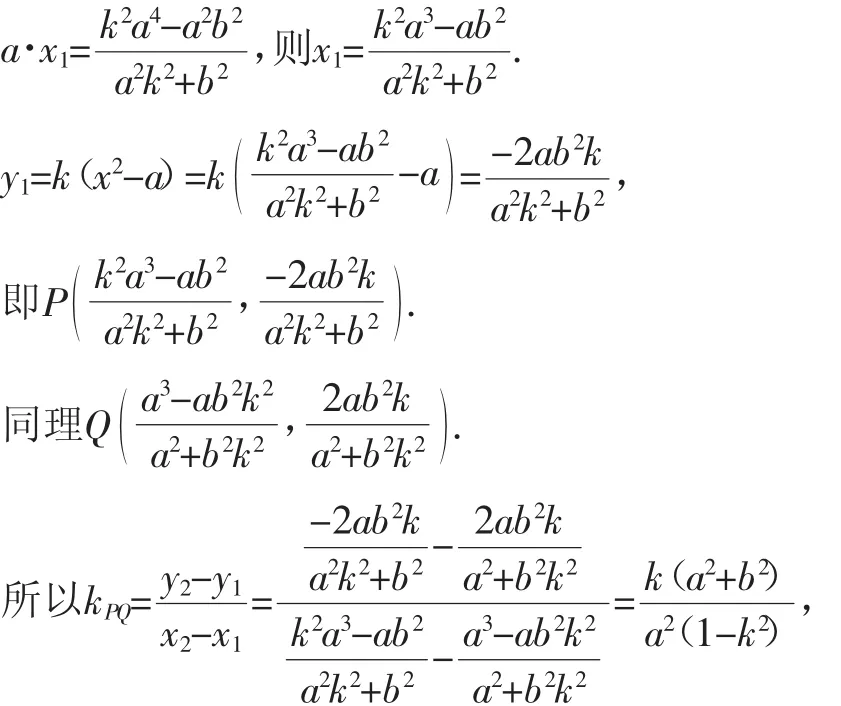
同理，可证过左顶点的结论.

（证法同上，略）

上述结论在椭圆中成立，那么在其他圆锥曲线中成立吗？

四、联想类比，延伸结论

证明：同性质1的证明过程.

结论4：过抛物线C：y2=2px（p＞0）的顶点O作互相垂直的两直线分别交抛物线于另一点P，Q，则直线PQ过定点（2p，0）？（p为抛物线焦点到准线的距离）.

证明：设直线直线PQ方程为x=ky+m，其交与抛物线于P（x1，y1），Q（x2，y2）.由消去y得y2-2pky-2pm= 0，

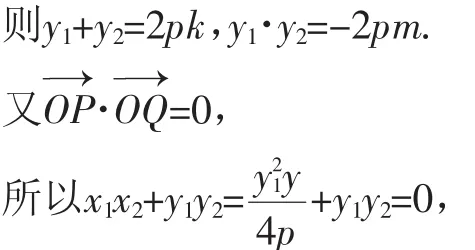
即m=2p或m=0（舍）.

故直线PQ过定点（2p，0）.

结论5：过圆C：（x-m）2-（y-n）2=r2上任意一点A2作互相垂直的两直线分别交圆于另一点P，Q，则直线PQ过定点（m，n）（m，n分别为圆心的横纵坐标）.证明略.

五、结束语

通过对上述结论的探究，我们进一步认识到椭圆、双曲线、抛物线等曲线，除了自身存在一定的规律性，圆锥曲线之间也存在一定的规律性，正如著名数学家高斯所言：“数学中的一些美丽定理具有这样的特性：它们极易从事实中归纳出来，但证明却隐藏的极深.”所以这种规律性，需要我们用坚强的意志、良好的数学素养去发现、挖掘.

1.贺建勋，段雄伟.习题生成问题中培养学生的探究能力［J］.中学数学教学参考（上），2015（11）.

2.郑日锋.求异 探源 启迪——对一道高考试题的剖析［J］.中学数学（上），2015（10）.

3.臧殿高.圆锥曲线的统一性质漫谈［J］.数学通报，2009（8）.