巧提问，引思维，得实效——试探高中数学课堂中的有效提问途径

☉江苏省如皋市搬经中学 符晓冬

巧提问，引思维，得实效
——试探高中数学课堂中的有效提问途径

☉江苏省如皋市搬经中学 符晓冬

数学知识的学习过程是一个动态的过程，无论是知识的理解，还是新问题的发掘，都需要在不断的思维拓展与相互激发中完成.因此，数学知识的呈现过程当中自然也应当将这个动态的特点反映出来.具体到高中数学的课堂教学之中，教师要做的就是让整个课堂“活”起来，告别传统的教师讲、学生听的刻板模式，让学生们主动融入到教学过程当中来，全方位激活学生思维，在师生之间的交流互动当中实现知识接受效果的不断提升.在教学实践之中，笔者为了能够为学生们创造一个全新的灵动课堂，让大家在不断思考当中切实感受数学，选择了在教学当中巧妙设置提问，并收获了颇为理想的教学效果.

一、将提问情境化，增强数学课堂教学趣味

在对课堂教学方式进行讨论时，我们经常会谈到“情境教学”的话题.的确，在数学课堂当中创设出相应的教学情境，能够将原本理论刻板的知识内容具体化、灵动化，降低学生们的思维门槛，更加顺利地理解知识.这种情境教学的思路，也应当渗透到课堂提问的设计当中来.如果教师能够向提问当中也加入知识情境的元素，定能够为数学课堂带来更多的趣味与热情.

例如，在解析几何中椭圆内容的课堂教学一开始，我便以这样一个提问作为开始：设有一颗彗星沿一椭圆轨道绕地球运行，地球恰好位于椭圆轨道的焦点处，当此彗星离地球相距m万千米时，经过地球和彗星的直线与椭圆的长轴夹角分别为求该彗星与地球的最近距离.这个问题的出现，很快将学生们的思维带入了这个航天的问题情境当中.结合着近年来我国航空航天事业的蓬勃发展，经常会出现相关新闻，学生们对这个问题的研究顿时很有兴趣.大家都很期待能够掌握椭圆的性质，让自己也能体会一下作为航天研究员的感觉.

情境化的提问方式，成功将学生们的关注重点迁移至了具体的知识氛围当中.比起平铺直叙地将抽象的知识内容摆在学生面前，这显然为学生们提供了一个舒适的氛围，让数学知识可以缓缓进入学生们的头脑当中.在面对主体知识之前，先让学生们在情境当中感受到它的趣味，就像是提前为接下来的有效教学做好了情感上的铺垫.学生们带着兴趣走进学习探究，效果自然是理想不少的.

二、将提问梯度化，降低复杂知识接受难度

高中阶段的数学教学不同于之前的一个很重要的特点就在于，这期间的知识难度表现出了显著提升，也为很多学生们造成了理解掌握上的困难.为了将学生们的数学思维提升至教学所要求的高度，课堂提问自然也需要达到相应的难度.然而，这就引发了一个矛盾：若提问的难度不够，显然无法完成预设的教学目标；但若提问的难度过大，不仅学生们无法妥善接受，甚至还容易产生抵触心理，影响日后学习.为了解决这个问题，笔者尝试了设置梯度化问题的方式，取得了较好的教学效果.

例如，在对抛物线的内容进行教学时，我向学生们提出了这样一个问题串：

抛物线y2=2px（p＞0）上有两个动点A，B及一个定点M，F为焦点，若|AF|，|MF|，|BF|成等差数列，则

（1）求证：线段AB的垂直平分线过定点Q；

（2）若|MF|=4，|OQ|=6（O为坐标原点），求抛物线的方程；

（3）对于（2）中的抛物线，求△AQB面积的最大值.

如果直接将最后一个问题摆在学生面前，难免会让大家感到措手不及.但通过以上三个梯度化问题的铺垫与递进，学生们接受起来显然容易多了.在一个个问题的思考当中，也为后面更深入问题的解答做好了先期准备.

可以看出，这样的提问设置方式，就像是为学生们的思维深入搭建了一级级阶梯，虽然最终所达到的高度是相同的，但每一级阶梯的高度却减少了许多，自然也就降低了学生们在思维深入过程当中所要承受的难度.与此同时，难度较小的问题也可以预先引发出之后难度稍大的问题，可以让学生们在思考当前问题的同时为接下来的内容做好思维准备.对于疑难复杂的数学内容教学来讲，梯度化的课堂提问设置是非常适用的.

三、将提问探究化，有效提升数学思维能力

当然，为了促进学生灵活思维的拓展，作为思维活动的导引，课堂提问也绝不能仅仅停留在基础知识的范围之内.对于拓展性比较强的内容，相应的提问也需要随之铺展开来.这个过程表现在教学实践当中，就是探究化提问的使用.通过问题的巧妙提出，带领学生们走出基本的知识范畴，通过自己的力量去继续打开全新的知识视野，也就实现了高中数学学习境界的提升.

例如，在立体几何内容的教学中，为了灵活大家的思路，我设计了如下问题：

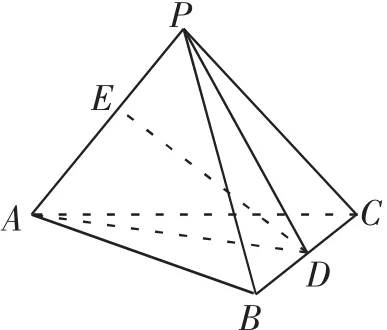
图1

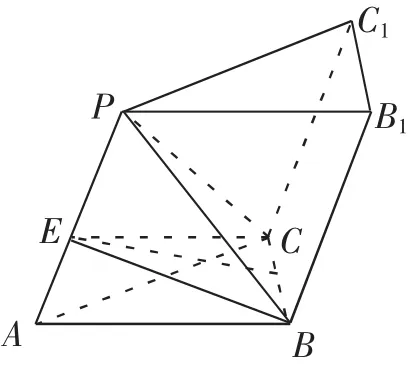
图2

如图1所示，三棱锥P-ABC中，已知PA⊥BC，PA= BC=n，PA与BC的公垂线DE=h，求证：三棱锥P-ABC的体积V=n2h.并提出要求：从“割形”与“补形”的角度入手进行证明.虽然这道题的证明方法不少，但割补的方式却是学生们较少注意到的.这个角度的思考，无疑是学生们开展的一个全新角度的探究.果然，大家创新视角，在图1中通过连接AD和PD顺利求证.还有学生想到，还可以以三棱锥P-ABC的底面为底面，PA为侧棱，补成三棱柱PB1C1-ABC（如图2），连接EC、EB，同样得证.这个新思路的探究过程，让学生们的头脑进一步充实了.

在探究化提问的引领之下，灵活多样的探究活动在高中数学教学课堂上顺利展开了.为了发现知识内容的深层次面貌，探究活动必不可少.然而，如果探究的要求总是由教师以硬性要求的方式提出，难免让学生们感到突兀而难以接受，或是始终在被动的心理状态下加以完成.将探究的要求融入到提问当中，很好地化解了这个矛盾.学生们为了解答当前问题，会很自然地开始探究，从思维上反客为主，在内在需求的驱动之下实现深入教学的良好效果.

四、将提问适时化，发挥课堂问题最大效能

虽然问题的提出是高中数学课堂教学的必要组成部分，但是，这也并不表示问题可以被任意地提出.除了全文当中所提到的问题内容与形式上的注意之外，提问所处的时间也颇为重要.如果能够将课堂提问做到适时，便可以将学生们的注意力集中在最有价值的地方，在大大节省课堂教学精力的同时，达到最高质量的教学效果.何时需要学生们展开思考，就是教师需要仔细斟酌的问题.

例如，在对等差数列的基本知识教学完成后，学生们普遍感到，这部分内容的难度似乎不是很大.这时，我马上请学生们试着解答如下问题：将一个骰子连续抛掷三次，它落地时向上的点数依次成等差数列的概率是多少？虽然是以等差数列为背景的问题，但大家明显感受到解答起来难度不小.这个问题的分析，不仅需要根据等差数列的特点对抛掷骰子的情况进行分析，还要对之加以清晰分类，根据“公差为0的有6个”、“公差为1或-1的有8个”、“公差为2或-2的有4个”这三种情况进行分类，既要做到不遗漏，也要做到不重复，最后进行计算.由此学生们感受到，等差数列并不是简单的数字罗列，将之运用到具体问题解答时，还需要结合许多数学思想方法.

如此看来，看似随意的课堂提问也是需要精心计划与设计的.引导学生们将有限的思维精力集中适用在最需要的知识内容上，是富有实效的课堂教学所必不可少的支持元素.于该思考处设问，于该深入处设问，是有效的课堂提问所应追求的.

数学知识的深化理解离不开一个个问题的推动，因此，从课堂提问入手，以巧妙设计的数学问题，让学生们将注意力聚焦到重点难点问题上，并通过对具体问题的思考实现对相应知识内容的灵活感知，是当前高中数学教学高效开展的合理途径.从前文当中的论述也不难发现，课堂提问的方式与特点有很多，所对应的教学效果也是有所差异的.在实际教学过程当中，教师应当根据具体的教学内容进行分析，根据知识特点与教学需求来设计提问，既能够达到预期的知识呈现效果，又能够让适度变化的提问方式为学生们带来新鲜的课堂学习体验，可谓一举两得.相信有效的课堂提问途径，定会为高中数学课堂带来显著优化的教学实效.

1.韩小平.“问题串”教学的探索与实践［J］.数学教学通讯，2014（27）.

2.徐海兵.以学生主体为出发点的高中数学教学研究［J］.新课程导学，2016（8）.

3.张琴.高中数学课堂提问的案例分析［J］.新课程（中学），2016（1）.