源于一道教材习题的高三复习课

☉浙江省湖州市吴兴高级中学 刘晓东

源于一道教材习题的高三复习课

☉浙江省湖州市吴兴高级中学 刘晓东

一、引言

高三复习是一个系统工程，对于学生而言，高三复习是对数学知识的再学习，是把数学知识进行巩固和内化，形成知识体系，逐步提高分析和解决问题的能力；对于教师而言，通过高三复习课教学，进一步激发学生对数学的兴趣，帮助学生构建科学的知识网络，促进学生对数学思想方法的理解和掌握.如何提高复习课的效率？始终是高三教学永恒的话题，现实中，我们不难发现，很多学校、很多老师的高三数学复习，都是围绕教辅资料一轮、二轮甚至三轮、四轮，机械地重复与练习仿佛成了高三数学复习的全部，教师缺乏对复习课深刻的理解与精心设计，成了教辅资料的奴隶，学生则成了解题的工具，数学能力依旧在原地徘徊，很难有质的飞跃.

要改善复习课的教学现状，关键在教师.教师用教辅资料无可厚非，但不能只是教辅的搬运工，应致力于对复习课的教学设计，加强对教材的深刻理解及适度开发、挖掘.教材是数学知识、方法、思想的重要载体，是产生高考题的主要来源，相当数量的高考题源于教材，即使是综合题，也是基本题的组合、加工和发展，高考试题万变不离其宗.纵观高考学生答题情况，考生在答题中的大部分失误，并不是因为缺乏灵活思维，而是对基础知识、基本定理的掌握存在不足，对知识理解往往是片面的、孤立的、肤浅的，不能形成完整合理的知识体系和深层次的理解，这些原因的产生与学生在高考复习中脱离教材有很大的关系.脱离课本，导致的直接后果就是严重影响了学生对基础知识的牢固掌握，在复习过程中，教师应有意识、有目的地对教材中典型的例习题进行反思探讨，挖掘例习题的内涵和外延，在变换中培养学生解决“新问题”的能力，达到“知新”的目的.本文是源于一道课本习题的高三复习课，旨在引玉.

二、源于一道教材习题的高三复习课教学设计

环节一：原题再现

原题 （人教A版必修4第102页第4题）如图1，设Ox、Oy是平面内相交成60°角的两条数轴，e1、e2分别是与x轴、y轴正方向同向的单位向量，若向量则把有序实数对（x，y）叫作向量在坐标系xOy中的坐标.假设

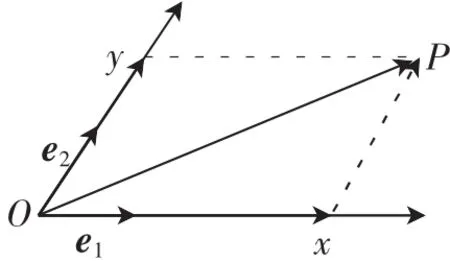
（2）由平面向量的基本定理，本题中向量坐标的规定是否合理？

变式拓展：过点P作直线l分别与x轴、y轴交于点A、B，确定A、B的位置，使△OAB的面积最小，并求最小值.

设计意图：原题是教材中一道非常经典的习题，内涵丰富.通过原题再现，让学生重温经典（有的学生可能根本就没做过），但并不是为了解题而解题，主要是让学生通过解题体验斜坐标系的思想.对问题（1）两种方法的处理，既体现了向量运算的统一性，也体现了斜坐标系自身的特点；对问题（2）的解读，即对平面向量的基本定理进行了复习，也说明了斜坐标系的合理性.为了强化学生对斜坐标系的体验，设计了一个简单的变式，为斜坐标系的引入奠定基础.

环节二：斜坐标系的引入

1.斜坐标系的定义

在平面坐标系中，如果x轴和y轴相交成任意的角θ（不一定是直角），如图2，经过平面内一点P作坐标轴的平行线PM和PN作为P点的x坐标和y坐标，这样的坐标系叫作斜坐标系.

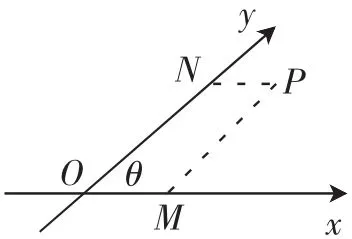
图2

2.斜坐标系的几个结论

（1）斜坐标系也可分为四个象限，各象限点的坐标及符号与直角坐标系定义方式相同.

（2）平面向量中的结论在斜坐标系中成立，且十分方便（基底即有方向的单位长）.

（3）斜坐标系中的直线方程可以利用直角坐标系中的截距式方程.设m、n分别是直线l在x轴、y轴上的“截距”，则l的方程为过原点的直线方程为y=tx.

（4）在斜坐标系中x+y=k为一族平行直线，类比直角坐标系，k为两轴上的“截距”.

3.斜坐标系下的“四象九域”

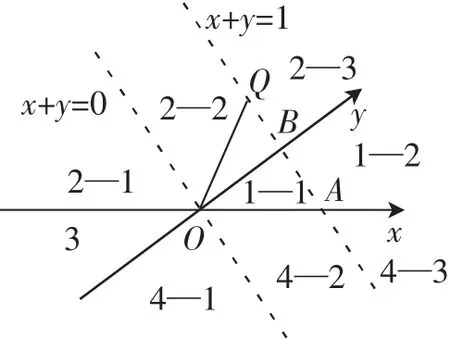
图3

类比直角坐标系下线性规划知识可得：（不妨记1—1区域为第一象限1号区域，其余类似，共九个区域）

设计意图：教材在平面向量的学习中安排这个习题，是有一定含义的，平面向量中的结论在斜坐标系中成立，说明了斜坐标系对向量的意义.在本环节的设计上，突出斜坐标系的定义，在这点上学生是很容易接受的，但有了定义，学生还不一定会用，为此，又给出了斜坐标系的几个相关结论及“四象九域”，为学生的应用提供更多的抓手，特别是与线性规划的结合，充分体现了直角坐标系与斜坐标系的内在联系及一致性.

环节三：斜坐标系下的向量问题

1.利用“四象九域”解题

例1 （2016年浙江统测文）已知平面向量a，b，c，满足c=xa+yb（x，y∈R），且a·c＞0，b·c＞0.下面结论正确的是（ ）.

A.若a·b＜0，则x＞0，y＞0 B.若a·b＜0，则x＜0，y＜0

C.若a·b＞0，则x＜0，y＜0 D.若a·b＞0，则x＞0，y＞0

解析：因为a·c＞0，b·c＞0，若a·b＜0，则可建立如图4所示的斜坐标系，则向量c在第一象限，所以x＞0，y＞0，故选A.

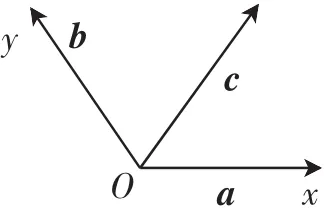
图4

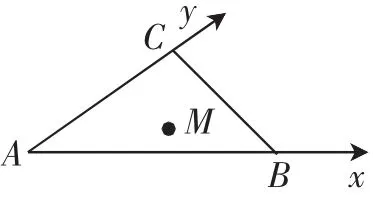
图5

变式1：（2016年北京市朝阳区高三一模）已知M为三角形ABC内一点（不含边界）则实数n的取值范围是______.

解析：如图5，以AB为x轴，以AC为y轴建立斜坐标系，AB、AC分别为x轴、y轴方向上的单位长度，则BC的方程为x+y=1，因为M在三角形内部，所以n＞0，且所以

图6

变式2：（2006年湖南理15）如图6，OM∥AB，点P在由射线OM、线段OB及AB的延长线围成的区域内（不含边界）运动，且，则x的取值范围是_________；当时，y的取值范围是_________.

解析：以OA、OB分别为x轴、y轴建立斜坐标系，如图6，OA、OB为单位长，则AB的方程为x+y=1，OM的方程为x+y=0，由点P所处位置，则x＜0，0＜x+y＜1，因为所以

设计意图：“四象九域”是斜坐标系的基本要素，为了让学生更好地理解斜坐标系，掌握斜坐标系的应用，特设计例1和两个变式，这三个问题利用“四象九域”来解决，显得尤为自然和简捷，学生也能够很快掌握，当然，我们也不能否定其他的解法.

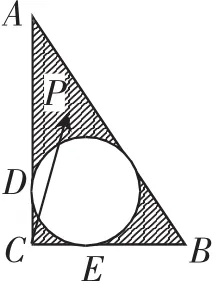
图7

2.斜坐标系与线性规划的结合

例2 （2016年杭州一模）在直角△ABC中，∠C是直角，CA=4，CB=3，△ABC的内切圆交CA、CB于点D、E，P是图7中阴影区域内的一点（不包含边界），若则x+y的值可以是（ ）.

A.1 B.2 C.4 D.8

解析：分别以CB、CA为x轴、y轴建立直角坐标系，易知△ABC内切圆半径为1，则DE的直线方程为x+y=1，此时显然不合题意，把DE适度上下平移，易知只有x+y=2满足题意，故选B.

例3 （2015年东北四校联考）已知点A（1，-1），B（4，0），C（2，2），点P满足则点P（x，y）组成的平面区域的面积为（ ）.

A.2 B.4 C.8 D.12

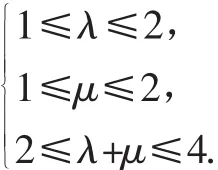
如图8，建立斜坐标系，结合线性规划知识，则点P（x，y）组成的平面区域为图中的阴影部分，其面积为三角形ABC面积的2倍，故选C.

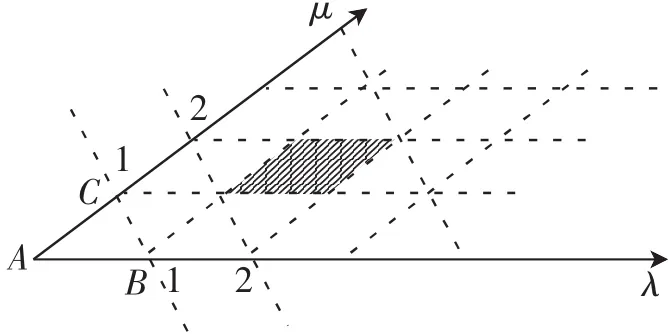
图8

变式3：（2016年绍兴市高三第一学期高三期末）正△ABC的边长为1，向量则动点P所形成的平面区域的面积为______.

解析：仿照例3建立斜坐标系，易求得动点P所形成的平面区域的面积为

设计意图：本环节的设计以直角坐标系导入，通过例3和变式3的设计，让学生充分体验利用斜坐标系处理向量问题的快捷，大大减少了思维量，从斜坐标系的视角处理线性规划问题，学生掌握的不仅仅是一种方法，更是对思维的一种提升，是对数学更深刻的理解.

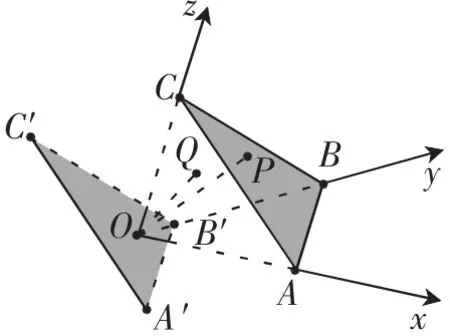
图9

3.由平面向空间拓展

例4 如图9所示，点O∈平面A′B′C′∥平面ABC，点Q在三棱锥O-ABC内部运动（不含边界），记则x的取值范围是_________.若时，则y+z的取值范围是________.

解析：如图9建立空间斜坐标系，结合线性规划知识，易得x＞0，y＞0，z＞0，且0＜x+y+z＜1，所以x的取值范围是0＜x＜1.若所以

设计意图：本环节的设计是将斜坐标系由平面推广到空间，旨在开拓学生的思维空间，学生的理解也是水到渠成，以例1为基础，本解法自然流畅，给人耳目一新之感.考虑到学生认知基础，此处不易过度拓展，否则也不符合高考要求，所以本环节只安排一个例题，也没必要设置变式.

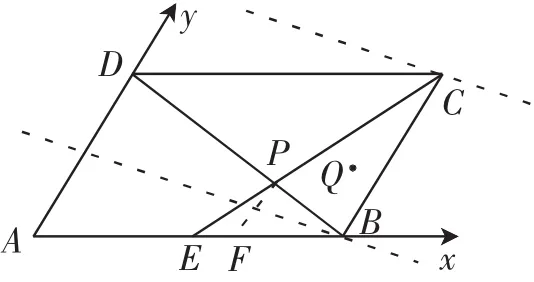
图10

4.活用斜坐标系直线的“截距”

例5 （2016年稽阳联谊高三联考）如图10，在平行四边形ABCD中，E是AB的中点，BD与CE相交于点P.若A→P=xA→B+则2x+y=______；若Q是△BCP内部（含边界）一动点，且则m+2n的取值范围为______.

解析：如图10，分别以AB，AD为x轴，y轴，AB，AD为单位长建立斜坐标系，因为E为AB的中点，过点P作PF∥AD，则易得P点坐标为所以

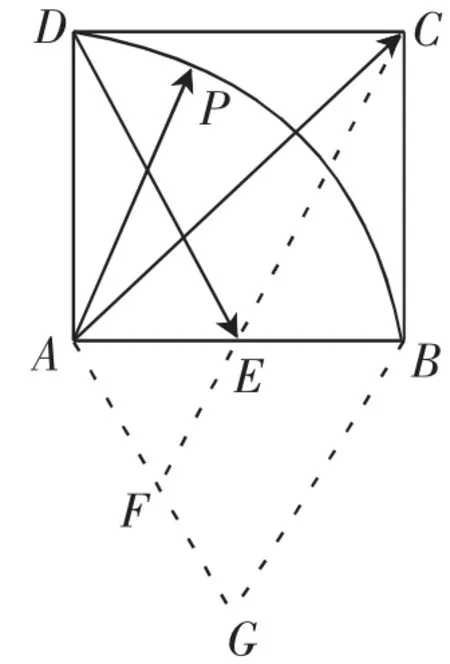
图11

例6 （2011届苏锡常镇扬五市调研）如图11，在正方形ABCD中，E为AB的中点，P为以A为圆心、AB为半径的圆弧上的任意一点，设向量则λ+μ的最小值为______.

设计意图：斜坐标系下直线的“截距”式方程是斜坐标系的亮点工具之一，有着美丽的几何意义，本环节通过两个例题的设置向学生充分展示了它的应用.对于学生而言，初用斜坐标系可能一时还无法适应，思维还会停留在原有的习惯上，但通过一定的训练，学生会很快接受的.对于这两个例题，我们既可以用几何法解决，也可以通过基底思想进行求解，但我们从斜坐标系的视角来处理，指向更为明确，只要合理的建系，问题便可迎刃而解.

三、教学反思

1.恰当地处理好课本与复习资料的关系

如何用好复习资料，让它发挥最大的效益，如何处理好课本与复习资料的关系，这是高三复习过程中首先要解决的一个基本问题.教材是教学的蓝本，无论是学生还是教师都要给予足够的重视，尤其教材中比较经典的习题，我们更应花大力气去研究、探讨，甚至是去拓展，本案例通过对一道课本习题的开发与拓展，并与高考热点相结合，收到了较好的复习效果.

2.对于教材习题拓展应适度

高三复习过程中，最难把握的就是教学的难度问题.对于教材习题拓展到什么程度，也是值得探讨的问题.本节课笔者在三个不同层次的学校都上过，教学效果也大相径庭，基础好的学校效果明显要好.对于基础差一点的学生而言，并不是他们接受不了，而是对斜坐标系毫无概念，让其在一节课之内完全接受，难度可想而知.事实上，对教材习题的研究不仅仅是在高三，而应该贯穿在我们教学的全过程中.

3.让高三数学复习课的课堂真正“活”起来

高三数学以复习课为主，传统做法是大容量、大密度，以老师讲为主，学生被动地接受，在课堂上基本上是围绕着教辅资料转，围着题目转，师生都成了解题机器，复习效果往往事倍功半.事实上只要我们把头抬起来，看看教材，研究一下教材习题，我们会发现一片新天地.本案例的意图就是要打破常规，从研究教材的视角向学生传递一个信息，教材是根，课本才是我们高三复习的根本.从实际教学来看，这样的复习课学生的参与度明显提高，课堂真正活了起来，虽然本节课的教学设计，在容量、难度等处理上有很多值得商榷的地方，但学生还是比较欢迎，效果也比较理想.

著名数学家G.波利亚说过：“一个专心的认真备课的教师能够拿出一个一个有意义但又不太复杂的题目，去帮助学生发掘问题的各个方面，使得通过这道题，就像通过一个门户，把学生引入一个完整的理论领域.”事实上，教材中的习题是编者从茫茫的题海中经过反复筛选，精心选择出来的，在解题思路和方法上具有典型性和代表性，在由知识转化为能力上具有示范性和启发性.本案例正是基于这种思想，通过对一道教材习题背景的揭示与拓展，去诠释研究数学教材习题、开发教材习题的必要性，从而提高高三数学复习课的效率.

1.沈新权.MPCK视角下的高中数学复习课教学［J］.中学数学（下），2016（3）.