浅谈思维定势下的错题成因与应对

☉江苏省南通市通州区教学研究室 王惠清

浅谈思维定势下的错题成因与应对

☉江苏省南通市通州区教学研究室 王惠清

定势思维是非常常见的思维积累后的一种运用表象（德国心理学研究者克劳斯语）.良好的思维定势对于我们解决问题有极大的帮助作用，在中学数学教学中最常见的思维定势运用体现在问题解决的模式识别中，这是思维定势比较积极的一面.从双基教学的扎实程度来看，思维定势积极的一面的确能帮助很多学生解决典型固定模型问题，但是随着教学整合的加深，笔者发现学生在问题解决过程中的难度也愈来愈大，不少学生（特别是偏文型的学生）总是不停地搜索脑海中的固有模型，或者总是问这样的数学问题有没有固定思维或模式可套用，这是典型的思维定势的表象之一.

从教育心理学的角度来说，思维定势最大的不足有两个方面：其一，僵化知识的串联，抹杀了知识间的穿插使用，这等于告诉学生代数问题代数解决，而没有另外角度的思考，这种僵化对于学生知识的连贯度有重大的阻碍作用；其二，创新能力的不足，过于在思维定势中纠结，往往让学生对问题解决的创新精神发挥不足，这对于学生长期的成长来说有一定的阻碍作用.因此，教师教学中必须对学生依赖思维定势进而形成的错误要及时关注和应对，用发展的眼光来看待模式识别，积极发挥其优势作用而减少其消极的影响.来看一下高中数学中常见的一些由思维定势而引起的错解和漏解.

一、思维缜密性不足

思维缜密性不足是定势思维解决问题中的常态错误.学生对于思维的常见僵化在于问题求解的惯性，一旦思维惯性使然，学生就将问题思考变得无意识化，从而问题的解决转变为一种定势思维下的机械化操作，思维的缜密度大大下降，导致错误产生.

问题1：已知集合A=｛x|x2+x-6=0｝，B=｛ax+1=0｝，满足B⊆A，求实数a能取的一切可能值所组成的集合.

错误分析：这是由事物表象迷惑引起的思维定势，学生将“ax+1=0”简单地看成是一个一元一次方程，而忽视了a=0的情况.事实上，当a=0时，B=Ø，显然满足B⊆A，因此正确的结果是

变式：当a为何值时，不等式（a2-1）x2-（a-1）x-1＜0的解集为全体实数？

错误分析：学生将原不等式简单地看成一个一元二次不等式，被它的表象所迷惑，产生了解题上的思维定势.事实上，当二次项系数a2-1=0时，即a=±1时，它并不是一元二次不等式，经过分类讨论知，当a=1时，也满足题意，故本题正确的解集为

二、思维全面性缺失

定势思维常见的第二种错误是思考问题的片面性，这种片面性形成的主因是教学对知识全面性使用的忽视，造成了思维定势.比如，等比数列求和公式中公比是否为1的讨论，公式使用过程中对于公比为1的情形一般较少遇到，导致了学生思维定势在公式使用过程中只考虑公比不为1的情形，造成了思考全面性缺失的错误.

问题2：求和Sn=1+2x+3x2+…+nxn-1.

错误解法：因为Sn=1+2x+3x2+…+nxn-1①，则xSn=x+ 2x2+3x3+…（n-1）xn-1+nxn②.

①-②得（1-x）Sn=1+x+x2+…xn-1-nxn，所以Sn=

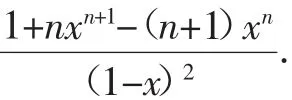
错误分析：错误的原因是缺少对x=1或x≠1时的讨论.由于我们在计算等比数列的求和问题时，常见的等比数列的公比不是1，因此，有不少学生在解题时产生了思维上的定势，只注重公式的“核心”部分，而忽视对特殊情况的考虑（例如本题中公比x=1），从而产生了顾此失彼的现象.

问题3：已知直线l：y=kx+1，抛物线C：y2=4x，问：当k为何值时直线l与抛物线C只有一个公共点？

错误分析：由于有不少学生对直线与圆的位置关系判断中，直线与圆只有一个公共点时判别式Δ=0这种方法记忆深刻，从而产生了解题思维上的一种定势，而忽视了当直线l与抛物线C的对称轴平行时，即只有一个公共点这种特殊的现象.

变式：求曲线y=3x-x3过点A（2，-2）的切线方程.

错误解法：因为导函数y′=3-3x2，又点A在曲线上，所以k=y′|x=2=-9，解得该曲线的切线方程为9x+y-16=0.

错误分析：不少学生在学习曲线的切线方程时，只知道过光滑曲线上一点，一定有一条直线和已知曲线相切，并且该点即为切点，但忽视了这一点可能是曲线的另一条切线与该曲线的交点.从根本上讲仍然是学生认为过曲线上一点至多有一条直线与已知曲线相切，就好像是直线与圆一样，这种狭隘的思想根深蒂固.

正确解法：设切点坐标为（x0，y0），因为导函数y′=3-3x2，所以又由直线方程的两点式得k=从而有解得x=-1或0x0=2，故切线的斜率k=0或k=-9，因此切线方程为y+2=0或9x+y-16=0.

三、思维转化度不足

思维转化度是体现学生数学学习知识是否灵活的重要评判标准，而长期训练会导致这样那样的思考定势，让学生在某些问题的处理上往往失去灵性.有时思维不能及时转化，还导致了学生在方法选择上的单一，甚至是因为方法选择的困难导致最终无法得到正确的答案，这些都是思维转化度不足的表现，因此教师教学要引导学生多角度地思考来解决问题，弱化思维定势，及时形成应对解决.

问题4：等差数列｛an｝的前n项和Sn=m，前m项和Sm=n（m≠n），求前m+n项的和Sm+n.

思维定势解答：设｛an｝的公差为d，则由Sn=m，Sm=n

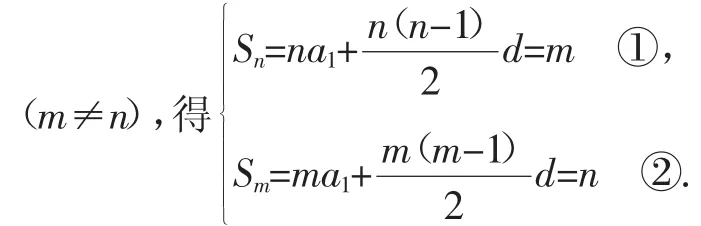
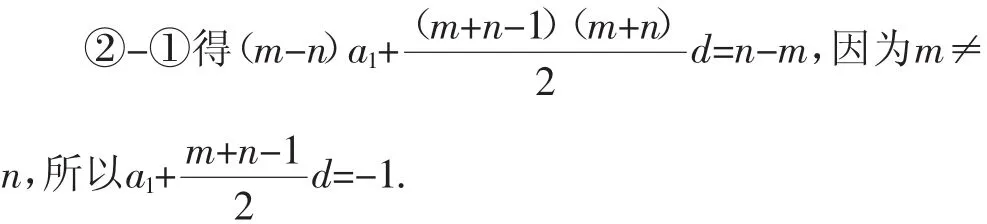
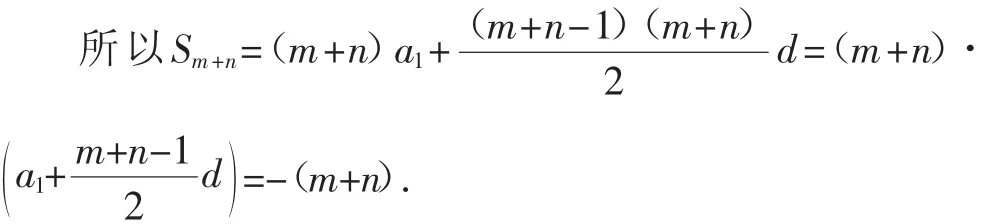
思维转化下的突破：设Sn=An2+Bn（n∈N*），则

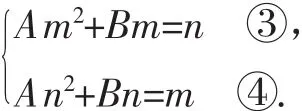
③-④得A（m2-n2）+B（m-n）=n-m.因为m≠n，所以A（m+n）+B=-1.

所以A（m+n）2+B（m+n）=-（m+n），所以Sm+n=-（m+n）.

说明：这是笔者给学生进行的一次数列测试中的问题，令笔者失望的是，绝大多数学生都是用第一种思维定势下的解决方式在处理，学生对于本题的解答是典型的定势思维：只要解决首项和公差，必定可以求解Sm+n，这是思维方式比较简洁的解法，但是实际操作如何呢？大多数学生花费了较多的时间运算，却最终没能得到正确的答案.考虑到条件的对称性，本题的解决思路从数列的函数本质入手，这样会更为简洁和轻快.

总之，与任何事物存在两面性一致，思维定势既有其优点，也存在其不足.让学生在不断扎实典型问题思维的基础上，进行有效的、有创造性的发展，是我们提高学生思维发展和应对定势思维存在缺陷最好的手段.从教学一线得到的经验来看：

首先，加强数学基础知识教学，重视知识的形成过程.在教学中，我们不仅要使学生牢记相应的知识，而且要使学生在掌握知识的同时，得到思维能力方面的提高.有不少学生认为学习定义、定理、公式等，只要记着就行了，对定理的证明，公式的推导很少能给以足够的重视.甚至有不少教师也往往只重视让学生把定义、定理、公式正确地、全面地接受下来，而不去探讨它们的由来和实质，缺少对相应定理或公式的证明和推导，忽略其证明和推导的原因.这样学生只会机械地记公式，套定理，而忽视了运用的前提和条件，一来学生很难记忆这些公式和定理，二来也很容易造成解题和思维上的某种定势.

其次，应当指出，任何事物都有它的两面性，数学中的思维定势并非纯粹只有消极影响，它也有好的一面，例如，正确的思维方式可以帮我们建立完整的解题模式，可以带来解题上的方便，节约不少的时间.因此，教师真正要做的是如何加深学生对概念、公式、定理和方法的理解，如何使学生学会正确的思考，培养学生合理解决数学问题的能力，从而有效地避免由思维定势所产生的消极影响.

1.傅瑞琦.试题分析让教研更精彩［J］.中国数学教育，2012（3）.

2.曹凤山.你能看出结果吗？——以一道例题的探究为例［J］.中学数学教学参考（上），2011（9）.

3.宋卫东.从生“动”到生动，诠释思维品质的提升［J］.中学数学月考，2013（5）.