考虑大幅值输入的随机子空间识别*

秦世强， 康俊涛， 周旺保

(武汉理工大学土木工程与建筑学院 武汉，430070)



考虑大幅值输入的随机子空间识别*

秦世强， 康俊涛， 周旺保

(武汉理工大学土木工程与建筑学院 武汉，430070)

随机子空间识别是一种可靠的时域模态参数识别算法，通常是利用结构在零初始状态作用下的动力响应来识别结构模态参数，而并没有考虑大幅值输入对识别结果的影响。针对此问题，研究了大幅值输入对随机子空间识别的影响并探讨了方法的适用性。首先，介绍了考虑大幅值输入的随机子空间识别理论基础；然后，通过一个两自由度系统进一步考虑了不同阶次模态、模态振型的相对精度随采样数和大幅值输入的变化情况；最后，以菜园坝长桥大桥拱肋脉动试验为算例，研究了考虑大幅值输入识别方法的适用性。结果表明：考虑大幅值输入能够提高识别的模态参数精度；相比频率，模态振型精度随采样数的变化具有一定的随机性；考虑大幅值的随机子空间识别对模态试验的完备性要求较高。

桥梁工程； 模态参数； 大幅值输入； 随机子空间识别； 蒙特卡洛

引 言

模态参数识别是桥梁健康监测的一个重要组成部分。由于模态参数只取决于结构的固有属性，因此可以利用模态参数进行损伤识别、有限元模型修正和动力性能评估[1-3]。对大型桥梁和土木工程结构而言，利用环境激励进行模态参数识别(亦称工作模态识别)已经成为共识[4-7]。文献[8-10]对环境激励下模态识别的效率和精度进行了研究。近年来，环境激励的模态参数识别算法也得到进一步的完善和细化，主要体现在计算效率高、自动化程度高及识别结果准确等方面。目前，常用的环境激励模态参数识别方法包括峰值拾取法、频域分解法、时域随机子空间识别及小波分析等[11]。

尽管环境激励模态参数识别算法已经较为成熟，但是仍存在一些并非由算法本身导致的问题。文献[12]指出，目前工作模态识别存在两个主要的问题，其中之一是由于环境荷载频带窄，对结构的激励程度有限,因此只有结构低阶模态能够被识别，而对局部损伤更敏感的高阶模态难以识别。Farrar等[13]在总结桥梁结构激励方法时指出，环境激励是大型桥梁唯一切实可行的激励方法，但其缺点是不一定能激励起测试者感兴趣的频段。宗周红等[14]指出，影响有限元模型修正的一个主要问题是试验模态的不完备性，即对结构局部损伤更为敏感的高阶模态无法被环境荷载激励。文献[15]指出，对桥梁结构而言，在所有的环境荷载中，交通荷载(车辆)的强度最大，频带最宽，对结构的激励程度较高，因此可以将交通荷载视作结构的大幅值输入，从而识别部分高阶模态。文献[16]基于协方差驱动的随机子空间识别，首先将这种思想转变为现实，给出了理论解释，并通过单自由度系统数值模拟和一个高速铁路连续梁桥工作模态识别验证了这种考虑大幅值输入进行模态参数识别的可能性，但其数值模拟没有考虑识别的模态振型精度，且工程实例测试较为完备，没有考察这种方法的适用性。

笔者在文献[16]基础上，进一步利用一个两自由度系统的蒙特卡洛模拟，研究高低阶次模态随采样数和大幅值输入的变化异同，并考察大幅值输入对模态振型精度的影响。对考虑大幅值输入的随机子空间识别的适用性问题，则通过菜园坝桥拱肋脉动试验来研究。

1 理论基础

结构随机状态空间模型可以表述为

(1)

其中：yk为环境振动测试得到的结构动力响应；xk为离散状态空间的状态向量；A，C分别为状态矩阵和输出矩阵；wk，vk分别为建模误差、传感器误差与环境激励荷载之和，一般假设为白噪声。

将式(1)中的输出响应yk写成递归的表达形式

(2)

可以看到，结构的输出响应是由两个部分构成:a.结构的初始状态x0所决定，b.环境荷载wk和vk所决定。在桥梁结构动载试验中，一般会单独进行脉动试验，由于脉动荷载引起的结构振动属于微幅振动，因此式(2)中的第1项约等于0，进而利用子空间算法识别零初始状态下的系统矩阵，识别模态参数。因此，目前识别算法中并没有考虑大幅值输入对模态参数识别的影响。

在协方差驱动的子空间识别算法中，输出协方差Λi定义为

(3)

其中：N为离散采样数。

(4)

式(4)展开过程中根据互不相关白噪声特性，消去了交叉项，具体说明如下。式(1)中的wk和vk被假定为互不相关的白噪声，且其协方差为

(5)

其中：E为数学期望；δpq为克罗内克函数。

由此可以知道，当p，q不相等时，其协方差为零，即式(4)中的交叉项为零。式(4)中的第1项是由大幅值输入引起，由于初始状态为一定值，其决定的状态矩阵A和输出矩阵C亦为定值，因此，随着采样数N的增加，该项值趋近于零；第2项是由环境激励引起，根据式(3)对输出协方差的定义可知，随着N的增加，该项值逼近其真实值。根据式(4)的定性分析表明：在考虑大幅值初始状态后，当N较小时，输出协方差的精度由初始状态决定；当N趋近于无穷时，输出协方差的精度由环境荷载决定。因此，在考虑了大幅值输入之后，必然存在一个采样点数N，使得大幅值输入对输出协方差精度的影响为零。考虑大幅值输入得到协方差后，可以进一步求得系统矩阵A和C，从而求得结构的模态参数。具体流程与一般的协方差驱动的随机子空间识别相同，随机子空间算法(stochastic subspace identification,简称SSI)算法识别过程可参考文献[8]。

2 两自由度系统模拟

2.1 系统描述

文献[16]给出了一个单自由度系统考虑大幅值输入情况的蒙特卡洛数值模拟，但并没有研究大幅值输入对模态振型的影响。笔者利用一个两自由度系统数值模拟进一步考察大幅值输入对模态振型的影响。

如图1所示的两自由度系统，u(t)为白噪声环境激励，y(t)为加速度响应。令系统的质量阵M、阻尼阵C和刚度阵K分别为

计算得到该振动系统模态参数的理论解如下。

频率:f1=2.85 Hz；f2=6.97 Hz

阻尼比：ξ1=0.89%;ξ2=1.92%

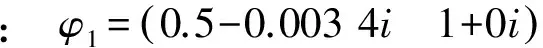
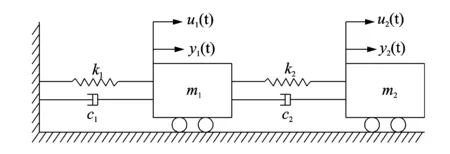
图1 两自由度系统Fig.1 2-degree of freedom system

2.2 参数设定

蒙特卡洛模拟抽样次数n取为200，环境荷载利用白噪声模拟。结构动力学中，初始状态可以是初始位移、初始速度和初始加速度，均会导致结构的自由振动。不失一般性，算例中利用初始位移来模拟大幅值初始状态的作用。初始位移仅考虑质量块m1在水平方向的位移，考虑6种不同的初始位移x0=0，0.007 5，0.015，0.025，0.035和0.045 m，对比了有无初始位移及初始位移大小对识别的模态参数的精度影响。在环境荷载和初始位移作用下质量块的加速度响应y(t)直接由随机状态空间方程递推求得，离散化时取采样频率fs=100 Hz，采样数N=18，25，26，…，216总计15种情况，再利用协方差驱动的SSI算法，采用考虑非零初始条件得到的加速度响应，识别系统的模态参数。相比有限元模拟动力响应方法，随机状态空间方程模拟方法具有效率高、误差小的优点。对200次模拟识别的模态参数求标准差以衡量其识别精度。假定一次计算响应并识别出模态参数为一个计算量，则整个计算量为200×15×6=18 000个计算量。图2给出了质量块1在初始位移为0.015 m时的自由振动响应及初始位移为0时的随机振动响应。为便于对比幅值大小，将两种响应的y坐标范围设置相同。

图2 自由振动响应和随机振动响应Fig.2 Free vibration response and ambient vibration response

2.3 结果分析

图3和图4分别为两自由度系统的频率和阻尼比相对精度随采样数的变化情况。相对精度是指利用200次模拟得到的标准差除以频率或阻尼比得到的无量纲量，该值越小，则表明多次模拟识别的模态频率和阻尼比稳定性越高，可信程度更高。图5为模态振型的精度随采样数的变化。

首先，观察频率的相对精度变化情况。从图3可以看出：

图3 不同初始位移下频率相对精度随采样数的变化Fig.3 The relative accuracy of frequencies with data samples under different initial displacements

1) 初始条件为0的曲线一直呈现下降趋势，表明随着采样数的增加，输出协方差逐渐逼近其真实值，频率识别精度越高；

2) 对初始位移不为0的曲线，从斜率可以看出，曲线下降的趋势经历快、慢、快3个过程，对初始位移较大的情况，甚至出现反弯点(如初始位移为0.035 m的曲线，采样数为104对应的点即为反弯点)，这与理论推导中的定性分析结果一致，表明在拐点处初始位移的影响逐渐趋于零，环境荷载起主导作用；

3) 在相同的采样数下，初始位移越大，识别的频率精度越高，表明大幅值的初始位移能够提高模态频率的识别精度；

4) 无论是零初始位移还是非零初始位移曲线，当采样数大到一定程度时，频率的精度提升不明显。

以上几点在图4和图5中也有所体现。

其次，观察第1阶模态和第2阶模态识别精度随采样数N的变化情况，对比图3～图5中的(a)和(b)图，可以看出：

图4 不同初始位移下阻尼比相对精度随采样数的变化Fig.4 The relative accuracy of damping ratios with data samples under different initial displacements

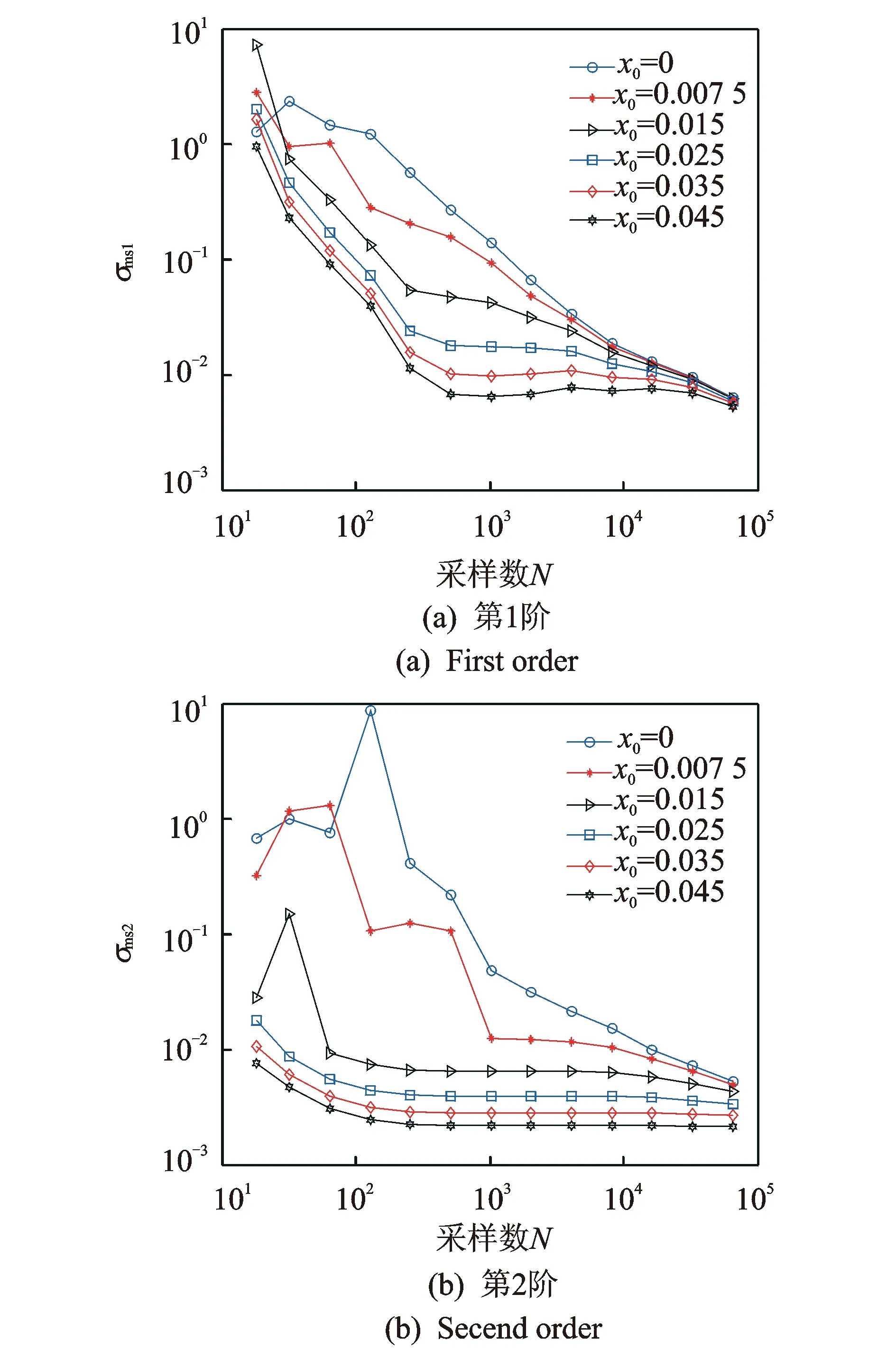
图5 不同初始位移下模态振型精度随采样数的变化Fig.5 The accuracy of mode shapes with data samples under different initial displacements

1) 第2阶模态参数精度随采样数增加会出现一个明显提升点(反映在曲线上突降点)，其后也呈现与第1阶模态参数相同的变化规律，这表明相对高阶次的模态参数精度对采样数更为敏感；

2) 在曲线的末尾段，模态1比模态2更为聚拢，表明要是不同初始位移下识别的模态参数达到同样精度，高阶次模态需要更多的采样数；

3) 在较低的采样数下，高阶次模态对应的曲线图无变化规律，甚至在图4(b)和图5(b)中，零初始位移曲线有些跳点呈现上升趋势，这表明对高阶模态而言，在采样数较少时，无法用理论分析结果来预测其精度水平。

最后，对比频率、阻尼比和模态振型的识别结果可以发现，不同初始位移的频率精度随采样数的变化曲线最能体现理论分析的结果，而阻尼比和振型的精度变化出现更多的随机性。这也反映了目前工作模态分析中常见的现象，即频率识别精度较高，而阻尼比和振型的识别精度难以控制，尤其是阻尼比，识别的结果呈现较大的离散性。

3 菜园坝桥拱肋模态参数识别

文献[16]通过一个测试完备的连续梁桥的工程实例得到了如下结论：a.考虑大幅值输入后，识别的模态参数精度有所提高；b.考虑大幅值输入后，能够识别一些结构的高阶模态。笔者通过菜园坝长江拱肋脉动试验进一步研究考虑大幅值输入的随机子空间识别方法的适用性。

3.1 试验介绍

菜园坝长江大桥主桥为主跨420 m的钢桁梁、钢箱系杆拱组合结构。拱肋脉动试验是全桥荷载试验的一部分，旨在了解其结构固有振动特性。全桥荷载试验包括主桥和引桥静载试验和动载试验。脉动试验对主桥桥面和拱肋分别进行单独测试，这里选取上游侧拱肋脉动试验数据进行分析。对拱肋进行脉动试验时，测试其无车状态下在环境荷载作用下的加速度响应。测试利用2个941B加速度拾振器完成，一个作为参考点传感器，另一个作为移动传感器。拱肋共布置19个测点，测点均位于吊杆处。测点布置如图6所示，分18个测试组完成，每个测试组采样时间约3～5 min，采样频率为20 Hz。

由于脉动试验全过程无车过桥，而环境荷载引起的桥梁振动属于微幅振动，因此可以将脉动试验下桥梁动力响应视作零初始状态下振动响应。相比环境荷载，车辆荷载频带较宽，对桥梁引起的振动也不可忽视，因此将车辆荷载引起的桥梁自由振动响应视作桥梁处于大幅值状态下的振动响应。

从上面的试验描述可知，拱肋的脉动试验测试相对简易，重点考察考虑大幅值输入的随机子空间识别对这种测试不够完备的情况适用性。

图6 测点布置图Fig.6 The layout of measuring points

3.2 结果分析

图7和图8分别是利用脉动试验响应(无大幅值输入)和行车试验数据(有大幅值输入)计算得到的稳定图，图中“.f”，“.d”和“.v”分别表示频率、阻尼比和模态振型向量的稳定点，而圆圈十字表示三者共同的稳定点。频率、阻尼比和振型的稳定准则分别为相邻两阶的容差不超过1%，5%和1%。

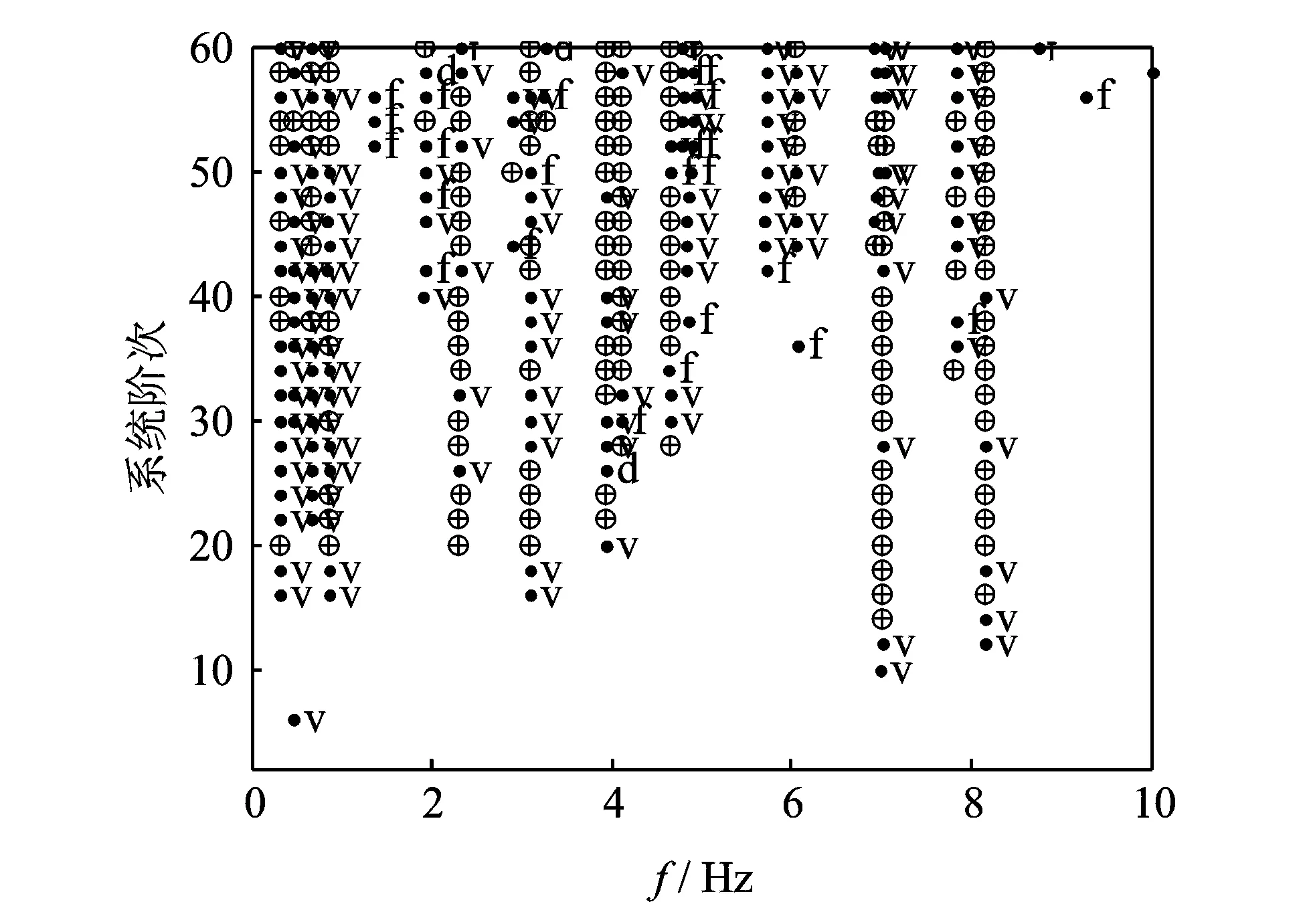
图7 利用脉动试验数据提取的稳定图Fig.7 The stabilization diagram extracted from ambient vibration test

图8 利用行车试验数据提取的稳定图Fig.8 The stabilization diagram extracted from driving test

对比两图可以看出：

1) 在0～2 Hz范围内，考虑大幅值后得到的稳定图显示更多的稳定点，稳定轴更为清晰；

2) 在6～8 Hz范围内，考虑大幅值后的稳定图明显少了一个清晰的稳定轴，即产生了模态遗漏。

将识别的拱肋前6阶模态频率和阻尼比列入表1，对比可以发现，二者识别的阻尼比较为离散，但频率基本一致，且考虑大幅值输入后识别的模态频率偏大。

表1 拱肋前6阶频率和阻尼比

Tab.1 The frequencies and damping ratios of first six modes of arch rib

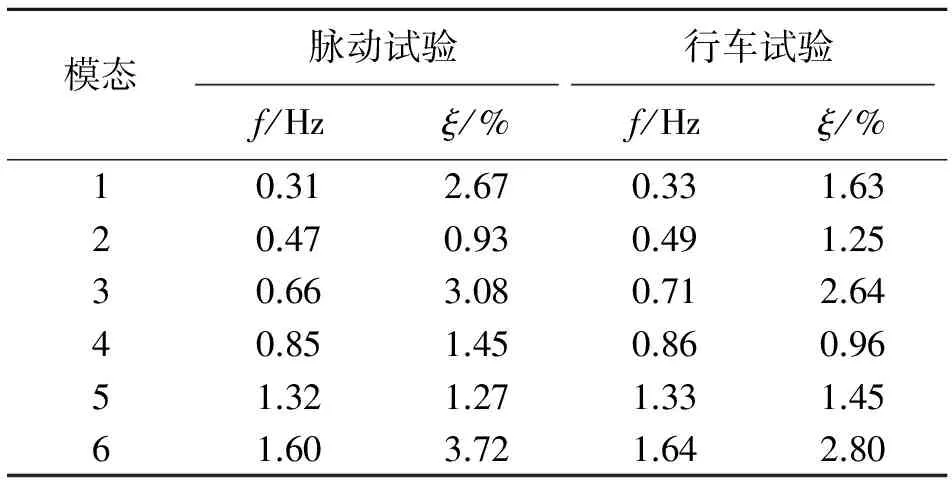
模态脉动试验行车试验f/Hzξ/%f/Hzξ/%10．312．670．331．6320．470．930．491．2530．663．080．712．6440．851．450．860．9651．321．271．331．4561．603．721．642．80

从试验结果可以看出，在测试相对简易的情况下，考虑大幅值输入的随机子空间识别并没有达到识别高阶模态和提高识别精度的目的，与理论分析和数值模拟有所差异。这表明，考虑大幅值输入的随机子空识别对测试的完备性要求较高，限于各个工程不同以及测试过程所用仪器等差异，无法给出一个模态试验完备与否的明确区分标准。文献[7]指出，根据过往工程经验，在采样频率为100 Hz，采样时间为960 s左右时能够较准确识别桥梁结构的模态参数(包括模态振型)，同时还需要考虑移动传感器的时间来保障测试的完备性。

4 结 论

1) 考虑大幅值输入后，输出协方差由两部分组成:a.由大幅值输入决定；b.由环境荷载决定。二者的精度随采样数变化成反比，即存在一个采样数，使得大幅值对输出协方差的影响为零。

2) 数值模拟表明，考虑大幅值输入后识别的模态参数精度得到提高，且输入幅值越大，精度提高程度越高。模态振型的变化规律与频率相仿，但存在更多的随机性。

3) 试验研究表明，考虑大幅值输入的随机子空间识别对测试的完备性要求较高，当测试完备性较低时，考虑大幅值的识别方法不能达到理论推导和数值模拟的效果。

4) 目前仍无法给出一个测试完备性与否的评判标准，但可以参考现有研究对环境振动测试能够准确识别结构的模态参数所设置的标准。

[1] Reynders E, Teughels A, DeRoeck G. Finite element model updating and structural damage identification using OMAX data[J]. Mechanical Systems and Signal Processing， 2010,24(5):1306-1323.

[2] Magalhães F, Cunha A, Caetano E. Vibration based structural health monitoring of an arch bridge: from automated OMA to damage detection[J]. Mechanical Systems and Signal Processing， 2012,28(2):212-228.

[3] 刘雨青. 桥梁结构模态参数识别与应用研究[D]. 武汉：武汉理工大学, 2005.

[4] 闵志华，孙利民，孙智，等. 环境激励下基于小波变换和奇异值分解的结构模态参数识别[J]. 振动工程学报， 2009(2):142-149.

Min Zhihua, Sun Limin, Sun Zhi, et al. Structural modal parameter identification using wavelet transform and singular value decomposition under ambient excitation[J]. Journal of Vibration Engineering， 2009(2):142-149. (in Chinese)

[5] Brownjohn J M W, Magalhaes F, Caetano E, et al. Ambient vibration re-testing and operational modal analysis of the Humber Bridge[J]. Engineering Structures, 2010,32(8):2003-2018.

[6] 蒲黔辉，秦世强，施洲，等. 环境激励下钢筋混凝土拱桥模态参数识别[J]. 西南交通大学学报. 2012,47(4):539-545.

Pu Qianhui, Qin Shiqiang, Shi Zhou, et al. Modal parameter identification of reinforced concrete arch bridge under ambient excitation[J]. Journal of Southwest Jiaotong University, 2012,47(4):539-545.(in Chinese)

[7] Magalhöes F, Caetano E, Cunha, et al. Ambient and free vibration tests of the millau viaduct: evaluation of alternative processing strategies[J]. Engineering Structures, 2012,45(15):372-384.

[8] Peeters B, De Roeck G. Reference-based stochastic subspace identification for output-only modal analysis[J]. Mechanical Systemand Signal Processing, 1999,13(6):855-878.

[9] 叶锡钧，颜全胜，王卫锋，等. 基于多参考点稳定图的斜拉桥模态参数识别[J]. 华南理工大学学报:自然科学版, 2011,39(9):41-47.

Ye Xijun, Yan Quansheng, Wang Weifeng, et al. Modal parameter identification of cable-stayed bridge based on multiple references DOFs stabilization diagram[J]. Journal of South China University of Technology:Natural Science Edition,2011,39(9):41-47. (in Chinese)

[10]Ren Wwixin, Peng Xuelin, Lin Youqin. Experimental and analytical studies on dynamic characteristics of a large span cable-stayed bridge[J]. Engineering Structrues, 2005,27(4):535-548.

[11]谢旭，吴冬雁，张鹤，等. 运营条件下异型拱桥的模态参数识别[J]. 振动、测试与诊断, 2014,34(6):989-994.

Xie Xu, Wu Dongyan, Zhang He, et al. Operational modal parameter identification of irregular arch bridge[J]. Journal of Vibration, Measurements & Diagnosis, 2014,34(6):989-994. (in Chinese)

[12]Reynders E, De Roeck G. Reference-based combined deterministic-stochastic subspace identification for experimental and operational modal analysis[J]. Mechanical Systems and Signal Processing, 2008,22(3):617-637.

[13]Farrar C R, Duffey T, Cornwell P J, et al. Excitation methods for bridge structures[C]∥17th InternationalModal Analysis Conference． Florida:Society for Experimental Mechanics,Inc, 1999.

[14]宗周红，任伟新. 桥梁有限元模型修正和模型确认[M]. 北京：人民交通出版社，2012:4-8.

[15]秦权. 桥梁结构的健康监测[J]. 中国公路学报, 2000,13(2):39-44.

Qin Quan. Health monitoring of long-span bridges[J]. China Journal of Highway and Transport, 2000,13(2):39-44. (in Chinese)

[16]Qin Shiqiang, Reynders E, He Leqia, et al. Effects of initial conditions in operational modal analysis[J]. Structural Control and Health Monitoring, 2014,21(4), 557-573.

10.16450/j.cnki.issn.1004-6801.2016.06.009

*国家自然科学基金资助项目(51608408)；中央高校基本科研业务专项资金资助项目(WUT-2014-IV-047)

2014-11-26；

2015-03-03

TU311

秦世强，男，1987年7月生，博士、副教授。主要研究方向为桥梁健康监测、结构动力学系统识别。曾发表《Effects of initial conditions in operational modal analysis》(《Structural Control and Health Monitoring》2014,Vol.24,No.4)等论文。 E-mail：shiqiangqin@163.com