风机叶片疲劳加载振动频率特性分析与试验*

2017-01-09廖高华乌建中张磊安

振动、测试与诊断 2016年6期

关键词：偏心振幅驱动

廖高华，乌建中，张磊安

(1.同济大学机械与能源工程学院上海，201804)(2.南昌工程学院江西省精密驱动与控制重点实验室南昌，330099)

风机叶片疲劳加载振动频率特性分析与试验*

廖高华1,2，乌建中1，张磊安1

(1.同济大学机械与能源工程学院上海，201804)(2.南昌工程学院江西省精密驱动与控制重点实验室南昌，330099)

针对风机叶片疲劳加载过程振动特性，建立旋转偏心块驱动的叶片疲劳加载系统动力学模型。基于拉格朗日方程推导出系统的数学模型，利用平均法近似解析系统动力学方程，得出振动过程中电机转矩平衡方程。分析振动频率的变化规律，建立仿真模型，对系统频率捕获过程进行数值仿真，揭示系统的自同步振动特性。风机叶片疲劳加载试验表明：叶片在受迫振动时，叶片振动频率并不总等于驱动频率；驱动频率与叶片固有频率偏差较大时，叶片振动幅值及频率波动明显；频率偏差在较小区间范围(0.47～0.62 Hz)时，偏心块驱动系统与叶片容易发生频率捕获，振幅较小并趋于稳定；在负载转矩较大而电机功率不足时，偏心块会发生转速跳变。

疲劳试验；风机叶片；耦合；频率特性；仿真

引言

叶片是风力发电机组的关键部件，风力机叶片大部分采用玻璃纤维复合材料，叶片疲劳检测是认证程序的基本部分，其目的在于确定叶片的疲劳寿命[1]。国际上风电技术研究发达国家的相关科研机构大都建有大型叶片检测平台，开展叶片试验研究工作。疲劳加载试验目前主要采用偏心块共振加载和液压缸强迫加载模式。偏心块共振加载模式在相同振幅下，能耗小于强迫加载模式能耗，能有效减少试验时间，节省能量，具有设备成本低等优点。国内上海玻璃钢研究院、中科院工程热物理研究所等单位采用偏心块共振加载模式进行疲劳加载试验[2-3]。风机叶片激振加载时，系统加载过程存在较强的耦合作用，小幅度外部激励会产生很大的响应，激振频率特性对叶片疲劳加载系统的性能和效率影响很大。国内外学者采用软件分析与数值计算方法对风力机叶片疲劳性能及动力学[4-5]进行了研究。文献[6]通过推导出叶片的耦合动力学混合有限元模型，以某1.5MW叶片求解其自由振动力学结果。文献[7-8]用试验方法对小型风力机叶片进行疲劳特性分析，但主要是围绕激振振幅与振动次数的关系以及振动原理进行探讨。文献[9-10]对双转子电机振动耦合特性进行分析，对振动及其频率捕获进行了定量研究，得到电机趋于自同步过程中参量的变化规律。

笔者针对风机叶片面向旋转偏心块疲劳加载系统，建立系统的动力学模型，对动力方程进行了近似解析，分析了系统的振动频率特性，进行了数值仿真，并利用风机叶片疲劳加载试验进行验证，为风机叶片疲劳共振加载试验提供一定的理论依据。

1 疲劳加载系统数学模型

叶片疲劳加载系统包括支撑系统、动力传动系统、检测控制系统和保障系统，如图1所示。离心力作为激振力对叶片做功，通过减速电机带动偏心块在竖直平面内作近似正弦转动，偏心块以接近叶片固有频率的激振频率转动，使叶片发生共振。通过调整质量块大小，可以使叶片达到试验要求的振幅。激光测距仪在疲劳试验时监测叶片振幅的变化，可编程逻辑控制器(programmable logic controller,简称PLC)控制变频器，调整电机输出转速，使得偏心块转动频率为叶片1阶弯曲振动共振频率。

图1 面向旋转偏心块疲劳加载系统Fig.1 Rotating fatigue loading system

对叶片疲劳加载系统，偏心块转动产生激振力使叶片振动，表现水平x、垂直y方向以及扭转方向φ运动。根据文献[11]，系统建模时作了如下合理假设：a.叶片近似为线性弹性体，在振动过程中受到弹性力及阻尼力作用，叶片黏性阻尼起主要作用，叶片竖直方向的弹性力和阻尼力分别为位移和速度线性函数；b.加载源与连接夹具均为均质刚体。在上述假设前提下，建立加载系统动力学模型，如图2所示。

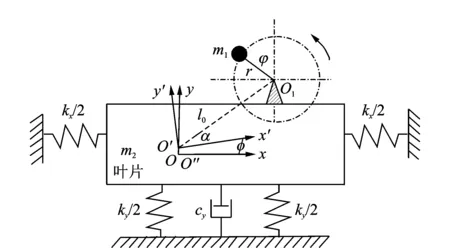
图2 叶片疲劳加载力学模型Fig.2 Mechanical model of fatigue loading

选择叶片运动坐标x，y及偏心块旋转相位φ为广义坐标，O′与O为叶片与偏心块合成质心，O″为叶片质心，Oxy为固定坐标，O′x′y′为动坐标，O1O′=l0。利用拉格朗日方程推导方程式，得到叶片3个方向的动力学方程为

(1)

其中：x，y，φ分别为水平、垂直及扭转方向的位移；m1，m，r，φ分别为偏心块质量、系统总质量、偏心距及角位移；cx，cy，cφ分别为x，y及φ方向的阻尼系数；kx，ky及kφ分别为x，y及φ方向的刚度系数；J1，c1为偏心块绕O1点转动惯量与回转阻尼系数；J为叶片绕O1点转动惯量；Tf为负载等效为转矩；Tm为驱动系统对叶片的作用等效为转轴上施加恒定转矩。

加载系统选用三相异步耐振电动机及二相同步旋转坐标系下数学模型，其状态方程[12]可表示为

(3)

其中：Udr,Uqr为转子端电压；Uds,Uqs为定子端电压；Idr,Iqr为转子端电流；Ids,Iqs为定子端电流；Ls,Lr分别为定、转子自感；Lm为定、转子互感；Rs,Rr分别为定、转子电阻；ω1,ωr分别为同步旋转角速度和转子角速度；J为机组转动惯量；D为摩擦及风阻力矩系数。

式(1)～式(3)构成了疲劳加载系统振动耦合数学模型。从模型上看是一个多变量耦合的非线性系统，加载装置与叶片运动之间存在着相互耦合关系。

2 振动耦合近似解析

加载系统动力学方程(1)为非线性微分方程组，一般很难求解出其精确解析解。为了简化问题，假设偏心块加载装置中垂线在叶片质心上，采用平均法对系统动力学方程进行近似解析，得到振动过程中电机转矩平衡方程，分析振动频率的变化规律。对于叶片垂直振动方向，可得

(4)

由于偏心块质量m1相对叶片质量m2是小量，式(4)可表示为

(5)

设φ=Ωt+c+εW(t)，W(t)为周期函数，式(5)可变成拟线性方程形式

(6)

假设式(6)的解的形式为

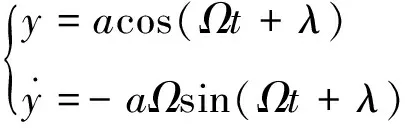
(7)

由平均法得到的标准方程为

(8)

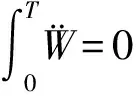
(9)

对标准方程式(8)，a与λ是t的缓变函数，一般具有非线性。为了进行近似求解，将a与λ写成平稳项e，λ和小变化量叠加，利用克雷洛夫-包戈留包夫变换(KB变换)得

(10)

(11)

其中：U(t,e,ϑ)，V(t,e,ϑ)为周期函数(周期为T)；e，ϑ，Y1，Y2，Z1，Z2不显含t。

经运算得到Y1与Z1的表达式，代入式(11)并化简可得

(12)

当共振时，令式(12)等于零，可得方程的定常解

(13)

结合式(9)可得

(14)

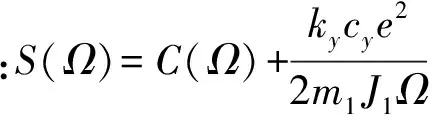
式(14)为偏心块驱动加载系统的转矩平衡方程，反映了在激振过程中负载与动力系统之间的关系。由式(14)得到S(Ω)曲线，结合电机的T(Ω)曲线，其交点为转矩平衡方程的解，如图3所示。静力矩曲线ti右移，激振频率增大，电机需求功率增大。当到达曲线t3位置时，此时振动系统的激振频率会从c1点快速跳变到c2点，振幅迅速变小。继续加大电机的转速，振动体的激振频率进入平稳区。同理，当激振频率减小时会出现从a2到a1的频率跳变。根据能量最小及稳定性原理，稳定性条件d[T(Ω)-C(Ω)]/dΩ<0，c1到a2区间内的激振频率满足稳定条件，但不能实现，在整个激振频率区域会出现不连续段。如果电机额定功率足够大，即静力曲线ti的倾斜达到一定程度，不连续区域将缩小甚至消除，而电机功率较小时，将出现跳变现象。由式(14)可知：当振幅最大时具有最大的负载转矩，此时容易发生频率跳变；当振动系统具有较小的阻尼比时，固有频率点即为频率最容易跳变点；当阻尼比较大时频率跳变点位于固有频率的右端。

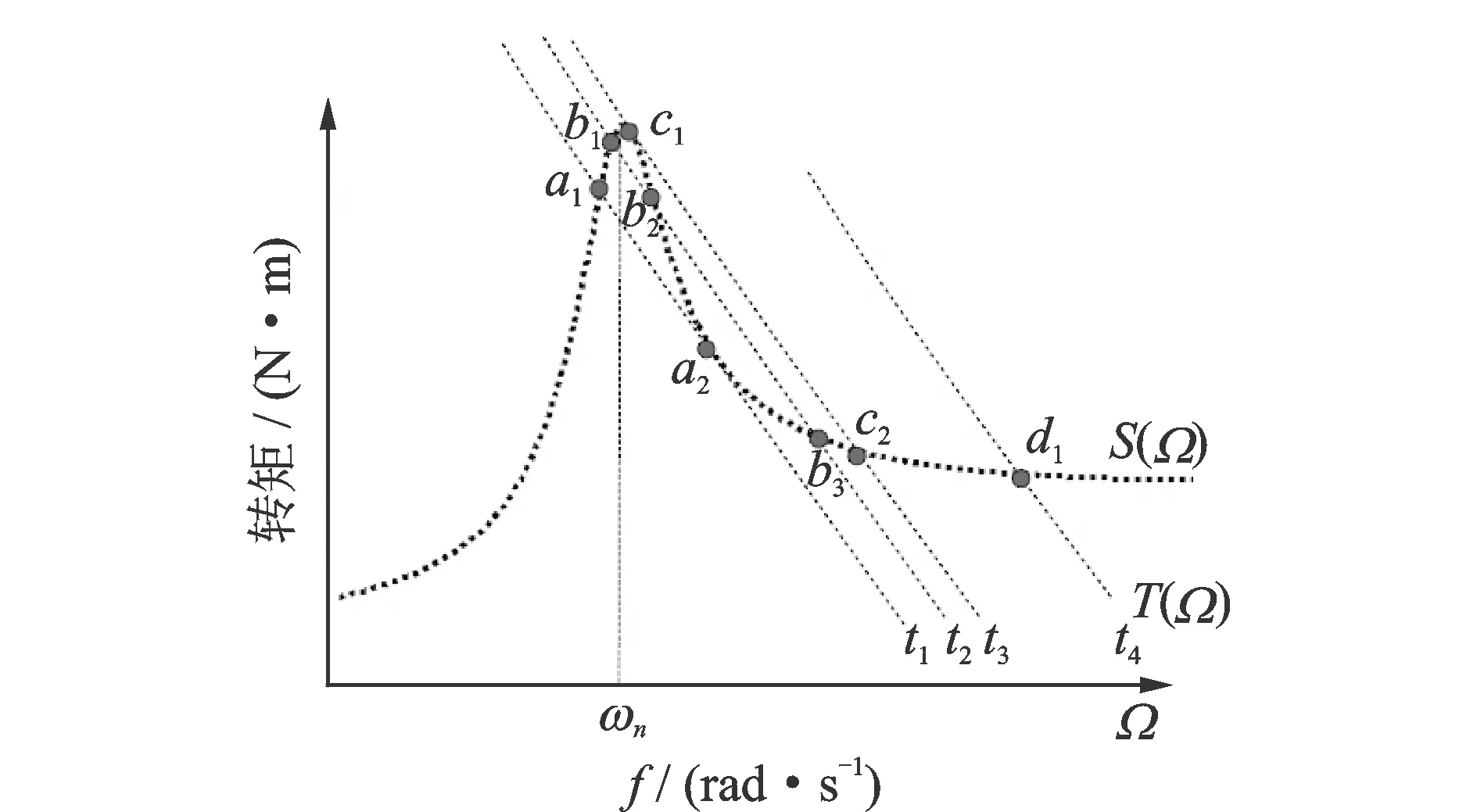
图3 振动系统的S-T曲线Fig.3 S-T curves of excitation system

3 振动频率捕获仿真分析

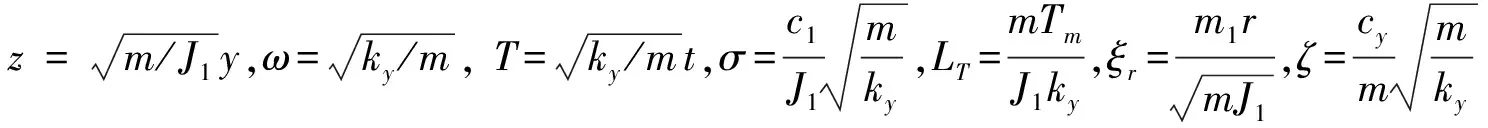
(15)

其中：z′，z″为参数T的1阶、2阶微分；ζ，σ数值较小，近似认为0。

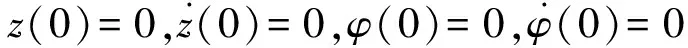
固定无量纲参数LT，改变参数ξr数值仿真，如图4所示。从图4(a)频率俘获仿真曲线可看出，z方向位移随着偏心块角速度增大而增大。当到达155 s时，在共振点ω=1附近振荡，角速度不再增加(保持近似不变)，驱动系统与叶片“同步”，位移逐渐增大，并最终维持稳定。从图4(b)频率俘获曲线可看出，随着偏心块角速度递增，在振幅最大时速度相对最小，振幅与最大速度的相位差为π/2。当到达155 s时，偏心块角速度曲线出现一段水平，z方向振幅最大，角速度继续增大，z方向振幅却逐渐变小，并最终趋于稳定。

图4 频率仿真曲线1Fig.4 Frequency acquisition simulation curve 1

固定参数ξr，改变LT数值仿真，如图5所示。从图5(a)频率俘获曲线可以看出，起振轨迹与图4中结果一致，振幅、速度逐渐增大，且相位差π/2。当到达235 s时，偏心块角速度出现了一段水平，z方向振幅最大。虽然偏心块角速度继续增大，但z方向振幅却变小，最终趋于稳定。从图5(b) 频率俘获曲线可看出，当到达270 s时，偏心块角速度不再增加，驱动系统与叶片发生“同步”，但振幅却在逐渐增大。

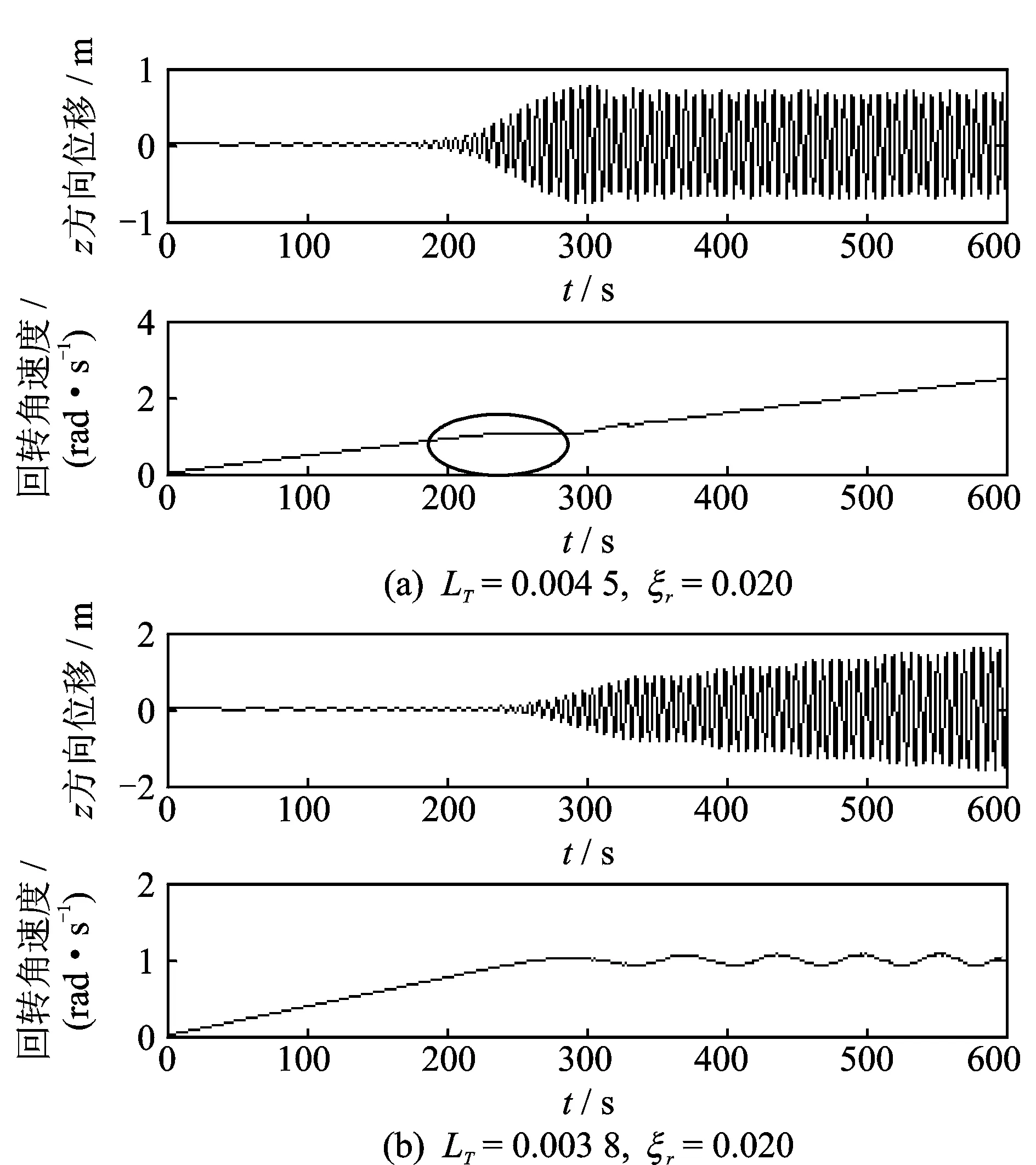
图5 频率仿真曲线2Fig.5 Frequency acquisition simulation curve 2

由上述可知，当参数LT= 0.007 5，ξr≥0.029 时，系统振动会发生频率俘获；当参数ξr= 0.02，LT≤0.004 5时，振动会发生频率俘获。频率捕获依赖于初始条件与系统参数，在电机功率一定时，摆臂长及偏心块质量越大，则越容易发生频率捕获。

4 疲劳试验与分析

将风机叶片根部固定在加载支座上，在距离叶片根部70%处夹具上固定偏心块加载装置，叶片试验现场如图6所示。激光测距仪实时监控叶片加载点位移，采集系统接收实测数据。变频器无级调速，根据叶片状态调整变频器，扫描捕捉系统共振点，实现叶片共振并维持振幅恒定。试验中记录测试数据，包括电机转速、摆臂转动频率、叶片振动频率及振幅等参数。

图6 疲劳加载试验现场Fig.6 Fatigue loading test site

叶片低阶固有频率(0.56 Hz)，采用不同驱动频率对风电叶片进行多次疲劳加载试验，频率扫描搜索过程曲线如图7所示。叶片在受迫振动时，叶片振动频率并不总等于激振频率。在低频时，叶片振动频率不等于激振频率；当激振频率大于某个值时，叶片振动频率基本趋近于激振频率。

图7 频率扫描搜索过程曲线Fig.7 Frequency scanning search process curve

当频率在0.47～0.62 Hz区间时，叶片振动频率跟随着偏心块驱动频率变化，发生了频率捕获，叶片振幅曲线如图8所示。当偏心块驱动频率为0.47 Hz时，叶片振幅经波动较大之后逐渐趋于平稳。当叶片振幅稳定后，振动频率与偏心块驱动频率基本一致，叶片振幅比较小，维持在110 mm左右，驱动的能量耗散在频率捕获过程。偏心块驱动频率为0.62 Hz，叶片振幅在波动较大之后，逐渐趋于稳定，此时其振动频率已偏离其固有频率。叶片振动频率与偏心块驱动频率相一致，叶片振幅维持在310 mm左右。

当偏心块驱动频率小于0.43 Hz或大于0.67 Hz时，叶片的振动频率不易被捕获，叶片振动频率在一定范围内波动。偏心块驱动频率离叶片的频率捕获区间越远，叶片振动频率波动越明显，振动幅值也越小。当控制变频器使偏心块转速为35 r/min时，偏心块回转驱动频率略大于叶片固有频率，此时具有较大振幅和负载转矩，偏心块转速发生了转速跳变。偏心块转速及叶片峰值波动曲线如图9所示。

图8 叶片振幅及频谱曲线Fig.8 Blade amplitude and spectrum curve

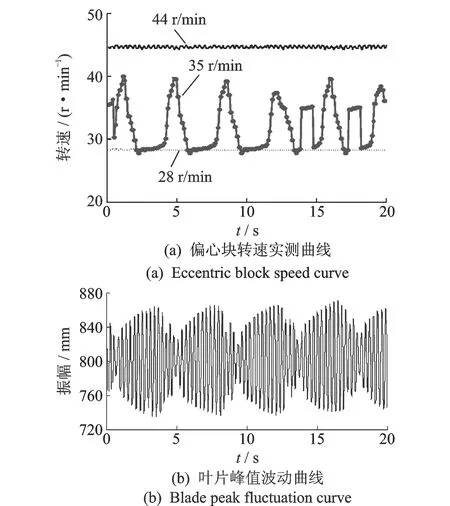
图9 偏心块转速及叶片峰值波动曲线Fig.9 Eccentric block speed and blade amplitude peak curve

5 结论

1) 建立偏心块驱动的风机叶片疲劳加载系统动力学模型，得到加载系统的负载平衡方程，分析了系统振动耦合特性。系统的激振频率不仅受振动系统的阻尼及振幅等振动状态、外负载等因素相互影响，还与动力系统特性相关。有限功率下激振过程会出现频率跳变，频率跳变是电机功率不足的结果，频率跳变点与阻尼比相关，跳变点一般出现在加速度共振点。

2) 仿真试验表明，系统频率捕获依赖于初始条件与系统参数。电机扭矩越大，越不容易发生频率捕获。但在频率捕获区间内，电机扭矩越大，频率捕获的时刻提前，叶片幅值相应增大。在电机功率一定时，摆臂长及偏心块质量越大，越容易发生频率捕获。

3) 叶片振动频率并不总等于激振频率。偏心块驱动频率与叶片固有频率偏差较大时，叶片振动幅值及频率波动明显；当频率偏差较小时，偏心块驱动系统与叶片会发生频率捕获，表现为叶片振动频率与驱动频率趋近一致，叶片的振幅会维持稳定。

[1] Malhotra P, Hyers R W, Manwell J F, et al. A review and design study of blade testing system for utility-scale wind turbines[J].Renew Sustain Energy Reviews, 2012,16(1):284-292.

[2] 张磊安，黄雪梅，王娜，等.风电叶片单点疲劳加载过程数值仿真与试验[J].振动、测试与诊断，2014,34(4):732-736.

Zhang Leian, Huang Xuemei, Wang Na, et al. Numerical simulation and test on MW wind turbine blade single fatigue loading process[J]. Journal of Vibration, Measurement & Diagnosis，2014,34(4):732-736. (in Chinese)

[3] 石可重，赵晓路，徐建中. 大型风电机组叶片疲劳试验研究[J]. 太阳能学报，2011，32(8): 1264-1268.

Shi Kezhong, Zhao Xiaolu, Xu Jianzhong. Research on fatigue test of large horizontal axis wind turbine blade[J]. Acta Energiae Solaris Sinica,2011,32(8): 1264-1268. (in Chinese)

[4] 陈严，张林伟，刘雄，等. 水平轴风力机叶片疲劳载荷的计算分析[J]. 太阳能学报，2013，34(5): 902-908.

Chen Yan,Zhang Linwei,Liu Xiong, et al. Fatigue load calculation and analsis of the blade of horizontal aixis wind turbine[J]. Acta Energiae Solaris Sinica,2013,34(5): 902-908. (in Chinese)

[5] Nitin T. Design and finite element analysis of horizontal axis wind turbine blade[J].International Journal of Applied Engineering Research, 2010(1):500-507.

[6] 王建礼，石可重，廖猜猜，等.风力机叶片耦合振动力学模拟及实验研究[J]. 工程热物理学报, 2013,34(1):67-70.

Wang Jianli,Shi Kezhong, Liao Caicai, et al.Study on coupled vibration simulation and experiment of wind turbine blade[J]. Journal of Engineering Thermophysics, 2013, 34(1):67-70. (in Chinese)

[7] 单光坤，关新，宋世东．100 kW风力发电机叶片疲劳分析[J]. 可再生能源, 2010,28 (2):21-26.

Shan Guangkun, Guan Xin, Song Shidong. Fatigue analysis on blade of 100 kW wind turbine[J]. Renewable Energy Resources, 2010,28 (2):21-26. (in Chinese)

[8] 萨昊亮，李成良，余启明，等. 风电叶片疲劳试验振动分析与研究[J]．玻璃钢/复合材料，2013(2):57-59.

Sa Haoliang，Li Chengliang，Yu Qiming，et al. Analysis and research on dynamic test of wind turbine rotor blade[J]．Fiber Reinforced Plastics/Composites，2013(2):57-59. (in Chinese)

[9] Zhao Cunyu, Zhang Yimin, Wen Bangchun, et al. Synch ronizat ion of two non-ident ical coupled ex citers in a non- resonant vibrating system of plane motion[J]. Journal of Mechanical Science and Technology, 2011, 25(1):49-60.

[10]王得刚，赵清华，赵春雨，等.同向回转双机驱动振动系统的自同步特性[J].振动、测试与诊断，2010,30(3):217-222.

Wang Degang, Zhao Qinghua, Zhao Cunyu, et al. Self synchronous feature of a vibrating system driven by two motors with the same rotation direction[J]. Journal of Vibration, Measurement & Diagnosis，2010, 30(3):217-222. (in Chinese)

[11]William M H. The development of an adaptive control system for a phase locked excitation (PhLEX) method for advanced wind turbine blade fatigue testing[D]. Daytona Beach:Embry-Riddle Aeronautical University, 2010.

[12]王锋，姜建国，颜天佑. 基于Matlab 的异步电动机建模方法的研究[J]. 系统仿真学报，2006 ,18(7) :1733-1741.

Wang Feng, Jiang Jianguo,Yan Tianyou. Methods of asynchronous motor model simulation based on Matlab[J]. Journal of System Simulation, 2006,18(7): 1733-1741. (in Chinese)