响应面法用于磨机传动系统扭转振动模型修正*

2017-01-09郭勤涛

振动、测试与诊断 2016年6期

关键词：磨机传动系统修正

陶征，刘旭，郭勤涛

(1.郑州大学机械工程学院郑州，450001) (2.南京航空航天大学机电学院南京，210016)

响应面法用于磨机传动系统扭转振动模型修正*

陶征1，刘旭1，郭勤涛2

(1.郑州大学机械工程学院郑州，450001) (2.南京航空航天大学机电学院南京，210016)

大型设备传动系统的扭转振动影响系统的正常工作，严重时会导致系统损坏，避免共振是缓解扭转振动的有效手段，针对此问题，以某大型磨机设备为研究对象，建立以响应面法的有限元模型修正理论为基础的方法。通过扭转振动分析，经显著参数筛选，以显式的响应面模型逼近特征量与设计参数间复杂的隐式函数，对传动系统有限元模型可能存在的误差进行修正。在获得较精确模型的基础上，对其传动系统进行了基于响应面的优化设计，调整系统的模态频率，使其有效避开了系统的工作频率，实现了传动系统的优化，表明以响应面法的有限元模型修正方法对传动系统设计具有参考价值。

传动系统；响应面法；模型修正；扭转振动

引言

随着机械工业技术的进步，机械设备的设计水平在不断提高，其传动系统也越来越复杂。如果传动系统设计不合理，就有可能使机械传动系统产生较大的扭转振动而损坏，使机械设备无法正常工作，甚至出现严重后果。美国马凯德水泥厂就曾经因为传动系统设计的不合理使其所用的设备产生共振[1]。重庆地维水泥公司的球磨机传动系统也出现过剧烈的振动现象[2]。

基于有限元模型修正的方法对传动系统扭转振动的动力学特性进行分析，成为优化设计、提高机械设备整体动态性能的一个基本方法。基于响应面的有限元模型修正方法是近年来有限元模型修正技术新的研究方向[3-6]，其以显式的响应面模型逼近特征量与设计参数间复杂的隐式函数关系，可以更好地解决传动系统中存在的不确定参数这一问题，同时修正过程运行快、效率高。

笔者针对某大型磨机在设计过程中要求避免产生共振的问题，首先，通过建立其传动系统的有限元模型，以实际磨机的固有频率为目标，基于响应面法对其有限元模型进行了模型修正，获得精度较高的有限元模型；然后，通过坎贝尔图确定系统共振频率的半功率共振区，进而对有限元模型进行新的目标参数优化，从而使得在新的设计参数下的磨机系统共振频率有效的避开了主要工作频率，最终达到了解决磨机在工作过程中产生共振问题的目的。

1 理论基础

基于响应面的有限元修正法包含的理论基础主要有试验设计、参数筛选、响应面拟合及参数修正[7-8]。

1.1 显著性参数筛选

响应面的输入参数应是具有对特征量有显著影响的设计参数。显著参数的筛选方法是以试验设计为基础，在参数的设计空间内确定样本点，利用样本点进行有限元分析计算获得样本值，并对其进行方差分析，进而达到确定影响系统特性的显著性参数的目的。笔者以模态频率为指标，挑选显著参数作为待修正对象。

常用的试验设计方法有D-最优设计、正交设计、均匀设计、拉丁方设计及中心复合设计等[9]。运用正交设计方法和均匀设计方法拟合低阶模型可获得良好的精度，同时它们还具有直接通过表格设计的简单高效的特点，所以笔者采用正交设计和均匀设计相结合的方法，来进行参数的筛选和响应面拟合。

方差分析用于检验因素是否显著影响试验结果。其基本思想是计算由各个因素引起的离差平方和及由误差引起的离差平方和，然后除以各自的自由度，求出它们的比值(F值)进行假设检验。假设对有限元模型的设计参数X(因素)进行F检验，统计量则为

(1)

其中：SX，SE分别为因素和误差的离差平方和；fX，fE分别为因素和误差的自由度。

1.2 响应面拟合

在有限元模型修正中，通常以二次多项式作为响应函数，其表达的曲面即为响应面。假设系统的特征量y为因变量，设计参数为xi，i=1，2，…，k，含交互项的二次多项式响应函数形式为

(2)

若样本点不足，可以通过试验设计增加新的样本点，进而在有限元模型中计算样本值，然后将所有样本数据代入式(2)，通过最小二乘法获得系数β的估计

(3)

解式(3)可得β值，即得到响应面函数表达式。为进一步提高响应面的精度，采用了含交互项的三次多项式作为响应函数。根据下列公式进行响应面精度检验

R2值表示响应面模型与有限元模型之间的差异程度，值越大，二者差异越小。RMSE的值与R2值相反。若检验后的精度不符合要求，则需要增加样本点数。

1.3 参数修正

有限元模型修正可归结为以下优化问题

s.t.VLB≤p≤VUB

(6)

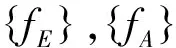
2 磨机传动系统扭转振动分析

某大型磨机的传动系统如图1所示。其中：1为电机；2为电机端高速联轴器；3为减速器端高速联轴器；4为减速器；5为减速器端低速联轴器；6为小齿轮轴联轴器；7为小齿轮；8为磨机(包括磨机筒体、大齿轮及载荷)。

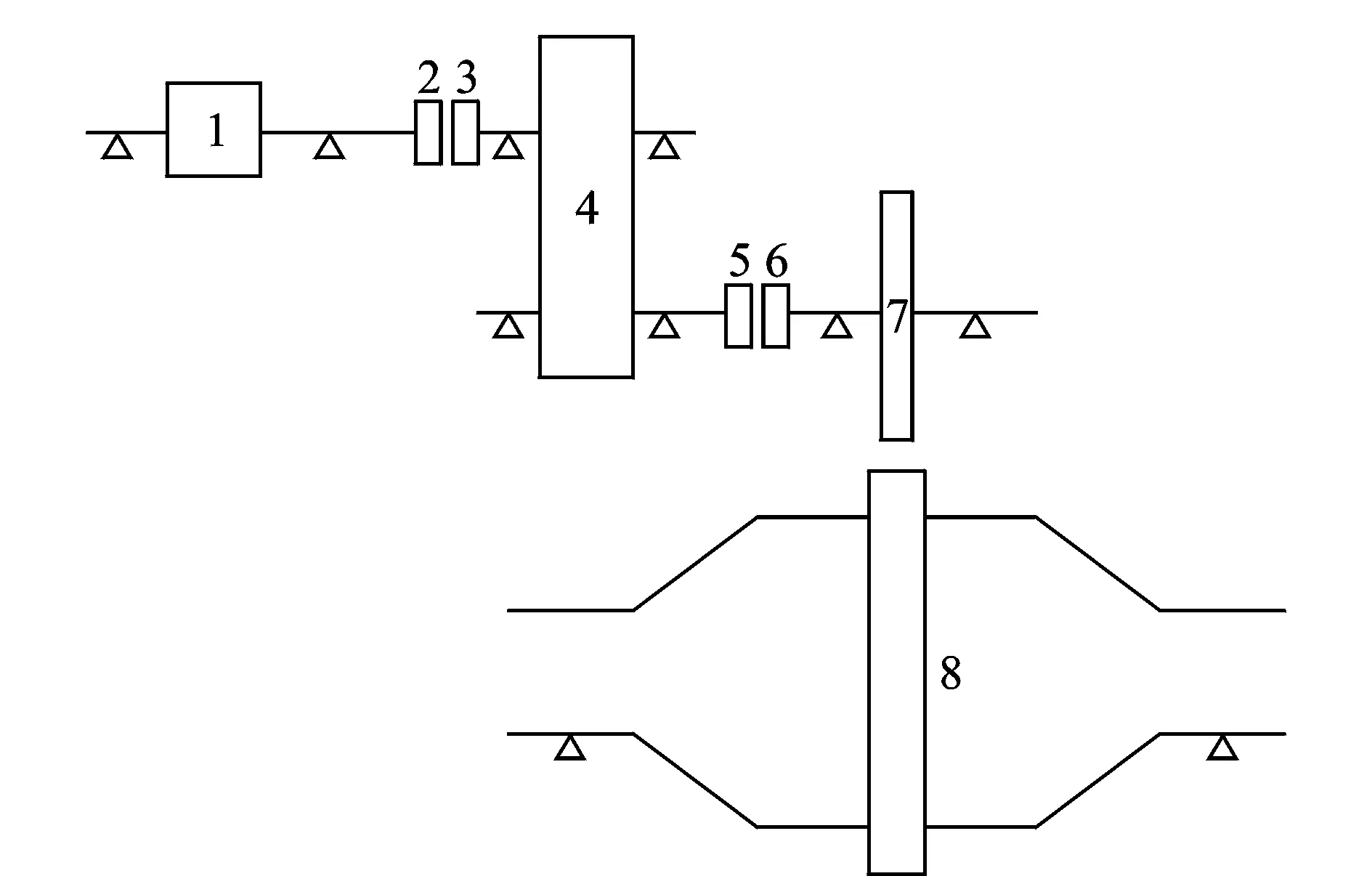
图1 某磨机传动系统简图Fig.1 The transmission system diagram of a mill

2.1 初始有限元模型的建立

当量扭转系统是研究传动系统扭振问题应用最为广泛的一种模型，它将系统中各部件作为集中质量考虑，通过扭转刚度连接，构成单一轴线的当量扭振模型[10]。建立当量模型时，原系统各部件参数可向任一传动轴等效转换，但需要按转换前后系统的动能和势能保持不变的原则，来确定转换后模型中各部件的参数。参数的等效方法依照式(7)和式(8)

(7)

(8)

其中：Ir，Kr分别为第r轴上的转动惯量和扭转刚度；Is，Ks分别为等效到第s轴上的转动惯量和扭转刚度；ur-s为第r轴和第s轴的转速比。

笔者使用有限元软件PATRAN建立传动系统的集中质量有限元模型，该模型共有8个转动惯量和7个扭转刚度，分别为依照式(7)、式(8)等效到高速电机轴后各个部件的转动惯量及其之间的扭转刚度，如图2所示。

图2 某磨机传动系统归一化扭振模型
Fig.2 The normalized torsional vibration model

2.2 模型的修正

对于待修正参数的选择，由于传动系统各部件在几何参数和材料确定后，所有的转动惯量J1～J8以及轴的扭转刚度K1，K3，K4，K6都可以确定，但是在传动系统复杂工况下，联轴器的扭转刚度K2，K5及齿轮啮合刚度K7具有存在误差或不确定性，所以被选作待修正参数，分别用A，B，C表示。利用正交设计方法，确定各组样本数据，基于方差分析得出了所有模态的显著性参数筛选结果，见表1(取显著水平α=0.05)。

表1 显著性参数筛选结果

Tab.1 The result of significant parameters selection

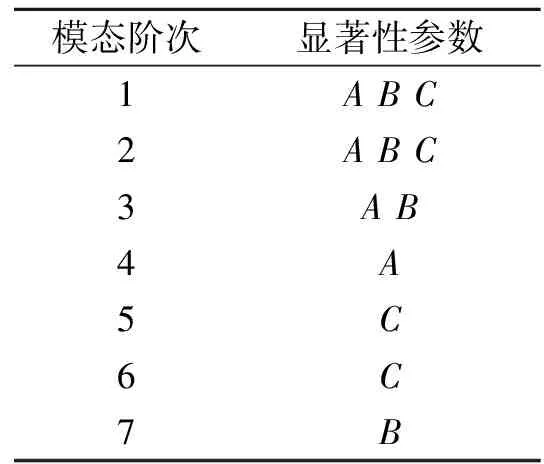
模态阶次显著性参数1ABC2ABC3AB4A5C6C7B

拟合含交互项的三次多项式响应函数，至少需要13组样本数据，但是由于之前正交设计确定的样本数据只有9组，于是笔者又采用均匀设计方法确定新的样本数据，最终拟合响应面的样本数据增至20组。以模态频率为因变量，以3个待修正参数为自变量，拟合含交互项的三次多项式响应函数。由于设计空间范围过小，会造成样本点代表性不足，影响响应面的精度，也会造成目标值不在响应面所表示的范围内，造成修正结果失效的问题。图3是第1阶模态频率的直观响应面曲面，[-1,1]是参数归一化空间，从图中可以看出在参数设计空间内，该阶模态频率的实测值6.26 Hz在响应面表示范围5.6～6.4 Hz内，表明参数的设计空间范围是合理的。

图3 第1阶模态频率的响应面Fig.3 The response surface of first order modal frequency

以磨机产生振动的实测模态频率作为目标值，基于响应面并通过Matlab对初始有限元模型进行修正。修正的结果见表2。从表2中可以看出，7阶模态频率的最大误差由-7.03%降为4.24%，均方误差由5.21%降为2.01%，说明有限元模型的精度有明显改善，更接近实际传动系统的情况。

表2 修正前后频率及误差

Tab.2 The frequencies and errors before and after the updating

模态阶次目标值/Hz初始值/Hz修正后值/Hz初始误差/%修正后误差/%16．265．826．15-7．03-1．76224．2925．9325．326．754．24370．3268．8371．86-2．122．194171．40163．42170．61-4．66-0．465216．29217．47214．860．55-0．666443．91419．27448．53-5．551．047562．74528．15566．82-6．140．73

2.3 模态频率的调整

判断系统是否共振的一种方法是基于坎贝尔图，观察系统工作频率是否落在了半功率共振区[11]。考虑到阻尼比为0.1时发生共振的半功率带宽约是±10%，所以由系统实际的固有频率及系统的工作频率得到传动系统的坎贝尔图如图4所示。传动系统小齿轮工作频率2.8及53.55 Hz的2倍频及3倍频与第1、第4阶模态有冲突(图中椭圆圈住部分)，此外第2、第7阶模态与磨机筒体工作频率9.52 Hz的3倍频以及减速器工作频率314 Hz的2倍频有冲突的危险，因此需要提高第1、第4阶模态频率，以避开系统工作频率，同时也要避免第2、第7阶模态频率与工作频率冲突的发生。

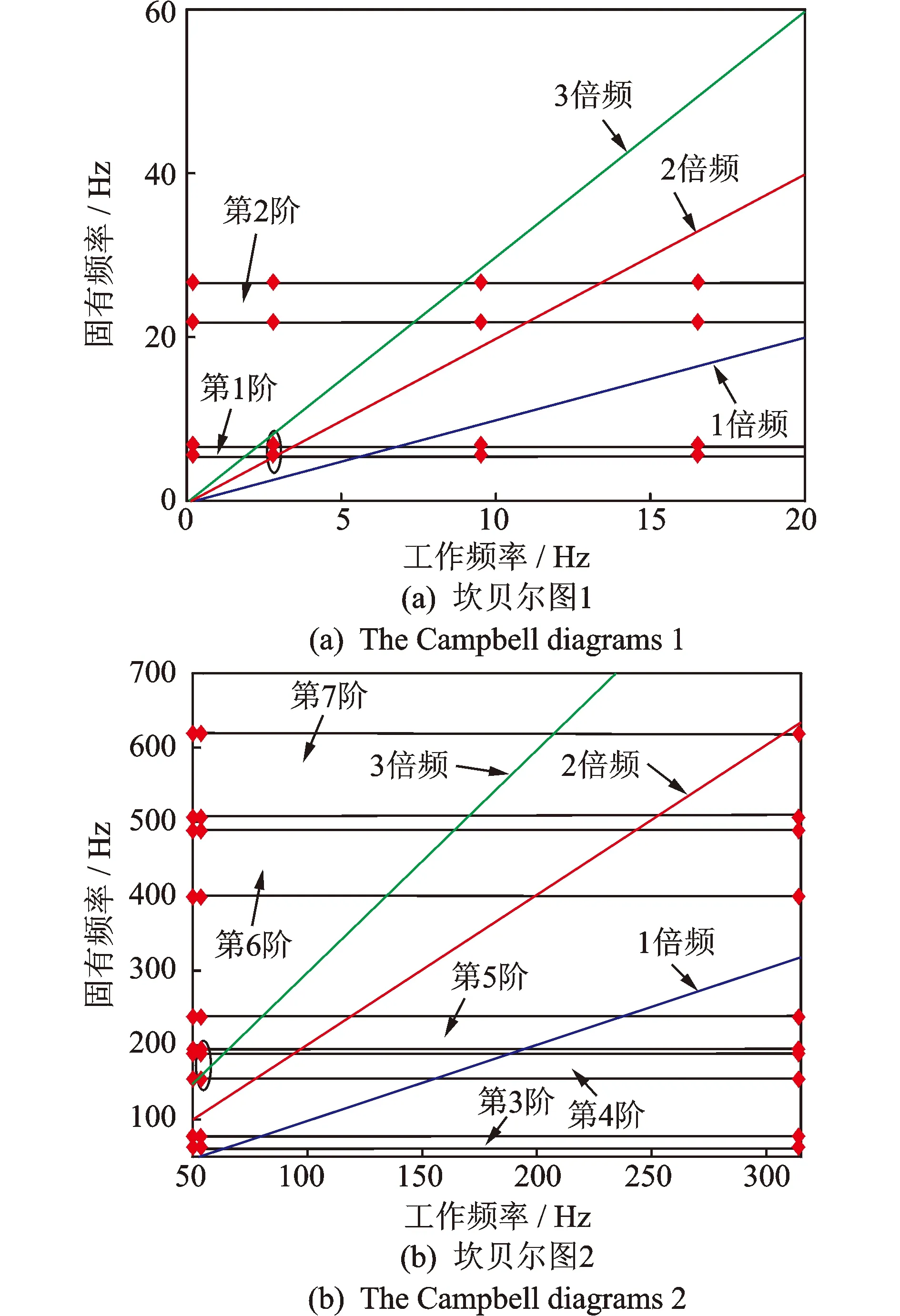
图4 传动系统的坎贝尔图Fig.4 The Campbell diagrams of transmission system

再次通过基于响应面的有限元修正方法，选择出对第1，2，4，7阶模态影响显著的可调参数J2，J3，K2，J5，J6及K5等，即联轴器的转动惯量与扭转刚度，在参数设计空间内确定样本数据，拟合响应面。以第1、第4阶频率提高后的4阶模态频率为目标值，以联轴器的转动惯量与扭转刚度为待修正参数，基于响应面并通过Matlab对新的有限元模型再次修正，得到修正过程中参数变化曲线如图5所示。

图5 参数变化曲线Fig.5 The changing curves of parameter

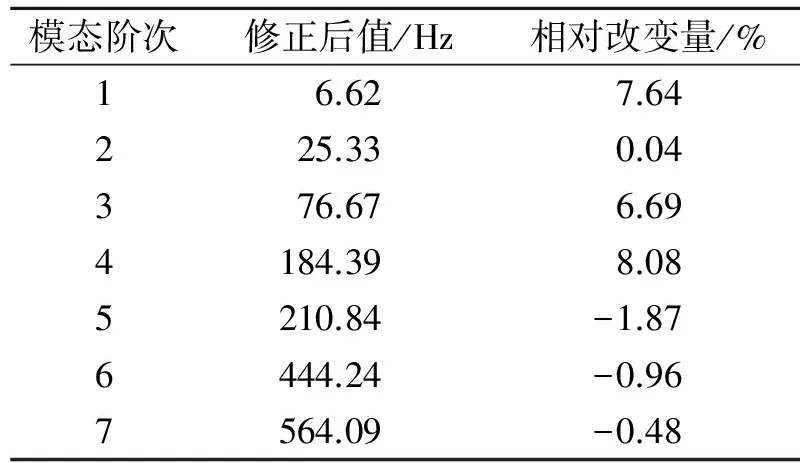
修正后的频率见表3。从表3可以看出，修正后的第1、第4阶模态频率得到提高，分别由6.15，170.61 Hz增至6.62和184.39 Hz。虽然其他模态也有变化，但都避开了系统的工作频率，远离半功率共振区。将修正后的联轴器各参数等效值按式(7)、式(8)换算为实际值，其结果及相对调整量见表4，根据优化设计后的联轴器各参数值调整磨机传动系统，结果表明磨机运行稳定，避免了共振现象的发生。

表3 修正后频率及相对改变量

Tab.3 The frequencies after updating and the values of relative change

模态阶次修正后值/Hz相对改变量/%16．627．64225．330．04376．676．694184．398．085210．84-1．876444．24-0．967564．09-0．48

表4 优化前后联轴器各参数值及调整量

Tab.4 The values of coupling parameters before and after optimization and adjustment

可调参数修正前修正后调整量/%转动惯量/(kg·m2)J237．236．5-1．88J366．864．3-3．74J598．7112．914．39J696．3111．315．58扭转刚度/((N·m)·rad-1)K21．31×1071．63×10724．43K55．63×1086．05×1087．46

3 结束语

响应面模型可以准确地反映设计参数与特征量之间的关系，有效替代有限元模型，避免每次迭代修正都要进行有限元分析，具有快速运行模型的特点。将响应面法应用到机械传动系统扭转振动的研究上，从不确定性因素中合理选取显著参数，以实测共振模态频率为依据，进行模型修正，进而对传动系统进行优化。实践表明，优化后的磨机运行稳定，性能良好，达到了工程要求。针对大型机械传动系统扭振问题，若在设计和研制阶段就利用上述方法对其进行分析，可以为设备良好的可靠性及动态性能提供保证。

[1] 朱坤泉，徐林发.建材机械工程手册[M].武汉:武汉工业大学出版社，2000:459-461.

[2] 黄之初，王高平，郭俊才.边缘传动球磨机系统的故障诊断及研究[J].武汉理工大学学报，2005，27(3):74-76.

Huang Zhichu，Wang Gaoping，Guo Juncai. Fault diagnosis and research on ball mill system of edge-transmission[J]. Journal of Wuhan University of Technology，2005,27(3):74-76. (in Chinese)

[3] Fei Qingguo，Li Aiqun，Miao Changqing. Dynamic finite element model updating using meta-model and genetic algorithm[J].Journal of Southeast University，2006，22(2):213-217.

[4] 任伟新，陈华斌.基于响应面的桥梁有限元模型修正[J].土木工程学报，2008,41(12):73-78.

Ren Weixin，Chen Huabin. Response-surface based on finite element model updating of bridge structures[J]. China Civil Engineering Journal，2008，41(12):73-78. (in Chinese)

[5] 费庆国，韩晓林，苏鹤玲.响应面有限元模型修正的实现与应用[J].振动、测试与诊断,2010,30(2):132-134.

Fei Qingguo，Han Xiaolin，Su Heling. The implementation and application of finite element model updating based on response surface[J]. Journal of Vibration，Measurement & Diagnosis，2010，30(2):132-134.(in Chinese)

[6] 常涛,郭勤涛,张保强.应用模型修正方法的印制电路板参数识别[J].振动、测试与诊断,2013,33(3):509-513.

Chang Tao，Guo Qintao，Zhang Baoqiang. Identification of physical parameters of printed circuit board based on model updating method [J]. Journal of Vibration，Measurement & Diagnosis，2013，33(3):509-513. (in Chinese)

[7] 程霄翔，费庆国，何顶顶，等. 基于响应面的大型输电塔结构有限元模型动力修正[J].振动与冲击，2011，30(5):116-122.

Cheng Xiaoxiang，Fei Qingguo，He Dingding，et al. Dynamic updating of a large transmission tower′s finite element model based on response surface methodology[J]. Journal of Vibration and Shock，2011，30(5):116-122. (in Chinese)

[8] 费庆国，张令弥，李爱群，等.基于统计分析技术的有限元模型修正研究[J].振动与冲击，2005,24(3):23-26.

Fei Qingguo，Zhang Lingmi，Li Aiqun，et al. The finite element model updating based on statistical analysis techniques[J]. Journal of Vibration and Shock，2005，24(3):23-26. (in Chinese)

[9] 郭勤涛，张令弥，费庆国.用于确定性计算仿真的响应面法及其试验设计研究[J].航空学报，2006,27(1):55-61.

Guo Qintao，Zhang Lingmi，Fei Qingguo. Response surface method and its experimental design for deterministic computer simulation[J]. Journal of Aeronautics，2006，27(1):55-61. (in Chinese)

[10]徐燕申.机械动态设计[M].北京:机械工业出版社，1992:98-103.

[11]张保强，陈国平，郭勤涛.机械传动系统扭转振动的模型修改不确定性分析[C]∥第十届全国振动理论及应用学术会议论文集.南京：中国振动工程学会，2011：821-828.