考虑轮径影响的履带式车辆振动分析*

2017-01-09孙中兴唐力伟歹英杰

振动、测试与诊断 2016年6期

关键词：波谷平度履带

孙中兴, 唐力伟, 汪伟, 歹英杰

(军械工程学院火炮工程系石家庄，050003)

考虑轮径影响的履带式车辆振动分析*

孙中兴, 唐力伟, 汪伟, 歹英杰

(军械工程学院火炮工程系石家庄，050003)

在车辆垂向振动的研究中往往把路面不平度直接作为路面对车辆的位移激励，未考虑车轮与路面间的几何关系对位移激励的影响。针对这种情况,分析了履带式车辆负重轮的轮径对车辆垂向振动的影响机理，推导了考虑履带滤波效应和负重轮轮径的车辆等效路面位移激励的计算方法，建立了描述车辆竖向振动的状态方程及其仿真模型，并针对正弦路面波形、周期性矩阵脉冲波形、单位冲击波形以及实际路面波形下车辆的振动进行了仿真分析。结果表明，路面位移激励只有考虑轮径的影响才能反映出车辆冲击、振荡、“平滑”等在行驶过程中与路面的真实相互作用情况。试验结果证明了所述等效路面位移激励算法和正弦路面下车辆的振动特性的正确性。

履带式车辆；路面不平度；轮径；等效位移激励；状态方程

引言

车辆与道路的相互作用问题是近年来一个新的研究领域[1]。车辆在路面不平度的影响下产生振动，这种振动又反过来作用于道路结构，车辆与路面之间的相互作用机理是这项研究的前提和关键。道路对车辆的影响是通过路面不平度造成对车辆的垂向激励的方式实现的[2-5]。传统的研究方法忽略了车轮与路面之间的几何关系以及相对位置对路面产生的位移激励的影响，直接把路面不平度等效为车辆所受的位移激励[6-8]，势必会造成很大的分析误差。

为了提高研究的精确度和真实性，笔者在分析履带式车辆负重轮的轮径对车辆垂向振动影响机理的基础上，推导了考虑履带滤波效应和负重轮轮径的车辆等效路面位移激励的计算方法，建立了履带式车辆的动力学模型，对正弦路面波形、周期性矩阵脉冲波形、单位冲击波形以及实际复杂路面波形下车辆的振动进行了仿真，探究了负重轮直径对车辆和路面之间相互作用的影响，并通过试验证明了方法的正确性。

1 考虑履带和轮径影响的路面激励计算

1.1 轮径对车辆输入激励的影响分析

轮径对车辆路面激励的影响主要是由行驶过程中车轮与地面之间存在的进入角和离去角所造成的。由图1可以看出,进入角和离去角的存在使车轮与地面的接触位置不一定是在车轮的最低点，这就导致路面的空间域模型与路面对车辆的空间位移激励之间存在随进入角或离去角而变化的相位差。若进入角和离去角同时存在时(见图2)，车轮与地面两接触点之间的路面波形便被车轮“滤掉”，无法对车辆产生激励作用。因此，传统的以地面波形作为车辆空间激励的做法势必会造成很大的误差。

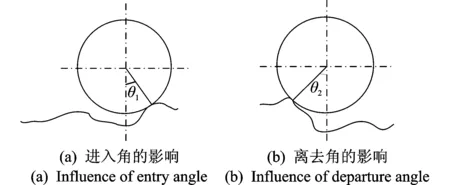
图1 轮径对车辆所受位移激励影响示意图Fig.1 The influence of the wheel′s diameter

1.2 考虑履带和轮径影响的路面位移激励计算

1.2.1 履带对路面位移激励的影响

路面上铺设履带，对路面不平度低频成分影响较小，对高频成分，特别是上限频率有较大影响[8]:a.滤掉了路面不平度中比履带节空间频率更高的成分，使履带节的空间频率成为履带车辆路面不平度的上限频率，；b.两块履带板连接处的不平，又在路面不平度中添加了与履带节相应的周期性激励。由文献[8]可知，车辆正常行驶时履带板连接处的激励频率远低于车体垂直振动固有频率，其影响甚微。

履带不直接与车身相连，故地面对履带(不与负重轮接触的履带部分)的作用力通过履带的拉伸力传递给负重轮，再由负重轮传递给车身，即车身的重量都只作用在负重轮(包含与负重轮接触的履带部分)上，地面对履带的垂直作用力只被用来平衡履带的拉力。一方面悬架系统的存在缓解履带拉力的增加，使其稳定在较小数值；另一方面在结构路面上路面不平度的幅值相对较小，履带近乎水平，其拉力的垂直分量可忽略不计[9]，且履带的存在不会对负重轮与地面的接触产生明显影响。

1.2.2 考虑进入角和离去角影响的路面位移激励计算

不考虑负重轮表层胎胶和地面弹性的影响，假设负重轮与地面之间的作用是完全刚性的。取步长为Δt，在ti时刻(此时负重轮最下端的坐标为xi，负重轮实际所受的激励位移为h(xi)(并不等同于路面不同度曲线在xi处的取值)，在[xi-R,xi+R]区间内定义

(1)

其中：u(x)为路面不平度曲线在x处的取值；R为车轮的半径；θ1(2)为车轮的进入角或离去角；Δx为x与xi的差值。

取步长Δx，在区间[xi-R,xi+R]内依次求取Δh=H(xi+1)-h(xi)，并通过Δh的符号来判断进入角对位移激励造成的影响，具体如下

(2)

用同样的方法可求得ti+Δt时刻路面对车辆的位移激励，依次递推可得到任意时刻的位移激励。

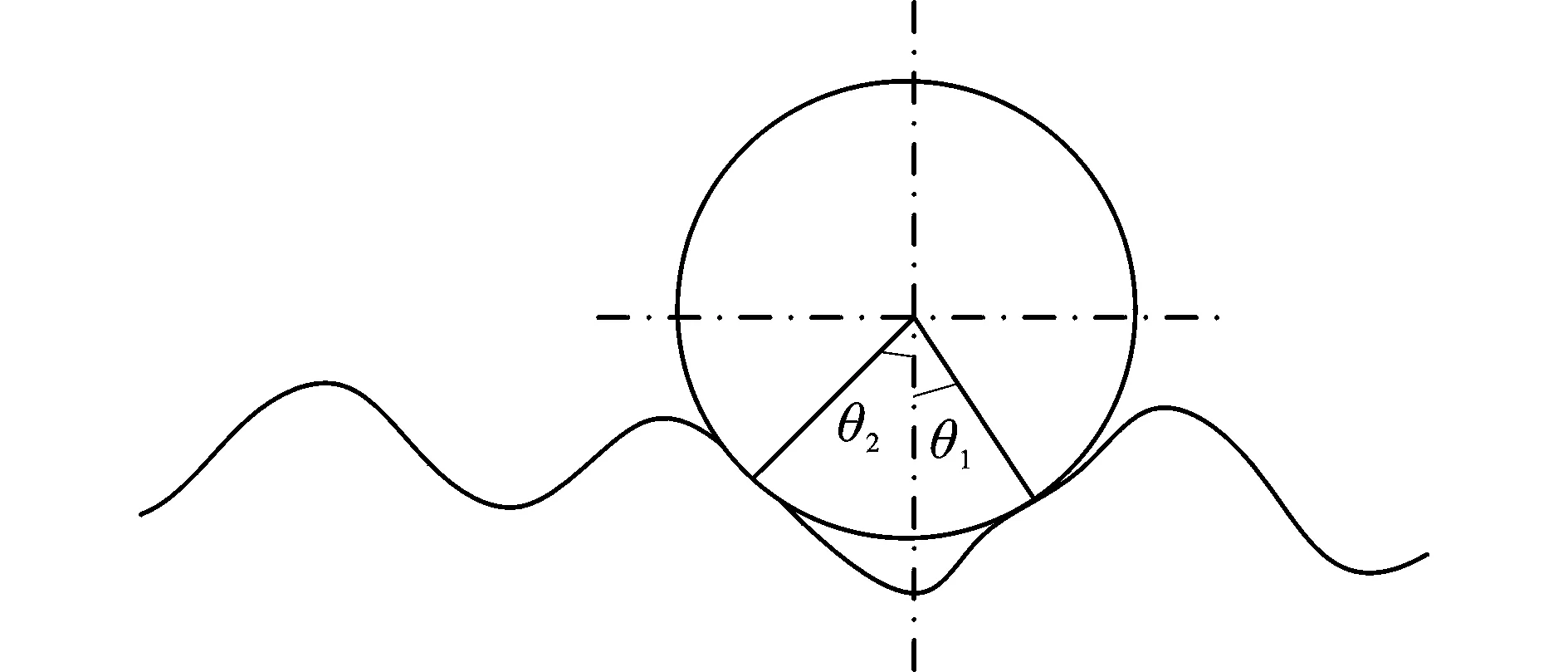
图2 轮子地面相互作用示意图Fig.2 Interaction between wheel and road

2 履带式车辆垂向振动分析

2.1 车辆动力学模型的建立和求解

笔者所研究的履带式车辆每侧有1个主动轮、1个诱导轮和6个负重轮，忽略主动轮和诱导轮对车辆垂向振动的影响，履带对车辆随机振动的影响通过对路面不平度功率谱做预处理来实现。由于两侧履带通过车辙多数情况下较接近，且车辆侧摆时车轮与履带之间会有摩擦阻尼的作用令侧摆迅速消失，故忽略侧摆的影响[10]，建立如图3所示的车辆1/2模型。

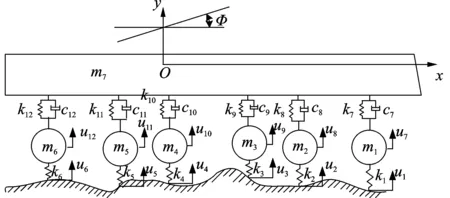
图3 某履带式自行火炮垂向振动模型Fig.3 Vibration model of self-propelled artillery

模型的车身质量为m7，转动惯量为I，负重轮的质量为m1～m6，在x轴上的坐标为l1～l6。各负重轮胶胎通过履带与地面相互作用的等效刚度为k1～k6，悬架的等效刚度系数和等效阻尼系数分别为k7～k12和c7～c12。u1～u6,z1～z6，Y分别为路面对各负重轮的激励、负重轮和车体在垂直方向上的位移，车体的纵向摇摆角为Φ。由Lagrange公式可得车身的动力学方程为

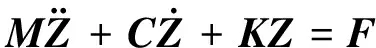
(3)

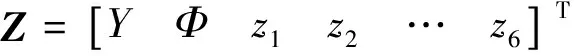
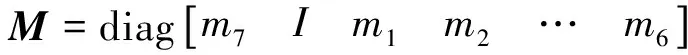
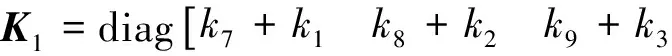
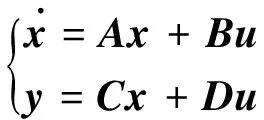
(4)

其中

每个负重轮之间的激励具有相同的形式，仅存在时间的滞后，且其滞后量可由轴距和行驶组度计算出来。得到状态方程的仿真模型如图4所示。

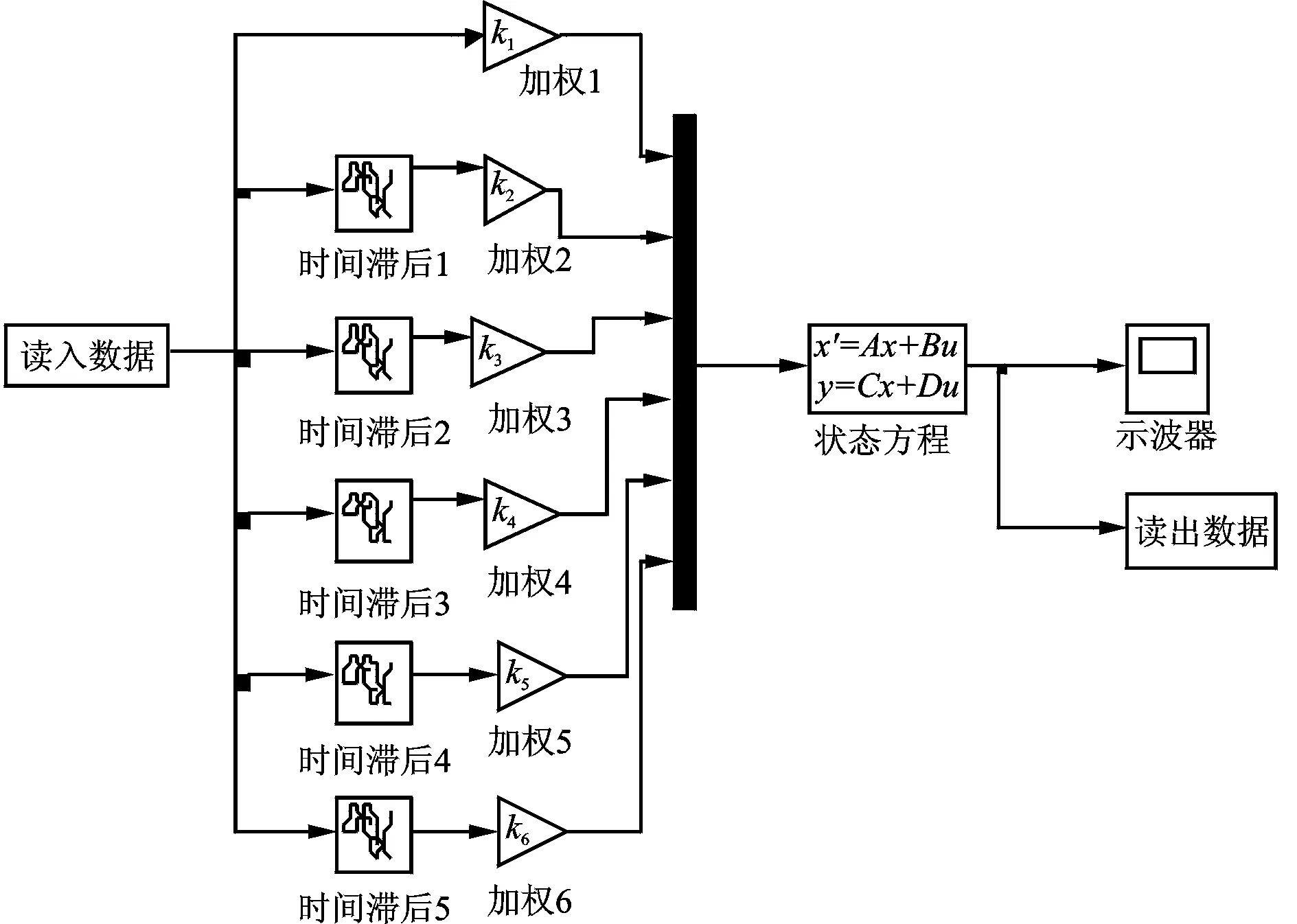
图4 车辆动力学状态方程的仿真模型Fig.4 Simulation model of tracked vehicle

2.2 考虑轮径影响的车辆垂向振动特性分析

2.2.1 正弦路面波形下轮径对振动的影响

本研究中履带式车辆的各项参数如下：m7=9 682.8 kg；I=12 760.87 (kg·m)；R=0.28 m2；m1-6=62.5 kg；k1-6=164 250 N/m;k7-12=29 024.16 N/m;c7-12=2 183.94(N·s)/m。令路面的空间波形函数为

y=-0.015sin(3.3aπx)

(5)

图5蓝色实线所示为车辆行驶速度v=2.5km/h，a取不同值时负重轮1所受的实际路面激励位移u1的时间波形曲线，虚线为路面的时间波形图。可以看出，由于负重轮直径的影响，车辆所受的实际激励位移与路面实际波形存在差异，且频率越高差距越明显，具体体现在波形在波峰附近变得更加平缓，在波谷位置变得更加急促。当路面波形的周期减小到一定程度时负重轮无法与波谷底部接触，激励位移在波谷位置出现突变，如图5(c)所示。

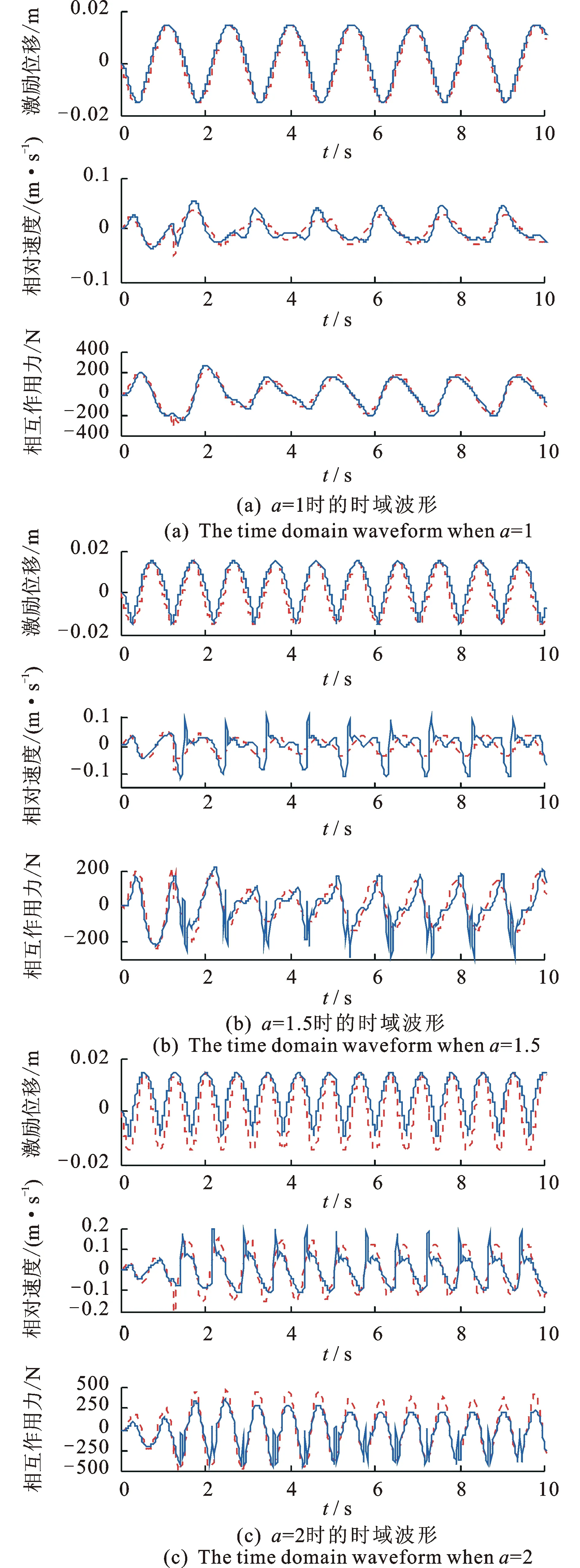
图5 车辆在正弦路面行驶时的时域波形Fig.5 Curve when vehicle moving on a sine road

以第二负重轮和车身之间的相对速度y以及负重轮2与地面之间的作用力f为例来分析轮径对车身振动产生的影响，其振动波形如图5所示。由图5可以看出，不考虑轮径的影响时车辆的稳态响应是一种正弦波形，但轮径的影响使实际波形与正弦波形有明显差别，具体反映如下：当路面波形的频率较小时(a=1)，轮径的影响并不十分明显；随着频率的增大(a=1.5)，波谷位置的激励位移出现“突变”，产生对车辆的冲击力，造成负重轮与车身之间的悬架系统急剧压缩，y迅速减小，当车辆驶离波谷位置时被压缩的悬架反弹形成振荡，效果类似于瞬间碰撞；频率继续增大使负重轮无法与波谷接触时(a=2)，车辆在波谷位置受到的激励远小于路面波谷的位置坐标，故y变化的幅值比不考虑轮径影响时小，波谷处依然有冲击力的存在，驶离波谷后的振荡效应依然明显。

2.2.2 其他路面波形下轮径对振动的影响

采用1.2节所述的处理方法可对任意路面波形进行考虑车辆轮径影响的预处理，图6和图7为周期性方波和冲击波形的处理结果。

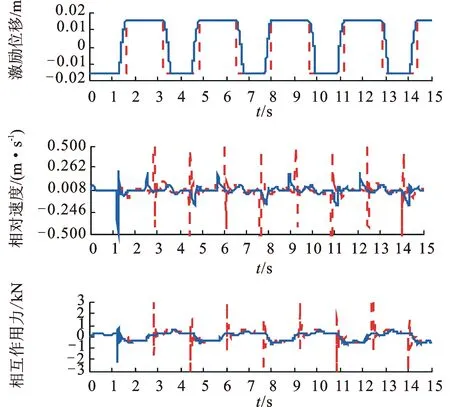
图6 车辆在矩形脉冲路面行驶时的时域波形Fig.6 Curve when vehicle moving on a rectangular road

图6中虚线表示不考虑轮径影响时的曲线，实线表示考虑轮径影响时的曲线。由图6可以看出,考虑轮径将影响时车辆所受的位移激励变得更加平滑，车辆振动相对较弱，负重轮进入和离去矩形脉冲的瞬间冲击效应明显减弱。

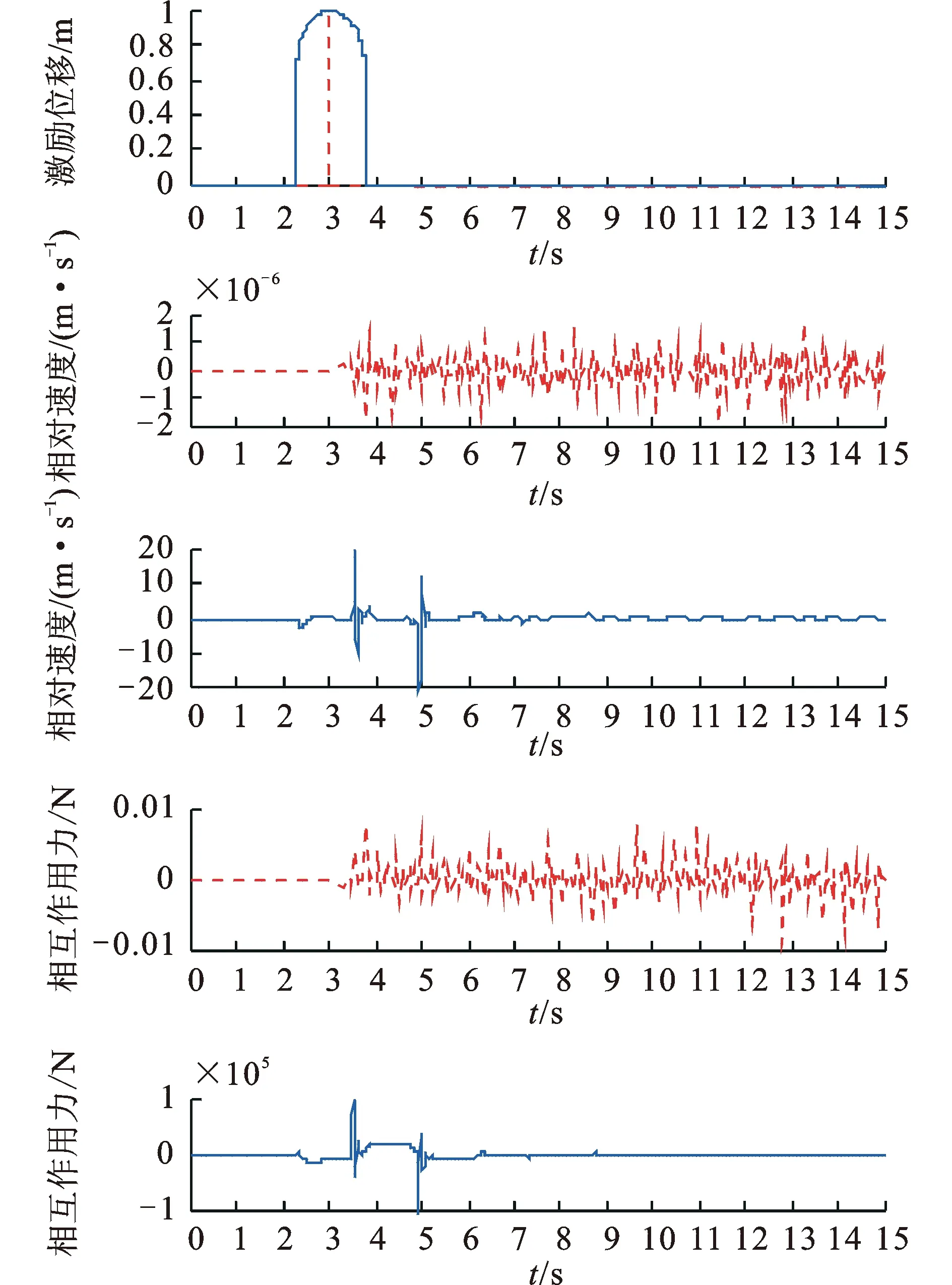
图7 车辆在冲击路面行驶时的时域波形Fig.7 Curve when vehicle moving on a shock road

图7中虚线表示不考虑轮径影响时的曲线，实线表示考虑轮径影响时的曲线。轮径的存在使原有的冲击信号变为“拱形门”信号，负重轮与地面之间的冲击效应由1次变为2次，且强度大大增加。

3 复杂路面环境下轮径的影响

第2节中对正弦、方波及冲击波等波形的路面进行了分析，而实际路面要比这些理想路面复杂。对于特定路面其路面不平度可由实测得到，但无法保证其是否具有代表性。解决该问题的方法是在已知的路面自功率函数Gq(n0)的基础上建立路面空间模型，比较常用的方法是谐波叠加法[11-12]，其路面不平度模型为

(6)

其中：l为路面的走向长度；Δn为频率区间；θi为[0.2 π]均匀分布、相互独立的随机变量。

转换为时域模型为

(7)

其中：t=l/v；fmid-i=nmid-iv为nmid-i所对应的时间频率。

以H级路面为例，由式(7)可得其路面不平度模型如图8第1图的红色虚线所示，运用本方法求得的位移激励如图7第1图蓝色实线所示。将二者带入图4所示的仿真模型中得图8所示的相对速度和相互作用力曲线。为增加可视性，图8只给出了前5s的波形。由图8可以看出，实际位移激励与路面不平度的走向基本一致，但路面不平度中跨度较小波谷在实际位移激励中被“滤掉”，或被“削尖”。考虑轮径影响时车辆振动相对较弱，负重轮与地面之间的作用力变化也相对平缓，但“波谷削尖”处的作用力会有明显的冲击现象。

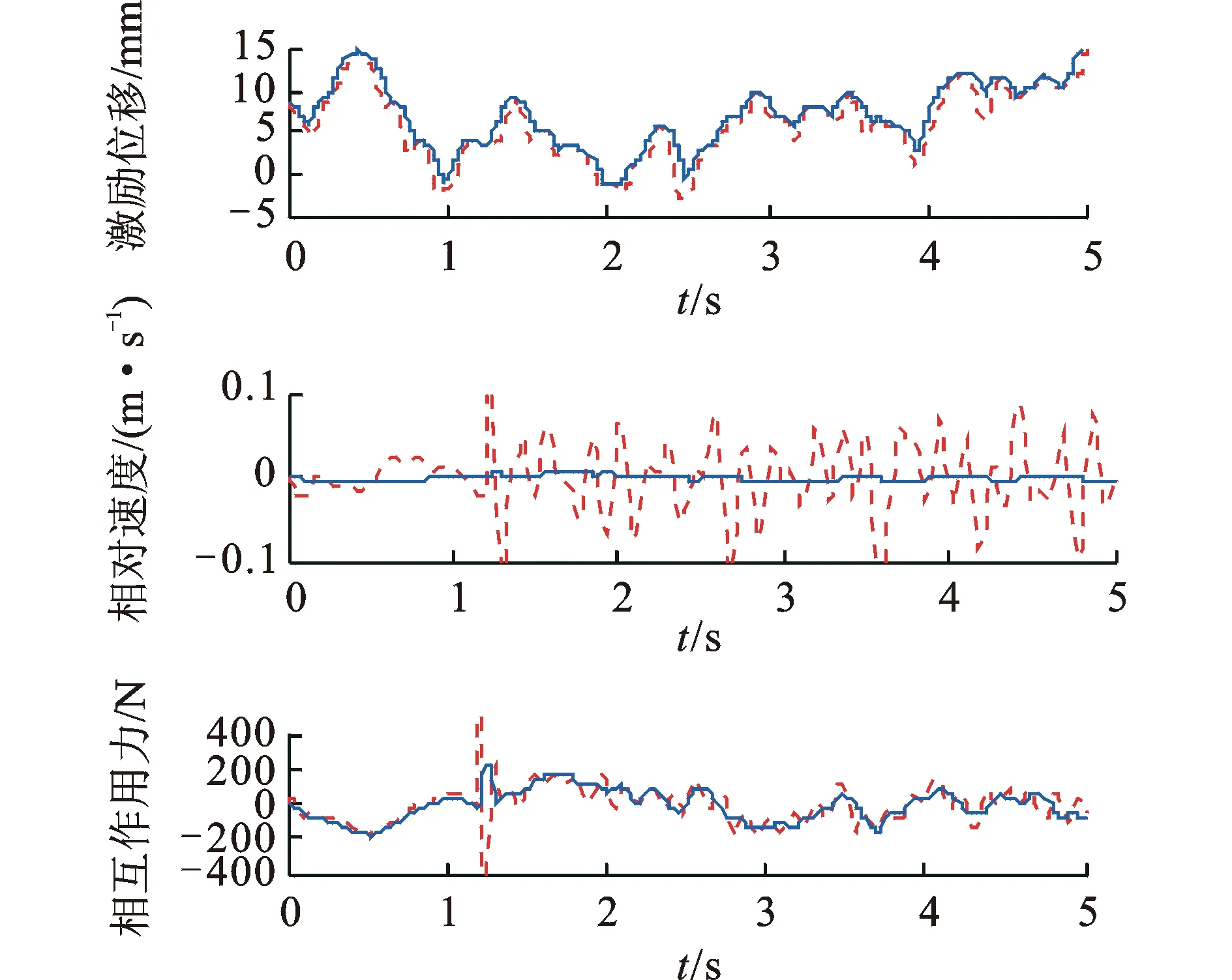
图8 车辆在仿真路面行驶时的时域波形Fig.8 Curve when vehicle moving on a simulink road

为进一步研究负重轮直径对路面谱的影响，笔者做出了路面不平度和位移激励在对数坐标系下的功率谱图，见图9。由图9可以看出：路面不平度功率谱密度大致呈一条倾斜的直线；位移激励在低频区域与路面不平度功率谱基本重合，从大约1/m开始位移激励功率谱密度下降趋势明显放缓，走势基本呈水平，这是由于处于该频率段的波谷被“消尖”的缘故；约10/m后位移激励的功率谱密度急速下降,与路面不平度的功率谱密度形成剪刀差，这是由于随着频率的增加,越来越多的波谷被负重轮“滤掉”，路面不平度中的高频成分大部分都未形成垂向激励。

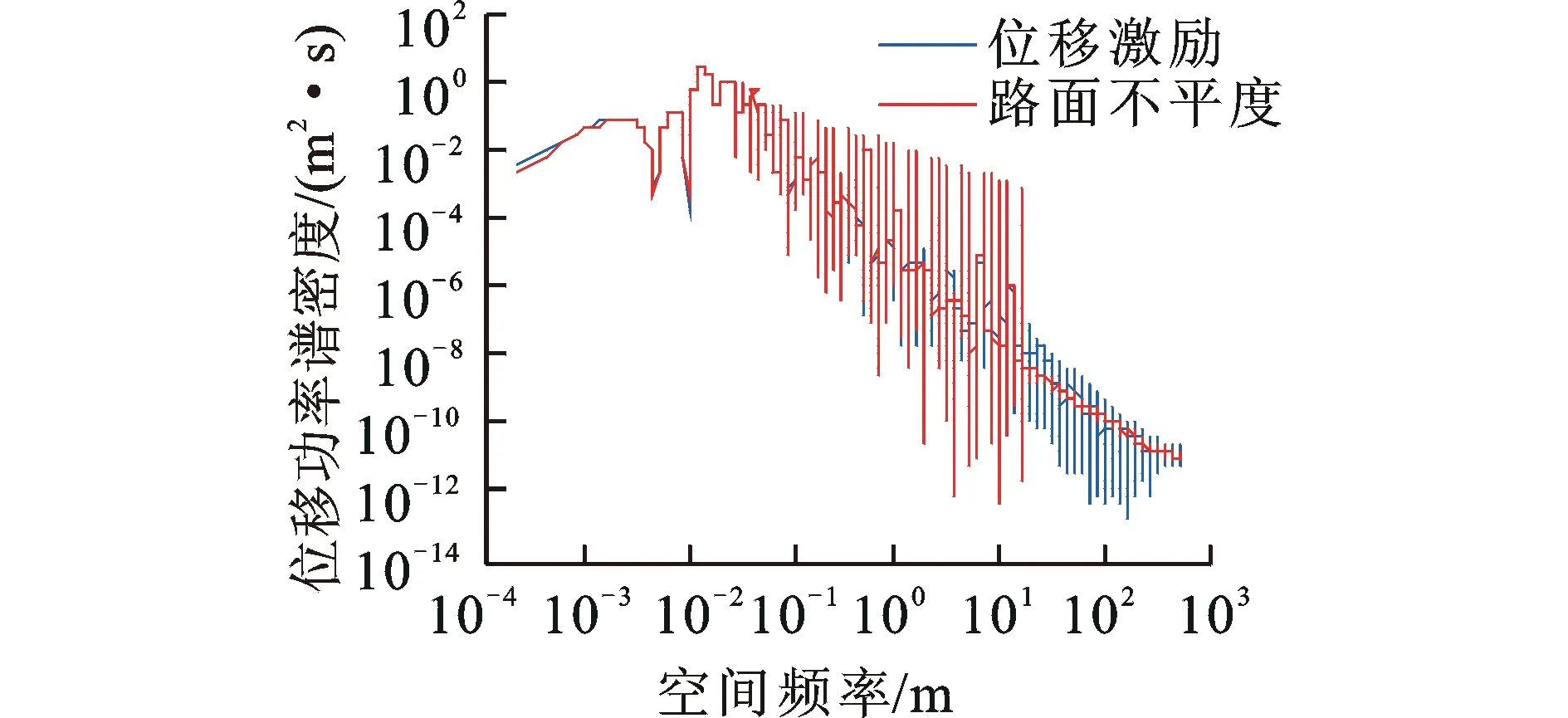
图9 功率谱估计Fig.9 Power spectrum estimation

大部分履带式车辆都是功能性车辆，具有复杂的工作单元，各工作构件的频率成分差别大，故不能像简单的轮式车辆那样保证时间频率涵盖悬架频率而略去更高频的激励。

4 试验验证

为验证所提方法的合理性，在某试验中心的正弦试验路面上利用牵引装置使所研究履带式车辆以2.5km/h的速度稳态行驶，在第二负重轮的轴头位置和与其保持垂直的车体部位之间安装拉线位移传感器来测量二者的相对位移，具体安装位置如图10所示。其中，试验路面宽度为4m,路面基本波形为正弦形，纵向坡度不大于5‰，波形函数为u=15sin(4.8x)(mm),路面形状如图11所示。

图10 位移传感器安装图Fig.10 The sensor disposition at the vecicle

图11 试验路面波形示意图Fig.11 Curve of the experience road

对所测得的相对位移进行差分运算便可得到负重轮与车体之间的相对速度曲线，结果如图12中的蓝色实线所示。从图12可以看出，试验曲线与相同条件下的仿真曲线波形和变化趋势都基本吻合。车辆行驶至波谷位置时负重轮与车身之间的相对速度迅速减小，驶离波谷位置后具有明显振荡，这些现象都与2.2节的分析吻合良好，验证了考虑轮径的路面位移激励算法的正确性。

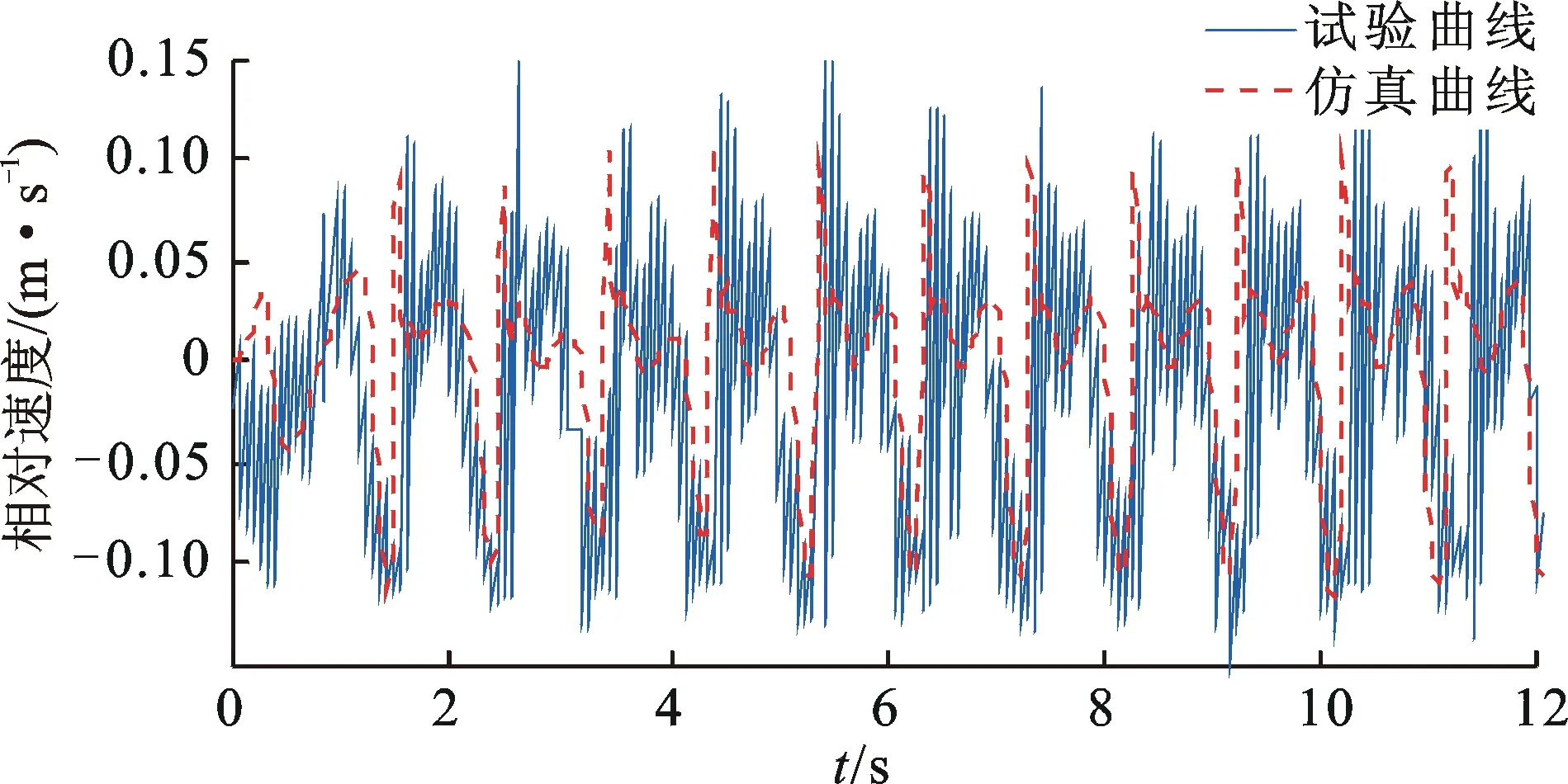
图12 负重轮与车体相对速度的试验值Fig.12 Curve of the experience

5 结论

1) 分析了履带式车辆负重轮的轮径对车辆垂向振动的影响机理，推导了考虑履带滤波效应和负重轮轮径的车辆等效路面位移激励的计算方法。

2) 针对正弦路面波形、周期性矩阵脉冲波形和单位冲击波形下车辆的振动进行了仿真分析。结果表明路面位移激励只有考虑轮径的影响才能反映出车辆冲击、振荡、“平滑”等在行驶过程中与路面的真实相互作用情况，提高了模型的精确度和真实性。

3) 采用谐波叠加法构件了真实路面的空间和时间模型，分析了实际路面环境下负重轮轮径对车辆垂向振动以及路面功率谱的影响。

4) 设计试验对本研究理论进行了验证。

5) 所提出的等效路面位移激励的计算方法适用于任意波形的路面。

[1] 许海亮，袁勇，屈铁军，等. 考虑路面不平度因素的车路耦合振动模型的建立[J]. 振动与冲击，2014,33(19)：152-156.

Xu Hailiang, Yuan Yong, Qu Tiejun，et al. Dynamic model for a vehicle-pavement coupled system considering pavement roughness[J]. Juornal of Vibration and Shock, 2014,33(19)：152-156.(in Chinese)

[2] Cebon D. The dynamic unteraction between wheeled vehicles and road surface[D]. London：Cambridge University,1985.

[3] Mikhail M Y. Tree dimensional mechanistic analysis of vehicle-pavement interaction[D]. Phoenix：Arizona State University,1996.

[4] 刘大维，李国政，陈焕明，等.车辆随机动载作用下路面动态响应研究[J]. 农业机械学报，2011，42(2):28-33.

Liu Dawei， Li Guozheng， Chen Huanming，et al. Dynamic response of pavement based on random dynamic load of vehicle[J]. Transactions of the Chinese Society for Agricultural Machinery,2011，42(2)：28-33.(in Chinese)

[5] 王博，孙仁云. 考虑路面不平度的路面识别方法[J]. 机械工程学报，2012,12(24)：127-133.

Wang Bo, Sun Renyun. Road surface condition identifucation approach with consideration of road roughness[J]. Journal of Mechanical Engineering, 2012,12(24)：127-133.(in Chinese)

[6] 王良曦，王红岩. 车辆动力学[M]. 北京：国防工业出版社，2004：36-42.

[7] Kiureghian A D, Neuenhofer A. Pesponse spectrum method for multi-support seismic excitations[J]. Earth-quake Engineering and Structural Dynamics， 1992,21:713-740.

[8] 丁法乾. 履带式装甲车辆悬挂系统动力学[M]. 北京：国防工业出版社，2004：218-236.

[9] 刘辉，符升平，项昌乐. 不平整路面履带车辆动力传动系统扭转随机激励研究[J]. 农业机械学报，2010,41(12):1-6.

Liu Hui， Fu Shengping， Xiang Changle. Torsional random excitation of tracked vehicle powertrain system caused by road roughness[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010,41(12):1-6.(in Chinese)

[10]李志强. 基于逆动力学分析的履带车辆行驶路面识别研究[D].石家庄：军械工程学院，2010.

[11]常志权，罗虹，褚志刚. 谐波叠加路面输入模型的建立及数字模拟[J]. 重庆大学学报：自然科学版,2004,27(12):5-8.

Chang Zhiquan, Luo Hong, Chu Zhigang. Building model of road roughness[J].Journal of Chongqing University：Natural Science,2004,27(12):5-8.(in Chinese)

[12]王亚，陈思忠，郑凯锋. 时空相关路面不平度时域模型仿真研究[J]. 振动与冲击，2013,5(32)：70-74.

Wang Ya, Chen Sizhong, Zheng Kaifeng. Simulation research on time domain model of road roughness with time-space correlation[J]. Journal of Vibration and Shock, 2013,5(32)：70-74.(in Chinese)