基于高频数据的大维金融协方差阵的估计与应用

刘丽萍

（贵州财经大学数学与统计学院，贵阳550025）

0　引言

金融领域中，资产组合的构建依赖于不同资产间的协方差阵，协方差阵的估计效果直接影响到资产的权重，一般而言，协方差阵的估计效果越好，构建的投资组合越合理。但是，当今社会是信息爆炸的时代，随着数据可获得性的提高，很多金融机构便面临的是大规模高维度的金融资产，鉴于维数诅咒以及市场噪声的影响，如何估计大维资产的协方差阵是统计领域中一大难题。近年来，就大维协方差阵的估计问题已经引起了一些学者的关注，取得了许多研究成果，有关大维协方差阵估计方法是基于低频数据的，但是基于低频数据估计的协方差阵并不理想，这是因为低频数据损失了很多有用的信息。伴随着数据可获得性的提高，对于高频数据的研究引起了越来越多的学者的关注[1-4]，为了提高大维协方差阵的估计效率，Fan和Furger等（2015）[5]将因子分析和门限方法应用到大维金融高频协方差阵的估计中，解决了维数诅咒问题。本文在前人研究的基础之上，采用高频数据来估计大维金融资产的协方差阵，本文将主成分分析法和门限方法相结合应用到协方差阵的估计中，提出了新的协方差阵。的估计并不复杂，首先对基于高频数据的样本协方差阵进行谱分解，提取少数几个最优主成分来刻画协方差阵的主要信息；然后将门限函数应用到残差矩阵中，得到了对角分块残差矩阵，这不同于传统的基于软门限函数或硬门限函数得到的对角矩阵，它考虑到同一行业的资产之间的相关性较强，而将同一行业不同资产间的协方差元素替换为0并不合理，客观而言，对角分块残差协方差阵更为合理。

1　协方差阵的估计

1．1　新的协方差阵估计方法的提出

令X为观测到的p维资产的收益率向量，Δn为抽样频率，n为样本量，t为所取样本的时间跨度，则n=t/[Δn]，对于任意的1≤i≤n：

其对应的样本协方差阵的估计量为：

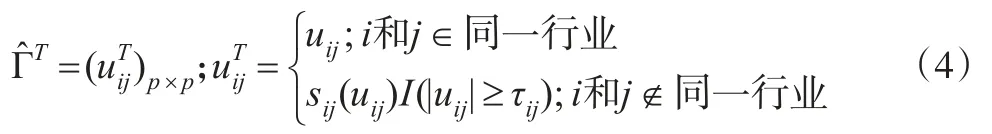
式（4）中，τij（τij＞0）代表的是门限函数，sij(⋅)代表的是广义收缩函数[6]。需要注意的是由式（4）得到的残差协方差矩阵是对角分块矩阵，这不同于传统的基于软门限函数或硬门限函数得到的对角矩阵，它考虑到同一行业的资产之间的相关性较强，而将同一行业不同资产间的协方差元素替换为0并不合理，客观而言，对角分块矩阵更为合理。

1．2　最优主成分数目的选择

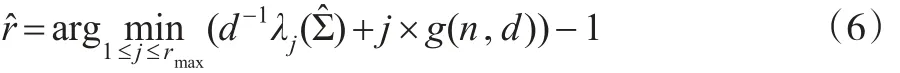
其中，rmax是最优主成分数目的上限，g(n,d)是惩罚函数，其表达式如下：

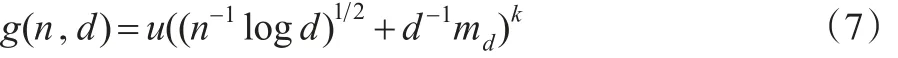
式（7）中u和k都是常数，md表示的是中非零元素的数目，根据A-Sahalia和Xiu等的研究知：最优主成分的数目=3，当的取值大于3时，协方差阵的估计结果并未有所改良。刘丽萍，马丹等（2015）[8]的研究指出：将主成分分析法应用在高维资产的协方差阵估计中时，随着资产维度的增加，最优主成分的数目趋于稳定，当主成分的数目为3时，其对应的损失函数较小，协方差阵的估计效果较好，从而进一步验证了AÏt-Sahalia和Xiu等的研究。所以在后文的研究中，选择的最优主成分的数目为3。

1．3　门限函数的选择

式（8）中C＞0，为常数，这里取C=0.5[10]。符号w表示的是收敛速率，对于p×p门限函数应用到，剔除噪声的影响后得到：

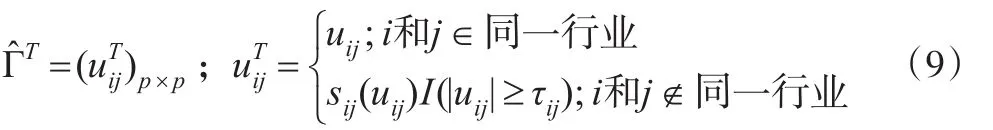
其中，I为示性函数，当|uij|≥τij时，I(⋅)=1，否则I(⋅)=0，|sij(uij)-uij|≤τij。本文选取的收缩函数的表达式为：

即当|uij|≥τij时，u=Sgn(uij)(|uij-τij|)，否则u=0。其中Sgn是符号函数，uij＞0时，Sgn(uij)=1；uij=0时，Sgn(uij)=0；uij＜0时，Sgn(uij)=-1。

2　模拟研究

2．1　数据的产生

本文根据AÏt-Sahalia和Xiu等的研究来产生高频数据，数据的产生步骤如下：

（1）建立d维资产的连续时间因子模型，模型的形式为：

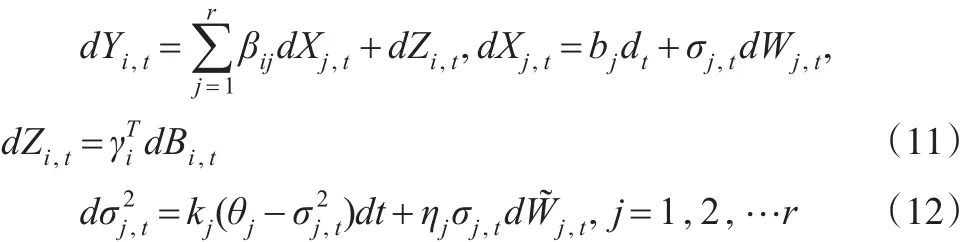
式（11）中，Wj(j=1,2,…r)是标准的布朗运动，(i=1,2,…,d)是d维的布朗运动，它们是相互独立的，Xj是第j个不可观测的因子，Z的协方差阵是对角分块矩阵，将对角分块矩阵定义为Γ，则Γ=γl。由式（12）知σj,t是时变的，其中j是标准的布朗运动，Ε(dWj,tj,t)=ρjdt。

（2）假定d维资产受到市场微观结构噪声εi,t(i=1,2,…,d)的影响，εi,t服从标准的正态分布，即εi,t～N(0,0.0012)，将εi,t加入到资产的对数价格Yi,t中，从而得到了受到市场微观结构噪声影响的对数价格。

（3）设定模型的参数，k=(3,4,5),θ=(0.09,0.04,0.06)，η=（0.3,0.4,0.3），ρ=(-0.6,-0.4,-0.25),b=(0.05,0.03,0.02),β1～N[0.25,2.25]β2、β3～N(0,0.52)。对角分块矩阵Γ的主对角线元素（方差）均匀的产生于[0.05,0.20]，Γ中每块矩阵的协方差元素是从均匀分布U[0.1,0.5]中抽样获取的。

（4）在本文的研究中，选择资产维度分别为d=300、400、500，因子的个数分别为r=3。无论资产的维度是多少，对角分块矩阵Γ都被等额的分成了10块。

（5）重复上述步骤N次（N=100）。得到模拟数据后，在采用新提出的估计量估计协方差阵时，最优主成分的数目是与模拟研究中因子r的数目是一致的。大量研究认为采用稀疏抽样法有助于剔除市场微观结构噪声的影响，为此本文采用了抽样频率分别为30秒、1分钟、5分钟、15分钟、30分钟的数据来估计其协方差阵。

2．2　协方差阵估计量的比较

由AÏt-Sahalia和Xiu等的研究知：本文产生的模拟数据的积分协方差阵为：

其中，β是d×r的矩阵，E是d×d的单位矩阵，Γ是对角分块矩阵。分别采用和（样本协方差阵）估计模拟数据的协方差阵。然后，采用MSE损失函数来比较估计的协方差阵和积分协方差阵：

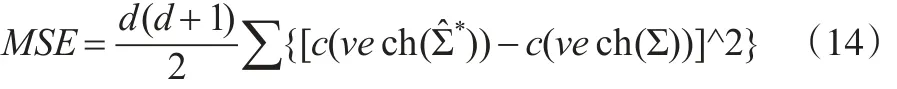
从表1不难发现两点：首先，无论样本量是多少，相较于传统的样本协方差阵估计量，本文提出的估计量所对应的MSE的均值最小，说明估计量的估计效果更好，比较接近于真实的积分协方差阵Σ。其次，抽样频率会明显的影响到协方差阵的估计效果，当抽样频率为15分钟时，较好的减弱了市场微观结构噪声的影响，协方差阵的估计效果较好。

表1　和估计量对应的MSE均值的比较

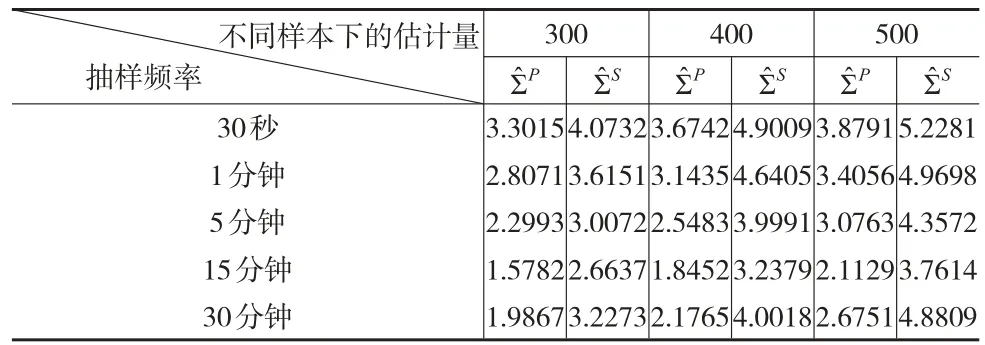
表1　和估计量对应的MSE均值的比较

3　实证分析

3．1　残差协方差阵的稀疏性分析

本文选择上证180指数成分股进行实证研究，抽取数据的时间跨度为2011年1月4日至2014年9月30日，将数据进行初步筛选，交易缺失数据被剔除后，所获得的样本数据量为906天。根据马丹、刘丽萍(2012)[11]的研究，180支股票可以被划分到8个板块中，这8个板块分别为：采掘业、交通运输和仓库业、制造业、信息技术业电力业、金融和保险业、煤气及水的生产和供应业、房地产业、综合业。

在采用高频数据来估计180支股票的协方差阵时，时间窗宽是1个月，那么本文所选的样本共45个月。采样频率为15分钟，鉴于我国股票的交易时间从上午09：30至11：30，下午13：00至15：00，所以每天会有16个观测值，那么每个月的样本量为22*16=352。分别采用本文提出的和样本协方差阵来估计每月的协方差阵，并对45个月的以及残差协方差阵分别进行加总分析。

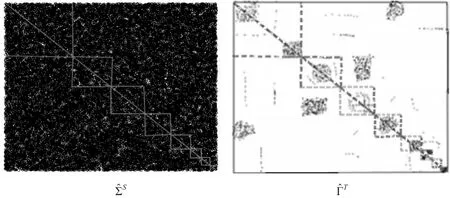
图1 和残差协方差阵的稀疏性分析

图1中所有的点都大于0.15，小于0.15的则替换为0，图中虚线围起的8个方块为上证180股票所分属的8个板块所构成的对角分块矩阵。根据图1得出两条结论：首先，没有提取任何主成分，而直接采用前文式（2）的样本协方差阵估计的的元素几乎全部大于0.15，图中的点非常密集，这说明不同资产间的相关性较为明显，反驳了Tao和Wang等（2013）[12]研究，认为直接采用门限函数等方法对资产的协方差阵进行稀疏处理并不合理；其次，对于提取了3个主成分并将门限函数应用到协方差阵的估计中后，得到的残差协方差阵，大于0.15的数据点主要集中在8个板块内，说明同一行业的资产之间的相关性较强，本文提出的协方差阵的残差协方差阵是对角分块矩阵，它不同于传统的对角残差协方差阵，其充分考虑了行业之间的相关性，使得协方差阵的估计更加有效。

3．2　协方差阵在投资组合中的应用研究

在本文的研究中，主要构造了两种类型的投资组合：等比例风险投资组合[13]以及最小方差投资组合。在这两种类型的投资组合中，较为常见的是最小方差投资组合，不再赘述。与最小方差投资组合的原理类似，等比例风险投资组合根据资产所占的风险比例来不断的调整权数，使每个资产所占的风险比例相同。在不允许资本市场卖空的条件下，其组合权数根据下式得到：

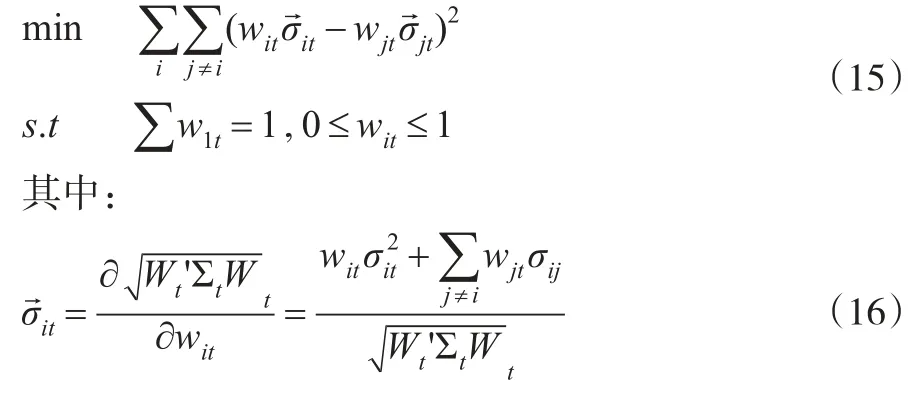
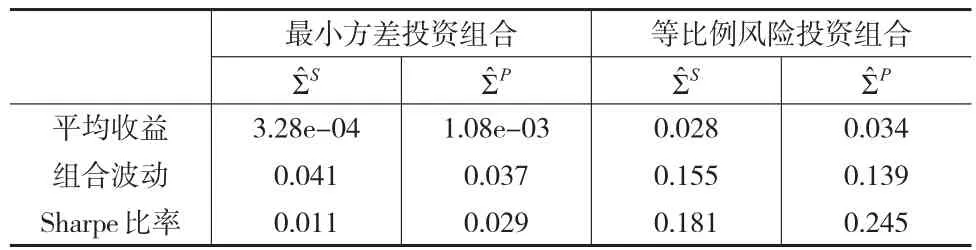
表2　不同投资组合的平均收益、组合波动和sharpe比率

4　结论

由于高频数据包含了丰富的市场信息，就高频协方差阵的估计问题已经引起了一些学者的关注，但大都是针对低维度的，基于高频数据的大维协方差阵估计仍然存在着诸多困难。针对目前研究的不足，本文将主成分分析法和门限方法应用到高频数据协方差阵的估计中，提出了新的协方差阵估计方法。该方法通过提取少数几个最优的主成分来刻画协方差阵的主要信息，解决维数诅咒问题；通过将门限方法应用到残差协方差阵中，来剔除噪声的影响。需要注意的是：本文引入的门限函数不同于传统的软门限函数或硬门限函数，而是考虑了同一行业的资产之间的相关性，得到残差协方差阵是对角分块矩阵。客观而言，同一行业不同资产间的协方差元素替换为0并不合理，因而对角分块残差协方差阵更为合理。通过模拟和实证研究发现：较传统的样本协方差阵估计方法，有效的提高了大维协方差阵的估计效率，其在投资组合中的应用效果更好。

参考文献：

[1]Andersen T G,Bollerslev T,Diebold F X,et al.Modeling and Forecasting Realized Volatility[J].Journal of Econometrica,2003,71(2).

[2]Zhang L.Estimating Covariation:Epps Effect,Microstructure Noise[J].Journal of Econometrics,2011,160(1).

[3]Barndor-Nielsen O E,Hansen P R,Lunde A,et al.Multivariate Realised Kernels:Consistent Positive Semi-definite Estimators of the Covariation of Equity Prices With Noise and Non-synchronous Trading[J].Journal of Econometrics,2011,162(2).

[4]Christensen K,Kinnebrock S,Podolskij M.Pre-averaging Estimators of the Ex-post Covariance Matrix Noisy Diffusion Models With Non-synchronous Data[J].Journal of Econometrics,2010,159(1).

[5]Fan J,Furger A,Xiu D.Incorporating Global Industrial Classification Standard Into Portfolio Allocation:A Simple Factor-Based Large Covariance Matrix Estimator With High Frequency Data[J].Journal of Business&Economic Statistics,2015.

[6]Antoniadis A,Fan J.Regularization of Wavelet Approximations[J].Journal of American Statistical Association,2001,(96).

[7]AÏt-Sahalia Y,Xiu D.Principal Component Estimation of a Large Covariance Matrix With High-Frequency Data[EB/OL].http://www.tse-fr.eu/sites/default/files/TSE/documents/sem2015/eee/xiu.pdf.

[8]刘丽萍,马丹,白万平.大维数据的动态条件协方差阵的估计及其应用[J].统计研究,2016,32(6).

[9]Cai T,Liu W.Adaptive Thresholding for Sparse Covariance Matrix Estimation[J].Journal of the American Statistical Association,2011,(106).

[10]Fan J,Liao Y,Mincheva M.Large Covariance Estimation by Thresholding Principal Orthogonal Complements[J].Journal of the Royal Statistical Society,2013,(75).

[11]马丹,刘丽萍.大规模高纬度金融资产的系统风险测量——基于动态条件异方差潜在因子模型的视角[J].数量经济技术经济研究,2012,(11).

[12]Tao M,Wang Y,Chen X.Fast Convergence Rates in Estimating Large Volatility Matrices Using High-Frequency Financial Data[J].Journal of Econometric Theory,2013,29(4).

[13]Maillard S,Roncalli T,Teiletche J.On the Properties of Equally Weighted Risk Contributions Portfolios[J].Journal of Portfolio Management,2010,(36).