采用低屈服点金属的可置换式钢节点减震分析*

2017-01-09何浩祥李瑞峰

振动、测试与诊断 2016年6期

关键词：梁端梁柱屈曲

何浩祥, 陈奎, 李瑞峰

(1．北京工业大学工程抗震与结构诊治北京市重点实验室北京，100124)(2．首都世界城市顺畅交通北京市协同创新中心北京，100124)

采用低屈服点金属的可置换式钢节点减震分析*

何浩祥1,2, 陈奎1, 李瑞峰1

(1．北京工业大学工程抗震与结构诊治北京市重点实验室北京，100124)(2．首都世界城市顺畅交通北京市协同创新中心北京，100124)

传统钢结构节点设计通常不能充分达到预期抗震要求，而以梁端削弱型梁柱节点虽然能够初步实现“强柱弱梁”，但可能在削弱区产生局部屈曲和整体侧移，在强震下安全储备不足。针对此问题，基于可恢复功能减震结构的理念，提出采用低屈服点金属的梁端削弱更换式梁柱节点。该节点利用低屈服点材料对翼缘和腹板的削弱处进行填补，在地震中低屈服点金属率先屈服并充分耗能，可降低节点主体的损伤，并可在震后对低屈服点金属进行更换。选取低屈服点钢材作为置换材料，通过材料性能试验获得相应的材料本构。在此基础上，对比分析低周往复加载下不同的抗震减震性能和损伤特征。采用多尺度有限元建模方式对采用不同类型节点的钢框架进行弹塑性时程分析。结果表明，可置换式节点能够将主要损伤控制在置换材料内，并具有更强的耗能能力、可恢复能力和安全储备。

耗能减震；低屈服点金属；多尺度模型；可置换节点；局部屈曲

引言

在多高层钢结构框架抗震设计中，梁柱节点的连接形式和耗能能力占有重要的地位，直接关系到钢结构整体的安全性和可靠性。目前，钢结构梁柱节点通常采用柱贯通型连接，典型梁柱刚性节点构造形式为钢梁翼缘与柱焊接、钢梁腹板与柱焊接或高强度螺栓连接。早期的钢节点设计假定翼缘连接承受全部弯矩而梁腹板只承受全部剪力，然而该连接的抗弯承载力只有梁本身抗弯承载力的80%左右，违背了抗震设计中“强节点弱构件”的基本原则[1-3]。在1994年美国北岭地震和1995年日本阪神地震中，多个钢结构房屋梁柱刚性连接节点脆性断裂的现象使设计者意识到传统刚性节点设计并未充分达到预期的抗震设计要求[4]。由此，各国学者提出了多种改进方法，其中塑性铰外移法成为研究热点，该法力图将梁的应力集中区从节点附近向外偏移，避免脆性破坏的发生，主要包括梁端削弱和梁端加强两种方式[5]。

狗骨型节点和腹板开洞型节点是梁端削弱式梁柱节点的典型代表[5-6]，两者均针对普通节点塑性区较小的不足，分别通过对钢梁的翼缘和腹板进行合理的削弱，使得梁体在地震时能够产生一定长度的塑性铰从而充分耗能, 实现延性设计。然而，梁端削弱式节点也存在以下不足：a.当翼缘或腹板被削弱后，构件整体刚度会降低，设计不当将存在安全隐患；b.在大震作用下削弱处将存在较严重的累积塑性应变并可能发生严重屈曲和侧向偏移，如果有余震产生，钢梁将发生二次损伤从而彻底破坏；c.局部削弱式节点在地震之后的修复技术复杂，成本较高。

近年来，可恢复功能结构(resilient structure)的理念应运而生并不断发展。可恢复功能结构是指地震后不需修复或稍加修复即可恢复其使用功能的结构，从结构形式上有多种实现方法[7-8]，但由于土木工程结构设计和施工技术的复杂性，目前在土木工程领域的实际应用还很少，国内外关于钢结构构件在严重受损后可更换性方面的研究成果也较少[9-10]。鉴于此，并针对目前梁端削弱型钢框架梁柱节点的不足，笔者提出一种采用低屈服点金属的可置换式钢结构梁柱节点。该新型节点采用低屈服点的金属材料对钢梁的翼缘和腹板削弱处进行填补，在地震时低屈服点金属率先进入变形并充分耗能，能够提高节点整体抗震性能。此外，通过合理地设置削弱和填补尺寸，可以将累积塑性应变基本控制在低屈服点金属内，避免梁和节点出现较大变形，从而在震后可以快速简便地完成节点修复工作，体现了可恢复功能结构的思想。

在评价不同钢结构梁柱节点抗震减震性能时，除了采用低周往复加载试验或模拟分析外，也应重视地震作用下节点在框架整体振动中的性能，一般可采用非线性动力时程分析方法。目前，常用的工程非线性分析主要包括基于宏观单元的整体分析和基于实体单元的局部分析。宏观模型主要采用杆、壳等单元，计算量虽然小，但不能完整地反映结构破坏的微观机理，如结构的局部失稳、节点破坏及接触问题等。基于实体单元的精细分析，虽然可以较好地模拟结构的局部破坏过程，但计算量大，且易出现计算不收敛等现象[11-12]。多尺度模型主要对不同尺度的力学行为采用不同的单元进行模拟，进而组合成多尺度有限元模型，因此多尺度计算可在精度和计算代价之间达成一个较好的平衡点。近年来，国内外学者对采用多尺度分析中的界面的连接、约束条件设定等问题进行了深入研究，并采用多尺度建模方法对工程结构的静动力特性进行了深入分析，验证了多尺度分析的精确性和有效性[11-14]。笔者选择LY160钢材作为可置换式节点使用的低屈服点金属材料，通过材料性能试验获得相应的材料本构曲线。在此基础上利用有限元软件分析了低周往复加载下传统节点、梁端削弱型节点和可置换式节点的抗震减震性能，并对比了不同节点的耗能能力和局部屈曲特征。最后采用多尺度有限元建模方式对具有不同类型节点的钢框架进行了地震弹塑性时程分析，验证了可置换式节点在抗震减震方面具有优越性。

1 采用低屈服点金属的可置换式节点

目前常见的梁端削弱式梁柱节点分为两种，梁端翼缘削弱型和梁腹板削弱型，具体构造如图1所示。可依据文献[15]确定梁翼缘削弱参数，假定bf和hb分别为梁的翼缘宽度和梁截面高度，其中削弱起始点至柱面距离a可取为0.50bf～0.75bf，削弱长度b可取为0.65hb～0.85hb，削弱深度c可取为0.20bf～0.25bf，圆孔半径R可取为0.25hb～0.375hb。

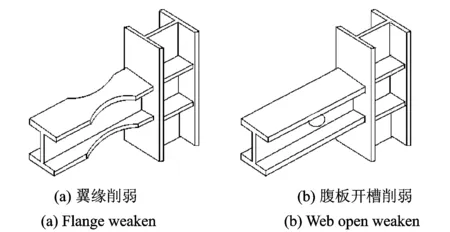
图1 梁端削弱型钢节点Fig.1 Beam end weaken steel connection

针对梁端削弱式节点在罕遇地震下可能出现严重屈曲和梁体侧向偏移的不足，笔者提出采用低屈服点金属的梁端更换式梁柱节点，其构造如图2所示。该节点借鉴削弱型节点的构造，但是为了在保证结构承载力的前提下更好地体现低屈服点材料的性能，首先削弱和去除钢梁端部翼缘和腹板的部分原有钢材，之后通过焊接等方式将削弱部分更换为屈服点较低并且耗能能力强的金属材料。为了充分发挥低屈服点金属的耗能能力，建议相应的削弱参数取传统削弱式节点取值范围中的较大值。在地震中，低屈服点金属材料率先进入变形并达到屈服阶段，从而形成梁端塑性铰进行耗能减震，而节点原有部分不产生严重的塑性变形，保证节点整体抗震性能。主震作用后，可迅速更换低屈服点金属使节点整体抗震性能得到恢复，使钢结构节点和框架整体具备抵抗余震的能力。

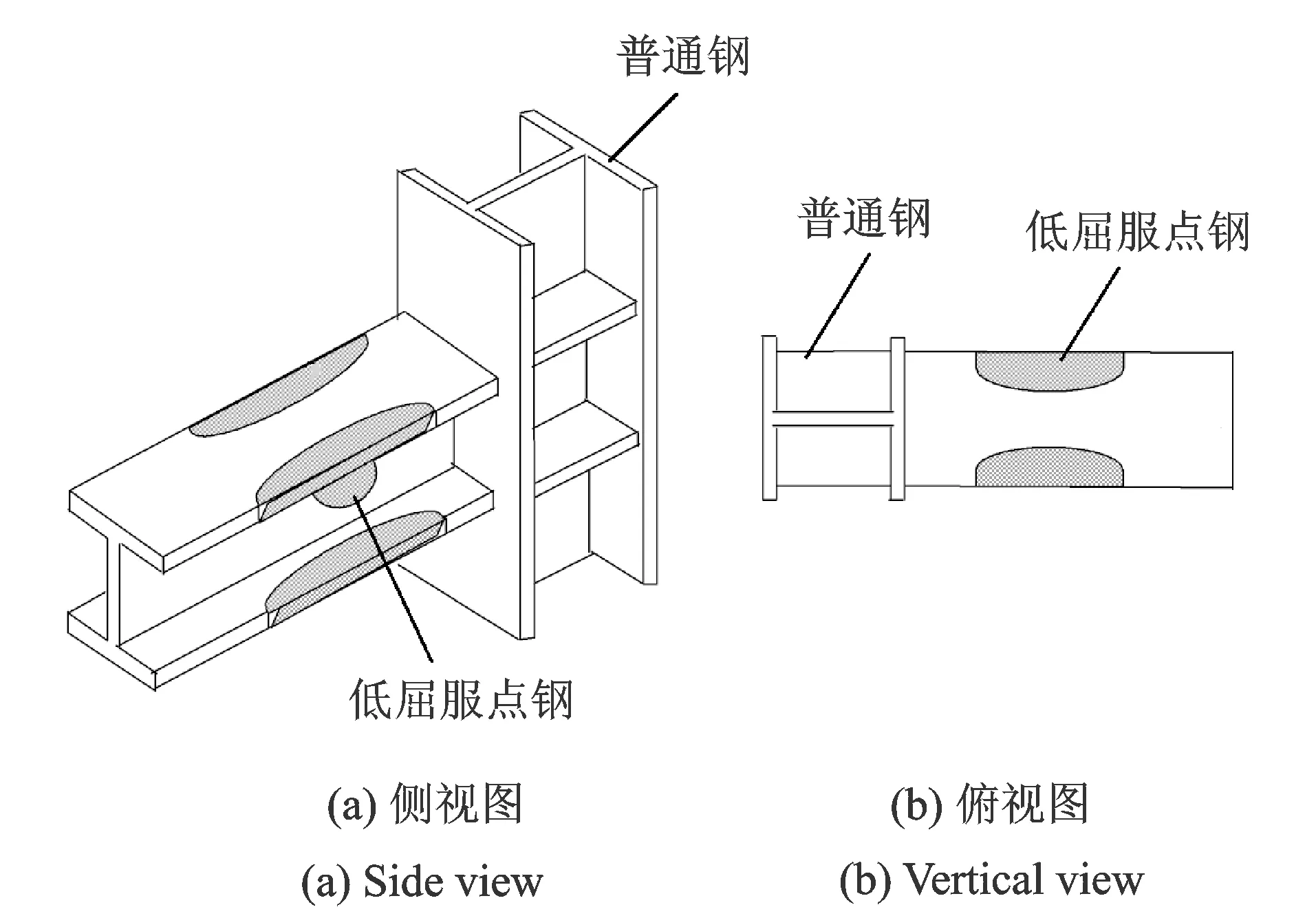
图2 梁端削弱更换式钢框架梁柱抗震节点Fig.2 Beam end weaken replaceable connection

2 低屈服点金属的材料性能

梁端削弱式节点减震作用的关键技术之一是选取具有较低屈服强度和延伸率的耗能材料。目前国内外关于利用低屈服点金属进行减震的理论研究较多，但能够达到工程应用的材料较少[16-17]。笔者选择国产低屈服点钢LY160(屈服点约为160 MPa)作为低屈服点耗能材料。为了获取并对比不同钢材的真实材料性能参数，选用Q345钢、Q235钢以及LY160钢3种材料并分别加工制作了3个相同拉伸试验尺寸的试件，根据文献[18]的方法进行试验，通过试验测得每组的平均值作为最终结果。

标准试件尺寸、拉伸试验现场及不同材料试件断裂后的图片如图3所示。3种钢材各自的平均应力应变曲线如图4所示。从拉伸试验的应力应变曲线中可以得到：Q345钢、Q235钢和LY160钢的实测屈服强度分别为385,275和160 MPa；实测延伸率分别为23%,27%和31%。通过以上数据可以认为，LY160钢具有预期的低屈服点以及优良的延展性和韧性，能够在较大变形下充分耗能，且保证结构的承载力不发生较大变化，保证结构主体的稳定性，因此作为可置换式钢节点的低屈服点材料进行使用。

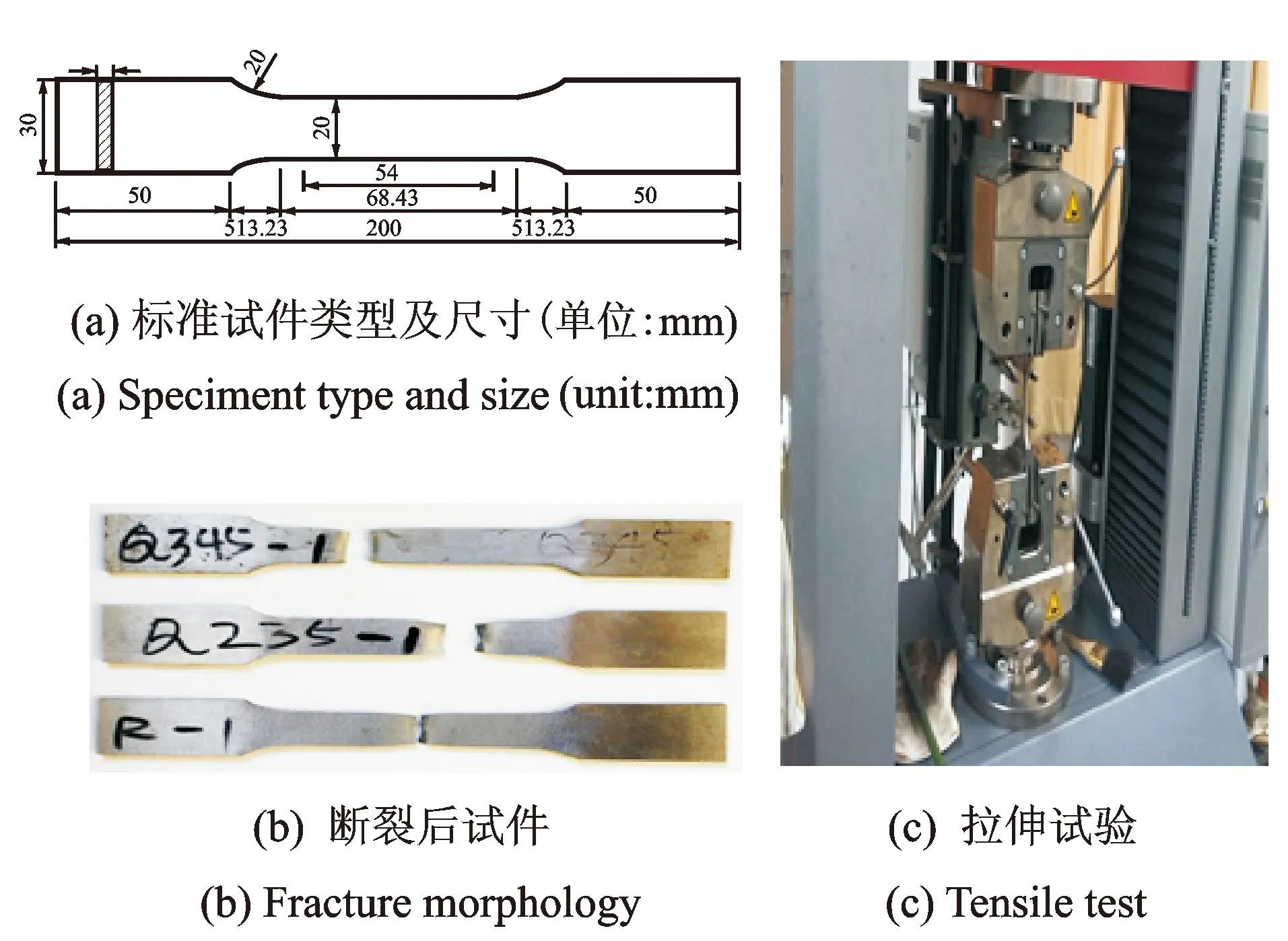
图3 试件尺寸、拉伸试验和断裂形态Fig.3 Specimen size tensile test and fracture morphology

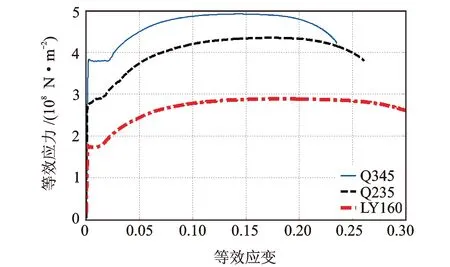
图4 不同钢材的本构曲线Fig.4 Constitutive curve of different steel

3 可置换式钢节点减震性能模拟

为了验证采用低屈服点金属的可置换式的钢节点的减震性能，笔者利用ANSYS有限元软件分别建立传统梁柱节点、腹板开洞和翼缘削弱式梁柱节点及可置换低屈服点金属的梁柱节点模型，并进行了低周往复加载下的非线性分析，从而对节点的滞回耗能能力进行研究。节点模型的梁和柱均采用H型钢，主体材料为Q345钢，低屈服点金属为LY160钢。柱子截面的尺寸为HW450 mm×300 mm×20 mm×12 mm，梁截面的尺寸为HN400 mm×200 mm×12 mm×12 mm。削弱型节点的尺寸参数在上文提及的取值范围中选择，参见表1。同时，为了对比分析不同置换尺寸下的梁柱节点对结构抗震性能的影响，选择3种不同置换尺寸，参数也如表1所示。

表1 削弱和置换尺寸

在各节点的柱两端施加固定约束，梁端施加位移约束并进行循环往复荷载，采用位移增量控制。初始状态为0，逐步加载，位移增量步长为每级12 mm，每级循环2次，总12级，直到构件屈曲破坏。梁端加载位移达到144 mm时，不同类型的节点等效应力图如图5～图7所示。

由以上结果可以看出，达到极限位移时，传统节点的应力极值集中在梁端部与柱连接处，梁端形成塑性铰发生明显局部屈曲，受损后的维修不便。削弱式梁柱节点的塑性铰外移到梁上削弱处，在削弱处产生了严重的局部屈曲和侧向大变形，表明节点已经发生较严重破坏，抗震能力不能满足要求。可置换式节点的变形和传统节点比较接近，但塑性铰外移到置换金属处，其局部屈曲和耗能主要发生在低屈服点置换材料内部，而主体材料的破坏相对较小，在损伤后将低屈服点材料置换后仍然具备足够的抗震能力和可恢复能力。不同梁柱节点的滞回曲线如图8所示。可以看出，可置换式节点和传统节点的滞回环比较饱满，而削弱式梁柱节点的滞回环面积明显减小，且后期承载力下降较快，耗能能力明显不足。

图5 传统梁柱节点应力云图Fig.5 Stress of traditional beam-column connection

图6 削弱式梁柱节点应力云图 Fig.6 Stress of beam-weaken connection

图7 可置换金属梁柱节点应力云图Fig.7 Stress of replaceable connection

图8 不同梁柱节点的滞回曲线比较Fig.8 Hysteresis curves of different connections

为了更直观地比较不同类型节点的耗能能力，选用等效滞回阻尼比以及Park-Ang损伤指数[19]计算模型来分别考虑不同节点在低周往复荷载下的性能。

等效滞回阻尼比ξ为

(1)

其中：ED为结构单周期运动滞回阻尼耗能，等于滞回环包围的面积；ES为最大应变能。

Park-Ang损伤指数DI为

(2)

其中:xcu为构件在单调加载下的极限位移；Fy为构件的屈服强度；xm和Eh为构件实际的地震最大变形和累积滞变耗能；β为构件耗能因子，本研究按照0.15取值。

计算各节点在不同位移下的等效滞回阻尼比曲线和Park-Ang损伤指数曲线，分别如图9和图10所示。从图中可以看出,在低周往复加载下，传统节点的等效滞回阻尼比增长相对缓慢，在节点发生较大变形时相对稳定，但此时损伤指数急剧增长，表明传统节点的滞回耗能能力和延性均较低，损伤较严重。虽然削弱式节点的等效滞回阻尼比传统节点的大，后期已经达到了0.45以上，有较强的耗能能力和延性，但是通过损伤指数可以看出削弱节点损伤最为严重，过早出现了局部屈曲破坏并丧失了承载能力。3个置换式节点的等效滞回阻尼比随着滞回次数稳定而快速地增长，后期均达到了0.45。置换式节点损伤指数在位移较小时大于传统节点的指数，但随着位移的增加其增速变缓，在位移较大时已小于传统节点的。这表明在往复加载下置换式节点由于低屈服点钢材先屈服而进行充分耗能，由于低屈服点钢材具有良好的延伸率，因而置换式节点在后期损伤相对较小，仍能保持完整性。

图9 不同节点的等效阻尼比对比Fig.9 Equivalent damping ratio of different connections

图10 不同节点的损伤指数对比Fig.10 Damage index of different connections

综上所述，可置换节点比传统节点具有更好的延性耗能能力，并且可以使塑性铰外移到梁上，避免在梁柱节点处形成塑性铰使结构发生脆性断裂破坏。此外，在低屈服点金属发生屈曲变形后可进行置换，防止余震下的结构破坏。狗骨式节点虽然能够使塑性铰外移到梁上削弱部位，但其承载力下降比较明显，在削弱处易产生应力集中和屈曲变形，并且后期延性耗能能力比较差。因此，可置换梁柱节点具有比其他两种节点更好的抗震性能。

为了比较不同置换尺寸对节点性能的影响，对3种置换式梁柱节点采用相同位移控制的低周往复加载。在梁端进入到弹塑性变形时，不同置换尺寸下的梁柱节点均在置换部位产生了屈曲变形，3种尺寸下的承载能力基本相同。笔者采用置换节点2进行后续研究。

4 基于多尺度的减震钢框架性能分析

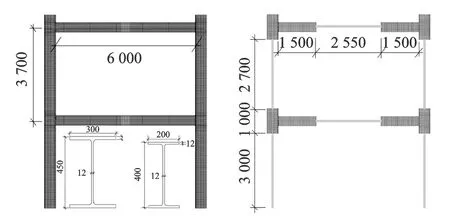
图11 全实体和多尺度模型及尺寸(单位：mm)Fig.11 All entities and multi-scale models and section size(unit:mm)

为了研究采用不同类型节点的钢框架结构在地震作用下的动力性能，笔者利用有限元分析软件ANSYS对两层钢框架结构进行地震动下的弹塑性时程分析。结构和详细尺寸如图11所示。有限元模拟中轴压比为0.3，附加质量为1.6t。由于全实体建模计算效率低，因此对多尺度建模和分析的效果进行了研究，同时建立了全实体模型和多尺度模型。在全实体模型中，梁柱均选用SOLID95实体单元；在多尺度模型中，梁柱节点部分选用SOLID95实体单元；其他部位选用BEAM188梁单元。不同单元之间通过建立约束方程和定义刚性连接区来模拟实际连接，确保了模拟精度。

采用El Centro波作为地震动进行时程分析，加速度峰值调幅至为0.70g，持续时间取16 s。在相同网格尺度划分精度下，全实体模型和多尺度模型的顶部位移时程曲线如图12所示，二者结果十分接近。以上结果表明，采用多尺度模型进行静力和动力分析均具有令人满意的精度。时程分析中采用全实体模型计算耗时为3 417 min，而采用多尺度模型计算耗时仅为1 512 min，可见多尺度分析在计算效率上具有明显优势。

图12 地震下顶部位移响应Fig.12 Displacement history of top floor

时程分析中地震动幅值达到峰值时，传统梁柱节点式框架、狗骨节点式框架以及置换节点式框架结构的节点底部局部应力云图如图13～图15所示。可以看出，传统节点在梁柱连接处应力达到最大值。削弱节点在翼缘削弱处和腹板开洞处发生应力集中，并且在削弱处发生较大的横向屈曲变形，而置换低屈服点金属的钢框架节点处应力值分布较均匀，与传统节点相比节点核心区处的应力出现了有效降低，更利于抵抗罕遇地震。

图13 传统节点下框架节点处应力云图Fig.13 Stress of frame with traditional connection

图14 削弱节点下框架节点处应力云图 Fig.14 Stress of frame with weaken connection

图15 置换节点下框架节点处最大应力云图Fig.15 Stress of frame with replaceable connection

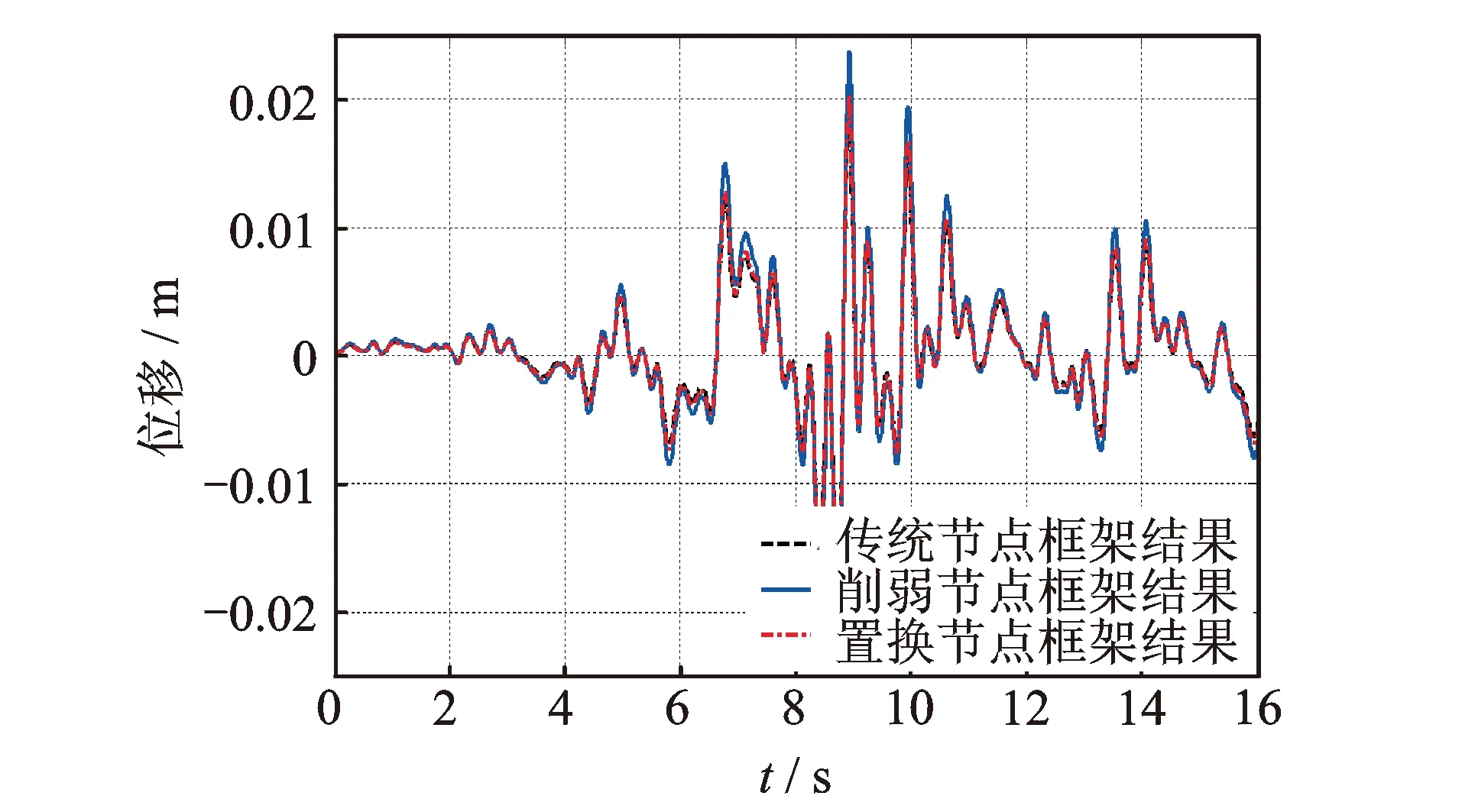
图16 顶部位移时程曲线Fig.16 Displacement history of top floor

不同框架的顶部位移时程曲线如图16所示，其中削弱式梁柱节点钢框架结构顶部位移幅值最大，达到0.028 m。采用可置换式节点的钢框架顶部位移和传统框架的顶部位移基本相同，均为0.02 m。综合可以看出：采用削弱节点的框架的顶部位移反应和最大应力值均最大；采用置换节点的框架与传统钢框架相比整体变形和局部应力分别区别并不明显，然而其具有较强的安全储备和震后可恢复功能，因而适合在今后的钢结构设计和应用中适当推广。

5 结束语

在地震作用下，梁端削弱式梁柱节点能够将塑性铰外移，并进行充分的耗能，实现延性设计。然而，梁端削弱式节点可能发生局部屈曲和侧向偏移，设计不当将存在安全隐患，同时不利于震后加固。针对上述不足，笔者提出了采用低屈服点金属的可置换式钢结构梁柱节点。该新型节点采用低屈服点的金属材料对钢梁的翼缘和腹板削弱处进行填补，在地震时低屈服点金属率先进入变形并充分耗能，能够提高节点整体抗震性能。同时该节点可以在震后进行快速有效地置换，符合可恢复功能结构的理念。

笔者对包括低屈服点钢在内的不同强度的钢材进行了拉伸试验，得到了各自的本构关系。在此基础上，利用有限元软件分析了低周往复加载下传统节点、梁端削弱型节点和可置换式节点的抗震减震性能。结果表明，可置换式节点具有良好且稳定的耗能能力，不易造成节点主体的局部屈曲和侧向变形，同时具有易于置换和加固的优点。为了对比分析结构整体抗震减震能力，笔者采用多尺度有限元建模方式对具有不同类型节点的钢框架进行了地震弹塑性时程分析。结果表明，采用可置换式梁柱节点的钢结构在地震作用下位移较小，在利用低屈服点钢材进行充分耗能的同时保证了主体结构的安全，且易于维修，如经济方面允许，可在工程中应用。与全实体模型相比，多尺度有限元模型可以准确模拟梁柱节点的应力状态和结构整体动力响应，并在保证计算精度的同时明显提高了计算效率，适合在设计和分析中推广。

[1] Chen Shengjin, Chao Y C. Effect of composite action on seismic performance of steel moment connections with reduced beam sections [J]. Journal of Constructional Steel Research, 2001, 57(4): 417-434.

[2] Popov E P, Blondet M, Stepanov L. Application of dog bones for improvement of seismic behavior of steel connections [R]∥ ERRC Report. San Francisco:University of California,Berkeley,1996.

[3] Popov E P, Yang T S, Chang S P. Design of steel MRF connections before and after 1994 Northridge Earthquake [J]. Engineering Structures, 1998, 20(12): 1030-1038.

[4] 李波, 杨庆山, 杨娜, 等. 采用腹板开圆孔梁柱节点的钢框架足尺模型抗震性能研究[J].建筑结构学报, 2007, 28(6):160-166.

Li Bo, Yang Qingshan, Yang Na, et al. Experimental research on aseismic behavior of steel moment-resisting frame with opening on beam web [J]. Journal of Building Structures, 2007, 28(6):160-166. (in Chinese)

[5] 石永久, 王萌, 王元清. 不同焊接节点构造形式钢框架整体抗震性能分析[J]. 工程力学, 2012, 29(11): 71-79.

Shi Yongjiu, Wang Meng, Wang Yuanqing. Analysis on seismic behavior of overall steel frame with different welded connection constructions[J]. Engineering Mechanics,2012, 29(11): 71-79. (in Chinese)

[6] FEMA-350 Recommended seismic design criteria for new steel moment frame buildings[S]. Washington DC: SAC Joint Venture,2000.

[7] 吕西林, 陈云, 毛苑君.结构抗震设计的新概念——可恢复结构[J]. 同济大学学报,2011,39(7): 941-948.

Lü Xilin, Chen Yun, Mao Yuanjun. New concept of structural seismic design:earthquake resilient structures[J]. Journal of Tongji University,2011,39(9):941-948. (in Chinese)

[8] 吕西林, 陈聪. 带有可更换构件的结构体系研究进展[J].地震工程与工程振动, 2014, 34(1): 27-36.

Lü Xilin, Chen Cong. Research progress in structural systems with replaceable members[J]. Earthquake Engineering and Engineering Dynamics, 2014, 34(1):27-36. (in Chinese)

[9] Farrokhi H, Danesh F, Eshghi S. A modified moment resisting connection for ductile steel frames (Numerical and experimental investigatior) [J]. Journal of Constructional Steel Research, 2009, 65(10-11): 2040-2049.

[10]Oh S H, Kim Y J, Ryu H S. Seismic performance of steel structures with slit dampers [J]. Engineering Structures, 2009, 31 (9): 1997-2008.

[11]Ladeveze P. A multiscale computational approach for contact problem[J].Computer Methods in Applied Mechanics and Engineering,2002,191(43):4869-4891.

[12]Li Zhaoxia, Zhou Taiquan, Chan T HT, et al. Multi-scale numerical analysis on dynamic response and local damage in long-span bridges[J]. Engineering Structures, 2007, 29(7): 1507-1524.

[13]林旭川, 陆新征, 叶列平. 钢-混凝土混合框架结构多尺度分析及其建模方法[J].计算力学学报, 2010, 27(3): 469-475.

Lin Xuchuan, Lu Xinzheng, Ye Lieping. Multi-scale finite element modeling and its application in the analysis of a steel-concrete hybrid frame [J]. Chinese Jour-

nal of Computational Mechanics, 2010, 27(3): 469-475. (in Chinese)

[14]石永久, 王萌, 王元清. 基于多尺度模型的钢框架抗震性能分析[J]. 工程力学, 2011, 28(12): 20-26.

Shi Yongjiu, Wang Meng, Wang Yuanqing. Analysis on seismic behavior of steel frame under multi-scale calculation method [J]. Engineering Mechanics, 2011, 28(12): 20-26. (in Chinese)

[15]郁有升,王燕. 钢框架梁翼缘削弱型节点力学性能的试验研究[J]. 工程力学, 2009, 26(2): 168-175.

Yu Yousheng, Wang Yan. Experimental study on the mechanical property of reduced beam section connections of steel frames[J]. Engineering Mechanics, 2009, 26(2):168-175. (in Chinese)

[16]李钢, 李宏男. 装有“双功能”软钢阻尼器框架结构振动台试验与分析[J]. 振动与冲击, 2010, 29(8): 164-168.

Li Gang, Li Hongnan. Shaking table experiment of frame structure with dual functions metallic damper [J]. Journal of Vibration and Shock, 2010, 29(8): 164-168. (in Chinese)

[17]田洁, 颜智超, 卢俊龙. 极低屈服点钢在密肋壁板结构中的减震控制研究[J].振动与冲击, 2014, 33(5): 160-164.

Tian Jie, Yan Zhichao, Lu Junlong. Aseismic control of a multi-ribbed slab structure using ultra low yield strength steel [J]. Journal of Vibration and Shock, 2014, 33(5): 160-164. (in Chinese)

[18]GB /T 228.1-2010 金属材料拉伸试验第1部分: 室温试验方法[S]. 北京:中国标准出版社, 2011.

[19]Park Y, Ang A H S, Wen Y K. Seismic damage analysis of reinforced concrete buildings[J]. Journal of Structural Engineering,1985, 111(4): 740-757.