让学生思维“卷入”错题思考——由在线“个别答疑、辅导”说起

☉江苏省泰州市姜堰区娄庄中学 朱金祥

让学生思维“卷入”错题思考
——由在线“个别答疑、辅导”说起

☉江苏省泰州市姜堰区娄庄中学 朱金祥

近年来，教师的答疑方式从传统的面对面解惑，拓展到学生在家做作业时，由家长转达学生的作业或疑难问题，通过QQ或微信方式跟老师进行交流.然而我们见到的较多的答疑方式仍然是答案告知式的低层次答疑方式，一些在数学方面适应偏弱的学生，常常羞于反复询问思路，或不主动思考自己的错误原因，不能从纠错走向究错，使得这种答疑的效果大打折扣，长久下去，这类学生也不能坚持提问，不敢提问，使得在线个别辅导或答疑渐渐冷淡下去.笔者整理新近开展的一些九年级典型案例，并跟进阐释一些相关思考，供研讨.

一、“在线答疑”案例展示

案例1：二次函数y=x2-3x+2的图像与x轴的交点坐标是？与y轴的交点坐标是？

答疑预设PPT：（为了真实、生动、形象地展示我们答疑过程的原生态素材，以PPT截图的方式呈现，下同）

图1

案例解读：从学生的错误可见，他还是懂抛物线与x轴交点的求法的，但是与y轴的交点不会求，至少说明他在八年级对一次函数图像与y轴交点就掌握得不好，因为它们本质上是一致的.这就是我们在预设PPT点拨的最后，提出了“关联：与直线y=kx+b与x、y轴交点坐标一起理解”的跟进思考.目的是不仅让学生订正一个答案，而且要把一类问题都弄通、关联起来理解，理解有些函数问题存在前后一致性.

案例2：二次函数y=x2-2x+1与坐标轴的交点个数是（）.

A.0 B.1 C.2 D.3

答疑预设PPT：

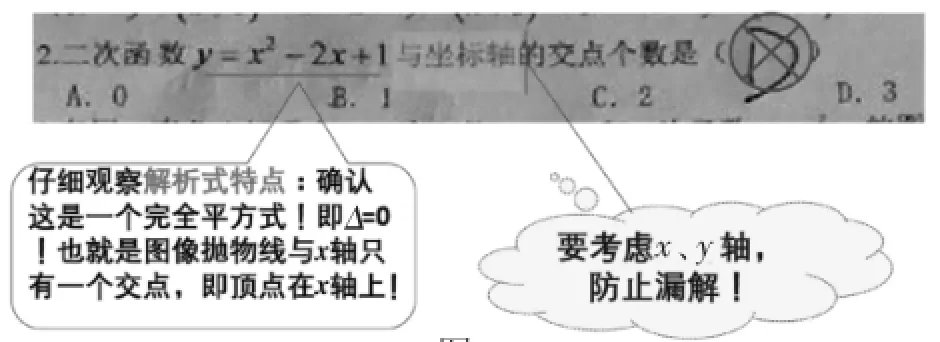
图2

案例解读：该生错选D，说明已考虑两条坐标轴，但是没有注意该解析式是一个完全平方式，或者对完全平方式不够敏感，或者对解析式为完全平方式时与“根的判别式”之间的对应关系理解不到位，没有能对应到此时“顶点恰在x轴上”这些等价命题.

案例3：抛物线y=3x2向右平移1个单位，再向下平移2个单位，所得的抛物线是（）.

A.y=3（x-1）2-2 B.y=3（x+1）2-2

C.y=3（x+1）2-2 D.y=3（x-1）2+2

答疑预设PPT：

图3

案例解读：该学生记错抛物线平移带来的系数变化，是一处知识漏洞.如果简单修补答案也是可以的，但不能达到对这个问题的深刻理解.故预设了两个“标注”引导他自主发现错漏，并有选择性地记忆口诀（为了便于类比学习，同时提出了这类错解可以逆向验证，即对选项中抛物线进行逐个分析）、发现矛盾，从而再次确认解答.此外，我们不但给出抛物线平移的规律口诀，还对照给出抛物线对称轴与y轴位置关系的口诀“左同右异”，即抛物线对称轴在y轴左侧时，a、b同号；抛物线对称轴在y轴右侧时，a、b异号）.

案例4：（1）若将二次函数y＝x2-2x+3配方为y＝（x-h）2+ k的形式，则y＝_____.

（2）已知二次函数y＝x2+bx+3的对称轴为x＝2，则b＝_____.

答疑预设PPT：

图4

案例解读：这两道题对应在一起，说明该生基本掌握配方法，但是在较为繁杂的配方出现时，手忙脚乱，又出现了错误.如何避免这类“高位”错误呢？不能仅仅要求学生再仔细点，而应从不同的角度验证，比如把答案回代解析式，根据对称轴方程确认，或要求学生根据对称轴方程的公式求解，也就是别在原来的思路上“再做一次”.

案例5：已知，如图（略，见PPT截图），二次函数y＝ax2+ bx+c的图像与x轴交于A、B两点，其中A点坐标为（-1，0），点B坐标为（5，0），另抛物线经过点（1，8），M为它的顶点.

（1）求抛物线的解析式；

（2）求△MCB的面积S△MCB.

答疑预设PPT：

图5

案例解读：这是一道解答题，第（2）问其实与抛物线无关（学生已顺利解出抛物线解析式，且灵活地在顶点式、交点式、一般式之间转换变形），分离出问题后其实是已知平面直角坐标系中三个定点，求以它们为顶点构成的三角形的面积，方法多样.该同学添加出分割线CD也是可行的，但问题在于点D的坐标没有求出，就匆忙应用并代入计算，其间过程跳跃太多，所谓“十次算错九次快”，此亦一例.考虑到方法的多样性，利用分割法，由这个图形的特殊位置而言，选择PPT中指出的MN，会使得运算更为简化，因为点N是直线MN与BC的交点，而直线BC的解析式更容易求得甚至可直接“看”出：y＝-x+5.在这组PPT的答疑艺术中，既保护学生积极、合理的思考路径，又指出“别处风景更好”，让学生更容易自主修正，保护信心、提示优化.

二、关于“在线答疑”的进一步思考

1.理解错解并理解学生，是搞好在线答疑的前提

面对学生的提问，很多情况下学生都是鼓足了勇气提问的，所以面对错解不可简单否定、指责或批评，而应首先分析并理解读懂错解，分析具体学生的学情，理解他出现这类错误的合理性，这是搞好在线答疑的前提，也是一种扶持的情怀.

2.肯定错解中合理成分，保护信心并且获取信任

在理解学生的错解，评估和辨明他们出现错误的原因之后，预设PPT时首先要指出他们在解答中哪些步骤是正确的，哪些“念头”是积极的，值得鼓励的；按哪些思路走下去，如果不跳步骤是能到达目标的；哪些错误其实可以得到自主修正.我们在PPT备注时指出他们的合理成分，学生的信心得到保护，并且获取了他们的信任，学生也就愿意主动跟进订正，正如有些教师所谓的“骗”着学生心甘情愿地主动学习.

3.提示思路并预设互动，促使学生思维“卷”入题中

由于在线答疑“隔着”空间，不能像面对面那样观察学生的表面，故要想真正引发他们思考需要靠我们精心预设“提示语”，这也是取得高质量在线答疑、辅导的重要所在，也是我们需要认真修炼的专业基本功，以避免答疑走向答案告知的低层次辅导.上面列举的5个案例的PPT截图中的“提示句”基本做到了没有直接告知答案，而且通过一些追问和提示或思路对比，促使学生在这些提示句引导下，思维“卷”入题中，深入思考.顺便提及，上述题例经过辅导之后，都得到了家长的积极反馈，家长非常高兴他们的孩子根据提示思考后发现了思路的兴奋与愉悦.想来，自主发现思路的愉悦不仅让孩子获得了心理满足，家长也跟着高兴，这也算是一种“教育之乐”吧.

1.李祎.另眼看难点［J］.数学通报，2016，55（7）.

2.孙莉.思路生成贵在自然，一题一课追求简约——一道考题的思路突破与习题课设计［J］.中学数学（下），2016（9）.

3.郑毓信.善于举例［J］.人民教育，2008（18）.

4.郑毓信.善于提问［J］.人民教育，2008（19）.

5.吴忠妙.一道考题的思路、难点与教学设计［J］.中学数学（下），2016（9）.Z.