合情转化合理提炼适度变式——一道等腰三角形底角平分线的习题解答及思考

☉湖北省秭归县归州镇初级中学 叶先玖

合情转化合理提炼适度变式
——一道等腰三角形底角平分线的习题解答及思考

☉湖北省秭归县归州镇初级中学 叶先玖

以等腰三角形这一基本图形为载体，与角平分线相融合，可以借题发挥，生长出很多具有训练思维的题.本文以“等腰三角形底边、底角平分线及它分腰所成的线段”的数量关系为例，掌握“截长补短”证明线段和差数量关系的操作，并探讨习惯方法受阻时，怎么突破障碍，思考解题教学时，如何引导学生合情转化、合理提炼、适度变式，丰富解题经验，提升解题效率，希望得同仁的斧正.

一、题目呈现

如图1，△ABC中，AC=BC，∠C=100°，AD平分∠CAB交BC于D，求证：AD+CD=AB.

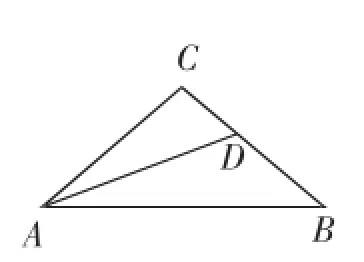
图1

解答本题时，最常见的是从所证结论AD+CD=AB出发，执果索因，利用截长补短这一常见的基本套路解决.那么，如何充分利用“AC=BC，∠C=100°，AD平分∠CAB”这些条件，执因索果，构图转化而获思路？由AC=BC，想到过C作AB边上的垂线，利用三线合一；由AD平分∠CAB想到向角的两边作垂线或作角的一边的平行线；由∠C=100°，能想到构建一些图等.学生解答时，却处处受阻而最终放弃.那么，这些常用方法和思路，是不是不能解决这道题？带着这些疑问，我与学生一道展开研讨，并收获了以下证法.

二、解法探讨

证法1：截长法构等腰三角形：考虑到所证结论AD+ CD=AB中，AB最长，所以在AB上取一段AF=AD得一个等腰三角形，再证BF=CD.

证明：如图2，取AF=AD，所以∠ADF=∠AFD.由AC= AB，∠C=100°.可得∠B=∠CAB=40°.又因为AD平分∠CAB，则∠DAB=20°.在△DAF中，由三角形内角和可得∠DAB+∠ADF+∠AFD=180°，从而得∠AFD=80°.因为∠AFD是△BDF的一个外角，所以∠AFD=∠B+∠BDF，从而可得∠B=∠FDB=40°，所以DF=BF.

再取AE=AC，连接DE.在△ACD和△AED中，由AC= AE，∠CAD=∠DAB，AD=AD，可证得△ACD≌△AED，则CD=DE，∠C=∠DEA=100°，从而有∠DEF=∠DFE= 80°，所以DE=DF，进而有CD=DE=DF=FB，所以AB=AF+ FB=AD+CD.

证法1是从结论中较长线段上截取一段和结论中某一段相等，然后想办法证明另一段和剩下的一段相等，这是一种解决类似线段和差问题常用的方法.然而为什么要这么做？换而言之，可不可以截取AF=CD或BF=CD，再证明余下的一段与AD相等？通过分析，证法1中其实是利用了∠CAD=∠DAB，且这两个等角共用一条边AD，即“等角共边可翻折”，从而顺利完成各线段之间的等量转化.

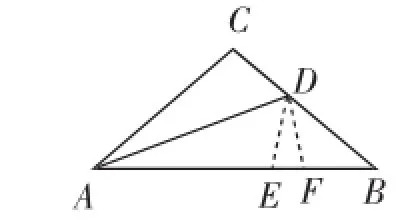
图2

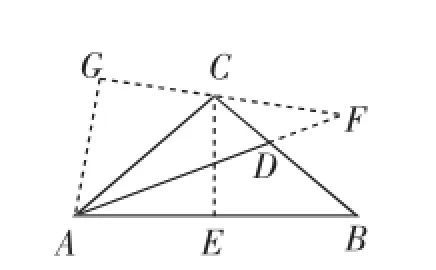
图3

证法2：补短构含30°角的直角三角形：既然证法1可行，那么，我们从较短的线段中选择一条，把另一条短线段，移到这条线段的延长线上，从而把两条短线段合成一段，只要证明它和结论中那条较长线段相等即可.

证明：如图3，延长AD到F，使得FD=CD，连接FC，作AG⊥FC于G，CE⊥AB于E.

由AC=BC，∠C=100°，得∠CAB=∠B=40°.又AD平分∠CAB，则∠DAB=20°，则∠ADB=120°，所以∠CDF= 120°.

因为CD=FD，从而∠F=30°.易得∠GAF=60°，从而∠GAC=∠CAE=40°.由∠G=∠AEC，∠GAC=∠EAC，AC=AC，得△ACG≌ACE，则AG=AE.AF.又 AE=

在△AGF中，由∠F=30°，∠G=90°，得AG= AB，从而AF=AB=AD+FD=AD+CD.

不难发现，AC正好是∠GAB的平分线，因此，证法2与证法1在思路上应都是基于“等角共边可翻折”构造，于是在上述截长补短法启示下，思构两次翻折，如图4，很自然得到证法3.

简证：如图4，沿AD翻折△ACD，即在AB上截取AE= AC；再将△BED沿BD翻折得△BFD，即延长AD到F，使AF=AB.易证得CD=DE=DF，AB=AF=AD+DF=AD+DE= AD+DC.

但是，教学中发现，受等腰三角形三线合一的惯性思维影响，过顶点向底边作垂线，构成三线合一基本图形，如果没有发现AC可作为某个角平分线而进一步翻折的意识，是很难完成证明的.由于本题顶角的特殊性，在AD的延长线上补上DF=CD后，正好可以进一步补成含30°的直角三角形，从而利用角平分线AD的对称性翻折构造，与三线合一对接，实现各线段的关系转化，从而突破思维僵局.正是基于“等角共边可翻折”的构图补形经验，所以不会考虑把AD移到CD的延长线或其反向延长线上去补短.

图4

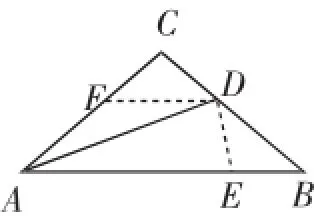
图5

证法4：平行线+角平分线构等腰：通过证法2利用三线合一的通法可行性的探讨，当角平分线遇上平行线时，可构等腰三角形，即在角平分线上取一点，过这点向该角的一边作平行线，构建等腰三角形，这也是一种常规思路，对于本题是否可行？

证明：如图5，取AE=AD，过D作DF∥AB交AC于F.由∠C=100°，BC=AC，易得∠CAB=∠B=40°.由DF∥AB，得∠FDA=∠DAB.因为AD平分∠CAB，所以∠CAD=∠DAB，从而∠CAD=∠FDA，于是FD=FA.

由DF∥AB，得∠B=∠CDF=40°，∠CAB=∠CFD= 40°.由AC=BC，得∠CAB=∠B，所以∠CFD=∠CDF，从而有CF=CD，所以AC-CF=BC-CD，于是AF=BD，从而FD= BD.由AD=AE，得∠ADE=∠AED.由AD平分∠CAE且∠CAE=40°，得∠DEA=80°，所以∠DEB=100°.在△CFD和△EBD中，∠CFD=∠BDE，FD=BD，∠CDF=∠B，则△CFD≌△EDB，所以CD=BE，从而AB=AE+EB=AD+CD.

证法4显然简洁，而且再次验证了平时积累的证法经验是可借鉴的，课堂中有意识提炼这种类似的基本模型图也是有必要的，于是有学生有了新的思考.能否利用角平分线向角的两边作垂线，用这种基本模型去获得解题思路呢？

证法5：“角平分线+双垂线”构全等转化：由于角平分线所在直线是角的对称轴，向角的两边作垂线可视作图形翻折，其实就是角平分线定理，再进一步发现，连接两个垂足也容易得到等腰三角形，因此，课堂教学中理应把这个图形提炼成一个基本的几何图形.

证明：如图6，过D作DE⊥AC于E，DF⊥AB于F，取FG=CE.

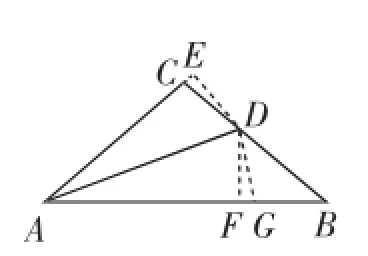
图6

由角平分线定理易得DE=DF.

在Rt△CED和Rt△GFD中，DE= DF，CE=FG，可证Rt△CED≌Rt△GFD，则CD=DG，∠DGF=∠ECD.

由∠C=100°，得∠ECD=∠DGF=80°.由AC=BC，得∠CAD=∠B=40°.又∠DGF=∠B+∠BDG，所以∠BDG=∠B=40°，从而DG=GB，于是DC=DG=BG.

由AD平分∠CAD，得∠DAB=20°.又∠DGB=80°，由三角形内角和定理得∠ADG=80°，从而∠ADG=∠AGD，所以AD=AG.从而AB=AG+GB=AD+CD.

三、变式分析

解后，有学生提问，如果在不改变条件的情况下，改变顶角的度数，又有哪些线段之间有数量关系？或者，弱化或强化条件，原题中角平分线改为腰上的中线，又会得出哪些结论？带着这些思考，笔者查阅资料，通过递进式变式设问，改变问题背景，与学生一起进行进一步探索.

变式1：如图1，三角形ABC中，CA=CB，若∠C=108°，AD平分∠A交AC于D，探究：AB等于哪两条线段长的和呢？试证明.

变式1中只改变顶角度数，由角平分线AD，可模仿翻折去截长，即在AB上取AE=AC，易得CD=DE，从而有AB=AC+BD.在巩固截长补短探求线段和差的方法时，发现成等量关系的线段发生了变化，那么，这些线段之间的关系是不是与顶角的度数有着某种联系？是不是只有当顶角为某一特定值时，才存在这种线段的数量关系？

在图2中，我们借助设元，利用方程思想进行探究.设∠C=β，则∠B=90°-，∠DEA=β，当β=60°时，翻折时发现C与B重合，当β＜60°时，翻折后E落在AB的延长线上，此时∠DBE=90°+β，此时线段之间的等量关系，只有当∠BDE=∠E=β时才可能存在，从而90°-=β+β，求得β=36°，即当∠C=36°时，有AC=AB+BD.用同样方法可发现：

通过探讨，发现等腰三角形中只有顶角为某一特殊角度值时，底角平分线及分一条腰所得的线段、底边、腰等之间才可能存在一种数量关系，从而可以抓住图形本质，特别是顶角为100°时是最为典型的习题，在多样化的解答中可以提升能力.那么，如果变等腰为非等腰，保留角平分线，在顶角为100°时，增补什么样的条件，可作类似的探讨？

变式2：如图7，已知△ABC中，∠A=100°，∠ABC= 30°，BD平分∠ABC交AC于D，求证：AB+AD=BC.

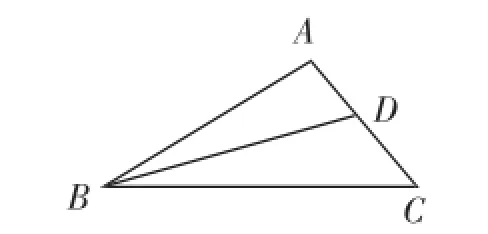
图7

变式2继续沿角平分线翻折而截长，可在BC上取一点E，使BE=AB，证△ABD≌△EBD，再利用三角形内角和定理，导出∠EDC=∠ECD=50°，得出DE=EC，所以BC= BE+EC=AB+DE=AB+AD.

通过研究，这类线段和差问题，图形必定要满足特殊条件，因而，解答时，抓住特殊条件分析，定会获得思路.

如果特殊到是等腰直角三角形，再增补或弱化条件，例如过底边另一端点作一条底角平分线的垂线（变式3），或者过直角顶点作一条腰上的中线的垂线（变式4），一定会存在某些数量关系，而在解决时，截长补短的转化策略再次得到提升，而且在解答中，会收获更多的方法和经验，各种不同方法可以运用不同的知识源.读者若有兴趣，不妨试一试.

变式3：如图8，AB=AC，∠BAC=90°，BD平分∠ABC，CE⊥BD交BD的延长线于E，求证BD=2CE.

图8

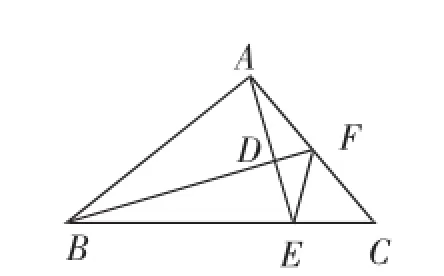
图9

变式4：如图9，AB=AC，∠BAC=90°，点F是AC的中点，过A作AD垂直BF，垂足为D，延长AD交BC于E，连接EF，求证：AE+EF=BF.

四、三点思考

解题有道，解题之道源于自然，解题之法源于几何图形的位置和性质.准确利用条件，调取大脑中存储的图形、知识、方法等模块，从而获得自然的解法.尊重自然、敬畏自然，适度改造自然、美化自然，这是人类生存的不舍追求.解题理应如此，寻找通性通法，然而，解题思路受阻也正常存在.因此，想方设法引导帮助学生主动切换思维视角，化隐为显、化难为易，实现解题从自然到完美的蜕变和升华，理应是教师解题教学坚守的目标.利用几何图形的位置与性质，适度提炼，合情转化，适度变式，可以帮助学生积累解答经验，大胆构图，展开联想，开启解答思路.

1.联想基本方法，合情转化，可以摆脱解题困境

从上述解法中不难看出，解法多样化源于思维视角多层次切换，把数学知识转化为解决问题的能力.解决本题的思考方向，就是截长补短，由此调取与之相关的知识源，回顾线段和差，角平分线定义与性质，等边对等角，三线合一，三角形内角和定理及三角形全等相关的几何概念与性质，结合题目条件，合情转化，启迪思路，摆脱解题困境.

如证法2中，在三线合一的惯性思路下，作底边上的高后，如果没有坚实的基础知识（30°角所对的直角边等于斜边的一半），不主动捕捉题中∠ADB=120°，主动切换思路，将直接影响解答.研究解法，并不是炫解题技巧，而是立足常规思路，思考如何借助知识源，合情转化，打开思维，联想思构，回联基本图形.

2.积累基本图形，合理提炼，可以助推解题智慧

初中阶段主要涉及的全等变换有平移，轴对称，旋转.而本题中的各种解法，正是基于角平分线是角的对称轴，借助轴对称变换.教学时，有意识引导学生，将角平分线与平行线和垂线进行组合，提炼出角平分线+平行线，角平分线+垂线两种基本图形，花一点时间，研讨这类基本图形的位置与性质，从而增强解题智慧.这种提炼是合理的，是“模式识别”策略具体落实在解题教学中.但是，模式化解答不等同于模型思想，绝不能把简单的几何基本图形，与模型思想混为一体.所提炼的基本图型，只是丰富学生视野，开阔学生思维，为解答提供可迁移和合理联想的参考方向，因而，提炼基本图形并不是加重学生负担，它仅仅是丰富了学生对图形的直观认识，或者只是一个图形模式，这种图形模式化解答绝对不是模型化思想，最多只是一种基本套路（如等角共边可翻折等）.如证法1中截长法是比较自然的思路，抓住了角平分线是角的对称轴这一图形的结构特征.

3.提升基本能力，适度变式，可以丰富解题经验

教学中，适度的变式是必要的，可以帮助学生掌握一类题的共性解法，在变式中丰富学生的解题经验，在变式中形成能力，在变式中可以生长.由于原题中图形的特殊性，可以有文中列举的多种解法，研究解法，是让学生掌握其中最适用的通性解法，加以变式练习，弱化模式，强化方法，洞察图形深层结构，矫正模式化伪解题能力的偏差，优化思维水平.如原题中，回溯基本知识，展开联想，或作双角平分线，或辅助图，或补正三角形等角度思考，突破思路障碍.

精致的变式不等同于题海，模式化解答无法与模型思想相提并论.然而，过度的变式会形成一种可套用的基本模式，让学生形成一种解题能力的条件反射.变式教学要适度，坚持以知识转化为思路引领，坚持以怎样做，怎么想到这样做，同一类型还可怎么做的三步曲，并且有意识融合教学逻辑与学生认知逻辑，以学生为中心，以能力为本，将数学建模作为教学的过程与手段而构建与运用数学模型，避免出现无模式可套就束手无策的困境.

1.姜晓翔.探寻自然解法，揭示问题本质［J］.中学数学教学参考（中），2015（7）.

2.李海燕.专题突破再反思，变式改编为研讨——以2015年江苏镇江第28题为例［J］.中学数学（下），2015（9）.

3.刘华为.浅谈基于知识转化下的专题复习——以图形面积一线三等分问题为例［J］.中学数学（下），2015（8）.

4.李景财.一道几何题解法的自然生成［J］.中学数学教学参考（中），2015（10）.

5.钱德春.初中数学“模型”教学之我见［J］.中学数学（下），2016（5）.Z