数学建模显捷径，一题多解求面积———巧用模型求抛物线中的三角形面积

☉湖北省丹江口市均县镇初级中学 周善宏

数学建模显捷径，一题多解求面积
———巧用模型求抛物线中的三角形面积

☉湖北省丹江口市均县镇初级中学 周善宏

【问题】已知平面直角坐标系中△ADE三个顶点的坐标（E在AD下方），求△ADE的面积.

图1

图2

图3

【建模】

如图1，过点E作EF∥y轴，交AD于F；作AH⊥EF于H、DG⊥EF于G.

则S△AED=S△AEF+S△DEF=×EF×AH+×EF×DG=×

如图2，过点A作AF∥x轴，交DE于F；作EH⊥AF于H、DG⊥AF于G.

则S△AED=S△AEF+S△ADF=×AF×EH+×AF×DG=× AF×（EH+DG）=×AF×|yD-yE|.

如图3，过点E作EF⊥AD于F.则S△AED=×AD×EF.

【应用】

例抛物线y=ax2-2ax-4与x轴交于点A、B（A在B的左边），与y轴交于点C，直线y=kx+2k经过点A，交抛物线于第一象限内的D点，且D点的横坐标为5.（1）求抛物线及直线的解析式；（2）若E为AD下方抛物线上一点，当△AED的面积最大时，求点E的坐标.

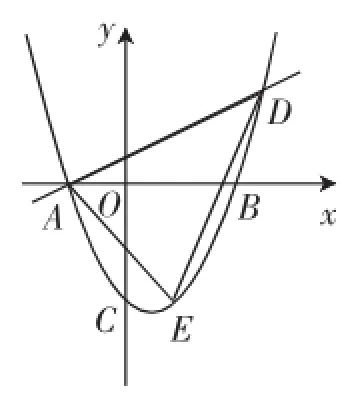
图4

解：（1）当y=kx+2k=0时，x=-2，则A（-2，0）.

由抛物线y=ax2-2ax-4与x轴交于点A，得a×（-2）2-2a×（-2）-4=0，解得

（2）【解法1】如图5，过点E作EF∥y轴，交AD于F.设E（x，y），其中-2＜x＜5.

图5

则

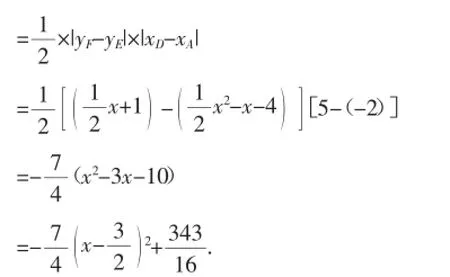
【解法2】如图6，设DE交x轴于F，其中-2＜m＜5.

图6

则

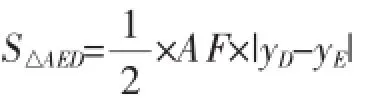
【解法三】如图7，作EF⊥AD于F，设过E点与AD平行的直线l的解析式为

图7

则S△AED=×AD×EF=·

当△AED的面积最大时，EF最大，此时直线l与抛物线只有一个交点.

当Δ=（-3）2-4（-8-2m）=0时，m=-，x1=x2=.