“分类讨论”：需要，但不能“失控”——以两道繁杂分类讨论考题为例

☉江苏省如皋市搬经镇高明学校 黄志峰

“分类讨论”：需要，但不能“失控”
——以两道繁杂分类讨论考题为例

☉江苏省如皋市搬经镇高明学校 黄志峰

每年上半年是中考复习的关键时期，这段时间学生会经历多次的模考练习，然而有些模考试题由于随意复制、粘贴，简单的拿来主义，为了在最后一题追求所谓的压轴题，为了难住优秀学生，往往容易选取一些需要分类讨论的考题，但也有一些考题由于命题者个性化喜好，考题的分类讨论陷入失控、无度的范围，使得备考师生茫然无措，本文列举两道模考题，并跟进批判与商榷，提供研讨.

一、两道繁杂分类讨论的模考题

考题1（2014年浙江湖州中考卷）如图1，已知在平面直角坐标系xOy中，O是坐标原点，以P（1，1）为圆心的⊙P与x轴、y轴分别相切于点M和N，点F从点M出发，沿x轴正方向以每秒1个单位长度的速度运动，连接PF，过点P作PE⊥PF交y轴于点E，设点F运动的时间是t秒（t＞0）.

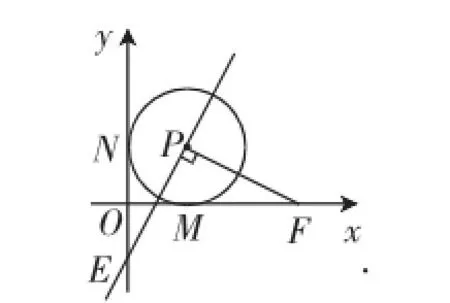
图1

（1）略；

（2）在点F运动的过程中，设OE=m，OF=n，试用含m的代数式表示n；

（3）作点F关于点M的对称点G，经过M、E和G三点的抛物线的对称轴交x轴于点Q，连接QE.在点F运动的过程中，是否存在某一时刻t，使得以Q、O、E为顶点的三角形与以P、M、F为顶点的三角形相似？

思路概述：限于篇幅，我们不准备详细讲评思路突破，只是简略提及该题的分类讨论的要点.

（2）所配图形只是示意图，需分别思考点E在y轴负半轴或正半轴或原点时的情况.

（3）需要分很多种情况讨论，一级分类可以从1＜t＜2，t＞2开展，然后二级分类再从不同的三角形相似对应边的情况进行考虑，列出相应的比例式构造方程求解，求解关键是用含t的式子表示点Q的坐标及OQ的长.

考题2（2014年吉林长春中考卷）如图2，在矩形ABCD中，AB=4，BC=3，O为对角线BD的中点，点P从点A出发，沿折线AD-DO-OC以每秒一个单位长度的速度向终点C运动，当点P与点A不重合时，过点P作PQ⊥AB于点Q，以PQ为边向右作正方形PQMN，设正方形PQMN与△ABD重叠部分的面积为S（平方单位），点P运动的时间为t（秒）.

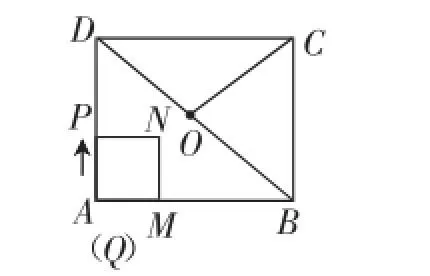
图2

（1）求点N落在BD上时t的值；

（2）直接写出点O在正方形PQMN内部时t的取值范围；

（3）当点P在折线AO-DO上运动时，求S与t之间的函数关系式；

（4）直接写出直线DN平分△BCD的面积时t的值.

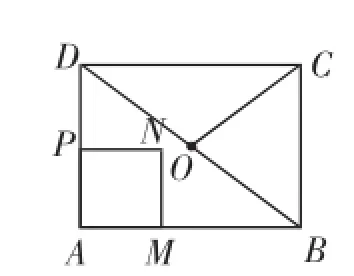
图3

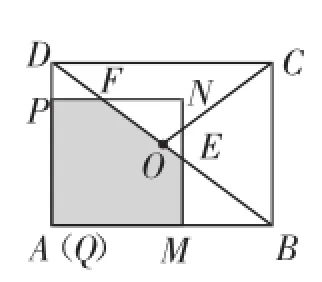
图4

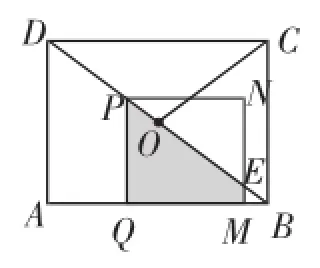
图5

思路概述：这道考题以运动变化为背景，在点P沿折线运动时，伴随一个正方形的变化而增加解题层次，从第（2）问就需要考虑不同的运动位置，数学直觉的理解要求渐高.而第（3）问则需要分当0＜t≤＜t≤3，3＜时，对应着图3、图4、图5的三种情况.最后一种情况运算量渐大，待求S即为梯形PQME的面积，即S=S梯

第（4）问首先要想清点N落在△BCD的中线DE上.然后再分不同情形构造图形，当点P在线段AD上（如图6）；当点P在线段DO上（如图7）；当点P在线段OC上（如图8）.

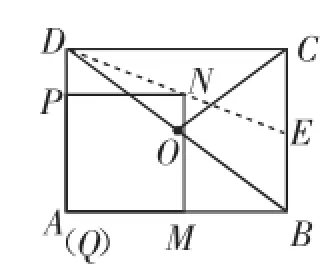
图6

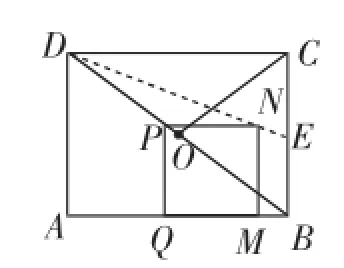
图7

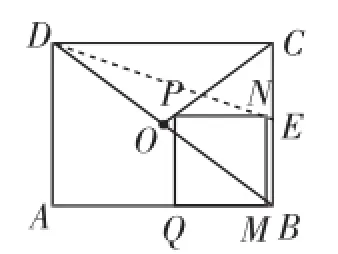
图8

值得一说的是，如果检索网络上传播的该题答案，笔者下载后以5号字打印规范过程，使用了5页A4纸，实在让人惊讶！这样的冗长解答的试题是怎样通过层层打磨、审题，最后成为一道中考试题，而且又在各级模考试题中频繁出现的？难道这种流行题型代表了当前的一种压轴题命题方向？以下就围绕全卷命题时对分类讨论的考查展开一些反思.

二、全卷命题时“分类讨论”考查的思考

1.分类讨论是重要的数学思想方法，全卷命题时需要考查

进入初中之后，数系进一步扩充，欧氏几何上场，很多数学概念都存在多种表现形式和可能的情况，这时分类讨论的解题方法就频繁登场，从初一到初三各级考试中，几乎每份试卷都会涉及分类讨论的考查，这是值得肯定的.具体来说，有理数引入之后，用一个字母a表示一个数时，就需要引导学生分类思考数a是正数、零、负数；将其对应在数轴上的点A，就需要引导考虑点A与原点的位置关系，而这些都是后续平面直角坐标系、函数图像问题研究的基础.根据教学经验，学生在中考时一道综合题中没有分类讨论，深究起来，往往由他在初一时对一个点与原点位置关系的分类理解不深导致.这也就要求我们在初中起始阶段只要有分类讨论的必要，就要在全卷设计时进行考查和关注，以使让学生重视分类讨论的思想方法.

2.分类讨论考查学生思维的缜密性，全卷不宜多次考查

分类讨论思想方法主要考查学生思维的缜密性，不重不漏地思考所有情况，不但是教学中要重视的训练方向，同时在全卷命题时也要充分考虑.但是全卷考查要求覆盖知识点的全面性，考查数学思想方法的多样化，包括数形结合、数学建模、分类讨论、待定系数、整体思想、抽象分离、排除干扰等数学能力都在考查范围，可以根据全卷考查范围而有所侧重，但不可偏废，特别是在全卷30道小题的考查中，出现4道或以上考题都需要分类讨论，这就值得商榷了.事实上，从测量学角度上说，如果学生在思维缜密性上偏弱时，全卷考查时多次考查这个维度，造成该考生反复失分，对该考生也是一种反复“伤害”，这是值得命题时注意的.

3.分类讨论考查数学核心概念理解，注意适当切忌“失控”

如上所述有理数范围的分类讨论那样，关注数学核心概念的理解是全卷考查的重点，除了代数领域有很多分类讨论的案例，在几何学中也有很多这样的案例.比如图形位置关系的领域中，以初一所学的点和直线位置关系来说，分两种：点在直线上、点在直线外；初三所学的点与圆的不同位置关系、直线与圆的位置关系、圆与圆的位置关系等，都是“一脉相承”的，属于同一类型的研究套路，全卷命题时要注意兼顾这些数学概念的考查，考查学生分类讨论的掌握情况.但是像上面模考1就陷入了失控的状态，即分类讨论无需累加到如此地步，要知道对于当下“时间紧、题量大”的考试来说，如果平心而论，也许120分钟的考试，只要一道“模考1”就够学生忙得不亦乐乎了；再比如模考2这道考题，从第（2）问就开始要考虑运动的两处极端位置，到第（3）、（4）问的分类讨论已陷入“失控”状态，对于优秀考生来说，思路一看就知，但是构造图形、繁杂运算之路漫漫，这种导向“少思多算”的命题风格也许就是命题组的数学旨趣和教学取向.作为重要影响的考试来说，以这样的数学试卷传递一个地区的命题导向，“逼着”全样本的学生思考命题组个人喜欢的数学问题，实在让人遗憾.

三、命题改编

知易行难，以下本着个人兴趣，对模考题2给出笔者的变式改编，提供分享.

考题2变式改编如图2，O为矩形ABCD的对称中心，AB=8cm，BC=6cm.点P从点A出发，沿折线AD-DOOC以2cm/s的速度向终点C运动，过点P作PQ⊥AB于点Q，以PQ为边向右作正方形PQMN.设运动时为ts.

（1）当t=2时，点N是否落在BO上吗？为什么？

（2）直接写出中心O在正方形PQMN内部时t的取值范围；

（3）当直线DN平分△DOC的面积时，求t的值.

改编意图：删减了原题的第（2）问，精减了题干表述，而且第（3）问需要学生组织语句，增强解答题的过程要求.

四、写在最后

命题研究是一个非常广泛的教研领域，不但涉及具体试题的呈现形式、难易把握、考查侧重点的预设和研磨之外，将一道试题放到整卷中某一个位置时，仍然需要思考该题在全卷中的地位、价值、导向，特别是该题与全卷中其他试题之间的相容性，都是需要精心构思的.从这个角度看，当下很多简单拼凑的试卷还不在少数，个别地区的命题还采用所谓的网络自动组卷来应对，想来，在命题如此专业化的领域，智能化时代似乎来得太早了吧？

1.刘东升.一次期中考试阅卷随笔［J］.中学数学教学参考（中），2016（1-2）.

2.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

3.夏德祥.繁简难易：中考把关题的命题研讨——以2016年江苏扬州中考第28题为例［J］.中学数学（下），2016（7）.

4.杨卫东.客从何处来：一道几何把关题的命题历程［J］.中学数学（下），2016（8）.

5.朱国生.反思考题难点，预设“一题一课”——以2016年江苏南通中考卷第28题为例［J］.中学数学（下），2016（9）.H