经典问题有新意，命题教学双引领——由清华附中初三上学期月考压轴题说起

☉江苏省扬州市邗江实验学校 刘黎铭

经典问题有新意，命题教学双引领
——由清华附中初三上学期月考压轴题说起

☉江苏省扬州市邗江实验学校 刘黎铭

在当下月考制度是很多学校一项教学常规之时，不少月考卷的质量低下也常常成为人们评论的热点，而在一些重点学校往往比较重视校级层面的命题与审题工作，而且能有一两道把关题精心设计，推陈出新，既有效检测了学生近期学习的效果，又引导着数学知识的前后关联.本文关注一道北京清华附中初三月考题，先给出解题思路，再跟进命题和教学思考，提供研讨.

一、考题及思路突破

考题（2016～2017学年北京清华附中初三12月份月考卷）如图1，在正方形ABCD中，P是边BC上的一个动点（不与B、C重合），线段AP的垂直平分线分别交AB，DC于M，N两点，AP交MN于E点.

（1）求证：MN=AP；

（2）如图2，连接DB，交MN于点Q，求证：EQ=ME+NQ.

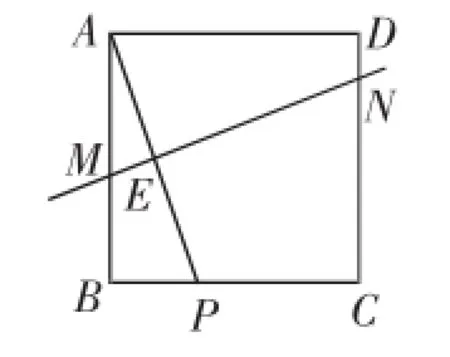
图1

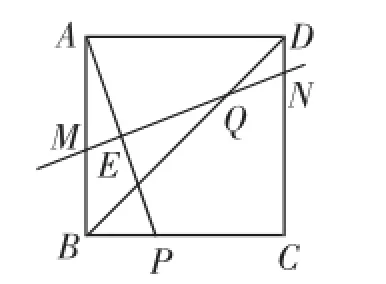
图2

思路简述：（1）这是关于正方形的一类经典问题，在图1中，AP⊥MN时，一定能证出AP=MN.构造全等三角形可实现证明，具体说，有如下两种构造全等的方法，如图3、图4.

图3

图4

在图3中，证明△ABP≌△DAG，可得DG=MN=AP；在图4中，证明△ABP≌NGM，MN=AP.

（2）这个待证的结论比较奇异，要实现证明需要较强的几何构造能力.切入点是利用正方形的轴对称性质、线段垂直平分线性质，以及上一问的结论MN=AP.

构造图5，容易发现本题的深层结构，根据正方形的轴对称性质有QA=QC，根据MN垂直平分AP，有QA=QP，容易发现A，P，C三点均在圆Q上，此时结合同弧所对的圆周角是圆心角2倍，有∠AQP=2∠ACB=90°，所以△APQ是等腰直角三角形.而QE⊥AP，根据三线合一，有QE=AP，等量代换得QE=MN.即EQ=ME+QN.

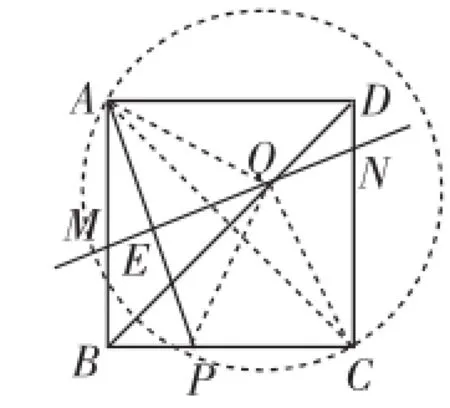
图5

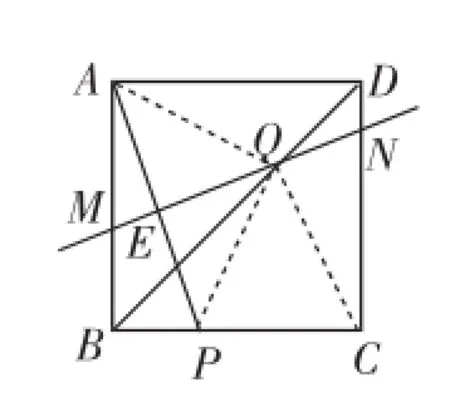
图6

解后反思：第（1）问比较经典和简单，这里不再给出说明.第（2）问在上述证明过程中一个重要进展是证出“△APQ是等腰直角三角形”，有了这个进展，可以利用直角三角形斜边上的中线沟通QE=AP.以下我们再从另外的角度贯通思路：

另解1：从上面的分析知，问题的关键是证∠AQP为直角.如图6，根据对称性有AQ=CQ，由线段MN垂直平分AP，所以AQ=PQ，所以∠BAQ=∠BCQ=∠QPC，所以∠BAQ+∠BPQ=180°，所以在四边形ABPQ中，∠AQP+∠ABP=180°，所以∠AQP=90°，于是问题获得突破.

图7

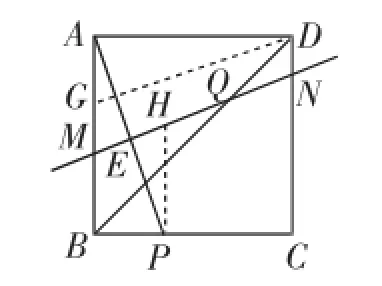
图8

另解2：根据对称性可考虑作QG⊥AB，QH⊥BC，垂足分别为G，H，再证△AQG≌△PQH，可得∠AQP=∠GQH=90°，问题获得突破.

另解3：（截长补短，问题转化为证明两条线段相等）如图7，作PH⊥BC交MN于H点，易证△AME≌△PHE，HE=ME，PH=AM.接着平移线段MN至DG，易证△DAG≌△ABP，AG=BP=PK，HK=MG=DN.

接着证出HK=DN，HK//DN，△HKQ≌△NDQ，HQ= NQ.所以ME=EH，HQ=NQ，EQ=ME+NQ.

二、命题思考

1.经典问题，推陈出新，简约呈现，引发深思

清华附中初三月考卷选用一道八年级经典正方形问题作为设问背景，推陈出新，题干简约好懂，呈现简约，图形线条也不是很多，第（1）问比较基础，引导更多学生参与进来，但是要想解决第（2）问又需要有足够的挑战实力，对正方形轴对称性质、线段垂直平分线的性质有较为充分的考查.

2.指令明确，殊途同归，蕴藏结构，值得回味

在本考题简洁呈现之外，我们还注意到问题设问上指令明确，最后一问直截了当，让学生证明，而不是猜想三条线段之间的数量关系.具体求解时，可以走“截长补短”的全等路径，但构造较繁，而基于“共圆”的视角可洞察问题的深层结构，使得考题求解之后，仍然有深入思考的空间，值得回味.

三、教学思考

1.重视对经典问题的再回顾，洞察问题结构

这道试题给我们带来了很多教学启示，比如，要重视对经典问题的再回顾，以几何为例，初中几何经典问题是很多的，这些几何问题在七年级、八年级、九年级都会出现，解决的角度或层次都不一样，学生获得的理解方法也不一样.比如七年级几何初步时，可以安排学生度量四边形的四边之和与对角线之和的大小，并运用尺规作图验证性质；而到八年级三角形一章时，可以利用三边之关系证明；再比如在八年级上学期三角形学习时，涉及两边中点连线段（中位线），可以通过度量、验证出三角形中位线与第三边的位置和数量关系，而到八年级下学期学习平行四边形之后，可以探究三角形中位线性质，而且可以提出一个重要的命题“求证三角形一边上的中线与另外边中点连线段互相平分”，这样就可关联八年级上册、下册的学习内容.而像上文中的考题这样，可以引导学生站在初三圆的高观点反观之前所学、所证的习题与思路，洞察问题的深层结构，对问题的理解达到新的高度.

2.重视对精准作图的严要求，加强文图对应

笔者曾有机会研习上个世纪我国著名数学教育家傅种孙先生编写的《平面几何教本》，该教材中傅先生十分重视几何作图的示范与纠错.根据我们的教学实践，目前的几何教材中对作图的要求一降再降，各级考试中对作图的要求也一降再降，这不得不说是一种遗憾.我们发现，不少学生的几何能力偏弱，常常表现在阅读几何语言、符号语言时，不能精准对应到图形上去，有些学生甚至根据几何语句不能唯一对应地画出精准图形，从而思路受阻.从这意义上说，清华附中这道考题第（2）问求证时，需要学生其有较为精准的构图能力，也是对教学的一次强有力的引领.

3.重视考后讲评与反思分析，开展变式再练

平时的阶段测试之后，除了要针对学生得分情况进行应试层面的分析，还需要精心构思试卷中典型问题的讲评与变式拓展，比如引导学生分析不同解法之间的关联，不同解法繁简的对比，不同解法对应着哪一个年级哪个章节中的某个数学知识或性质，一种解法的念头是如何产生的，怎样回归到基本概念获得思路突破等，多引导学生反思回顾，有不少老师安排学生以“数学写作”的方式究错或订正，也是一种值得提倡的方式.作为文末，我们也对上文中的考题做出变式改编，提供分享：

变式再练题：如图1，在正方形ABCD中，P是边BC上的一个动点（不与B、C重合），线段AP的垂直平分线分别交AB，DC于M，N两点，AP交MN于E点.

（1）当P为BC边的中点时，求tan∠AMN的值.

（2）在（1）的条件下，试比较AE与BP的大小，并说明理由.

（3）如图2，连接DB，交MN于点Q，连接AQ，PQ.

①判断AQ与PQ的位置关系，并说明理由；

②求证：EQ=AE；

③当点Q为△APM的外心时，求tan∠MQB的值.

改编意图：前两问属于特例引路，并且引导学生回顾正切函数的定义，与最后一问的正切函数值做好呼应；第（3）问对应着原考题的第（2）问，但增加“判断AQ与PQ的位置关系”是个台阶，学生探究出它们之间垂直关系之后，可以发现△AQP是等腰直角三角形，对于进一步研究“EQ=AE”是有益的；而最后一小问是圆Q的一种特殊情况，即该圆与AB边的另一个交点恰为M点，此时∠AQM=∠MQP=∠PQC=45°.

1.张英伯.傅种孙——中国现代数学教育的先驱［J］.数学教育学报，2008（1）.

2.傅种孙.平面几何教本［M］.北京：北京师范大学出版社，1982.

3.鲍建生，顾泠沅，等.变式教学研究［J］.数学教学，2003（1，2，3）.

4.许燕.从解题赏析走向教学研究——以2016年无锡卷第27题为例［J］.中学数学（下），2016（10）.H