大规模图数据的k2-MDD表示方法与操作研究

董荣胜 张新凯 刘华东 古天龙

(广西可信软件重点实验室(桂林电子科技大学) 广西桂林 541004)(ccrsdong@guet.edu.cn)



大规模图数据的k2-MDD表示方法与操作研究

董荣胜 张新凯 刘华东 古天龙

(广西可信软件重点实验室(桂林电子科技大学) 广西桂林 541004)(ccrsdong@guet.edu.cn)

对包含亿万个顶点和边的图数据进行高效、紧凑的表示和操作是大规模图数据分析处理的基础.针对该问题提出了基于决策图的大规模图数据的一种表示方法——k2-MDD，给出了k2-MDD的构造过程以及图的边查询、外(内)邻查询、出(入)度查询、添加(删除)边等基本操作.该表示方法在k2树的基础上进行优化与改进，对图的邻接矩阵进行k2划分后，采用多值决策图进行存储，从而达到存储结构更为紧凑的目的.通过对来自米兰大学LAW实验室的一系列真实网页图和社交网络图数据的实验结果可以看出，k2-MDD结构在节点数上仅为k2树的2.59%～4.51%，达到了预期效果.通过对随机图的实验结果可以看出，k2-MDD结构不仅适用于稀疏图，同样也适用于稠密图.图数据的k2-MDD表示，既具有k2树表示的紧凑型和查询的高效性，又能实现符号决策图表示下图模式的高效操作，从而实现了描述和计算能力的统一.

图数据；存储优化；k2-MDD；k2树；决策图

随着移动互联网、物联网等技术的发展，众多新应用以前所未有的方式和速度产生并积累着大量数据.在众多类型的大数据中，图数据作为一种有效描述大数据的数据结构，扮演着越来越重要的角色[1-2].由于图数据的规模日益庞大，如何对图数据进行高效的存储以及如何对图数据进行高效的操作是当前面临的两大挑战.以社交网络为例，根据GlobalWebIndex统计，Facebook用户量已经超过11亿，平均每个人的好友超过100位，使用邻接表来存储所有用户的关系信息，需要接近1TB的存储空间[3]；以互联网为例，根据中国互联网络信息中心(CNNIC)发布的《第37次中国互联网络发展状况统计报告》[4]，截至2015年12月中国网页数量为2 123亿个，超链接数量据估计超过1013，使用邻接表来存储网页直接的链接关系信息需要超过16 TB的存储空间.同时随着用户量和信息量的快速增长，问题也只会变得越来越严峻.

为了对图数据进行紧凑表示，在传统的邻接矩阵表示法的基础上，Brisaboa等人[5]于2009年提出了基于k2树(k2-tree)的方法，树中的每一层对应于邻接矩阵或分块子矩阵的分块子矩阵，节点对应于邻接矩阵的分块子矩阵，生成的k2树使用2个位向量T和L来存储，该方法不仅能够紧凑表示邻接矩阵，而且能实现邻接节点的正向或逆向高效查询操作[6].施佺等人[7-8]给出了k2树表示方法的2种优化技术：启发式深度优先节点重排序和自适应修正k，使得所表示的结构更为紧凑，节点得到明显的减少.

但是，不论是k2树还是施佺等人优化过的k2树，在对大规模图数据表示时仍具有一定的局限性，具体表现在3个方面：

1) 当图的规模变大时，图内部本身就会存在大量的同构子图.同样地，当按照k2树的思想把邻接矩阵进行划分后，也存在大量的相同的子矩阵.这就造成了k2树内也存在大量的同构子树.

2)k2树仅对稀疏图有效，当图变的稠密时，由于邻接矩阵内可被压缩的0节点变少，因此k2树紧凑性也会变低.

3)k2树未涉及动态图(需要添加或删除顶点、边以及子图等的图)的表示与操作[5].

因此，k2树对上述图的结构特性尚缺乏必要的考虑，其在紧凑性上仍有较大的改善空间.针对k2树目前存在的问题，有必要对其进行进一步的优化与改进，以得到一种更为紧凑并且适用面更广的图数据的表示方法.为此，本文提出一种基于决策图的大规模图数据的表示方法——k2-MDD，该表示方法采用k2树的思想对邻接矩阵进行划分，然后使用多值决策图进行存储，使k2树中大量的同构子树所造成的冗余节点得到合并，从而达到存储结构更为紧凑的目的.该k2-MDD的优点主要有4点：

1) 由于采用决策图结构来存储图数据，因此对于划分邻接矩阵时产生相同的子矩阵，即k2树中的同构子树就自然地被合并了，最终生成的k2-MDD结构将比k2树紧凑得多.

2)k2-MDD与k2树所不同的是，它不论是0值还是1值，只要是同构的，都将被合并掉.因此，在表示稠密图时，k2-MDD节点数反而会变少，结构变得更为紧凑.

3) 当使用决策图来存储图数据后，图的相关基本操作就可以转化为符号决策图的逻辑操作，这就为动态图数据的高效操作提供了可能性.另外这也使得基于k2-MDD要比基于k2树的图的查询操作更为简洁.

4) 由于k2-MDD是基于决策图的结构，根据其本身结构的特性，该结构将更有利于子图查询、图同构、图子图匹配以及多图匹配等方向的研究.

本文以有向无权图为例，对k2-MDD的表示与操作进行讨论.本文提出的结构也可以拓展用于无向图以及加权图的存储与表示.下面给出k2-MDD的表示形式、定义、性质、构造过程以及对于有向图的基本操作等.

1 有向图的k2-MDD表示形式

首先给出k2-MDD的定义：

定义1.k2-MDD：图的邻接矩阵可以用一个将原始矩阵进行递归的k2等分后构造的多值决策图(multi-valued decision diagram, MDD)[9]结构来表示，这样的MDD称之为k2-MDD.

k2-MDD描述了一个带有n个变量的离散多值函数，f:D1×D2×…×Di×…×Dn→S，其中：

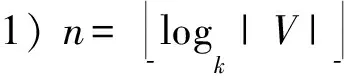
2)Di代表递归到第i层时对(子)矩阵的划分.Di={1,2,…,k2}为所有变量的有限值域，与每次对(子)矩阵划分得到的k2个子矩阵一一对应；S为多值函数f的有限值域，即k2-MDD终端节点的取值集合，其可能为布尔值(对应无权图)、有限整数集合或者有限实数集合(对应加权图).

3)k2-MDD的节点包括终端节点和非终端节点.

4) 非终端节点用xi表示，包含k2个指向其他节点的指针，这些指针和函数f对应，其形式化描述为

fxi=c=f(x1,x2,…,xi-1,c,xi+1,…,xn).

(1)

k2-MDD的图形化描述如图1所示：

Fig. 1 Graphical description of k2-MDD.图1 k2-MDD的图形化描述

Fig. 2 Reduction rules.图2 化简规则

从图1可以看出，给定多值变量x1到xn的一组取值，可以得到唯一的终端节点取值.

k2-MDD的化简规则与MDD相同，可以总结为3条：

规则1. 合并相同终端节点.同一属性的终端节点只保留一个，并删除其余相同属性的终端节点，原来指向这些已删除的终端节点的指针重定向到保留的终端节点上.

规则2. 合并相同内部节点.同一属性的内部节点(非终端节点)只保留一个，并删除其余相同属性的内部节点，原来指向这些已删除节点的指针重定向到保留的内部节点上.

规则3. 删除冗余节点.如果一个节点的所有指针都指向同一节点，那么该节点就是冗余节点，需将其删除，并将指向该节点的指针指向删除节点的孩子节点.

上述3条化简规则实例如图2所示，其中图2(a)表示多值函数f=xy，x的取值范围为x∈{1,2,3}，y的取值范围为y∈{1,2,3}，函数f的值域为集合{0,1,2}.

由k2-MDD的定义可以看出，图的邻接矩阵中任一单元均对应于n个变量的唯一一组取值，根据这组取值可以得到唯一函数值，即终端节点的值，并且该值与原始矩阵中对应单元格的元素值相等.

本文以无权图进行说明，因此函数f的值域取布尔值.对图中顶点数量等于k的若干次幂和图中顶点数量不等于k的若干次幂2种典型情况分别进行举例说明，其中k=2.

例1. 顶点数量等于k的若干次幂.

对于图3所示的有向图，其邻接矩阵如图4所示,k2树如图5所示.显然，图5中存在同构子树，如图6所示.

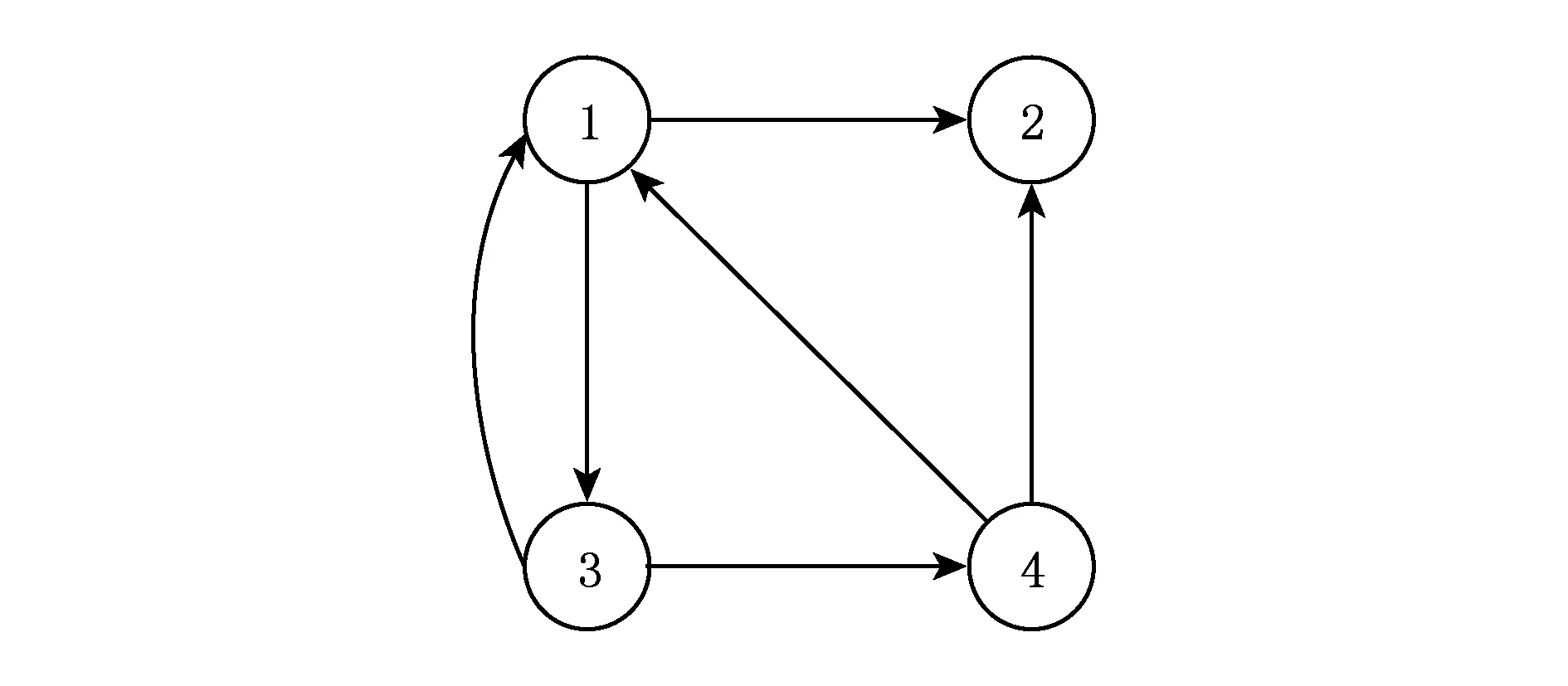
Fig. 3 Graph structure.图3 图结构

Fig. 4 Adjacency matrix of example 1.图4 例1的邻接矩阵

Fig. 8 k2 tree of example 2.图8 例2的k2树

Fig. 5 k2 tree of example 1.图5 例1的k2树

Fig. 6 Isomorphic subtrees in k2 tree of example 1.图6 例1的k2树中的同构子树

例2. 顶点数量不等于k的若干次幂.

当图中顶点数量不等于k的若干次幂时，可以通过增加邻接矩阵的行数和列数(新增的元素全都标记为0)来满足条件[3].如图7中的邻接矩阵，其原始图中有11个顶点，原始矩阵是11行乘11列的矩阵，通过增加5行5列0数据来使得矩阵可以被k2等分.从k2树原理及图8可以知道，这样增加全部为0的行列对最终生成的k2树产生的影响非常小.显然，图8的k2树也存在同构子树，图9标出了其中一部分.

Fig.7 Adjacency matrix of example 2.图7 例2的邻接矩阵

当图的规模变大时，k2树中相同的子树会变得越来越多，另外还有大量的0节点.这种现象在小规模图中也有体现，比如上述2个例子.

为了减少k2树中的节点数量，可以将k2树中的同构子树进行合并.而这正好是决策图[10]的优势.另外，这种合并的过程与MDD化简过程恰好吻合.对于无权图，使用布尔型MDD(终点要么是真要么是假)；对于加权图，使用整数或者实数型MDD(终点是整数或者实数).本文使用无权图进行说明，MDD中所有变量的有限值域均为{1,2,…,k2}.

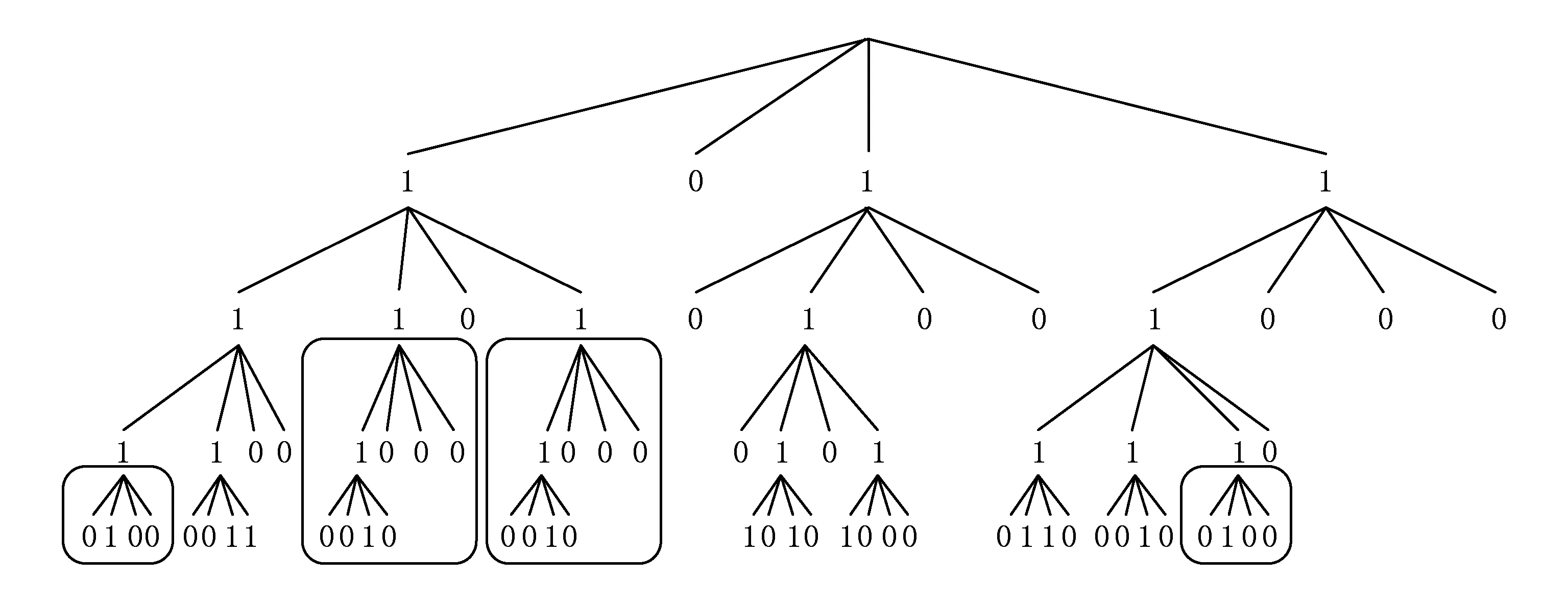
Fig. 9 Isomorphic subtrees in k2 tree of example 2.图9 例2的k2树中的同构子树

将上述2个例子的k2树转换为MDD后分别如图10和图11所示.图10、图11中节点内的数字仅代表该节点的索引号，并没有其他意义，图10、图11中左侧的数字为图中节点的层次序号.

从以上2例可以看出，从k2树转换为MDD后同构子树都被合并了，节点数量大大减少.例1从21个节点减少为6个节点，例2从73个节点减少为16个节点.

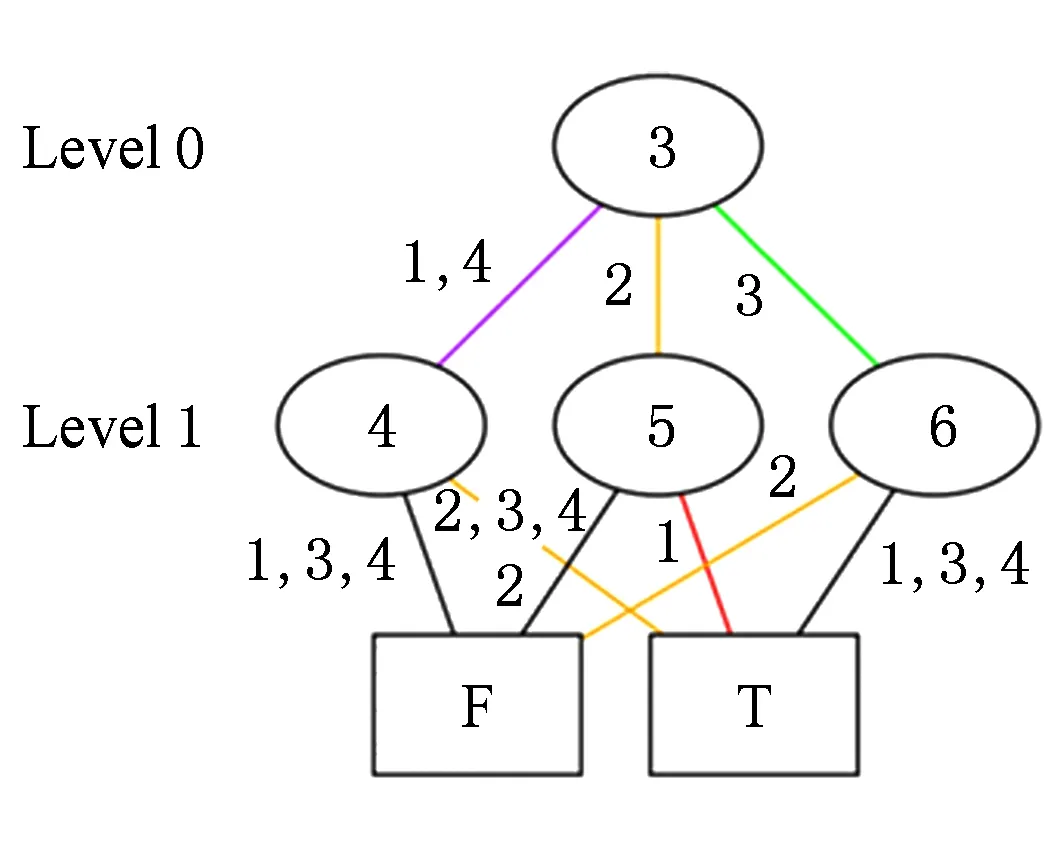
Fig. 10 The MDD of example 1.图10 例1的MDD

Fig. 11 The MDD of example 2.图11 例2的MDD

2 构造k2-MDD的算法过程

构造k2-MDD的过程分为对图的顶点进行编码、对边进行编码、根据边的编码来构造k2-MDD3个步骤，具体如下：

1) 对图的顶点编码

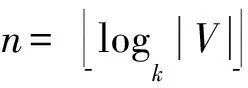
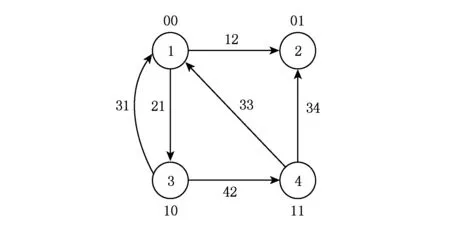
Fig. 12 Coding vertexs and coding edges.图12 顶点编码和边编码

算法1. 对图的顶点进行编码.

输入: 要进行编码的顶点的编号nodeID；

输出: 对应该顶点的编码数组nodeCode[].

①EncodingNode(nodeCode[],nodeID)*将编号为nodeID的顶点编码并存到数组nodeCode[]中*

②codeNum←CeilingLog_2(nodeNum);*codeNum为编码长度，nodeNum为顶点数量*

③low←1;

④high←Pow(2,codeNum);*取不小于nodeNum的2的若干次幂*

⑤i←1;

⑥ While (low≤high) Do*二分编码*

⑦mid←(low+high)2;

⑧ IfnodeID≤midThen

⑨nodeCode[i]←0;

⑩high←mid-1;

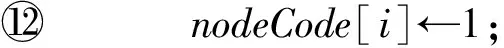
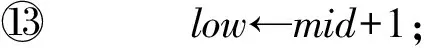
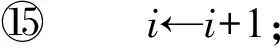
2) 对图的边编码

有向边可理解为顶点之间的关系，顶点v0到顶点v1的边可用特征函数E(v0,v1)来描述.当k=2时，设X=(x1,x2,…,xn),Y=(y1,y2,…,yn)是图中顶点的编码向量，则顶点X到顶点Y边的特征函数表示为

E(X,Y):{0,1}n×{0,1}n→{1,2,3,4}n,

即每一位上2个顶点的2种状态会组合出4种状态.因此，边的编码长度依然是n位，每一位是4种状态之一(1,2,3或4).边编码过程的伪代码如算法2所示.根据该编码规则对图3所示图的边编码后如图12所示.

算法2. 对图的边进行编码.

输入: 要进行编码的边的起止顶点编号nodeFrom和nodeTo；

输出: 对应该条边的编码数组edgeCode[].

①EncodingEdge(edgeCode[],nodeFrom,nodeTo)*根据边的起止顶点得到边的编码*

②EncodingNode(nodeCodeA[],nodeFrom)*对边的起始顶点进行编码*

③EncodingNode(nodeCodeB[],nodeTo)*对边的终止顶点进行编码*

④ Fori=1 TocodeNumDo*根据起止顶点的编码来对这条边进行编码*

⑤edgeCode[i]←nodeCodeA[i]×2+nodeCodeB[i]+1;

⑥ EndFor

3) 根据边编码的集合来构造k2-MDD

根据k2-MDD的定义，我们可以构造一个含有n个变量的k2-MDD，然后令这n个变量的值等于边编码集合里的值时，函数值为T，否则为F.这样就得到了与有向图G对应的k2-MDD.例如，根据图12中的边编码，可以得到图的k2-MDD结构如图10所示.在构造k2-MDD时可以借助MEDDLY(multi-terminal and edge-valued decision diagram library)函数库[11].MEDDLY函数库是为操控MDD提供的一个CC++开源项目，由爱荷华州立大学在Linux平台下开发，其中提供了丰富的MDD构造以及操作的函数.例如：可以使用createVariablesBottomUp()函数来创建将要构造MDD的变量个数以及每个变量的取值范围；使用createEdge()函数来根据给定的一组或多组变量的值来生成一个MDD；使用apply()函数以及UNION运算符来将2个MDD进行合并.通过MEDDLY函数库，根据边编码我们可以很方便地生成有向图对应的k2-MDD.构造k2-MDD的伪代码如算法3所示.

算法3. 构造k2-MDD.

输入: 图的所有边；

输出: 与输入图对应的k2-MDD.

①CreateK2MDD()*根据边生成k2-MDD*

② Fori=1 TocodeNumDo*设置变量个数以及每个变量的值域*

③Bounds[i]←4;

④ EndFor

⑤createVariablesBottomUp(bounds[],codeNum);*创建变量*

⑥EncodingEdge(edgeCode[],nodeFrom[1],nodeTo[1]);*对第1条边进行编码*

⑦createEdge(edgeCode[],1,all);*根据第1条边的编码生成一个初始化MDD*

⑧ Fori=2 ToedgeNumDo

⑨EncodingEdge(edgeCode[],nodeFrom[i],nodeTo[i]);*对第i条边进行编码*

⑩createEdge(edgeCode[],1,rest);*根据第i条边编码生成MDD并存到rest*

3 基于k2-MDD的有向图的操作

下面给出在k2-MDD存储结构下有向图的一些基本操作.

1) 边查询

根据边的起止顶点v1和顶点v2的编号得到该条边的编号E(v1,v2)，在图的k2-MDD中检测E(v1,v2)的函数值.若值为T，则该边存在，否则不存在.MEDDLY库中提供的INTERSECTION运算符可以帮我们完成此操作.INTERSECTION用来求2个MDD的交运算.因此，我们只要将原图的k2-MDD与要查询的边生成的k2-MDD进行INTERSECTION运算，查看运算结果是否为空即可.边查询的伪代码如算法4所示.

算法4. 边查询算法.

输入: 要查询的边的起止顶点编号nodeFrom和nodeTo；

输出: 该边是否存在.

①edgeQuery(nodeFrom,nodeTo)*根据边的起止顶点查询图中是否存在该边*

②EncodingEdge(edgeCode[],nodeFrom,nodeTo);*对边进行编码*

③createEdge(edgeCode[],1,tmp);*生成这条边的MDD*

④apply(INTERSECTION,K2MDD,tmp,res);*进行交运算，结果存到res中*

⑤ Ifres.getNode()=0 Then*如果结果为空，则边不存在；否则存在*

⑥Print(不存在);

⑦ Else

⑧Print(存在);

⑨ EndIf

2) 外邻查询(包括求出度)

借助边查询，将要进行外邻查询的顶点赋值为v1，图中所有顶点依次赋值为v2，检测E(v1,v2)的函数值.若值为T，则当前v2是一个外邻点，否则不是.通过统计外邻点个数可以得到该顶点的出度.

3) 内邻查询(包括求入度)

查询方法与外邻查询类似，只不过要查询的点赋值为v2，图中所有顶点依次赋值为v1.

4) 增加边

根据要增加边的起止顶点v1和v2的编号得到该条边的编号E(v1,v2)，生成该条边的k2-MDD;然后与原图的k2-MDD进行UNION运算，即得到增加了该边的新图的k2-MDD.

5) 删除边

根据要删除边的起止顶点v1和顶点v2的编号得到该条边的编号E(v1,v2)，生成该条边的k2-MDD;然后将原图的k2-MDD与要删除边的k2-MDD进行DIFFERENCE运算，即得到删除了该边的新图的k2-MDD.DIFFERENCE是求2个MDD的差运算，执行函数apply(DIFFERENCE,A,B,res)后，res={x|x∈A且x∉B}.

根据上述图的基本操作，可以很方便地拓展到图的一些复杂操作，比如图中宽度优先搜索、求最短路、网络流等.

4 算法复杂度分析

由边编码集合构造k2-MDD以及基于k2-MDD的有向图的添加和删除边，由于涉及到MDD的初始化、生成、求交集、求并集及化简等运算过程，在文献[9]中已经进行了复杂度分析，这里不再分析.

在构造k2-MDD时，对图的单个顶点编码的时间复杂度为O(logk|V|)；同理，对图的单条边编码的时间复杂度也是O(logk|V|)；因此对图的所有边进行编码的时间复杂度即为O(|E|logk|V|).

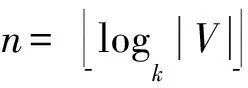
对于大规模图数据存储于操作，在实际应用中，通常评价指标是存储结果和查询时间，对于构造时的复杂度一般并不关心.

5 实验与分析

本文利用MEDDLY库，采用C++语言实现所提出的算法.实验用机器配置的软件平台为Ubuntu14.04 LTS 64位操作系统(内核Linux 3.19.0-61-generic)，硬件平台为Intel®CoreTMi5-4690 CPU @ 3.50 GHz处理器，8 GB内存.测试数据采用公开的真实数据集和随机数据集.真实数据集使得实验结果具有更好的代表性，随机数据集可以看出存储结构在不同规模图数据下的节点数变化趋势.

5.1 基于真实数据集的实验

表1列出了测试中使用的真实网页图和社交网络数据，数据均来自米兰大学LAW(Laboratory for Web Algorithmics)[12].表1分别给出了这些数据集的顶点数、边数、顶点数与边数的比值以及这些数据集在网站的文件名.

Table 1 Description of Testing Real Graphs

在网页图中同一个域内的网页之间的链接数比较多，而域之间的链接数就比较少，其具备2个特征：

1) 本地性.大多数链接都是域内的，它们通常会指向字典序比较靠近的页面.

2) 相似性.在字典序中邻近页面的邻居集合也是相似的.

而社交网络图并不可以直接对其中的节点进行排序，但是也包含着类似于网页图体现的特征，例如同一个社区内的好友关系数量比较多，而社区之间的好友关系数量就比较少.

对于这些真实数据集的特性，本文提出的k2-MDD结构正好可以发挥其同构子树合并的优势.

针对这些数据集，分别使用k2树、k2-MDD以及有序二叉决策图(ordered binary decision diagram, OBDD)[10]共3种方法进行了测试.表2给出了这些数据集在上述3种方法下的实验结果，表2中的数据为这3种存储结构的节点数.

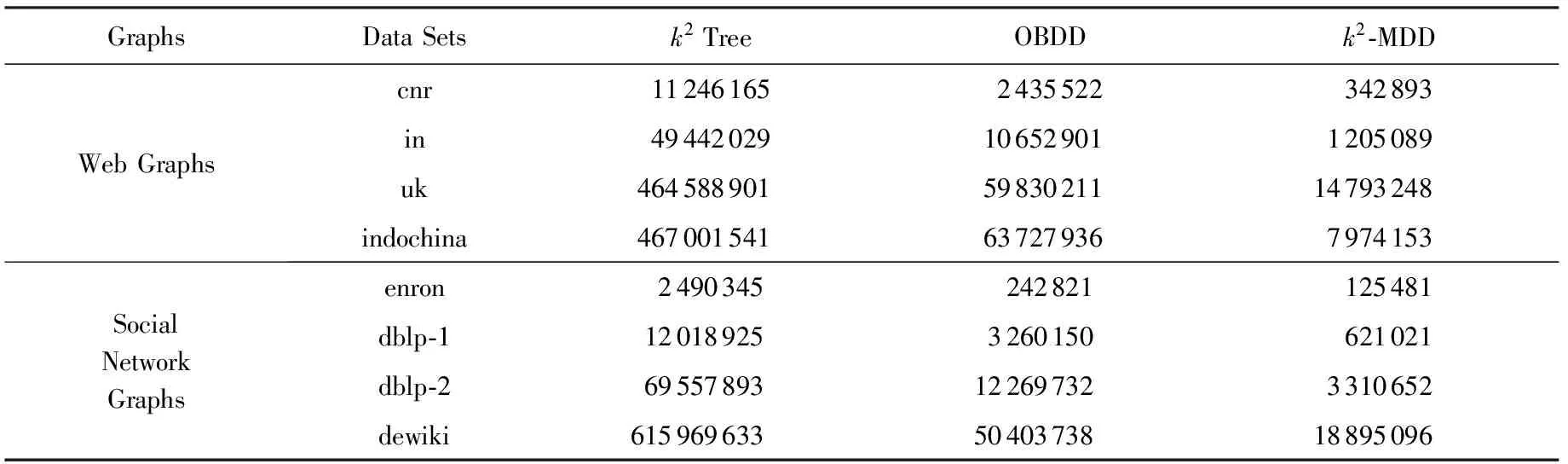
Table 2 The Experimental Results

5.2 基于随机数据集的实验

除上述真实数据集外，我们随机生成了11组图数据，顶点数均为1 000，边数分别为10 000，100 000，200 000，…，900 000，1 000 000.这些图中顶点之间的连接关系完全随机，因此没有网页图和社交网络的特性.需要说明的是，当边数为1 000 000时，图为完全图.图13给出了k2树和k2-MDD在这些随机数据集上的实验结果.

Fig. 13 The experimental results of the random graphs.图13 随机图实验结果

5.3 实验分析

对于真实数据集，从表2的实验结果中的数据可得，在选用的4组网页图上，k2-MDD的节点数平均仅为k2树的2.59%；在选用的4组社交网络上，k2-MDD的节点数平均仅为k2树的4.51%.可以看出使用k2-MDD结构来存储图可以大大减少节点数量，达到了预期效果.另外，还可以看到，OBDD结构在存储图时，节点数也比k2树大大减少，这也体现出了决策图在节点合并方面的优势.

对于随机数据集，从图13的实验结果中的数据可以看出，在图的顶点数不变的情况下，随着边数增多，即图变的越来越稠密，k2树的节点数在持续增加，而k2-MDD的节点数在图的边数达到完全图的一半之后开始减少.这说明k2树只适用于稀疏图，而k2-MDD不仅适用于稀疏图还适用于稠密图.因为k2树只对某节点的指针全部指向0节点的情况进行了合并，所以造成了这样的结果.

在查询时间方面，由于边查询的时间复杂度与k2树相同，而同等规模的图，k2-MDD与k2树结构的高度也相同，因此查询时间不相上下.通过对真实数据集和随机数据集进行实验验证也确是如此.因此本文未给出k2-MDD与k2树在查询时间方面的数据对比.

6 结束语

本文提出了一种新的图数据的表示方法——k2-MDD，这种存储结构的设计跟传统思想有所区别.k2-MDD把有向图的邻接矩阵进行k2划分后，转化为多值布尔函数并使用基于MDD的相关逻辑运算对有向图进行操作.实验表明：在处理真实数据集时，k2-MDD的节点数比k2树大大减少，优势相当明显；在处理随机数据集时，k2-MDD不仅适用于稀疏图，同样也适用于稠密图.当存储结构变得紧凑之后，对于图的相关计算的复杂度也会相应地变低.文中给出了k2-MDD对图的边进行增加与删除的操作，稍加拓展，即可得到对顶点的添加与删除以及对子图的添加与删除，因此本结构适用于动态图.图数据的k2-MDD表示，既具有k2树表示的紧凑型和查询的高效性，又能实现符号决策图表示下图模式的高效操作，从而实现了描述和计算能力的统一.

[1]Angles R, Gutierrez C. Survey of graph database models[J]. ACM Computing Surveys, 2008, 40(1): 1-39

[2]Robinson I, Webber J, Elfrem E. Graph Databases[M]. Sebastopol, CA: O’Reilly Media Press, 2015

[3]Zhang Yu, Liu Yanbing, Xiong Gang, et al. Survey on succinct representation of graph data[J]. Journal of Software, 2014, 25(9): 1937-1952 (in Chinese)(张宇, 刘燕兵, 熊刚, 等. 图数据表示与压缩技术综述[J]. 软件学报, 2014, 25(9): 1937-1952)

[4]China Internet Network Information Center. The 37th statistical report on Internet development in China[EB/OL]. 2016[2016-01-31]. http://www.cnnic.net.cn/hlwfzyj/hlwxzbg/hlwtjbg/201601/t20160122_53271.htm (in Chinese)(中国互联网络信息中心. 第37次中国互联网络发展状况统计报告[EB/OL]. 2016[2016-01-31]. http://www.cnnic.net.cn/hlwfzyj/hlwxzbg/hlwtjbg/201601/t20160122_53271.htm)

[5]Brisaboa N R, Ladra S, Navarro G.k2-trees for compact Web graph representation[C] //Proc of the 16th Int Symp on String Processing and Information Retrieval. Berlin: Springer, 2009: 18-30

[6]Brisaboa N R, Ladra S, Navarro G. Compact representation of Web graphs with extended functionality[J]. Information Systems, 2014, 39(1): 152-174

[7]Shi Quan, Xiao Yanghua, Lu Yiqi, et al. Towards optimizingk2-tree for large-scale graph storage[J]. Application Research of Computers, 2011, 28(7): 2488-2491 (in Chinese)(施佺, 肖仰华, 鲁轶奇, 等. 基于k2树的大图存储优化研究[J]. 计算机应用研究, 2011, 28(7): 2488-2491)

[8]Shi Quan, Xiao Yanghua, Bessis N, et al. Optimizingk2-trees: A case for validating the maturity of network of practices[J]. Computers & Mathematics with Applications, 2012, 63(2): 427-436

[9]Srinivasan A, Ham T, Malik S, et al. Algorithms for discrete function manipulation[C] //Proc of ICCAD-90. Piscataway, NJ: IEEE, 1990: 92-95

[10]Gu Tianlong, Xu Zhoubo. Ordered Binary Decision Diagram and Its Application[M]. Beijing: Science Press, 2009 (in Chinese)(古天龙, 徐周波. 有序二叉决策图及其应用[M]. 北京: 科学出版社, 2009)

[11]Iowa State University Research Foundation. MEDDLY: Multi-terminal and edge-valued decision diagram library, Version 0.11.486[CP/OL]. 2014[2015-10-02]. http://meddly.sourceforge.net/index.html

[12]Department of Computer Science, University of Milan. Laboratory for Web algorithmics[DB/OL]. 2015[2015-11-01]. http://law.di.unimi.it/datasets.php

Dong Rongsheng, born in 1965. Professor. Senior member of China Computer Federation. His main research interests include protocol engineering and wirless sensor networks.

Zhang Xinkai, born in 1991. Master candidate. His main research interests include graph data representation and symbolic technology.

Liu Huadong, born in 1978. Lecturer. His main research interests include graph data representation and symbolic technology.

Gu Tianlong, born in 1964. PhD, professor, PhD supervisor. Senior member of China Computer Federation. His main research interests include formal method, formal computing and knowledge engineering.

Representation and Operations Research of k2-MDD in Large-Scale Graph Data

Dong Rongsheng, Zhang Xinkai, Liu Huadong, and Gu Tianlong

(Guangxi Key Laboratory of Trusted Software (Guilin University of Electronic Technology), Guilin, Guangxi 541004)

Efficient and compact representation and operation of graph data which contains hundreds of millions of vertices and edges are the basis of analyzing and processing the large scale of graph data. Aiming at the problem, this paper proposes a representation of large-scale graph data based on the decision diagram, that isk2-MDD, providing the initialization ofk2-MDD and the basic operation such as the edge query, inner(outer) neighbor query, finding out(in)-degree, adding(deleting) edge, etc. The representation method is optimized and improved on the basis ofk2tree, and after dividing the adjacency matrix of graph intok2, it is stored with the multi valued decision diagram, so as to achieve a more compact storage structure. According to the experimental results of a series of real Web graph and the social network graph data (cnr-2000, dewiki-2013, etc.) derived from the LAW laboratory at the University of Milan, it can be seen that the number ofk2-MDD’ nodes is only 2.59%-4.51% of thek2tree, which achieving the desired effect. According to the experimental results of random graphs, it can be seen that thek2-MDD structure is not only suitable for sparse graphs, but also for dense graphs. The graph data ofk2-MDD shows that both containing the compact and query efficiency representation ofk2tree and realizing the efficient operation of the graph model can thus achieve the unity of description and computing power.

graph data; storage optimization;k2-MDD;k2tree; decision diagram

2016-08-15；

2016-10-28

国家自然科学基金项目(U1501252,61363070,61572146,61363030)；广西高等学校高水平创新团队及卓越学者计划；桂林电子科技大学创新团队资助项目 This work was supported by the National Natural Science Foundation of China (U1501252, 61363070, 61572146, 61363030), the High Level Innovation Team of Guangxi Colleges and Universities and Outstanding Scholars Fund, and the Program for Innovative Research Team of Guilin University of Electronic Technology.

古天龙(gu@guet.edu.cn)

TP311