书本图的BC-子树计数及渐进密度特性分析∗
2019-12-27孙道强刘永梅王文虎袁日强刘淼淼
孙道强 刘永梅 王文虎 危 星 袁日强 刘淼淼
(1.平顶山学院计算机学院 平顶山 467000)(2.平顶山学院财务处 平顶山 467000)
1 引言
图的结构及相关拓扑参数的研究具有重要的理论意义和应用背景[1~4],比如,网络特性的分析、化合物同分异构体的分辨、分子的物理化学性质的预测、活性影响的定量研究、材料和药物合成。据不完全统计,目前大约有四百多项拓扑指标。比如,距离型的 Wiener指标[5~6]、Harary 指标[7],结构型的子树数指标[8](即,一个图的所有非空子树的个数)、BC-子树数指标[9](即,一个图的所有BC-子树的个数,其中BC子树至少含两个顶点,且该子树的任意两片叶子的距离都是偶数的子树)、原子键连通度指标[10](ABC)等。
相对于距离型的Wiener指标,图的结构型BC-子树数指标相对较新,BC树的概念是由著名图论学家Harary等在研究图的核的时候提出的[11],该概念提出后,引起了计算机[12~13]、化学[14~15]等领域国内外学者的关注和研究。
受文献[9,16]中利用生成函数解决BC-子树的方法的启发,本文拟利用生成函数和结构分析的方法,解决书本图Bn,2(n≥2)的BC-子树生成函数,并利用边生成函数分析它的BC-子树密度渐进特性。
2 符号和定义
令 G=(V(G),E(G);f,g)是顶点集 ||V(G)=n ,边集 ||E(G)=m,顶点和边生成函数分别为 f,g一个加权图。G的非空无环的子结构叫做G的子树;若G的一棵子树T同时满足如下定义:含至少两个顶点,且它的任意两片叶间的距离均为偶数,那么T也被叫做G的一棵BC-子树。若无特殊声明,文中我们规定 f:V(G)→ℜ×ℜ,g:E(G)→ℜ,ℜ为实数。记G-X为G的删除集合X后的图。
记L(G)为G的叶子集合,记SBC(G)为G的所有BC-子树的集合,记S(G;v)为G的含顶点v的子树集合。对于任一个顶点vk和一个子树T1∈S(G;vk),定义 T1的 w_vodd权重(记为w_vodd(T1))如下:若T1是一个单独的加权顶点,那么w_vodd(T1)等于vk的奇权重;否则,w_vodd(T1)等于SO(T1)中每个顶点的偶权重,SE(T1)中每个叶子(非子叶)顶点的奇权重((1+奇权重)),以及T1中每条边的权重的乘积。
同样地,定义 T1的 w_veven权重(记为w_veven(T1))如下:若T1是一个单独的加权顶点,那么w_veven(T1)等于vk的偶权重;否则,Pn=(V(Pn),E(Pn);f,g)等于 SE(T1)中每个顶点的偶权重;SO(T1)中每个叶子(非叶子)顶点的奇权重((1+奇权重)),以及T1中的每条边的权重的乘积。这里
SO(T1)={v|v∈V(T1)∧dT1(v,vk)≡1(mod 2)}
SE(T1)={v|v∈V(T1)∧dT1(v,vk)≡0(mod 2)}。
S(G;vk)的子树的奇,偶生成函数,分别记做F(G;f,g,vk,odd),F(G;f,g,vk,even),为
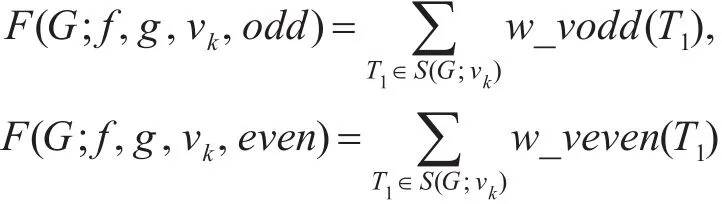
同样地,对于加权图G的一棵BC-子树T2,定义
BES(T2)={v|v∈V(T2)∧dT2(v,vl)≡0(mod 2)}
和
BOS(T2)={v|v∈V(T2)∧dT2(v,vl)=1(mod 2)}
其中vl∈L(T2)。定义T2的BC-权重wbc(T2),为BES(T2)中顶点的偶权重和T2的所有边的权重的乘积。定义加权图G的BC-子树生成函数,记作
由上面的符号定义,可知 ηBC(G)=F(G;(0,1),1)为G的BC-子树数。
为方便叙述,我们引入以下引理,令T=(V(T),E(T);f,g)为n(n>1)个顶点的加权树,vi是T的一个顶点,u≠vi是T的叶子且e=(u,v)为对应的悬挂边。构造加权树 T′=(V(T′),E(T′);f′,g′)如下:V(T′)=V(T){u},E(T′)=E(T){e},且
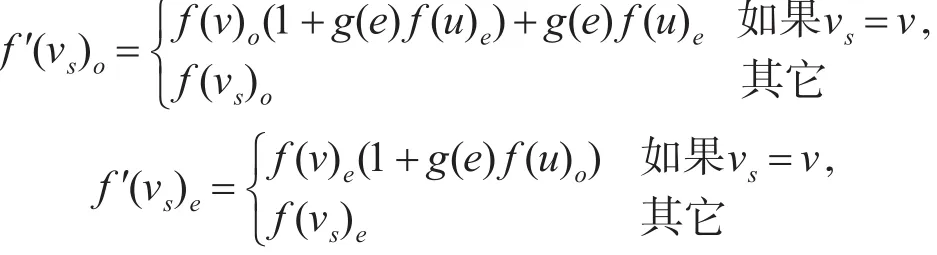
对任意 vs∈V(T′) ,g′(e)=g(e)(e∈E(T′)),这里,f(v)o(f′(vs)o) 和 f(v)e(f′(vs)e) 分别代表顶点v(vs)的奇权重和偶权重。
引理 1[9]:由上述定义和符号,可得
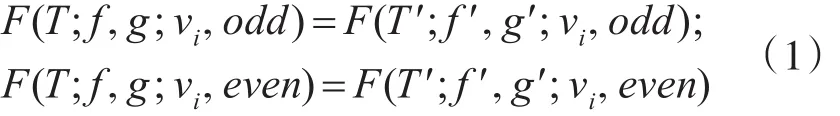
引理2[9]:令T为一棵加权树,u和v为它的两个不同的顶点,记Puv=ux1x2…xl-1v为T的连接u和 v 的路径,长度为 l,此外,记 Tu, Tv, Txi(i=1,2,…l-1)为T的删除路径 Puv上的所有边后含u, v, xi的加权图。则当l为奇数时
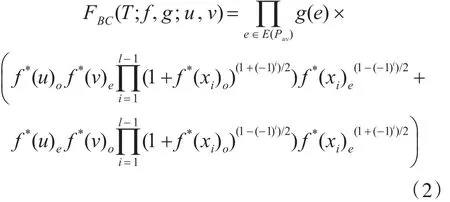
当l为偶数时

这 里 f*(vˉ)o=F(Tvˉ;f, g;vˉ, odd) ,f*(vˉ)e=F(Tvˉ;f,g;vˉ,even),对于 vˉ∈{u,v,xi(i=1,2,…,l-1)}。
由引理1和2,及BC-子树的定义,对于树T=(V(T),E(T);f,g)的一棵子树 Ts,按照引理 1 的方式迭代的收缩加权树T的叶子节点到子树Ts的某个顶点,直到收缩为树Ts为止,此时,我们得到一 棵 加 权 树,其 中。可得含Ts的BC子树的生成函数如下。
定理 1:令 Ts为加权树 T=(V(T),E(T);f,g)的一棵子树,加权树为按引理1的方式迭代T的叶子节点变成的树,则T的含子树Ts的BC-子树的生成函数为
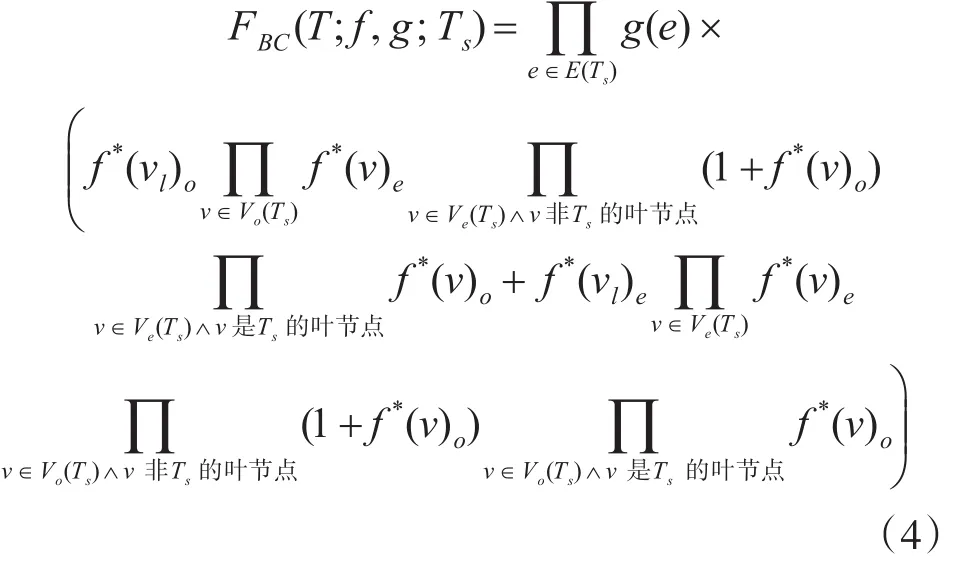
其中vl为Ts的某一个叶子顶点,且Vo(Ts)={v|v∈V(Ts)∧dTs(v,vl)≡1(mod 2)} , Ve(Ts)={v|v∈V(Ts)∧dTs(v,vl)≡0(mod 2)}。
接下来研究书本图的BC-子树问题,书本图的定义如下。

图1 书本图 Bn,2(n≥2)
定义1:将长度为3的n条路径的首尾顶点用一条边进行连接,由此产生的图我们称之为书本图,记为 Bn,2(n≥2),如图1所示,易知,n页书本图有2n+2个顶点和3n+1条边。
3 书本图 Bn,2(n≥2)的BC-子树
定理 2:令 Bn,2=(V(Bn,2),E(Bn,2);f,g) 为 n 页加权书本图(见定义2.4和图1),顶点和边的权重函 数 分 别 为 f(v)=(0 ,y)(v∈V(Bn,2)) 和 g(e)=z(e∈E(Bn,2)),则
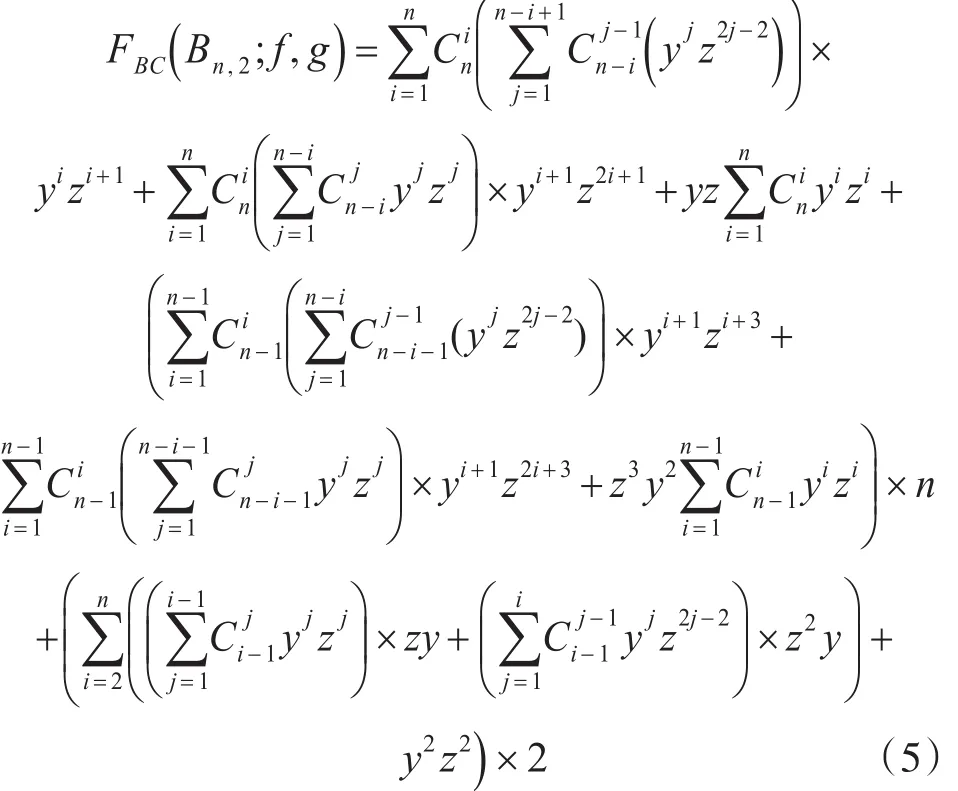
证明:将 Bn,2的BC-子树分为如下两种情况。
1)含公共边 (u,v);
2)不含公共边 (u,v)。
对于第1)种情况,根据BC-子树的结构特性,我们继续将它分为三类。

对于类(2)的情况,根据定理1,可得其BC-子树的生成函数为
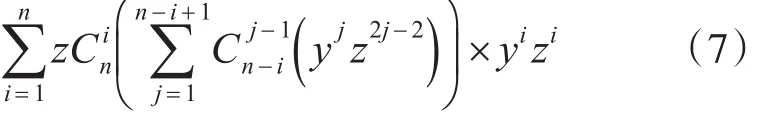
同类(2)的情况一样,可得类(3)对应的BC-子树生成函数为

对于第2)种情况,将它的BC-子树也分为四类:
(4)含u点但不含v点的BC-子树;
(5)含v点但不含u点的BC-子树;
(6)u和v两点都不含的BC-子树;
(7)u和v两点都含的BC-子树;
由文献[9]算法4可知类(4)和类(5)的BC-子树生成函数
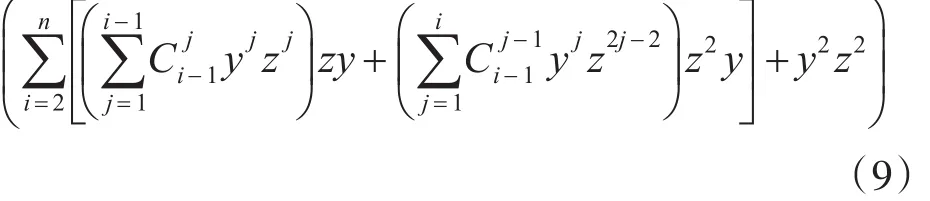
易知类(6)是n个路径树P2所对应的BC-子树生成函数,由文献[9]可知,它的值为0。
类似于第1)种情况的证明,可得类(7)的BC-子树生成函数为

综合式(6)~(10),定理得证。
将权重函数y,z分别替换为1,可得
推论1:书本图 Bn,2(n≥2)的BC-子树数为

4 书本图的BC-子树密度

将顶点和边的权重分别初始化为(0,1)和z,由定理2,可得书本图Bn,2的BC-子树边生成函数为
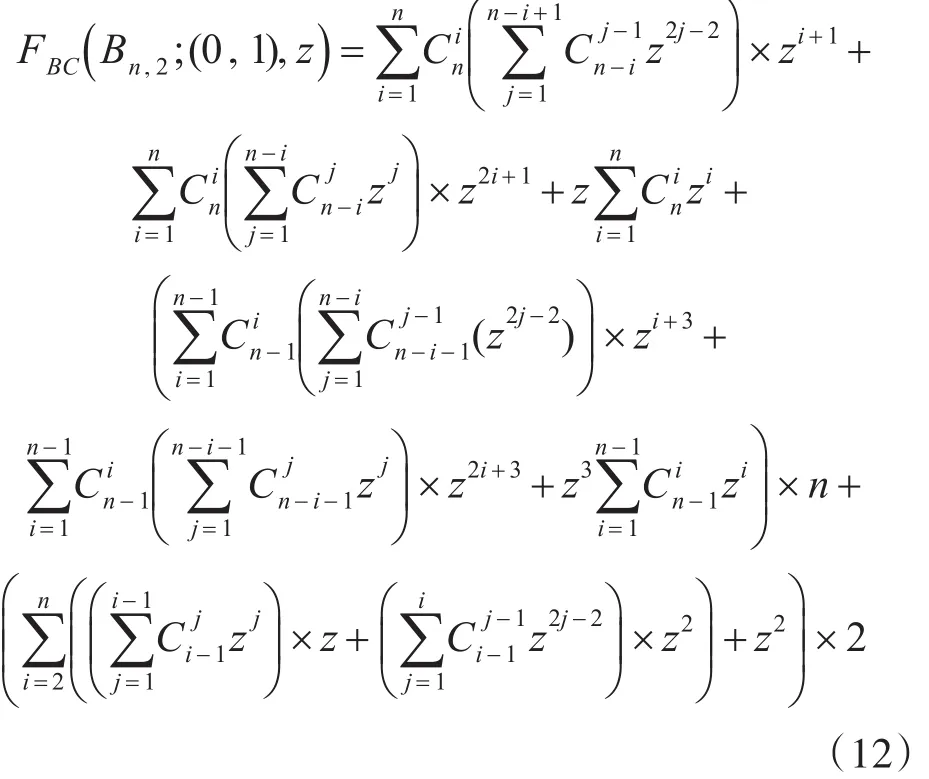
根据BC-子树密度的定义,可得书本图Bn,2的BC-子树密度为

观察图2可知,书本图 Bn,2(n≤100)的书本图Bn,2(n≤100)的BC子树密度随着n的增大不断减小。

图2 书本图Bn,2(n≤100)的BC-子树密度
5 结语
本文利用生成函数和结构分析的方法,给出了书本图Bn,2(n≥2)的BC-子树生成函数,并简要分析了Bn,2(n≥2)的BC-子树密度的渐进特性,研究为探索复杂圈图和分子的新的结构特性提供了理论基础。
