基于广义高斯分布的贝叶斯概率矩阵分解方法
2016-12-22燕彩蓉张青龙黄永锋
燕彩蓉 张青龙 赵 雪 黄永锋
(东华大学计算机科学与技术学院 上海 201620)(cryan@dhu.edu.cn)
基于广义高斯分布的贝叶斯概率矩阵分解方法
燕彩蓉 张青龙 赵 雪 黄永锋
(东华大学计算机科学与技术学院 上海 201620)(cryan@dhu.edu.cn)
贝叶斯概率矩阵分解方法因较高的预测准确度和良好的可扩展性,常用于个性化推荐系统,但其推荐精度会受初始评分矩阵稀疏特性的影响.提出一种基于广义高斯分布的贝叶斯概率矩阵分解方法GBPMF(generalized Gaussian distribution Bayesian PMF),采用广义高斯分布作为先验分布,通过机器学习自动选择最优的模型参数,并基于Gibbs采样进行高效训练,从而有效缓解矩阵的稀疏性,减小预测误差.同时考虑到评分时差因素对预测过程的影响,在采样算法中添加时间因子,进一步对方法进行优化,提高预测精度.实验结果表明:GBPMF方法及其优化方法GBPMF-T对非稀疏矩阵和稀疏矩阵均具有较高的精度,后者精度更高.当矩阵非常稀疏时,传统贝叶斯概率矩阵分解方法的精度急剧降低,而该方法则具有较好的稳定性.
个性化推荐系统;贝叶斯概率矩阵分解;机器学习;广义高斯分布;稀疏矩阵
推荐系统作为一种有效的信息过滤手段,是当前解决信息过载问题及实现个性化信息服务的有效方法之一[1].近几年举办的比赛,如Netflix百万美金大奖赛、KDD CUP 2011音乐推荐比赛、百度电影推荐竞赛以及阿里巴巴大数据竞赛更是把推荐系统的研究推向了高潮.
作为协同过滤推荐系统中的一种新型推荐生成方法,基于矩阵分解(matrix factorization, MF)的潜在因子模型(latent factor model)因准确度高、可扩展性好等因素受到了广泛的关注[2].常用的矩阵分解方法主要包括规范化的SVD(regularized SVD)[3]、非负矩阵分解(nonnegative matrix factorization, NMF)[4]、概率矩阵分解(probabilistic matrix fact-orization, PMF)[5]和贝叶斯概率矩阵分解(Bayesian PMF)[6]等.其中Bayesian PMF从概率的角度探讨矩阵分解的最优化问题,算法的预测准确性比较高,且不需要设定正则化系数,因此得到了广泛应用[7].
现实生活中,数据矩阵往往极其稀疏,以最近热映的电影《魔兽》为例,中国票房14.7亿元,观影人次近4 000万,豆瓣评分人次为129 888,评分密度仅为0.325%.为了缓解数据稀疏问题,学者们提出了社会化推荐(social recommendation)方法[8-9].为了提取更优的潜在特征向量,文献[10]将用户的各种社会网络关系融合到矩阵的优化分解过程中,提出社会化矩阵分解;文献[11]提出因子分解机(factorization machines)模型.然而,用户对项目的评分信息与用户之间的社会关系网络信息往往来源于不同的数据源,因此社会化推荐在推广应用中有一定的局限性[12].
针对矩阵稀疏性影响预测精度的问题,本文在贝叶斯概率矩阵分解的基础上,提出一种基于广义高斯分布的贝叶斯概率分解方法,同时考虑用户评价行为对用户评分的影响会随着时间弱化的情况[13],在方法中添加时间因子,进一步提高预测精度.
1 相关定义
推荐系统中最基本的数据就是关于用户对项目的评分,通过对它们进行分析,了解用户与项目之间的关联,从而实现项目推荐.
定义1. 评分矩阵.假设有用户向量u(大小为n)、项目向量v(大小为m),每个用户对每个项目都可能产生一个评分,其值构成了用户-项目评分矩阵Rn×m.

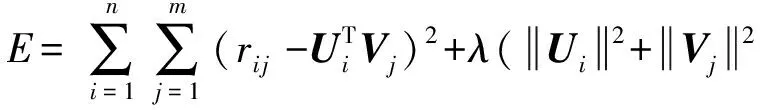
(1)
通常采用随机梯度下降(stochastic gradient descent, SGD)方法优化目标损失函数,当其取最小值时对应的Un×k和Vk×m即为最优解.
定义3. 稀疏矩阵.指矩阵中非零元素占全部元素的百分比很小的矩阵(通常设为5%以下).实际应用中,由于多数用户不会对其所浏览的所有项目做出显式反馈,因此评分矩阵通常是稀疏的.本文主要研究稀疏矩阵的分解.
定义4. 贝叶斯概率矩阵分解.假设用户特征向量矩阵Un×k和项目特征向量矩阵Vk×m服从均值为μU,μV,方差为ΛU,ΛV的高斯分布,用户、项目特征向量矩阵的条件概率分布如下:
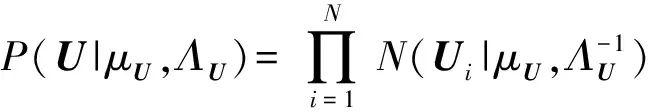
(2)
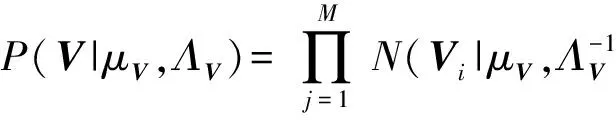
(3)
用户对项目的评分变成一个概率问题:
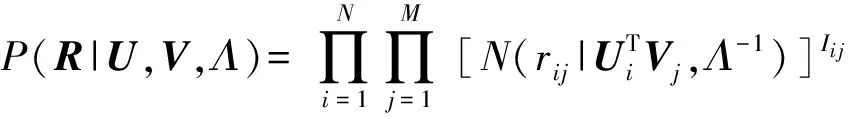
(4)
其中,N(x|μ,Λ-1)是期望为μ、方差为Λ-1的高斯分布,Iij是示性函数;若rij≠0,则Iij=1,否则Iij=0.Bayesian PMF进一步设定ΘU={μU,ΛU},ΘV={μV,ΛV}的先验分布为高斯-威沙特分布(Gaussian-Wishart distribution),将参数{ΛU,ΛV}整合到算法内部,概率调整为
P(ΘU|Θ0)=P(μU|ΛU)P(ΛU)=
N(μU|μ0,(β0ΛU)-1)W(ΛU|ω0,ν0),
(5)
P(ΘV|Θ0)=P(μV|ΛV)P(ΛV)=
N(μV|μ0,(β0ΛV)-1)W(ΛV|ω0,ν0),
(6)
其中:
1)Θ0={μ0,ν0,ω0,Λ,β0};
2)W(Λν|ω0,ν0)是自由度为v0、尺度参数为ω0的威沙特分布.
贝叶斯推断是将先验的思想和样本数据相结合得到后验分布,然后根据后验分布进行统计推断,其精度受样本数量及其先验分布准确性的影响.Bayesian PMF采用高斯分布作为先验分布,对数据比较敏感,当评分矩阵中非零元素较少时,这种方法具有较高的精度,但当评分矩阵非常稀疏时,很难断定样本分布服从高斯分布,其推荐效果不理想[6].本文针对评分矩阵稀疏性不确定问题,提出采用适用范围更加宽泛的广义高斯分布作为先验分布来缓解数据的稀疏问题,提高推荐精度.
Bayesian PMF采用Markov链蒙特卡罗算法(Markov chain Monte Carlo, MCMC)进行训练,该算法具有较低的算法复杂度和较高的检测性能,目前在MCMC方法中最常用的是Gibbs采样(Gibbs sampling)算法.因此,本文在训练基于广义高斯分布的贝叶斯概率矩阵分解方法GBPMF(generalized Gaussian distribution Bayesian PMF)的过程中,使用Gibbs采样算法进行贝叶斯推断.
2 基于广义高斯分布的贝叶斯概率矩阵分解
2.1 广义高斯分布对稀疏数据的影响
广义高斯分布(generalized Gaussian distribution, GGD)的密度函数(probability density function)是广义伽玛分布的密度函数的推广形式,其密度函数定义为[14]
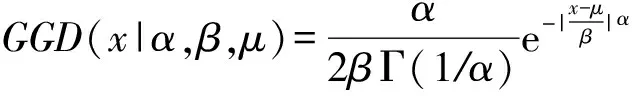
(7)
其中:

3) 参数μ,σ2,α,β分别称为GGD的均值、方差、形状参数和尺度参数.
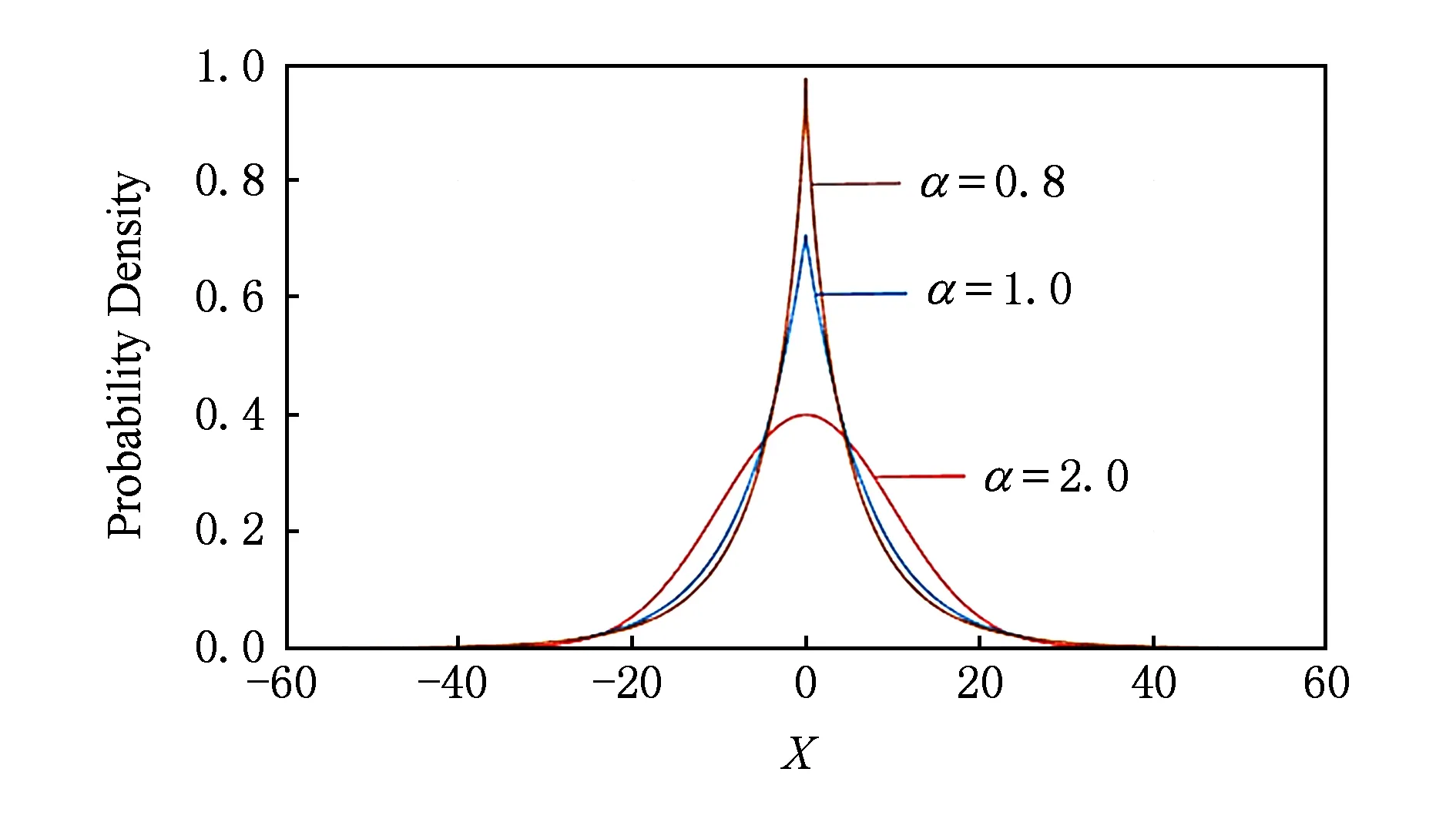
Fig. 1 Probability density comparison of GGD.图1 GGD概率密度变化示例
图1所示为μ=0,σ2=10,α分别为2.0,1.0,0.8的GGD概率密度图.其中纵坐标表示样本的概率分布密度,0点处纵坐标值越大表示样本取0值时的概率密度越大,即样本的稀疏性越大.通过图1所示,我们可以看出:样本的稀疏率与α值呈负相关,即α值越小时,GGD在0附近有越高的峰值;当α=2.0时GGD为高斯分布,我们可以通过调节α值来有效缓解数据的稀疏性.同时,相对于高斯分布,GGD在数据两侧出现的概率较大,这有助于提高推荐系统对项目长尾特性的发掘能力.
针对稀疏矩阵导致推荐结果误差较大的问题,本文提出一种改进的贝叶斯概率矩阵分解方法GBPMF,采用GGD作为用户-项目特征向量矩阵的先验分布来有效缓解矩阵稀疏性.
2.2 GBPMF方法
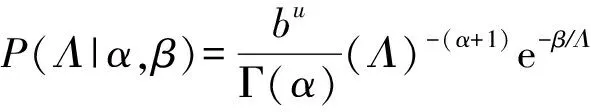
(8)
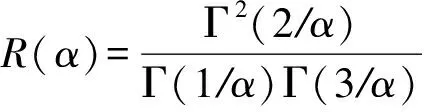

(9)
GBPMF方法的评分矩阵预测过程如下:
1) 根据GGD得到用户特征向量Ui和项目特征向量Vj;
2) 根据逆伽马分布计算高斯分布的方差Λ;
Gibbs采样是一种典型的MCMC算法,适用于联合概率未知,条件概率容易获取的情况.GBPMF方法在训练过程中,采用Gibbs采样进行贝叶斯推断,即利用条件概率构造平稳分布为所求联合概率的Markov链,进行K次抽样,此时的样本{U,V}可近似认为是来自联合概率P(U,V|R,αU,βU,αV,βV)的抽样,最后利用式(10)进行评分预测:

(10)
Gibbs采样的具体过程可以描述为:
1) 对参数Ui进行采样,提取出与之相关的所有变量,利用贝叶斯公式,可得:
P(Ui|R,V,Λ,(αU)i,(βU)i)∝
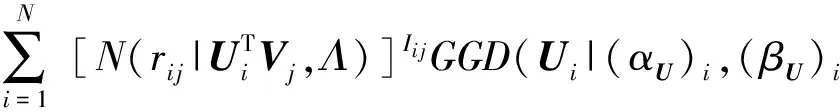
(11)
令P((λU)ki|(αU)ki,(βU)ki)=R((λU)ki|(αU)ki),则有
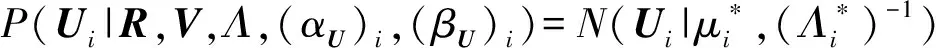
(12)
其中:
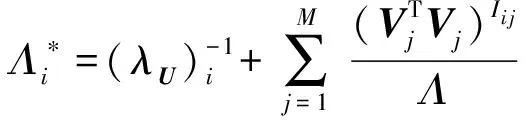
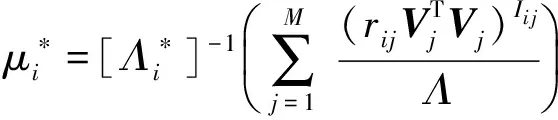
2) 对超参数(λU)i,(αU)i采样,根据贝叶斯公式,可得:
P((λU)i|Ui,(αU)i)∝P(Ui|(λU)i,(αU)i)P((λU)i).
(13)
根据指数函数的性质,可以得到(λU)i服从逆高斯分布(inverse Gauss distribution)
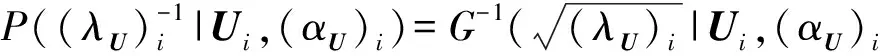
(14)
对广义高斯分布的形状参数(αU)i,它的条件概率满足广义逆高斯分布
P((αU)i|Ui,(λU))=GIG(γ+1,(λU)i+a,b),
(15)
其中,a,b为常数,本文为了计算方便,取γ=0.5将广义逆高斯分布简化为逆高斯分布.
U和V具有对称性,采样具有相同的形式.
3) 对参数Λ进行采样.参数Λ的条件概率形式为
P(Λ|R,U,V)=Γ-1(aΛ,bΛ),
(16)
其中:
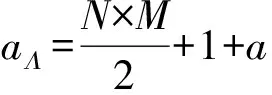
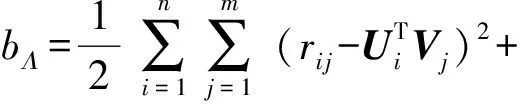
GBPMF的Gibbs采样算法见算法1所示.
算法1. GBPMF的Gibbs采样算法.
输入: 原始评分矩阵R、采样数目K、迭代次数D;
输出:K个样本点.
① 初始化算法参数(U1,V1);
② for每一个采样点do
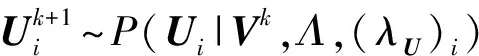
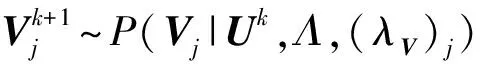
⑤ 根据式Λ~P(Λ|R,U,V)对参数Λ进行采样;
⑥ end for
⑦ 返回K个采样点(U1,V1),(U2,V2),…,(Uk,Vk).
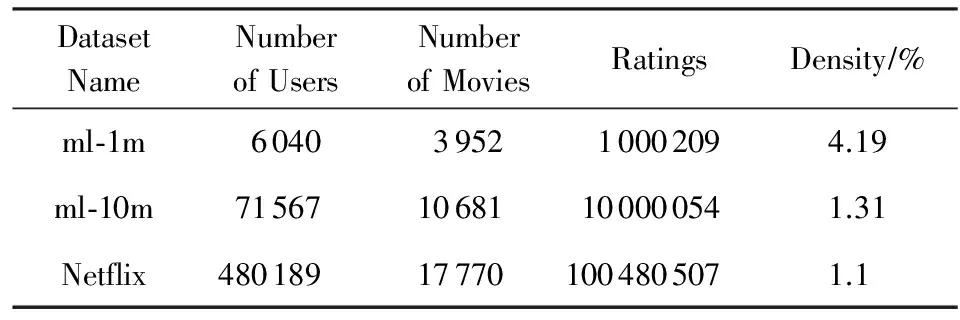
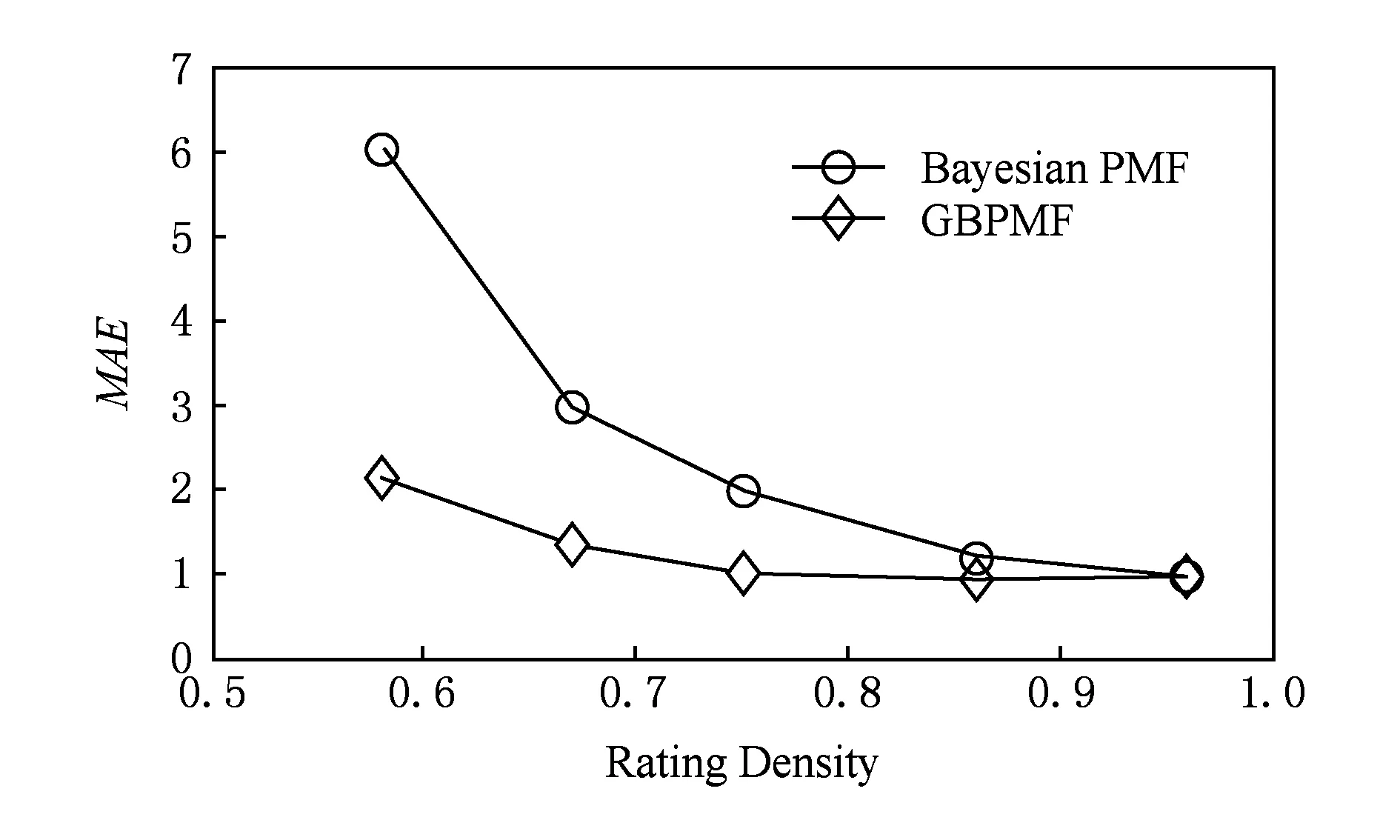
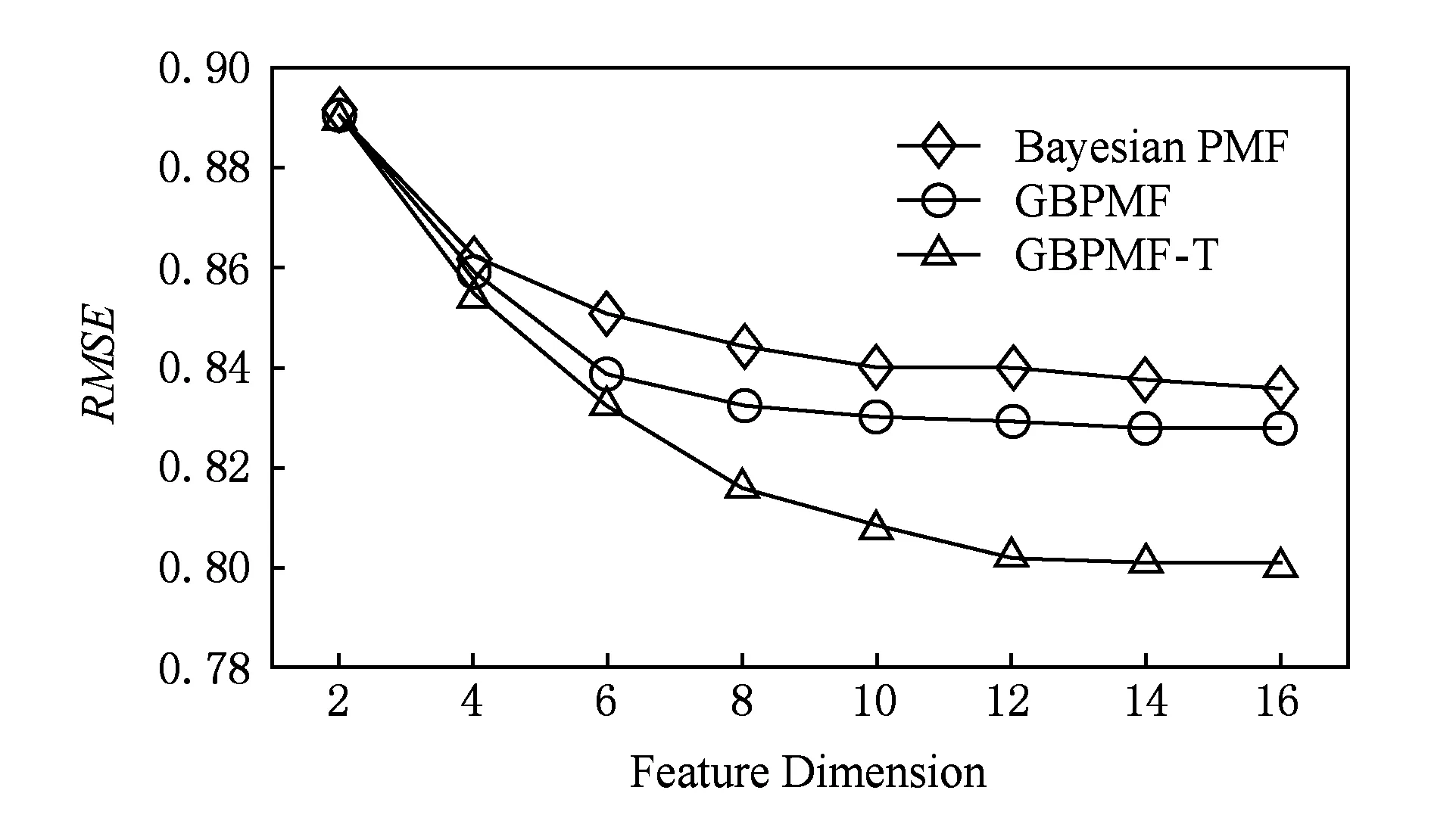
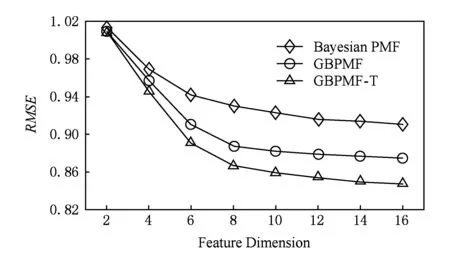
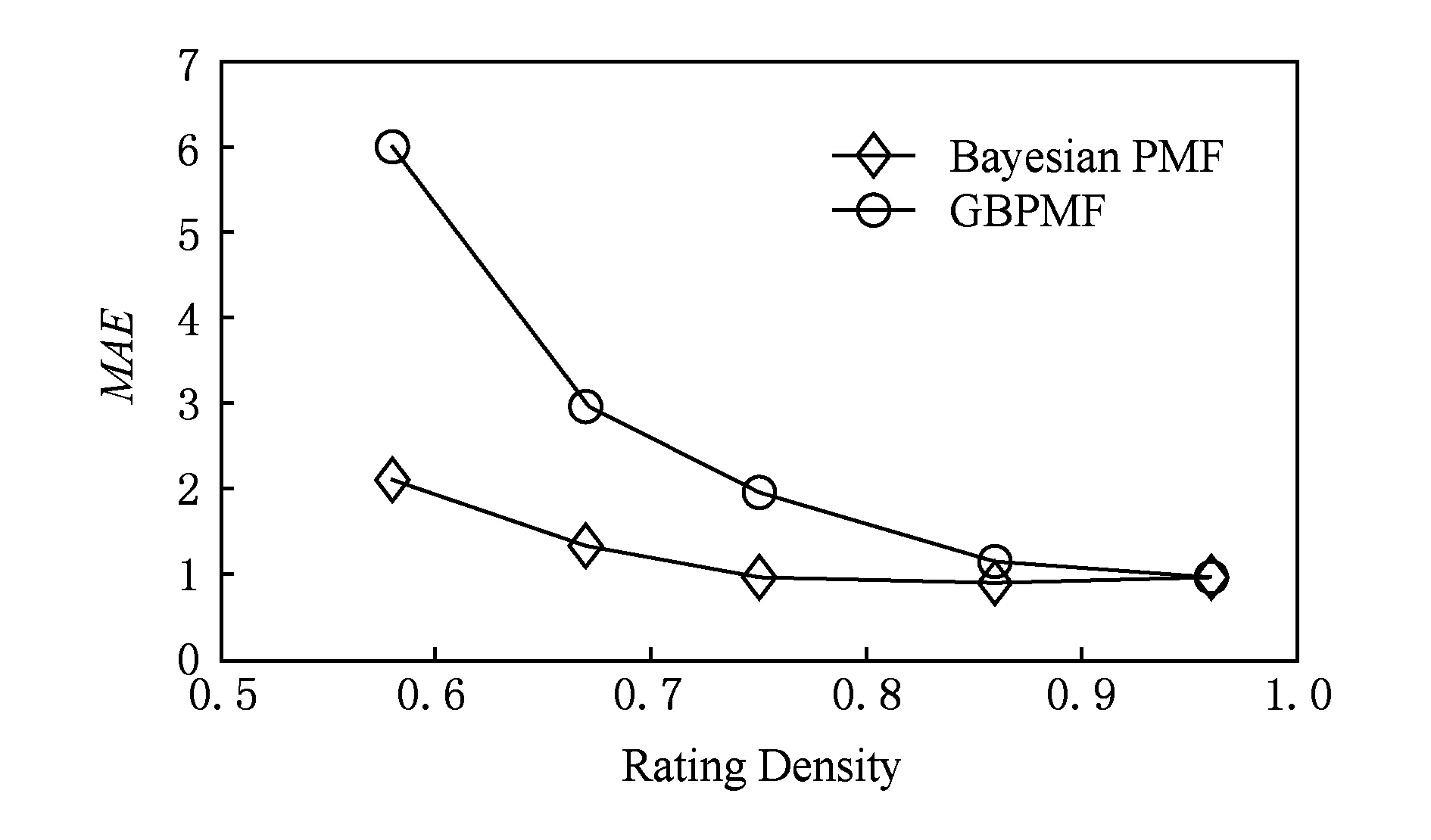
每次Gibbs采样的时间为K×max(m,n),假设迭代D次,则采样时间为D×K×max(m,n);又矩阵分解的运行时间是F×S×p,其中F为用户对物品的评分记录数,p为分解维度,S为迭代次数[16].故整个模型的运行时间为D×K×max(m,n)+F×S×p.通常情况下,D×K×max(m,n) GBPMF方法在处理时不考虑评分产生的时间因素.实际应用中,评分产生的时间因素能够反映用户的行为变化,因而对预测有较大影响.这点在已有的矩阵分解模型中没有考虑到.本文通过在采样算法中添加评分时差因素来进行调优,优化后的方法简称为GBPMF-T,处理过程如下: 1) 为GBPMF模型添加偏置项: bij=μ+bi+bj, (17) 2) 参考文献[17]建立邻域模型,此时预测评分为 (18) 3) 为了提高推荐准确率,对权重矩阵进行0-1标准化,即: (19) 文献[18]已经证明,对权重矩阵标准化处理可以有效提高评分预测准确率. 4) 将评分时差融入到基于领域的算法中,修正相关参数,建立算法为 (20) 其中,Δt=tij-til表示用户i对项目j和项目l的评分时差;f(ωj l,Δt)是一个考虑了时间衰减后的相似度函数,它的主要目的是建立用户行为与评分时差的函数,提高用户最近行为在推荐系统中的权重. 5) 定义f为 (21) 6) 加入时间信息后的目标损失函数为 (22) 其中,λ2是为防止过拟合添加的正则化参数. (23) 同样我们可以用Gibbs采样对GBPMF-T方法进行贝叶斯推断.此时,K次抽样时的样本{U,V,X,Y}可认为是来自联合概率P(U,V,X,Y|R,αU,βU,αV,βV,αX,βX,αY,βY)的抽样,其近似计算为 (24) 由于X,Y和U,V类似,可以按式(12)进行采样.此时参数Λ的条件概率形式为 P(Λ|R,U,V,X,Y)=Γ-1(aΛ,bΛ), (25) 其中: GBPMF-T的Gibbs采样算法见算法2所示. 算法2. GBPMF-T的Gibbs采样算法. 输入: 原始评分矩阵R、时间矩阵T、数目K、迭代次数D; 输出:K个样本点. ① 初始化算法参数(U1,V1,X1,Y1); ② for每一个采样点do ⑦ 根据式Λ~P(Λ|R,U,V,X,Y)对参数Λ进行采样; ⑧ end for ⑨ 返回K个采样点(U1,V1,X1,Y1),(U2,V2,X2,Y2),…,(Uk,Vk,Xk,Yk). 整个模型的时间复杂度为O(F×S×p),这和Bayesian PMF方法的时间复杂度一样. 4.1 数据集和评价标准 实验采用ml-1m数据集、ml-10m数据集和Netflix数据集作为测试数据集来检验GBPMF和GBPMF-T方法的预测精度.MovieLens数据集为用户对自己看过的电影进行评分的数据集,评分分值为1~5.MovieLens数据集包括2个不同大小的库,小规模的库ml-1m数据集是6 040个用户对3 900部电影的大约100万次评分;大规模的库ml-10m数据集是71 567个用户对10 681部电影的大约1 000万次评分的数据.Netflix数据集来自于电影租赁网Netflix的数据库,包含了480 189个匿名用户对大约17 770部电影作出的大约1亿次评分.3个数据集的统计信息如表1所示: Table 1 Information of the Datasets 实验使用的主要评价标准是在推荐预测系统中常用的均方根误差(root mean square error,RMSE)和平均绝对误差(mean absolute error,MAE).RMSE,MAE值越小,表示算法性能越好.RMSE定义为 (26) MAE采用绝对值计算预测误差,定义为 (27) 本文设计了3组实验对经典Bayesian PMF,GBPMF,GBPMF-T性能进行对比. 实验运行硬件平台为Inter®CoreTMi5-4460 CPU @ 3.20 GHz、15.6 GB内存、976 GB硬盘、64位Ubuntu 15.1操作系统,编译软件为IntelliJ IDEA,算法编程语言为Python. 4.2 实验结果与分析 实验分别将ml-1m数据集、ml-10m数据集和Netflix数据集,按照9∶1的比率随机划分为训练集和测试集,实验运行10次,结果取平均值.考虑到时间和精度问题,经过多次实验,我们设置学习速率为0.05,初始化正则参数为0.01. 由于整个实验所采用的3个影响因子相互独立,在实验设计时,我们主要考虑单个因子对实验结果的影响. A组实验考虑Gibbs采样迭代次数对实验结果的影响,选取ml-1m数据集测试,依次增大Gibbs采样迭代次数,直到Bayesian PMF和GBPMF测试的MAE值趋于收敛.不失一般性,实验选取矩阵分解特征维数为10,实验结果如图2所示: Fig. 2 MAE comparison on Gibbs iterations.图2 Gibbs采样次数对性能的影响 从图2中可以看出,相对于Bayesian PMF,GBPMF进行Gibbs采样,MAE值趋于稳定,需要的迭代次数更少.通过第2节对Gibbs采样算法时间复杂度的分析可知,Gibbs采样耗时与迭代次数成正相关.可见,相对于经典Bayesian PMF,GBPMF在运行时间上具有一定的优势. 我们设计B组实验测试矩阵分解特征维数对模型性能的影响.实验选取3种不同的数据集,以RMSE值作为最终测评标准,其中Gibbs采样迭代次数取50,实验结果如图3,4所示: Fig. 3 RMSE comparison on ml-1m.图3 ml-1m的RMSE值比较 Fig. 4 RMSE comparison on Netflix.图4 Netflix的RMSE值比较 从图3,4中可以看出,在ml-1m数据集上,与经典Bayesian PMF相比,GBPMF的预测精度提高了1.02%,GBPMF-T的预测精度提高了4.25%;在Netflix数据集上,与经典Bayesian PMF相比,GBPMF的预测精度提高了多少3.83%,GBPMF-T的预测精度提高了6.78%,可见评分时差和偏置因素对推荐系统预测精度的影响很大.另外,由于Netflix数据集的评分密度只有1.1%,小于ml-1m数据集的评分密度(4.19%),我们大胆推测,在数据稀疏的条件下,GBPMF和GBPMF-T算法能够获得更高的精度. 为了验证上述推测,我们只考虑矩阵稀疏性对推荐精度的影响,进行C组实验,利用ml-10m数据集生成评分密度小于1%的测试环境(设定用户对电影评分数量的阈值为num_m.若用户评分记录数量小于num_m,评分记录取实际评分数量;若用户评分数量大于num_m,随机抽取num_m条评分记录).实际应用中的评分密度一般都小于1%,稀疏矩阵可以更好地反映算法提取潜在特征的能力.实验结果如图5所示. Fig. 5 RMSE comparison on sparse matrix.图5 稀疏矩阵的RMSE值比较 从图5中可以看出,在稀疏数据集上(数据稀疏率为0.96%),与经典Bayesian PMF相比,GBPMF的预测精度提高了4.03%,且2种算法在矩阵分解特征维数为16的时候都已经收敛. 在实际的推荐系统中,数据的稀疏性往往小于1%,为了更直观地显示数据的稀疏性,我们设计了D组实验,选择矩阵分解特征维数为16,通过调节num_m的值改变数据集的稀疏性,实验结果如图6所示: Fig. 6 Influence of matrix sparsity on two methods.图6 矩阵稀疏性对Bayesian PMF和GBPMF的影响 通过图6可以看出,随着评分密度的减小,Bayesian PMF和GBPMF的预测精度都在迅速减小,但GBPMF预测精度减小的幅度要小于Bayesian PMF.值得注意的是,当矩阵极其稀疏(<0.5%)时,GBPMF预测精度要远好于Bayesian PMF,从而说明GBPMF能够有效缓解矩阵稀疏性问题. 本文针对稀疏评分矩阵会降低推荐精度的问题,提出基于广义高斯分布的贝叶斯概率矩阵分解方法GBPMF.方法采用广义高斯分布作为先验分布,通过调节参数值来有效缓解数据的稀疏性,也有助于提高推荐系统对项目长尾的发掘能力;在方法训练过程中,使用Gibbs采样进行贝叶斯推断,适用于联合概率未知,条件概率容易获取的情况;最后通过添加评分时差因子对方法进行优化,进一步提高方法的精度.实验表明:在数据稀疏的情况下,方法仍能保持较高的精度,从而有效提高推荐系统的预测准确率. 在未来的研究中,我们将有效挖掘用户和项目的属性以及属性之间的关系,从而确定有用的隐含特征,进一步提高矩阵分解方法的精度. [1]Goldberg D, Nichols D, Oki B M, et al. Using collaborative filtering to weave an information tapestry[J]. Communications of the ACM, 1992, 35(12): 61-70 [2]Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems[J]. Computer, 2009, 42(8): 30-37 [3]Billsus D, Pazzani M J. Learning collaborative information filters[C] //Proc of the 4th Int Conf on Machine Learning. New York: ACM, 1998: 46-54 [4]Lee D, Seung H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature, 1999, 401(6755): 788-91 [5]Mnih A, Salakhutdinov R. Probabilistic matrix factorization[C] //Proc of the 29th Int Conf on Machine Learning. New York: ACM, 2012: 880-887 [6]Salakhutdinov R. Bayesian probabilistic matrix factorization using MCMC[C] //Proc of the 25th Int Conf on Machine Learning. New York: ACM, 2008: 880-887 [7]Fang Yaoning, Guo Yunfei, Lan Julong. A Bayesian probabilistic matrix factorization algorithm based on logistic function[J]. Journal of Electronics & Information Technology, 2014(3): 715-720 (in Chinese)(方耀宁, 郭云飞, 兰巨龙. 基于Logistic函数的贝叶斯概率矩阵分解算法[J]. 电子与信息学报, 2014(3): 715-720) [8]Wang Zhi, Sun Lifeng, Zhu Wenwu, et al. Joint social and content recommendation for user-generated videos in online social network[J]. IEEE Trans on Multimedia, 2013, 15(3): 698-709 [9]Quijano-Sanchez L, Recio-Garcia J A, Diaz-Agudo B, et al. Social factors in group recommender systems[J]. ACM Trans on Intelligent Systems & Technology, 2013, 4(1): 1199-1221 [10]Jamali M, Ester M. A transitivity aware matrix factorization model for recommendation in social networks[C] //Proc of the 22nd Int Joint Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2011: 2644-2649 [11]Rendle S. Factorization machines[C] //Proc of the 10th IEEE Int Conf on Data Mining. New York: ACM, 2010: 995-1000 [12]Meng Xiangwu, Liu Shudong, Zhang Yujie, et al. Research on social recommender systems[J]. Journal of Software, 2015, 26(6): 1356-1372 (in Chinese)(孟祥武, 刘树栋, 张玉洁, 等. 社会化推荐系统研究[J]. 软件学报, 2015, 26(6): 1356-1372) [13]Koren Y. Collaborative filtering with temporal dynamics[C] //Proc of the 15th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2009: 89-97 [14]Miller J, Thomas J. Detectors for discrete-time signals in non-Gaussian noise[J]. IEEE Trans on Information Theory, 1972, 18(2): 241-250 [15]Wang Taiyue, Li Zhiming. A fast parameter estimation of generalized Gaussian distribution[J]. Chinese Journal of Engineering Geophysics, 2006, 3(3): 172-176 (in Chinese)(汪太月, 李志明. 一种广义高斯分布的参数快速估计法[J]. 工程地球物理学报, 2006, 3(3): 172-176) [16]Xiang Liang. Recommended System Practice[M]. Beijing: Posts & Telecom Press, 1998 (in Chinese)(项亮. 推荐系统实践[M]. 北京: 人民邮电出版社, 2012: 72-73) [17]Koren Y. Factor in the neighbors: Scalable and accurate collaborative filtering[J]. ACM Trans on Knowledge Discovery from Data, 2010, 4(1): 1-24 [18]Karypis G. Evaluation of item-based Top-N, recommenda-tion algorithms[C] //Proc of the 10th Int Conf on Information and Knowledge Management. New York: ACM, 2001: 247-254 Yan Cairong, born in 1978. PhD of Xi’an Jiaotong University. Associate professor and MS supervisor. Member of China Computer Federation. Her main research interests include parallel computing, distributed system and big data analyzing. Zhang Qianglong, born in 1990. MSc. His main research interests include concentrate on personalized recommender, data mining and deep learning. Zhao Xue, born in 1992. MSc. Her main research interests include concentrate on social network analyzing and data mining. Huang Yongfeng, born in 1971. PhD of Shanghai Jiaotong University. Associate professor and MS supervisor. His main research interests include pattern recognition, Internet of things and big data analyzing. A Method of Bayesian Probabilistic Matrix Factorization Based on Generalized Gaussian Distribution Yan Cairong, Zhang Qinglong, Zhao Xue, and Huang Yongfeng (School of Computer Science and Technology, Donghua University, Shanghai 201620) The method of Bayesian probability matrix factorization (Bayesian PMF) is widely used in the personalized recommendation systems due to its high prediction accuracy and excellent scalability. However, the accuracy is affected greatly by the sparsity of the initial scoring matrix. A new Bayesian PMF method based on generalized Gaussian distribution called GBPMF is proposed in this paper. In the method, the generalized Gaussian distribution (GGD) is adopted as the prior distribution model in which some related parameters are adjusted automatically through machine learning to achieve desired effect. Meanwhile, we apply the Gibbs sampling algorithm to optimize the loss function. Considering the influence of the time difference of scoring in the prediction process, a temporal factor is integrated into the sampling algorithm to optimize the method and improve its prediction accuracy. The experimental results show that our methods GBPMF and GBPMF-T can obtain higher accuracy when dealing with both sparse matrix and non-sparse matrix, and the latter can even get better effect. When the matrix is very sparse, the accuracy of Bayesian PMF decreases sharply while our methods show stable performance. personalized recommender systems; Bayesian PMF; machine learning; generalized Gaussian distribution (GGD); sparse matrix 2016-08-15; 2016-10-25 国家自然科学基金项目(61402100);中央高校基本科研业务费专项资金(16D111210) This work was supported by the National Natural Science Foundation of China (61402100) and the Fundamental Research Funds for the Central Universities of China (16D111210). TP3913 基于评分时差的GBPMF方法优化

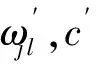
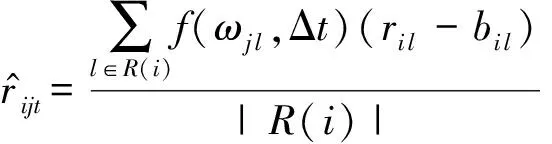
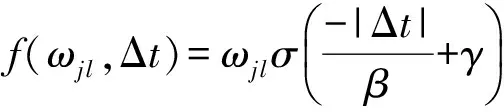

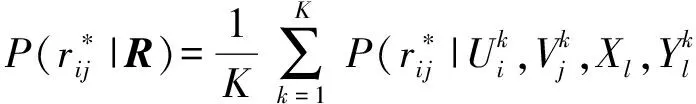
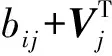


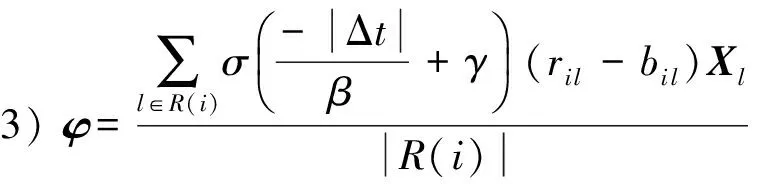
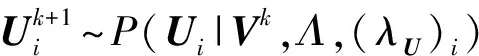
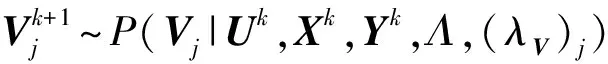

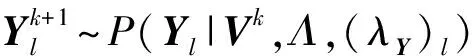
4 实验和结果
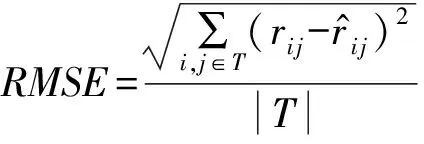
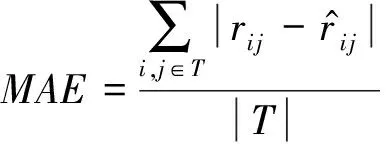
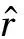

5 结束语




