基于奇异值分解的可分离压缩成像方法
2016-12-22张成汪东沈川程鸿陈岚韦穗
张 成 汪 东 沈 川 程 鸿 陈 岚 韦 穗
1(计算智能与信号处理教育部重点实验室(安徽大学) 合肥 230039)2(安徽省现代成像与显示技术重点实验室(安徽大学) 合肥 230039)(question1996@163.com)
基于奇异值分解的可分离压缩成像方法
张 成1,2汪 东1沈 川1程 鸿1陈 岚1韦 穗1
1(计算智能与信号处理教育部重点实验室(安徽大学) 合肥 230039)2(安徽省现代成像与显示技术重点实验室(安徽大学) 合肥 230039)(question1996@163.com)
可分离压缩传感可以通过一定比例的额外测量有效地解决压缩成像问题中面临的测量矩阵维数过大的瓶颈. 但是现有可分离压缩传感(separable compressive sensing, SCS)方法需要2个可分离的测量矩阵都必须是行归一化后的正交随机矩阵,其显著地限制了该方法的应用范围. 将奇异值分解(singular value decomposition, SVD)方法引入可分离可压缩传感测量过程,可以有效地实现测量矩阵和重建矩阵的分离:在感知阶段可以更多地考虑测量矩阵物理易于实现的性质,如Toeplitz或Circulant等确定性结构的矩阵;在重建阶段,更多地考虑测量矩阵的优化.通过引入奇异值分解对重建阶段的测量矩阵进行优化,可以有效地改善重建性能,尤其是Toeplitz或Circulant矩阵在大尺度图像的压缩重建情形.数值实验结果验证了该方法的有效性.
压缩成像;可分离压缩传感;可分离感知矩阵;奇异值分解;确定性矩阵
压缩成像(compressive imaging, CI)[1-2]是可压缩传感(compressive sensing, CS)[3]理论的一个天然分支.尽管目前已有许多CI的实现方案,但是设计一个有效的CI系统仍然是一个极具挑战性的问题.其主要困难之一是CI的实现过程中涉及到巨大的数据量,这对成像系统的光学设计、校正,数据存储与计算压力等方面都存在深远的影响.
为此,Rivenson等人[4-6]提出将可分离矩阵用于测量系统的设计,提出可分离压缩传感(separable compressive sensing, SCS)方法,该方法可以显著地降低大尺度图像压缩成像时面临的测量矩阵维数问题.但是,Rivenson方法中的可分离矩阵都必须是行归一化后的正交随机矩阵(row-normalized orthogonal random matrix, RNORM)[4],从而导致其在实际成像过程中实现的高难度与高成本.RNORM的独立元素过多,通过硬件实现难度大.
为解决此问题,可以通过引入结构化分离矩阵构造分离矩阵,这样可以降低随机性,但是结构化矩阵的引入同时也会对重建性能造成一定的负面影响.进一步地,本文引入奇异值分解(singular value decomposition, SVD)方法,将测量矩阵和重建矩阵的设计分离:测量矩阵的设计方面更多地考虑其物理可实现的性质;在图像重建阶段,更多地考虑优化重建矩阵的性能,通过对测量矩阵与测量数据的预处理,可以有效地改进重建性能.
1 可压缩传感基本理论
2006年推出的CS理论吸引了理论家的兴趣和从业者的一致好评,成为了一个迅速崛起研究领域.CS提出了一个同步进行信号采样和压缩的新框架.相比经典框架先收集尽可能多的数据然后通过数字压缩丢弃冗余数据技术,CS务求在获取步骤中尽量降低多余的数据集合.
CS的主要研究内容包括稀疏表示、随机投影矩阵和重建算法.
在CS理论中,随机投影矩阵的性质已被广泛研究[7-8].随机投影矩阵Φ的一个特别令人感兴趣的性质是它几乎对所有可能的稀疏基Ψ的选择都是非相干的(incoherent).在CS理论中,信号(图像)可以通过求解下面的1范数最小化的凸优化问题:
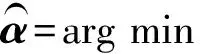
s.t.g=Φf=ΦΨα,
(1)
成像矩阵Φ实际实现时必须考虑3方面的挑战[3-4]:1)可计算性(computational).当测量矩阵的维数较大时的存储与计算问题.2)光学实现(optical implementation).和成像矩阵Φ对应的实际物理实现需要的独立元素数目过大,导致实现难度太大或成本太高.3)标定(calibration).复杂度高的与成像系统的标定工作所需要的工作量较大,标定过程十分繁重与耗时.
2 基于奇异值分解的可分离压缩传感
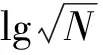
2.1 可分离压缩传感
假定一个可分离矩阵ΦLR可以表示成ΦL⊗ΦR,其中⊗符号表示Kronecker积,可以是直接乘积(direct product)或张量积(tensor product).如果ΦL是一个mL×nL矩阵,ΦR是一个mR×nR矩阵,那么ΦL和ΦR之间的Kronecker积ΦLR∈M×N(M=mLmR,N=nLnR)可以具体表示为
(2)
对于一个nL×nR维矩阵F=[f1f2…fnR],fi∈nL×1(i=1,2,…,nR),可以通过向量化操作将其变成N维列向量,这里向量化采用符号vec(·)来表示,其具体方式是通过堆积多维向量的列来生成:
(3)
考虑二维信号F=[f1f2…fnR]和测量向量G=[g1g2…gmR],gi∈mL×1 (i=1,2,…,mR).F和G是f和g的矩阵表示形式.在这种情形下,式(1)可以写成:
G=ΦLR(F)
①
vec(G)=ΦLRvec(F)=(ΦR⊗ΦL)vec(F)
② Kronecker product
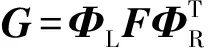
(4)
其中,②是根据Kronecker积的性质得到的.于是,式(1)可以重写成:
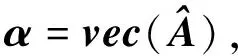
(5)
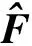
2.2 奇异值分解方法
奇异值分解SVD是谱分解理论在任意矩阵上的推广.考虑一个M×N阶矩阵Φ,则其SVD分解可以表示为
(6)
其中,U是M×M阶正交(酉)矩阵,V是N×N阶正交(酉)矩阵,D是半正定M×N阶对角矩阵.
2.3 基于SVD的可分离压缩传感
结合2.1节中的SCS和2.2节中的SVD,提出了基于SVD的可分离压缩传感方法.首先通过引入结构化分离矩阵(如Toeplitz矩阵和Circulant矩阵等[10])构造分离矩阵,这样可以降低分离测量矩阵的随机性;进一步,引入SVD方法,将测量矩阵和重建矩阵的设计分离:测量矩阵的设计方面更多地考虑其物理可实现的性质,如Toeplitz或Circulant结构等;在图像重建阶段,更多地考虑优化重建矩阵的性能,通过对测量矩阵与测量数据的预处理,可以改进重建性能.
将SVD分别应用于下面的测量模型中的左、右测量矩阵:
(7)
可以得到:
(8)
(9)
其中,UL∈mL×mL,DL∈mL×nL,VL∈nL×nL,D1L∈mL×mL,V1L∈nL×mL,V2L∈nL×(nL-mL),UR∈mR×mR,DL∈mR×nR,VR∈nR×nR,D1R∈mR×mR,V1R∈nR×mR,V2R∈nR×(nR-mR).注意,其中0表示的是由若干个0组成的矩阵.
根据2.2节中的SVD分解,得到的前向测量过程如下:
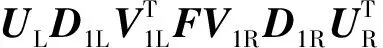
(10)
经过SVD分解处理后的前向测量过程变为
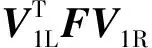
(11)
由于V1L和V1R都是列正交矩阵.
3 数值实验
为验证本文提出方法的有效性,本文设计了4组实验进行了测试.分别是:实验1为测试单次重建实验结果;实验2为不同下采样率重建实验;实验3为不同尺度的重建实验;实验4为鲁棒性测试实验.
测试环境是64 b Win7操作系统, 处理器是Intel®CoreTMi5-2320,4核、主频3.00 GHz, 有效内存8 GB, 测试软件是Matlab2010a.
3.1 实验1:单次重建实验
实验1的目的是通过单次重建实验的结果以验证本文提出方法的有效性.测试图像选用标准Lena图像进行插值放大,最终的测试大小是1792×1792像素.测试Lena图像在ΦL和ΦR分别是行归一化的正交随机矩阵(RNORM),行归一化的随机高斯矩阵(row-normalized random Gaussian matrix, RNRGM)和随机高斯矩阵获得的测量值经过SVD分解(random Gaussian matrix with singular value decomposition, RGM+SVD)处理过后的对比重建结果如图1所示:

Fig. 1 Comparison results of single image reconstruction experiment using different separable measurement matrices.图1 不同可分离测量矩阵单次图像重建实验对比结果
稀疏基Ψ选用Rice大学提供的Daubechies 10的小波基RWT (rice wavelet toolbox)[11],小波尺度为3,本文后续的实验也采用相同的稀疏基设置.单个分离矩阵ΦL和ΦR的下采样率分别为srL=srR=0.6,也就是说mL×nL=1075×1792,mR×nR=1075×1792.重建算法选用Van Den Berg 等人[12-13]提出来的SPGL1软件包,其可以用于求解大尺度图像的重建问题.
在图1中,图1(a)是原标准Lena测试图像,图1(b)是2个分离矩阵矩阵ΦL和ΦR皆是RNORM时对应的测量值,图1(c)是图1(b)出发使用重建算法恢复的估计图像.图1(d)是对应于RNRGM的测量值,图1(e)是RNRGM相应的重建结果.图1(f)是随机高斯矩阵(未归一化)对应的测量值,图1(g)是图1(f)中的测量值经过SVD处理后得到的新的测量值,图1(h)是从图1(g)出发得到的重建结果.注意,在最后一个RGM+SVD的重建实验中,经过SVD处理后,相应的测量矩阵和测量值都发生了变化,此处仅给出变化后的测量值.各重建图像的信噪比(signal-to-noise ratio, SNR)以及重建时间(time)如表1所示:
Table 1 The Comparison Results of SNR and Time of Image Reconstruction Using Different Separable Measurement Matrices
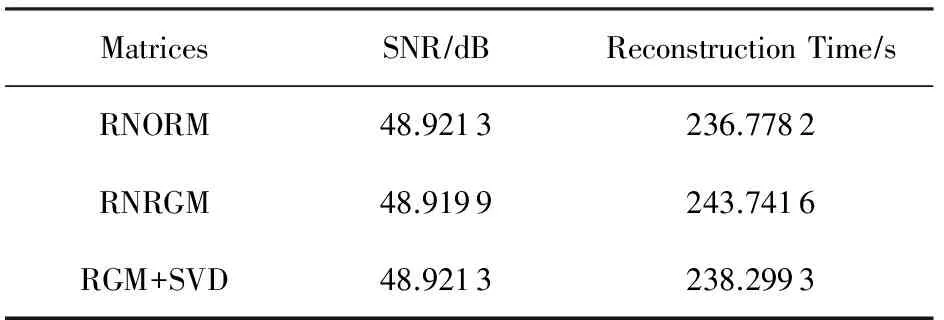
表1 不同可分离测量矩阵图像的重建信噪比和重建时间
从表1中的数据可以看出,3种矩阵的重建质量度量基本上是一样的,彼此差距很小.重建时间指标也类似.从理论上来说,RNORM应该具有最优的结果,重建结果的稳定性最有保证.这是因为正交矩阵具有最小的互相干因子,从而可以优化重建的性能.在最小的测量数目情形下,可以得到同样质量的重建图像.由于重建时间不是本文关注的重点,因此后续实验仅关注重建结果的SNR值.
3.2 实验2:不同下采样率重建实验
为进一步测试本文方法的有效性,实验2的目的是测试本文的方法在不同采样率下的重建性能表现.实验中选用3种不同的原型矩阵,即随机高斯矩阵(Gauss)、随机托普利兹矩阵(Toep)和随机循环矩阵(Circ),后2种矩阵的随机独立元素相比Gauss矩阵要少得多,可以显著降低测量矩阵的实现难度,是实际物理实现时必须考虑的一点,因此这里也拿来作为一种对比测试.
实验2中,单个分离测量矩阵的下采样率作为实验中的可变参数(左右保持相同的下采样率),其下采样率分别为srL=srR∈{0.5,0.6,0.7,0.8,0.9},总的下采样比率(sample rate, SR)β=srLsrR.每组相同参数重建实验分别运行100次,取其重建SNR的均值.测试图像选用标准Lena图像和Cameraman图像,图像尺寸一组为256×256,另一组为768×768,实验结果如图2所示:
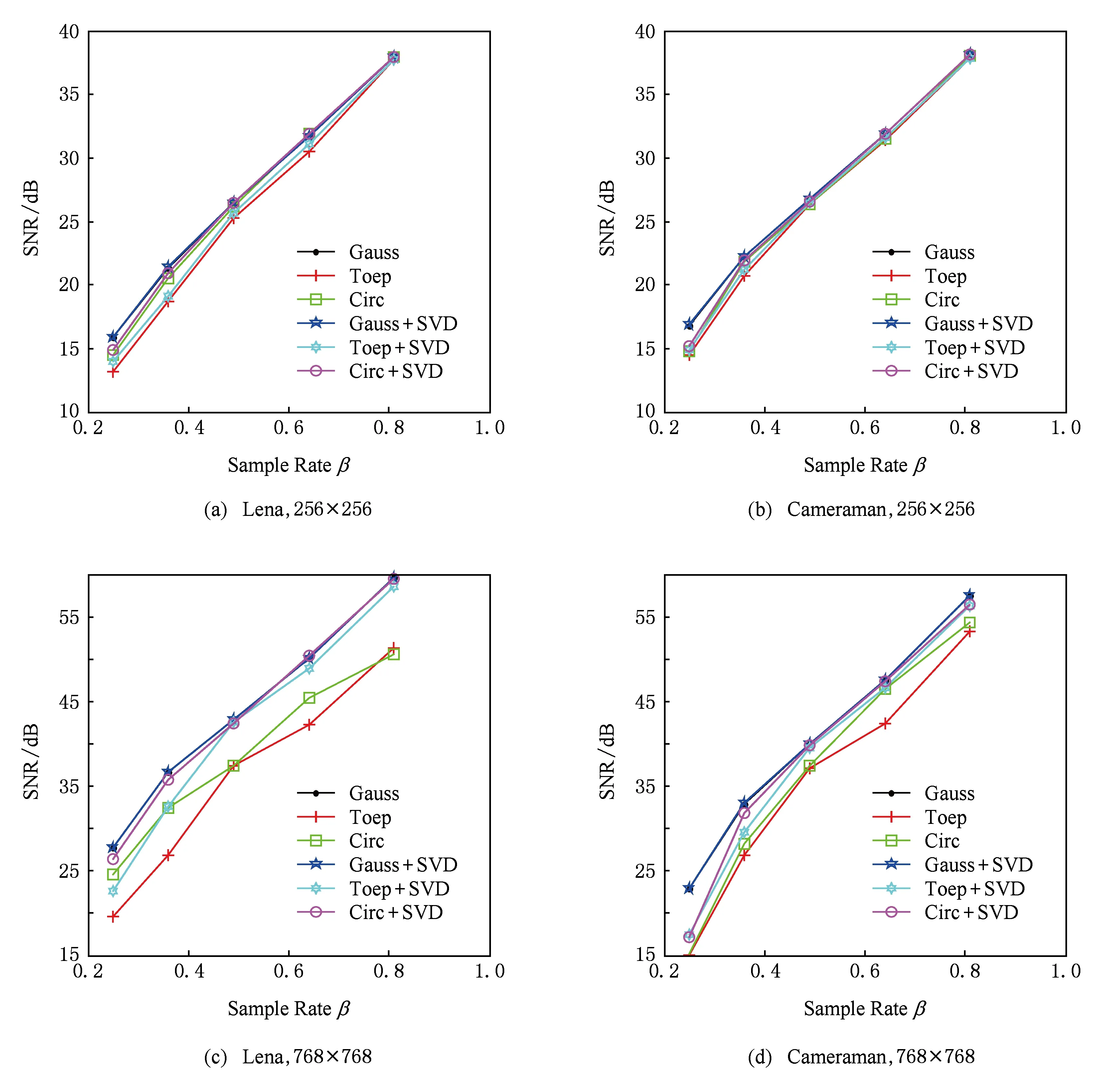
Fig. 2 Comparison of reconstruction experiments under different sampling rate.图2 不同下采样率下的对比重建实验
从图2可以看出,随着总采样率β的变大,所有矩阵的平均重建SNR都逐渐提高.该趋势也符合CS理论中的测量越多,测量值中所包含原图像信息越多的原则.另一方面,对于随机Gauss矩阵而言,在不同下采样因子的情形下,RNRGM和采用SVD之间的差别不大.
但是对随机托普利兹矩阵(Toep)和随机循环矩阵(Circ)矩阵而言,在较低分辨率(256×256)时,从图2(a)和图2(b)可以看到,加上SVD预处理步骤略优于未加的SVD的结果,实际差距非常小.这是因为在低分辨率情形下,SVD提供的优化性能有限,差别并不明显.但是,当分辨率变大(768×768)时,二者之间的差距开始非常显著,本文的方法对于确定性矩阵(Toep和Circ矩阵)而言,要远优于未加上SVD步骤的方法,其平均信噪比有显著的提高,表现出非常有吸引力的稳定性.
3.3 实验3:不同尺度的重建实验
设计第3组实验的目的是测试本文提出的方法在不同图像尺度情形下的重建结果.图像的基本尺寸是256×256,然后分别放大×1,×2,×3,×4,×5,×6,×7共7个级别.×4的意思就是图像的水平和垂直方向都被放大4倍,即1024×1024,其余以此类推.左右分离矩阵的下采样率分别为srL=srR=0.7,总下采样比率β=0.49.实验同样选取随机高斯矩阵(Gauss)、随机托普利兹矩阵(Toep)和随机循环矩阵(Circ)来作对比测试.测试图像选用标准Lena图像和Cameraman图像,每组实验独立运行100次,计算其平均SNR,测试曲线如图3所示:
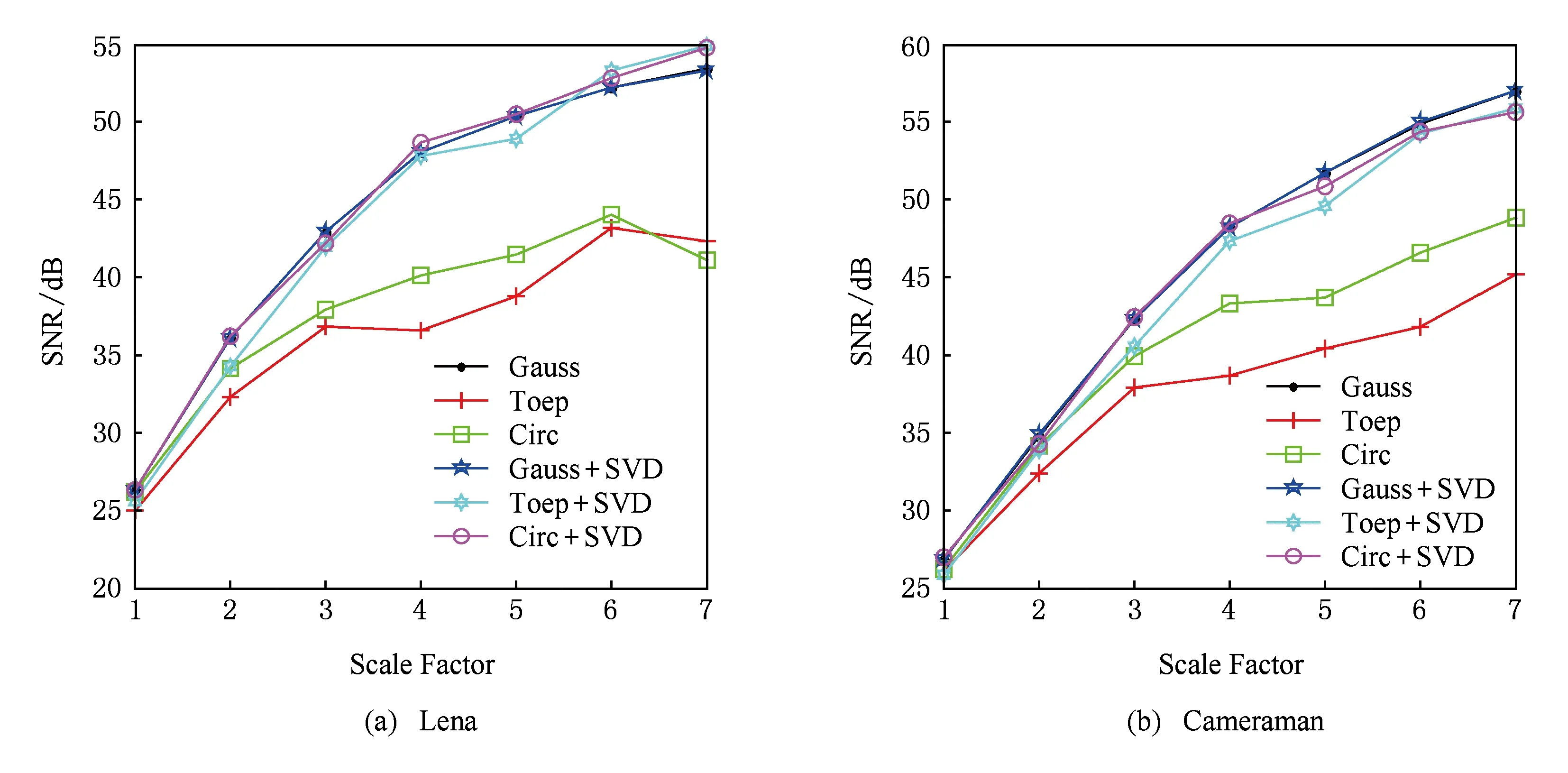
Fig. 3 Comparison of reconstruction experiments under different scale factors.图3 不同尺度下的对比重建实验
从图3可以看出,对随机高斯矩阵(Gauss)而言,不同图像尺寸下仍然保持了较好的平均重建SNR,总体趋势符合测量数目越多,包含信息越多的特点;但是随机托普利兹矩阵(Toep)和随机循环矩阵(Circ)无论是在Lena图像还是Cameraman图像上的测试结果都表现出非常明显的不稳定性.
这是由于这2类矩阵(Toep和Circ)独立元素的数目要远少于随机高斯矩阵:一方面,这带来了有利的一面是降低了测量矩阵的随机性,从而可以降低前端测量物理实现的难度与成本;但是另一方面,随机性的降低也导致有部分信息不能进一步地被成功提取出来以提高重建图像的细节信息,因此导致在大尺度情形下平均重建SNR的波动.图像尺寸越大,这一点也表现得越明显.随着图像尺寸的增大,采用本文的方法可以非常显著地提高重建信噪比,表现出非常优越的稳定性.
3.4 实验4:鲁棒性测试
实验4是用于鲁棒性测试的.其具体步骤是给原图像附加一定信噪比的噪声,然后按照SCS的方法进行测量与重建,统计其平均信噪比.测试图像选用Lena图像和Cameraman图像.图像的大小都是256×256像素,左右分离矩阵的下采样率分别为srL=srR=0.7.测试矩阵仍采用随机高斯矩阵(Gauss)、随机托普利兹矩阵(Toep)和随机循环矩阵(Circ).
输入图像的SNR(Input SNR)分别为10 dB,15 dB,20 dB,25 dB,30 dB,35 dB,40 dB.该噪声是通过Matlab中的Fn=awgn(F,snr,“measured”)命令附加上相应的随机高斯噪声.其中F表示原图像,snr表示给定的输入信噪比.由于随机噪声的不确定性,本实验中重新统计加噪声和未加噪声测量值之间的信噪比作为最终的输入信噪比.每组实验独立运行100次,计算其平均SNR,实验曲线如图4所示.
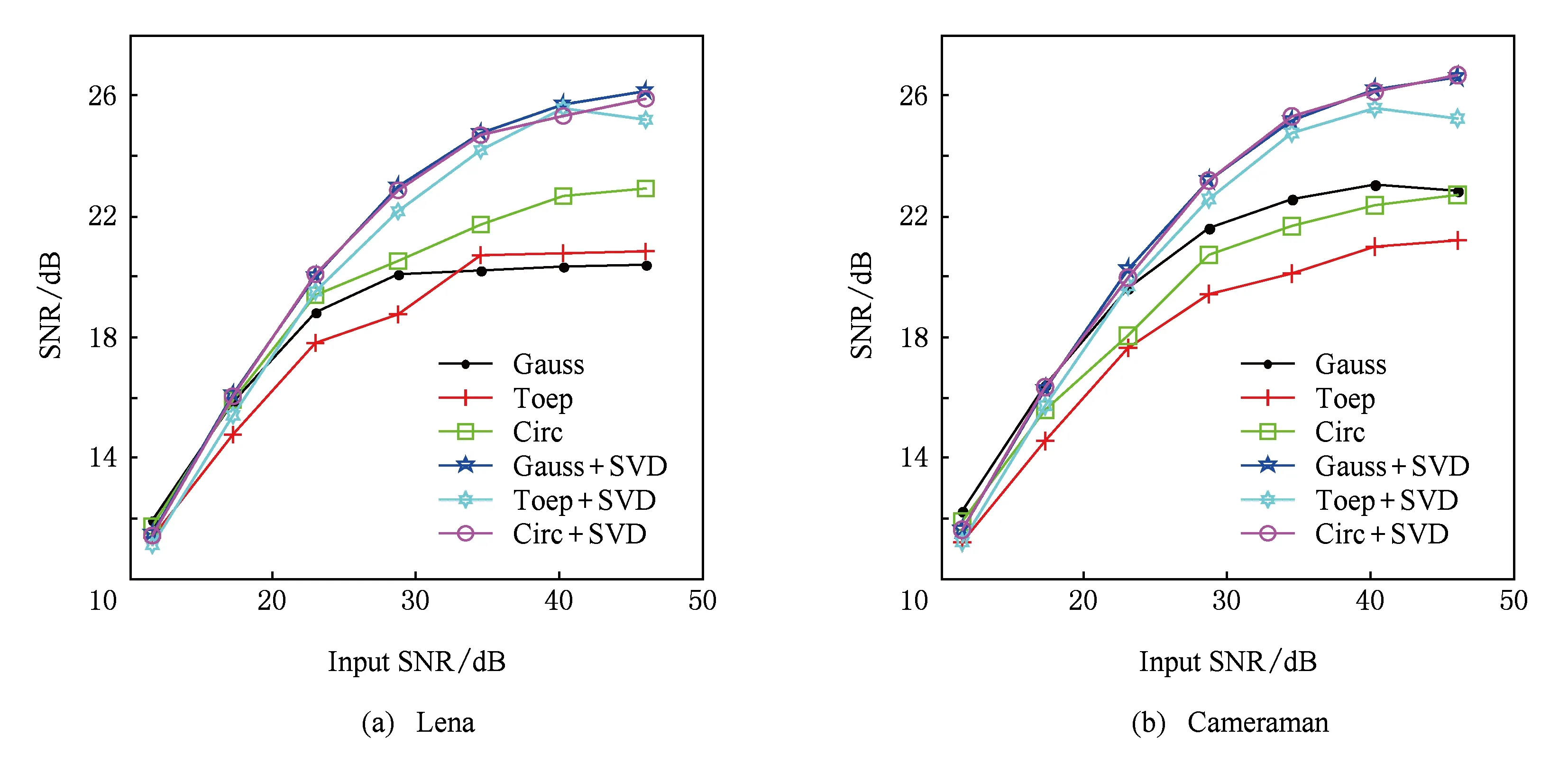
Fig. 4 Robustness testing experiment.图4 鲁棒性测试实验
从图4可以看出,随着输入SNR的提高,各测试矩阵的平均重建SNR也逐渐提高;但是,可以很明显地看出来,本文提出的方法有非常优越的稳定性,尤其是在较高输入SNR的情形下,可以非常充分地提取原图像的细节信息得到更高的重建信噪比.
4 结 论
本文提出一种基于SVD的可分离、可压缩传感方法,可以用于图像的分离可压缩传感与重建.其基本思想是采用SVD分解方法对左、右分离测量矩阵分别进行预处理,从而得到优化后的测量矩阵与测量值,其中改进后的测量矩阵是行正交的(行数小于列数).使用该方法可以有效地实现测量矩阵和重建矩阵的有效分离:在采集阶段,测量矩阵的设计方面更多地考虑其物理可实现的性质,如托普利兹矩阵或循环矩阵等;在图像重建阶段,更多地考虑优化重建矩阵的性能.一系列的数值测试结果表明本文方法的有效性,尤其是在独立元素较少的确定性测量矩阵(托普利兹和循环)的大尺度图像重建重建结果上更具有突出优势,表现出卓越的稳定性.
[1]Romberg J. Compressive sensing by random convolution[J]. SIAM Journal on Imaging Sciences, 2009, 2(4): 1098-1128
[2]Zhang Cheng, Zhang Fen, Shen Chuan, et al. Binary pure phase encoding compressive imaging in frequency domain [J]. Journal of Computer Research and Development, 2014, 51(9): 2070-2080 (in Chinese)(张成, 张芬, 沈川, 等. 频域二元纯相位编码压缩成像[J]. 计算机研究与发展, 2014, 51(9): 2070-2080)
[3]Candès E J, Wakin M B. An introduction to compressive sampling[J]. IEEE Trans on Signal Processing Magazine, 2008, 25(2): 21-30
[4]Rivenson Y, Stern A. Compressed imaging with a separable sensing operator[J]. IEEE Trans on Signal Processing Letters, 2009, 16(6): 449-452
[5]Rivenson Y, Stern A. Practical compressive sensing of large images[C/OL] //Proc of the 16th Int Conf on Digital Signal Processing. 2009: 1-8 [2013-10-21]. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnu mber=5201205
[6]August Y, Vachman C, Rivenson Y, et al. Compressive hyperspectral imaging by random separable projections in both the spatial and the spectral domains[J]. Applied Optics, 2013, 52(10): D46-D54
[7]Donoho D. Compressed sensing[J]. IEEE Trans on Information Theory, 2006, 52(4), 1289-1306
[8]Candès E, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Trans on Information Theory, 2006, 52(2): 489-509
[9]Goodman J W. Introduction to Fourier Optics[M]. Chicago: Roberts and Company Publishers, 2005
[10]Zhang Cheng, Yang Hairong, Wei Sui. Compressive double-lens imaging using circulant-toeplitz-block phase mask[J]. Acta Optica Sinica, 2011, 31(8): 0811001 (in Chinese)(张成, 杨海蓉, 韦穗. 循环-托普利兹块相位掩模可压缩双透镜成像[J]. 光学学报, 2011, 31(8): 0811001)
[11]Baraniuk R, Choi H, Neelamani R, et al. Rice wavelet toolbox[OL]. [2012-10-21]. http://dsp.rice.edu/software/rice-wavelet-toolbox
[12]van den Berg E, Friedlander M P. Probing the Pareto frontier for basis pursuit solutions[J]. SIAM Journal on Scientific Computing, 2008, 31(2): 890-912

[13]van den Berg E, Friedlander M P. Sparse optimization with least-squares constraints[J]. SIAM Journal on Optimization, 2011, 21(4): 1201-1229Zhang Cheng, born in 1984. Received his PhD degree in the School of Electronics and Information Engineering from Anhui University in 2012. Lecturer in the School of Electronics and Information Engineering, Anhui University. His main research interests include compressed sensing, matrix completion, optical imaging and phase retrieval.

Wang Dong, born in 1993. Master candidate in the School of Electronics and Information Engineering, Anhui University. His main research interests include compressive holography and 3D imaging (729989855@qq.com).

Shen Chuan, born in 1986. Received his PhD degree in the School of Electronics and Information Engineering from Anhui University in 2015. Lecturer in the School of Electronics and Information Engineering, Anhui University. His main research interests include holographic imaging and signal processing (shenchuan2502@163.com).

Cheng Hong, born in 1981. Received her PhD degree in the School of Electronics and Information Engineering from Anhui University in 2012. Associate professor in the School of Electronics and Information Engineering, Anhui University. Her main research interests include transport of intensity equation(TIE).

Chen Lan, born in 1976. PhD candidate in the School of Electronic and Optical Engineering, Nanjing University of Science and Technology. Lecturer in the School of Electronics and Information Engineering, Anhui University. Her main research interests include compressive sensing.

Wei Sui, born in 1946. Graduated from Nanjing Industrial College (now South-east University) in 1970. Professor in Anhui University and member of doctoral faculty. Her main research interests include computer vision and imaging & display.
Separable Compressive Imaging Method Based on Singular Value Decomposition
Zhang Cheng1,2, Wang Dong1, Shen Chuan1, Cheng Hong1, Chen Lan1, and Wei Sui1
1(Key Laboratory of Intelligent Computing & Signal Processing (Anhui University), Ministry of Education, Hefei 230039)2(KeyLaboratoryofModernImagingandDisplayingTechnologyofAnhuiProvince(AnhuiUniversity),Hefei230039)
When facing the compressive imaging problem that the measurement matrix has too large dimension, separable compressive sensing (SCS) can effectively achieve this problem at a cost of a certain percentage of additional measurements. However, the both separable measurement matrices in existing separable compressive sensing method should be row-normalized orthogonal random matrix, which limits its application significantly. In this paper, the method of singular value decomposition (SVD) is introduced into separable compressive sensing measurement process, which can effectively achieve the separation of measurement matrix and reconstruction matrix: the design of the measurement matrix in sensing stage is more to consider the physical properties for easy implementations, such as the deterministic structure of Toeplitz or Circulant matrices and etc; in the reconstruction stage, it is more to consider the optimization of reconstruction matrix. Through the introduction of singular value decomposition method to optimize the measurement matrix in reconstruction stage, the reconstruction performance can be effectively facilitated, especially for Toeplitz and Circulant matrix in large-scale image compressive reconstruction. Numerical results demonstrate the validity of our proposed method.
compressive imaging (CI); separable compressive sensing (SCS); separable sensing matrix; singular value decomposition (SVD); deterministic matrices
2015-06-01;
2015-12-16
国家自然科学基金项目(U1201255,61301296,61377006,61501001,61605002);安徽省自然科学基金项目(1608085QF161);安徽省高等学校自然科学研究项目(KJ2015A114,KJ2016A029) The work was supported by the National Natural Science Foundation of China (U1201255, 61301296, 61377006,61501001, 61605002), the Natural Science Foundation of Anhui Province (1608085QF161), and the Natural Science Research Project of the Colleges and Universities of Anhui Province (KJ2015A114, KJ2016A029).
韦穗(swei@ahu.edu.cn)
TP391; TN911.7
