分簇无线传感器网络级联失效抗毁性研究
2016-12-22符修文李文锋
符修文 李文锋 段 莹
1(河南科技大学车辆与交通工程学院 河南洛阳 471003)2(武汉理工大学物流工程学院 武汉 430063)(fuxiuwen1987@163.com)
分簇无线传感器网络级联失效抗毁性研究
符修文1李文锋2段 莹2
1(河南科技大学车辆与交通工程学院 河南洛阳 471003)2(武汉理工大学物流工程学院 武汉 430063)(fuxiuwen1987@163.com)
无线传感器网络(wireless sensor network, WSN)级联失效对象多以对等平面结构为对象,但在现实情形中,多数无线传感器网络采用典型分簇结构进行数据采集与传递.因此,考虑分簇传感器网络中节点所拥有连接的异质性,引入感知负载与中继负载等概念,建立分簇级联失效模型,探讨分簇无标度网络和分簇随机网络的级联失效抗毁性能与模型关键参数之间的关联特征,并研究如何选取合适的簇头节点扩充容量达到抑制网络级联失效规模的目的.数值模拟与理论分析结果表明:分配系数A与网络级联失效性能正相关,簇头比例p与网络抗毁性能负相关.当调节参数α=1时,网络级联失效抗毁性能达到最优;当调节参数α<1时,选取簇-簇连接度较小的簇头节点扩充容量能够更为有效地提升网络级联失效抗毁性能;当调节参数α>1时,选取簇-簇连接度较大的簇头节点扩充容量抗毁性能提升效果更为明显;当调节参数α=1时,网络级联失效规模与簇头选取策略无关.
无线传感器网络;级联失效;分簇结构;抗毁性;无标度拓扑;随机拓扑
布置在恶意环境中的无线传感器网络(wireless sensor network, WSN)常会因为人为入侵或自然灾害等外部原因导致节点失效.除此之外,传感器节点通常采用移动电源供电,常因成本受限或部署环境恶劣等原因,导致节点能量耗尽或软硬件故障而无法正常工作.失效节点会使得原本连通的网络拓扑分割,从而大大降低网络的连通度与覆盖度,甚至导致全局网络瘫痪[1-4].由于规模巨大、资源受限、传递时延与有向传输等内在因素产生的非线性网络行为难以预测,研究WSN抗毁性行为对解决WSN规模应用瓶颈具有重要的理论价值.
现有WSN抗毁性研究多从静态角度,研究移除点或边对网络拓扑连通性与可用性的影响,并未考虑网络的动态性过程.但在现实WSN中,网络拓扑结构的改变将会造成网络数据流的重新分配,导致网络通信负载动态变化.受制于硬件成本,传感器节点往往链路带宽受限,当实时通信负载高于节点额定载荷,将导致节点因链路堵塞而引发过载失效.WSN作为典型的以数据为中心的任务驱动型网络,节点失效的发生将导致网络负载再分配,进而可能造成其他节点因过载而失效,从而引发新一轮的负载分配,并最终导致大规模网络级联失效的发生.因此,级联失效普遍存在于现实WSN中,是影响WSN抗毁性能的主要因素[5-7].
当前针对网络级联失效问题,有众多学者展开研究.Motter等人[8]最早提出负载-容量模型,该模型定义每个节点均拥有一定容量并承担相关负载.当节点失效行为发生,则该节点所承担负载按照预设规则转移至网络中剩余其他节点.而其他节点也将可能因负载超出自身容量而导致失效,并引发新一轮的负载转移.后续诸如CASACADE模型[9]、OPA模型[10]等均是在负载-容量模型基础之上发展而来.现实世界中,不同类型网络所对应级联失效情形各不相同.研究表明:输配电网络[11]、物流保障网络[12]、交通网络[13]及因特网[14]等均具有明显的级联失效特征且彼此间具有明显差异.在归纳总结基础上,现实网络通常被划分为:随机网络、小世界网络与无标度网络.因而,有众多学者针对这3种广义网络类型展开级联失效抗毁性研究.WSN作为数据驱动型的新兴信息网络也得到越来越多学者的重视.Liu等人[15]基于介数定义节点负载,建立WSN级联失效模型,并在此基础上提出级联失效抗毁性测度.由于节点介数计算依赖于全网最短路径的获取,这就要求节点必须拥有全局网络路由信息,但对于多数WSN而言,全局信息的获取十分困难;Yin等人[16]根据节点可变负载与恒定容量等特点,针对WSN无标度拓扑展开研究,得到度分布指数和幂律系数与WSN容错性能正相关这一结论;李雅倩等人[5]则在此研究基础上,借助概率母函数法求解WSN无标度拓扑级联失效的临界负载值.尽管现有WSN级联失效研究取得一定成果,但所针对WSN对象均为对等平面结构,即网络内所有节点角色、功能均完全一致.然而在现实情形中,由于受网络规模和以能耗与延时为代表的服务质量要求,多数WSN均采用典型分簇结构进行数据采集与传递.现有WSN级联失效研究对于此类普遍情形并不适用.
基于上述考虑,本文针对真实情形下WSN普遍存在的分簇结构,引入中继负载与感知负载等概念,建立分簇WSN级联失效模型.基于网络演化分别提出分簇WSN的无标度与随机拓扑演化模型.在此基础上,通过理论推导与仿真分析相结合的方式,验证级联失效模型中各关键参数对所提分簇WSN模型级联失效抗毁性能的影响,获得了节点随机失效情形下分簇WSN大规模级联失效临界负载值与网络分簇概率、负载和容量参数之间的关联特征.除此之外,研究如何选取合适的簇头节点扩充容量达到抑制网络级联失效规模的目的.通过以上研究为后期构建具有较强级联失效抗毁性能的分簇WSN拓扑提供了理论参考.
1 分簇WSN级联失效模型
1.1 负载-容量模型
分簇WSN通常由簇头节点与簇内成员节点构成.簇内成员节点负责采集所覆盖区域内的环境信息,将数据汇聚至所属簇头节点.簇头节点负责簇内信息的集中处理与发送,除此之外,还需承担来自其他簇头节点中继数据的转发任务.由于节点负载通常与节点自身度存在明显关联[5-6,16-17],且在分簇WSN中,节点所拥有连接具有明显的异质性,定义网络中任意节点j的初始负载Lj为
(1)
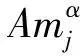
在实际网络中,由于每个节点处理负载的能力通常受布设成本等因素制约,节点间容量并不相同.在确定节点的容量时通常遵循“按需定容”原则[5-13].所以,一般认为节点的负载容量Cj与其初始负载Lj成正比,即:
(2)
其中,T(T≥1)为网络容忍系数,显然T值越大,节点处理额外负载的能力越强.
1.2 负载分配策略
在文献[5,15]中,当WSN中任意节点j发生失效,它的自身负载将平均分配至与其相邻的其他节点.正如1.1节所述,对于传感器节点而言,负载分为感知负载与中继负载.当节点失效行为发生,节点因无法感知周边环境,没有感知数据产出.它的感知负载也随之消失,因而无法转移至其他节点.但对于中继负载,当节点失效发生,原本需要通过它转发的数据量需要重新路由,从而产生新一轮的负载分配.但该过程的负载重新分配仅限于中继负载.因而,以往文献中,有关全部负载均全部用于重分配过程的策略设计与真实情形相比并不准确.除此之外,当节点确定有负载需要重新分配,则与之直接相连的节点中,度数越高的节点有更高的概率承担更多的负载.因而,以往文献中有关负载的平均分配策略具有明显的局限性.
因此,针对上述不足,本节针对分簇WSN给出4项负载分配策略:
1) 初始状态.WSN中任意节点负载均小于其容量,网络处于正常运行状态.当有节点发生失效时,其中继负载将重新分配到与其相邻的节点,引起网络中负载重新分配.该过程又可能导致新的节点失效行为发生,从而引发新一轮的负载重分配.该级联过程持续到没有新的失效节点出现时才完全停止.
2) 当簇内成员节点发生失效,因自身感知任务无法继续进行,所以无法向所属簇头节点发送数据,自身不承担中继转发任务,无中继负载需要分配.因此,并不会引发负载重分配过程,则级联失效过程不会发生.
3) 当簇头节点发生失效,因自身无法进行中继传输,则所辖簇内成员节点因无法借助簇头节点向簇外传递数据也随之失效.原有途经失效簇头节点的中继数据根据局域择优分配原则分配至周边与之相连的其他簇头节点.
4) 假定网络中簇头节点j失效,则与之直接相连的簇头节点i获得的负载Δij为
(3)
其中,Ωj为簇头节点j所拥有邻居簇头节点集合.假设负载分配完成时刻为t,则此时簇头节点i所承担负载为Li(t)=Li(t-1)+Δij.若Li(t)>Ci,则节点i在时刻t+1陷入失效状态,并引发新一轮的负载分配.不难理解,依照本文所提分配策略,若邻居簇头节点拥有的簇-簇连接数越多,则所获得的负载分配比例越高.正如1.1节所述,在分簇WSN中,一个簇头节点所连接的簇头节点数量表明了该节点在网络数据转发任务中的重要性程度.因而,本文给出负载分配策略合理有效.
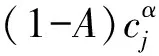
(4)
当中继负载重分配过程完成后,若簇头节点a,b,c中有节点因新增负载使得节点实时载荷超过额定容量,即存在Li(t+1)>Ci,i={a,b,c},则产生新的簇头节点失效,新增失效簇头节点将自身负载按策略重分配至仍可正常工作的邻居簇头节点.该过程一直重复至网络中剩余簇头节点实时负载均未超过其自身容量为止.

Fig. 1 Local allocation strategy of clustering WSN.图1 分簇WSN局域分簇分配策略
1.3 级联失效抗毁性测度
根据负载分配策略,当簇内成员节点发生失效后,并不会引发级联失效.因此,本文重点研究对象为移除簇头节点所引发的级联失效对网络的破坏程度.为了量化网络被破坏的程度,首先给出失效节点的归一化指标.从初始网络中移除一个簇头节点j,并计算因其所产生的失效规模Sj(级联失效过程完全停止后,失效节点的累计和),然后依次对网络中的每个簇头节点进行移除并计算其失效规模,再取所有簇头节点失效规模之和,作归一化处理,得到网络级联失效规模S:
(5)
其中,C为网络中所有簇头所组成的集合,|C|为簇头节点数量,N为节点总数.显然,当S≈0时,网络可用节点数量在级联失效发生前后几乎不发生改变,具有很强的级联失效抗毁性能;反之,当S≈1时,说明网络中任意一个节点的失效都将导致网络因级联失效而陷入瘫痪.正如文献[17]所述,对于级联失效,比起关注级联失效对网络的破坏程度,人们更关心网络应对级联失效所能承载的极限.由分簇WSN级联失效的负载-容量模型与负载分配策略可知,容忍系数T越大,则网络承载级联失效的能力越强.因此,必然存在一个临界值Tc,当T≥Tc时,任意节点的移除都不会导致级联失效的发生且网络构造成本最低.不难理解,Tc即为网络为避免级联失效所应具备容忍能力T的最小值.显然,Tc值越小,网络应对级联失效的抗毁性能越强.
2 分簇WSN演化模型
由于网络拓扑结构对网络动力学特征行为有着至关重要的影响,本文选取2种典型WSN分簇拓扑来研究不同网络拓扑应对级联失效抗毁性能的差异.
2.1 分簇WSN无标度演化模型
分簇WSN无标度演化模型具体生成步骤为:
1) 初始化.开始给定m0个簇头节点与e0条边,为保证网络中不出现孤立节点,各个簇头节点至少存在一条边与其他簇头节点相连.
2) 择优增长连接.在每个单位时间步增加一个新节点,则该节点成为簇头节点的概率为p,并连接到网络中一个已经存在的簇头节点上.簇头节点j依照择优概率Π(i→j)与新入节点i建立连接,择优概率Π(i→j)与被选择簇头节点j的度数kj成正比,Π(i→j)表达示为
(6)
其中,N(t)为在当前时刻t网络所拥有簇头节点数量.
2.2 分簇WSN随机演化模型
分簇WSN随机演化模型具体生成步骤为:
1) 初始化.开始给定m0个簇头节点与e0条边.为保证网络中不出现孤立节点,各个簇头节点至少存在一条边与其他簇头节点相连.
2) 择优增长连接.在每个单位时间步增加一个新节点,则该节点成为簇头节点的概率为p,并随机连接到一个网络中已经存在的簇头节点上.则簇头节点j被选择连接概率为
Π(i→j)=1N(t).
(7)
按照上述规则经过一定时间演化,2个模型均可得时刻t时网络拥有节点总数S(t)=m0+t,簇头节点数量N(t)=m0+pt.显然,当t→∞时,S(t)≈t,N(t)≈pt.
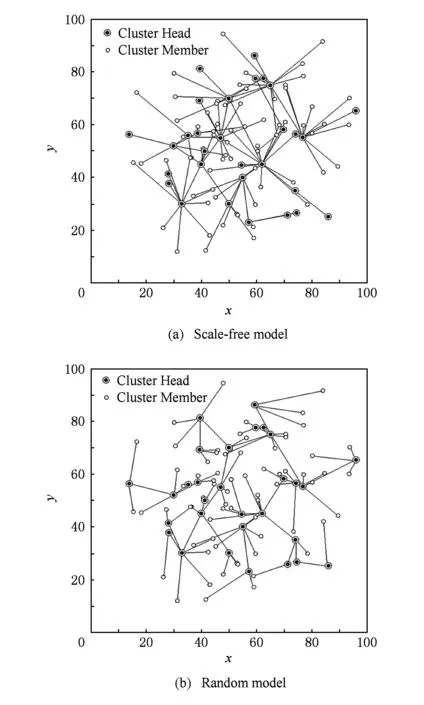
Fig. 2 Evolution model of clustering WSN.图2 分簇WSN演化模型
图2为初始网络与新加入节点位置均为一致,依照参数设定:簇头比例p=0.2,网络规模N=100所生成网络拓扑情形,此时节点平均度k=2.如图2(a)所示,在所得分簇WSN无标度拓扑中,绝大多数簇头节点度数为1,但少数簇头节点占用了网络中绝大多数连接,最高簇头节点度数可达11,具有明显的无标度特征.如图2(b)所示,分簇WSN随机拓扑度分布较无标度拓扑匀质性明显增强,网络中绝大多数簇头节点度数均为3~5,符合随机网络特征.
图3为将节点规模扩大至500后在双对数坐标系下所提分簇WSN无标度拓扑与随机拓扑的网络度分布情形.分簇WSN无标度拓扑度分布具备典型的幂律分布特征,对度分布曲线进行拟合,可得无标度拓扑服从幂律分布P(k)=1.6k-2.7.分簇WSN随机拓扑服从典型的指数分布,拟合后结果为随机拓扑服从指数分布P(k)=exp(-3.1k).为更准确验证所提2种网络演化模型的度分布特征,随后将对其度分布做进一步理论推导与分析.
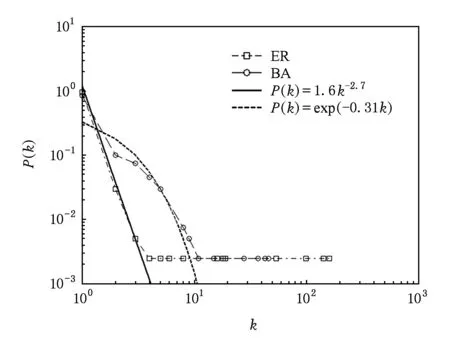
Fig. 3 Degree distribution of clustering WSN.图3 分簇WSN度分布
3 仿真分析
本节主要探讨级联失效模型和拓扑构造所涉及的关键参数(分配系数A、调节参数α、簇头比例p、容忍系数T)对网络级联失效抗毁性能的影响以及如何选取合适的簇头节点扩充容量抑制级联失效规模.
在仿真过程中,设定网络规模为400,且其他参数设置完全一致.仿真数值均为20次生成全新网络后获得的平均结果.根据网络演化机制,每单位时刻,2种网络模型均新增1个节点,且仅与网络内1个已有簇头节点相连.因此,最终所得2种网络拓扑节点总数、簇头节点数、边数及节点平均度在概率条件下将会完全一致.
3.1 模型关键参数对网络级联失效抗毁性能影响
图4为不同参数α取值时,容忍系数T与所引发级联失效规模S之间的关联.由图4不难发现,参数α的取值对网络级联失效抗毁性能有着重要影响.当α=1时,网络抗毁性能最优,此时,对于分簇无标度网络,关键阈值Tc=1.08,即当T>Tc=1.08时,网络对级联失效完全免疫.对于分簇随机网络,抗毁性能稍弱,关键阈值Tc=1.14.对于随机网络模型,有关S的性能曲线表现出明显的阶跃特征.这是由于α值越小,初始网络中度数较大节点与度数较小节点间的负载差异性也越不明显,从而降低整个网络系统对T值变化的响应度.仅当T达到某个局部阶跃值时,网络才会在局部范围出现节点崩塌现象.根据图4所示,当节点负载与自身度呈线性关系时(α=1),网络抗毁性能最优,这为网络抵御级联失效提供有益参考.后续仿真实验均选取α=1进行对比分析.
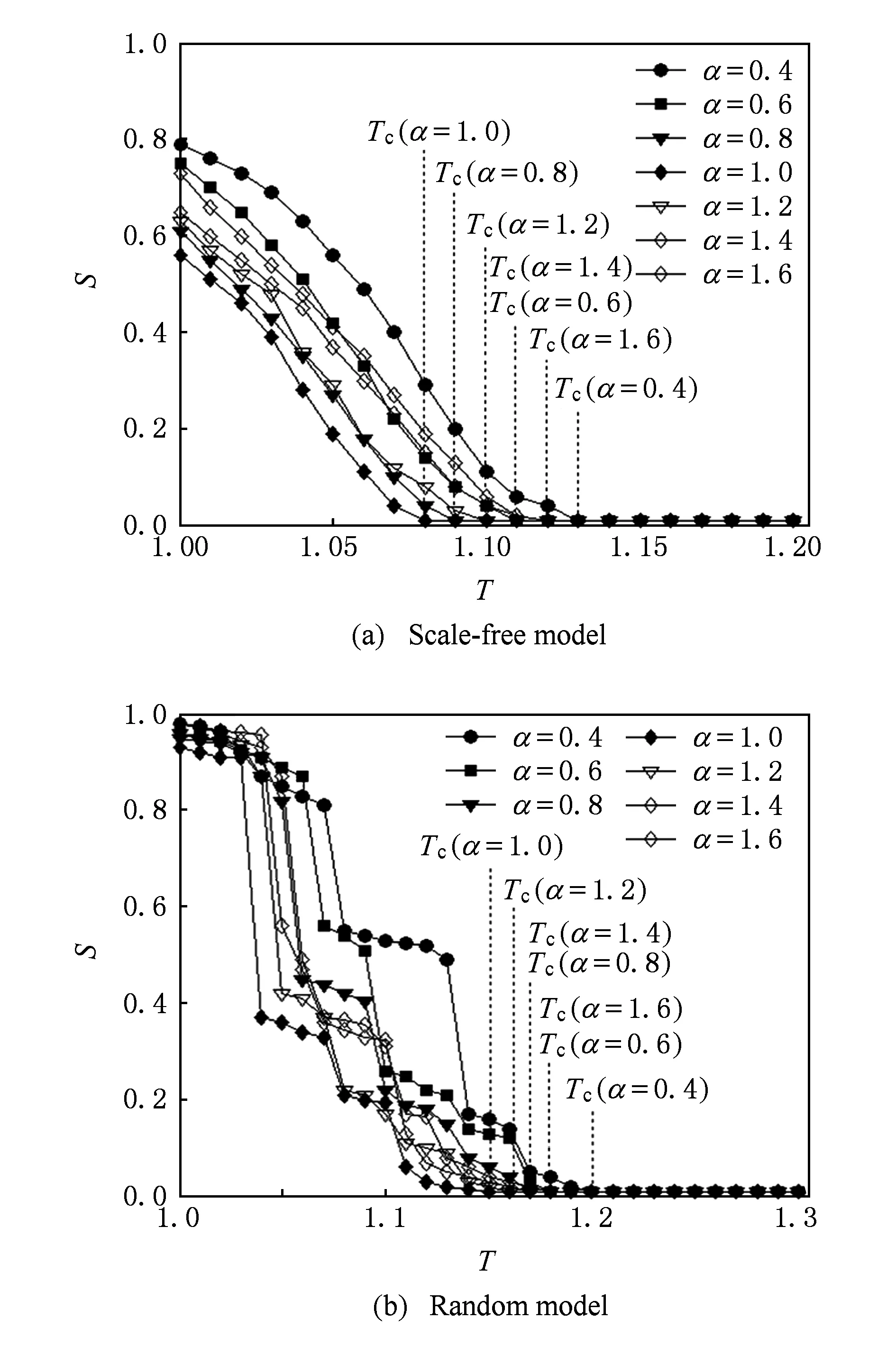
Fig. 4 Relation of α,T and S in two models (p=0.3,A=0.5).图4 2种网络模型中α,T与S关系(p=0.3,A=0.5)
如图5所示,分配系数A取值的上升将能够有效提升网络的级联失效抗毁性能.举例说明,对于无标度网络分簇模型,当A=0.3时,关键阈值Tc=1.14;当A上升至0.7,关键阈值Tc则下降至1.04.根据负载分配策略,对于簇头节点,当节点失效后,仅自身所承担的中继负载参与负载重分配过程.因此,A值的上升意味着网络中可供分配的中继负载数据量份额下降,而此时网络容量并没有因A值的变化而发生明显下降,从而使网络抵御级联失效的能力得到提升.这就告诉网络建设者在构造网络过程中,为提升网络抗毁性能,应尽可能减少因多跳转发所带来的数据增量.
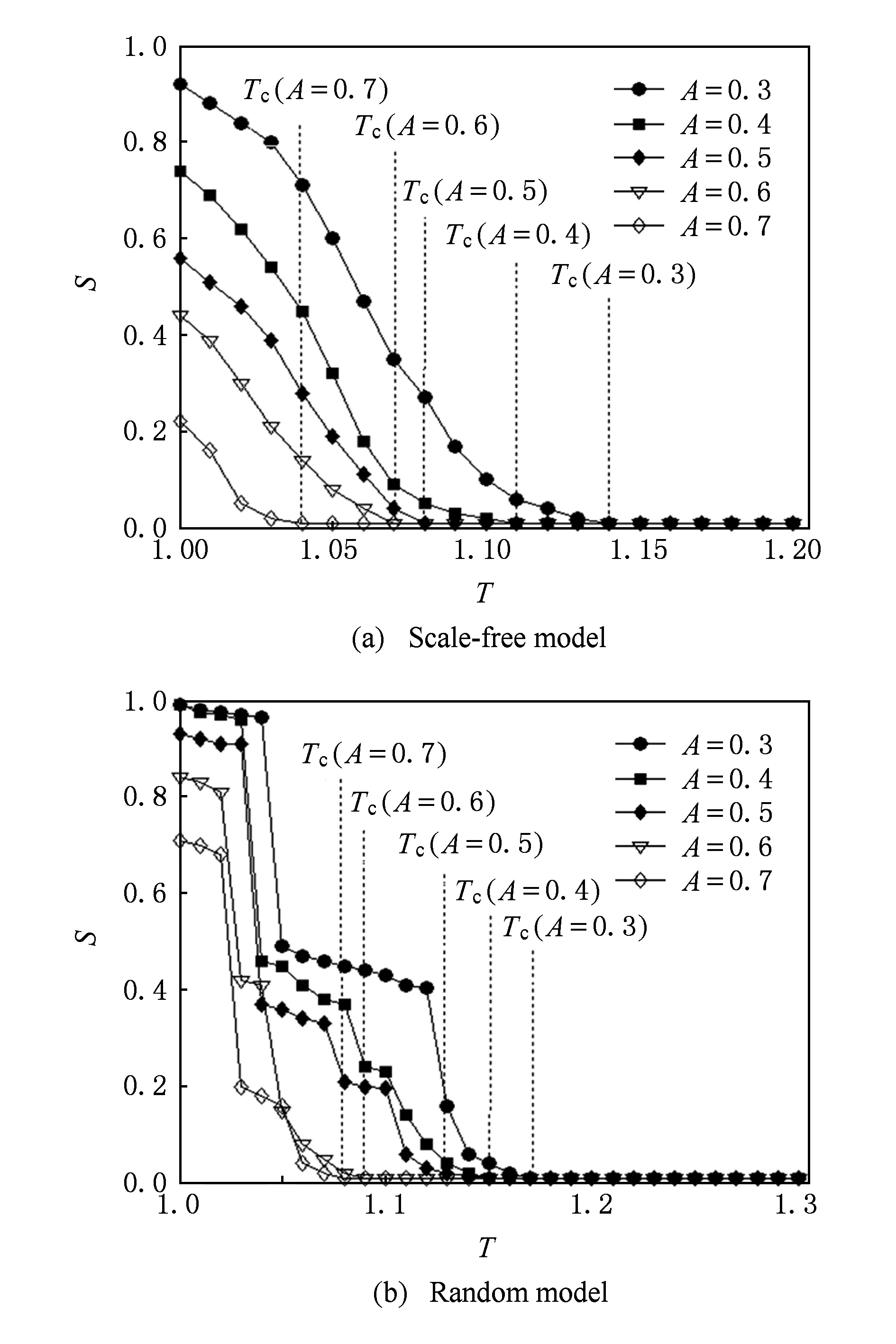
Fig. 5 Relation of A,T and S in two models (p=0.3,α=1).图5 2种网络模型中A,T与S关系(p=0.3,α=1)
如图6所示,随着簇头比例p取值的上升,网络级联失效抗毁性能也随之下降.p值的上升意味着单个簇头节点将可能拥有更多的邻居簇头节点.根据负载-容量模型,簇头节点中继流量与邻居簇头节点数量正相关,使得网络中可供重分配的中继负载数据量将随着p值的上升而增加,进而导致网络中簇头节点面临更大的容量过载风险.因此,为优化网络抗毁性能,应合理控制网络中簇头节点规模,减少数据从采集端到Sink节点的中继转发环节.

Fig. 6 Relation of p,T and S in two models (A=0.5,α=1).图6 2种网络模型中p,T与S关系(A=0.5,α=1)
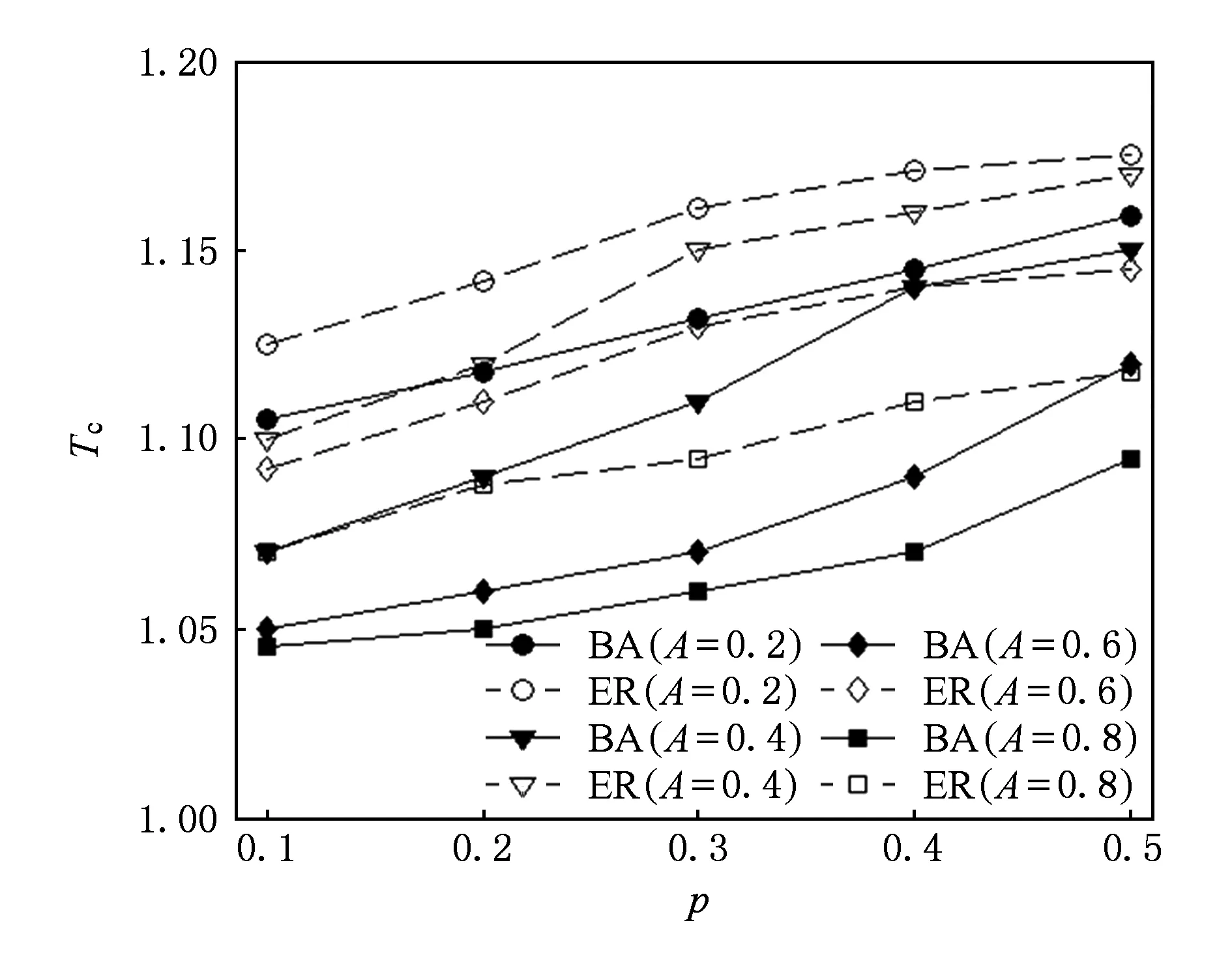
Fig. 7 Relation of p,A and Tc in two models (α=1).图7 2种网络模型中p,A与Tc关系(α=1)
图7为在无标度模型与随机模型中p,A与Tc的关系示意图.为方便表示,在图7中无标度模型简写为BA,随机模型简写为ER.不难发现,在相同参数设置条件下,无标度网络的关键阈值Tc均明显小于随机网络,进而得到无标度网络应对级联失效抗毁性能优于随机网络这一结论.这是由于无标度网络中绝大多数节点度数较小,移除这一类节点并不能触发级联失效过程.但值得注意的是,尽管无标度网络触发级联失效的难度明显高于随机网络,但并不意味着级联失效过程对于无标度网络的影响小于随机网络.综合图4至图6分析,当级联失效过程发生,无标度网络级联失效规模S高于随机网络.这是由于在无标度网络中,一旦级联失效过程发生,就通常意味着网络中的高度数中心节点陷入失效,从而极易导致与之相连的节点相继陷入失效状态,进而引发大范围网络失效.
3.2 容量扩充策略分析
从分簇WSN级联失效过程可以发现,当网络中有簇头节点失效行为发生,则失效簇头节点所承担的中继负载将根据邻居簇头节点所拥有簇-簇连接数按比例进行重新分配.若邻居簇头节点容量能够满足失效簇头节点中继负载转移的需求,则网络级联失效终止.因此,设计合适策略选择网络中部分关键节点进行扩容,可以达到降低网络级联失效规模的目的.
与无区别提升全网节点容量相比,引入针对性策略选择关键节点扩充容量,可在提升网络应对级联失效抗毁性能的同时降低网络硬件投入成本.因此,在本节初步探讨如何设计合理的容量扩充策略控制网络级联失效规模.3种面向簇头节点的容量扩充选择策略为
1) 度大扩容策略(higher-degree scheme, HDS).依照所拥有的邻居簇头节点数量从高至低,从全网簇头节点中选取比例为G的簇头节点进行容量扩充,使扩充后的容量较初始容量提升10%.
2) 度小扩容策略(lower-degree scheme, LDS).依照所拥有的邻居簇头节点数量从低至高,从全网簇头节点中选取比例为G的簇头节点进行容量扩充,使扩充后的容量较初始容量提升10%.
3) 随机扩容策略(random scheme, RS).从全网簇头节点中随机选取比例为G的簇头节点进行容量扩充,使扩充后的容量较初始容量提升10%.
为更好对比3种扩容策略对网络级联失效抗毁性能的影响,分别考虑α<1,α=1,α>1这3种情形,结合3.1节关键参数(分配系数A、调节参数α、簇头比例p、容忍系数T)对网络级联失效抗毁性能影响的仿真分析,不难得到分配系数A、簇头比例p、容忍系数T与网络抗毁性能均呈明显的单调相关.而调节参数α与网络抗毁性能具有典型的单峰函数关联特征,仅当α=1时,网络抗毁性能最优.因其特殊性,将调节参数α分为3个区间,重点分析不同α区间下所提3种扩容策略的效用.

Fig. 8 Comparison of lifting effects of various capacity-enlarging schemes (A=0.5,p=0.3).图8 不同扩容策略对网络提升效果对比(A=0.5,p=0.3)
如图8所示,针对α<1,α=1,α>1这3种情形,3种扩容策略对网络级联失效抗毁性能的提升效果各不相同.针对α<1情形,设置α=0.6,无论对于无标度网络或是随机网络,度小扩容策略的网络抗毁性能提升效果最优;针对α=1情形,3种扩容策略效果相近;针对α>1情形,设置α=1.4,相比其他2种扩容策略,度大扩容策略能够更为有效地抑制网络级联失效行为的发生.通过归纳不难得到:针对α<1情形,网络中度数较小的簇头节点失效更容易触发级联失效过程,因而度小扩容策略效果更为明显;相反,对于α>1情形,网络中度数较大的节点可被视为影响网络级联失效抗毁性能的主要短板,因而度大扩容策略效果更优;而针对α=1情形,网络级联失效抗毁性能的高低对于选取哪一类簇头节点进行扩容并不敏感.后续理论分析针对不同扩容策略对网络抗毁性能的提升效果做进一步阐述.
4 理论分析
本节首先对所提的2种网络演化模型进行理论分析,以求得精确的理论度分布.并在此基础上,理论验证所提级联失效模型中各关键参数对所提分簇WSN模型级联失效性能的影响和不同扩容策略对网络级联失效抗毁性能的提升效用.
4.1 网络模型度分布
度分布P(k)表示网络中任意节点度数为k的概率,是评估网络拓扑类型最直观的参数.在本文模型中,普通簇内成员节点仅可与簇头节点相连,因此该类节点度k始终为1.而对于簇头节点i而言,伴随网络演化时刻t,ki(t)动态增长.因此,基于平均场理论[17]分别求解分簇WSN无标度拓扑与随机拓扑度分布.
1) 分簇WSN无标度演化模型度分布
由演化机制易得,ki(t)满足动力学方程:
(8)
考虑网络长时间演化情形,可得:

(9)
k(t)
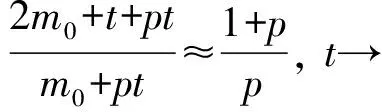
(10)
将式(9)与式(10)带入式(8),则式(8)可化简为
(11)
对式(11)做等价变换:
(12)
式(12)为ki(t)随t变化的微分方程,由网络生成规则可知:节点i初加入网络时度数为1,可得初始条件ki(ti)=1,对其进行求解,可得特解:
(13)
则簇头节点i在时刻t满足ki(t) (14) 本文仅考虑以最常见的等时间间隔方式添加节点,因此,ti具有等概率密度P(ti)=1(m0+t),则式(14)可进一步转变为 (15) 则概率密度函数P(k)为 (16) 由幂律分布一般形式P(k)~k-γ可以看出,网络度分布P(k)符合典型幂律分布特征,且幂律指数γ=-2-p.P(k)与簇头比例p有密切关联,但与网络生长规模t无关,因此具有明显的无标度特征.不难发现,当p=1时,网络中所有节点均为簇头节点,此时网络等价为平面结构网络,此时P(k)=2k-3与m=1时的BA无标度网络度分布P(k)=2mk-3完全一致,P(k)正确性得到进一步验证. 2) 分簇WSN随机演化模型度分布 由演化机制可得,对于随机拓扑,当前时刻t网络中已存在簇头节点获得新加入连接概率完全一致,则对于簇头节点i,ki(t)满足动力学方程: (17) 与无标度演化模型证明过程类似,因篇幅限制,直接给出P(k)为 (18) P(k)为典型指数分布,与文献[19]有关随机网络度分布结论一致.根据理论分析所得度分布公式,当簇头比例p=0.2时,所提分簇WSN无标度与随机演化模型分别服从理论度分布P(k)=1.2k-2.2与P(k)=exp(-0.2k).与图3拟合后度分布曲线进行对比,不难得到实际度分布与理论度分布仅存在细微差异.这是由于在理论推导过程中,通常基于网络规模足够大这一理想情形,从而导致误差的产生.但随着网络规模的扩大,理论与实际度分布曲线的重合程度将进一步得到提升. 4.2 级联失效模型关键参数分析 根据负载分配策略,若簇内成员节点失效,将不会引发级联失效过程.因此,本节仅讨论簇头节点失效对网络拓扑影响.基于所提局域择优分配策略与节点负载-容量模型,为避免级联失效的发生,对于簇头节点j,应满足: (19) 根据Lj与Δji定义,不等式(19)可转化为 (20) 又因簇头占网络比例为p,仅考虑网络规模足够大情形,则不难得到cj=pkj与mj=(1-p)kj,代入式(20),化简可得: (21) [17]解析方法,根据网络度及概率论知识,可以得知: (22) 其中P(k′|ki)表示度为ki的簇头节点邻域中度为k′的条件概率,kmax和kmin分别为网络簇头节点度数的最大值与最小值.由4.1节关于度分布理论解析可知,所提分簇无标度演化模型与分簇随机演化模型的拓扑性质分别与BA网络[18]和ER网络[19]近似,而BA网络与ER网络均具有典型的度-度无关特性.因此,P(k′|ki)=k′P(k′)k.进而可得的另一种表达形式: (23) 将式(23)代入式(21),可得: (24) 关键阈值Tc为满足式(24)条件下T值最小值,则分别考虑α<1,α=1与α>1这3种情形: (25) 通过对式(25)解析,不难发现Tc随着A的增大而减小,随着p的增大而增大.结合Tc值越小网络级联失效抗毁性能越强这一结论,可得调节系数A与分簇WSN级联失效抗毁性呈正相关,簇头比例p与网络级联失效抗毁性能呈负相关,进一步验证了3.1节仿真结果.进一步观察式(25),不难发现,当α<1时,kmin是影响Tc值的主要因素,因而扩充簇-簇连接较少的簇头节点的容量能够更为有效地改善网络级联失效抗毁性能;同理,当α>1时,扩充拥有较多邻居簇头数量的簇头节点的容量,抗毁性能提升效果更为明显;当α=1时,Tc取值仅与k和k2有关、与kmin和kmax无关,因而对于执行哪种簇头扩容策略并不敏感.下一步我们将探讨当α取何值时Tc最小,即网络应对级联失效的抗毁性最优.首先分析α<1情形: (26) 可得Tc(α<1)>Tc(α=1);同理,针对α>1情形,可证得Tc(α>1)>Tc(α=1);因此,不难得到,当α=1时Tc最小,与3.1节仿真结果一致. 当前WSN抗毁性研究多从静态角度研究移除点或边对网络拓扑鲁棒性的影响,而忽略了网络拓扑因负载动态变化所引发的级联失效.因此,本文针对真实情形下普遍存在的分簇WSN,设计了参数可调的分簇WSN级联失效演化模型,并研究分簇无标度网络与分簇随机网络应对级联失效的抗毁性能.通过仿真分析与数据推导相结合的方式得到:1)分配系数A与网络级联失效性能正相关;2)簇头比例p与网络抗毁性能负相关;3)当调节参数α=1时,网络级联失效抗毁性能达到最优;4)当调节参数α<1时,选取簇-簇连接度较小的簇头节点扩充容量能够更为有效地提升网络级联失效抗毁性能;5)当调节参数α>1时,选取簇-簇连接度较大的簇头节点扩充容量抗毁性能提升效果更为明显;6)当调节参数α=1时,网络级联失效规模与簇头选取策略无关.研究成果对于预防WSN级联失效具有实际的参考价值.在现有研究基础上,如何有针对性地构建一种考虑扩充节点对象与扩充节点容量大小的综合优化策略将是未来研究的重点. 参考文献 [1]Li Jianzhong, Gao Hong. Survey on sensor network research[J]. Journal of Computer Research and Development, 2008, 45(1): 1-15 (in Chinese)(李建中, 高宏. 无线传感器网络的研究进展[J]. 计算机研究与发展, 2008, 45(1): 1-15) [2]Li Wenfeng, Fu Xiuwen. Invulnerability of wireless sensor networks[J]. Chinese Journal of Computers, 2015, 38(3): 625-647 (in Chinese)(李文锋, 符修文. 无线传感器网络抗毁性[J]. 计算机学报, 2015, 38(3): 625-647) [3]Wang Liangmin, Ma Jianfeng. Self-regeneration based method for topology control with intrusion tolerance in wireless sensor networks[J]. Journal of Computer Research and Development, 2009, 46(10): 1678-1685 (in Chinese)(王良民, 马建峰. 基于再生技术的无线传感器网络容侵拓扑控制方法[J]. 计算机研究与发展, 2009, 46(10): 1678-1685) [4]Fang Xiaolin, Shi Shengfei, Li Jianzhong. A disjoint multi-path routing algorithm in wireless sensor network[J]. Journal of Computer Research and Development, 2009, 46(12): 2053-2061 (in Chinese)(方效林, 石胜飞, 李建中. 无线传感器网络一种不相交路径路由算法[J]. 计算机研究与发展, 2009, 46(12): 2053-2061) [5]Li Yaqian, Yin Rongrong, Liu Bin, et al. Cascading failure research on scale-free fault tolerance topology in wireless sensor networks[J]. Journal of Beijing University of Posts and Telecommunications, 2014, 37(2): 74-78 (in Chinese)(李雅倩, 尹荣荣, 刘彬, 等. 无线传感器网络无标度容错拓扑的级联失效研究[J]. 北京邮电大学学报, 2014, 37(2): 74-78) [6]Yin Rongrong, Liu Bin, Liu Haoran, et al. Dynamic fault-tolerance analysis of scale-free topology in wireless sensor networks[J]. Chinese Journal of Physics, 2014, 63(11): 35-42 (in Chinese)(尹荣荣, 刘彬, 刘浩然, 等. 无线传感器网络中无标度拓扑的动态容错性分析[J]. 物理学报, 2014, 63(11): 35-42) [7]Fu Xiuwen, Li Wenfeng. Cascading failures of wireless sensor networks[C] //Proc of the 11th Int Conf on Networking, Sensing and Control (ICNSC). Piscataway, NJ: IEEE, 2014: 631-636 [8]Motter A E, Lai Y C. Cascade-based attacks on complex networks[J]. Physical Review E, 2002, 66(6): 065102 [9]Dobson I, Carreras B A, Newman D E. A loading-dependent model of probabilistic cascading failure[J]. Probability in the Engineering and Informational Sciences, 2005, 19(1): 15-32 [10]Nedic D P, Dobson I, Kirschen D S, et al. Criticality in a cascading failure blackout model[J]. International Journal of Electrical Power & Energy Systems, 2006, 28(9): 627-633 [11]Wang J W, Rong L L. Robustness of the western United States power grid under edge attack strategies due to cascading failures[J]. Safety Science, 2011, 49(6): 807-812 [12]Li Yong, Lü Xin, Tan Yuejin. Optimizing node capacity of campaign logistics networks based on cascading failures[J]. Complex System and Complexity Science, 2009, 6(1): 69-76 (in Chinese)(李勇, 吕欣, 谭跃进. 基于级联失效的战域保障网络节点容量优化[J]. 复杂系统与复杂性科学, 2009, 6(1): 69-76) [13]Yin Hongying, Quan Xiaofeng. The cascading influence law and influence scope of a failure in transportation networks[J]. Journal of Systems & Management, 2013, 22(6): 869-875 (in Chinese)(尹洪英, 权小锋. 交通运输网络级联失效影响规律及影响范围[J]. 系统管理学报, 2013, 22(6): 869-875) [14]Liu Y, Peng W, Su J, et al. Assessing the impact of cascading failures on the inter-domain routing system of the Internet[J]. New Generation Computing, 2014, 32(3/4): 237-255 [15]Liu H, Zhao L, Yin R, et al. A metric of topology fault-tolerance based on cascading failures for wireless sensor networks[J]. Journal of Information & Computational Science, 2011, 14(8): 3227-3237 [16]Yin R R, Liu B, Liu H R, et al. The critical load of scale-free fault-tolerant topology in wireless sensor networks for cascading failures[J]. Physica A: Statistical Mechanics and its Applications, 2014(409): 8-16 [17]Wang Jianwei, Rong Lili. Cascading failures on complex networks based on the local preferential redistribution rule of the load[J]. Chinese Journal of Physics, 2009, 58(6): 3714-3721 (in Chinese)(王建伟, 荣莉莉. 基于负荷局域择优重新分配原则的复杂网络上的相继故障[J]. 物理学报, 2009, 58(6): 3714-3721) [18]Barabási A L, Albert R, Jeong H. Mean-field theory for scale-free random networks[J]. Physica A: Statistical Mechanics and Its Applications, 1999(272): 173-187 [19]Newman M E J, Strogatz S H, Watts D J. Random graphs with arbitrary degree distributions and their applications[J]. Physical Review E, 2001, 64(2): 026118 Fu Xiuwen, born in 1987. PhD. His main research interests include the invulnerability of wireless sensor networks and the theory of complex networks. Li Wenfeng, born in 1966. PhD, professor and PhD supervisor. His main research interests include the technologies of Internet of things and robots, and wireless sensor networks. Duan Ying, born in 1983. PhD candidate. Her main research interests include the theory of industrial wireless sensor networks and data mining (able0607@163.com). Invulnerability of Clustering Wireless Sensor Network Towards Cascading Failures Fu Xiuwen1, Li Wenfeng2, and Duan Ying2 1(School of Vehicle & Transportation Engineering, Henan University of Science and Technology, Luoyang, Henan 471003)2(SchoolofLogisticsEngineering,WuhanUniversityofTechnology,Wuhan430063) Current researches of cascading failures of wireless sensor network (WSN) mainly focus on peer-to-peer (P2P) structure. However, in real scenarios most of sensor networks always collect and deliver environmental data via clustering structure. Therefore, through observing the heterogeneity of connections in clustered networks, we construct a cascading failure model of wireless sensor network by introducing the concept of “sensing load” and “relay load”. Besides that, we discuss the relevant features between key parameters of cascading model and invulnerability of two typical clustering topologies (i.e., scale-free topology and random topology). In order to constrain the scale of cascading failures, we also discuss how to select cluster heads to enlarge their capacity to achieve this purpose. The simulation and theoretical results show that the network invulnerability is negatively correlated to the proportion of cluster headspand positively correlated to the allocation coefficientA. When adjustment coefficientα=1, the invulnerability of the network is optimized. When adjustment coefficientα<1, choosing cluster heads with fewer cluster-cluster connections is a more efficient way to enhance the network invulnerability. When adjustment coefficientα>1, choosing cluster heads with more cluster-cluster connections is more cost-effective. When adjustment coefficientα=1, the scale of cascading failures is not related to the selecting schemes of cluster heads. wireless sensor network (WSN); cascading failures; clustering structure; invulnerability; scale-free topology; random topology 2015-06-09; 2015-09-21 国家自然科学基金项目(61571336);中央高校基本科研业务费专项资金项目(135118003) This work was supported by the National Natural Science Foundation of China (61571336) and the Fundamental Research Funds for the Central Universities (135118003). 李文锋(liwf@whut.edu.cn) TP393
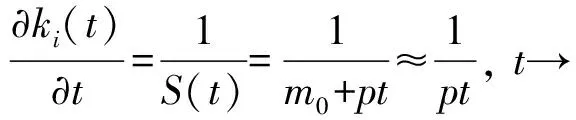
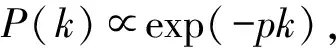

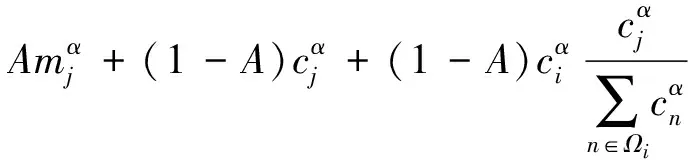
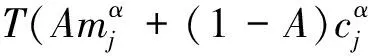

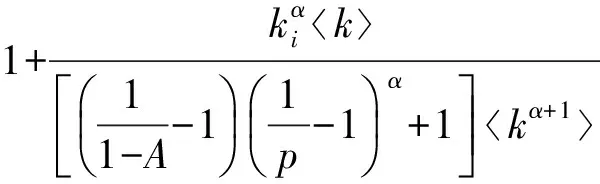
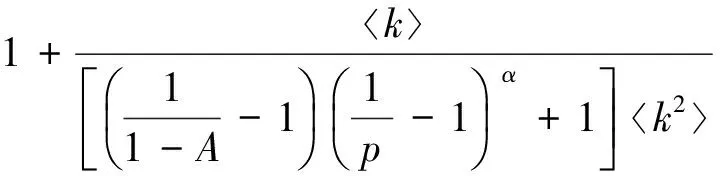
5 结 论



