初中数学基本活动经验习得刍议

【摘 要】基本活动经验是数学学习的前提，但又体现在数学学习的过程中。课堂教学既要注重基本活动经验的积累，又要关注基本活动经验的生成。从教学实践来看，学生对活动原理的理解程度会影响学生基本活动经验的习得，数学教学中有必要实施“慢教学”，以利于学生活动经验的习得。

【关键词】基本活动经验；经验习得；初中数学

【中图分类号】G633.6 【文献标志码】A 【文章编号】1005-6009（2016）54-0037-02

【作者简介】王强，南京市钟英中学（南京，210002）教师，一级教师。

《义务教育数学课程标准（2011版）》在原来的“双基”的基础上，提出了“四基”，即基础知识、基本技能、基本思想和基本活动经验，强调课程必须建立在学生原有的生活经验和数学活动经验的基础之上，这是数学课程实施的基点。自此，一段时间内“数学基本活动经验”成为数学教学研究的热点。例如，有论者认为，数学教学是在教师的指导下，师生共同开展的积极的数学思维活动，没有“经验”作前提，没有“数学活动”的内涵，就失去了数学课程的价值追求[1]。还有论者认为，在数学教学中，数学活动的形式或过程多种多样，但最基本的是“演绎活动”与“归纳活动”。在众多的数学活动经验中，最为基本的是归纳活动经验和演绎活动经验[2]。笔者从自己的教学实践出发，深刻体会到了数学基本经验的习得应该注意以下两个方面。

一、学生对活动原理的理解程度影响基本活动经验的习得

学生看到此题立刻知道将分子相加，这里面最大的难点在于初一的学生并不全知道等差数列求和公式，为此，教师在教学时设计了一个引例：求1+2+3+…+100的值。

教师引导学生观察，后面一个数比前一个数大1，因此最大数和最小数的和等于第二个数与倒数第二个数的和，依此类推，便可以发现“倒序相加”的原理。当然要得到这个发现需要留足时间给学生独立思考，适当的时候教师要给学生一些提示。在得到“倒序相加”的原理之后，便可以引导学生用这个原理来解决原题。笔者在班上对这道题目做了一个测试，先给出了引例，全班的学生经过引例的学习后，能够想到下面这个解法：

但是作为教师，笔者并不满意学生的这个解法，因为学生并没有真正关注到这道试题的特征，也没有体会到引例中做法的合理性，不能真正地应用活动原理来解题，也就谈不上真正有基本活动经验的积累。因此，笔者再次强调要深入思考引例，思考为什么这样做，这样做的前提是什么，它同原题有什么关联，经过生生之间一番激烈交流之后，终于有两个学生突破了思维的盲区，提供了第二种解法。

两个方法在本质上并没有什么区别，但是我们明显感觉到解法二更能体现“倒序相加”这一思想。这样的一次教学经历，让笔者明白了，学生对原理的观察和理解程度决定了他对基本活动经验习得的程度，因此我们在解题教学中要把最本质的东西讲透，尽量让学生能够有更深层次的理解。正如数学教育专家史宁中教授所说：我们必须清楚，世界上很多东西是不可传递的，只能靠亲身经历。智慧并不完全依赖于知识的多少，而是依赖知识的应用，依赖经验。由此，教师需要让学生在实际操作中磨炼。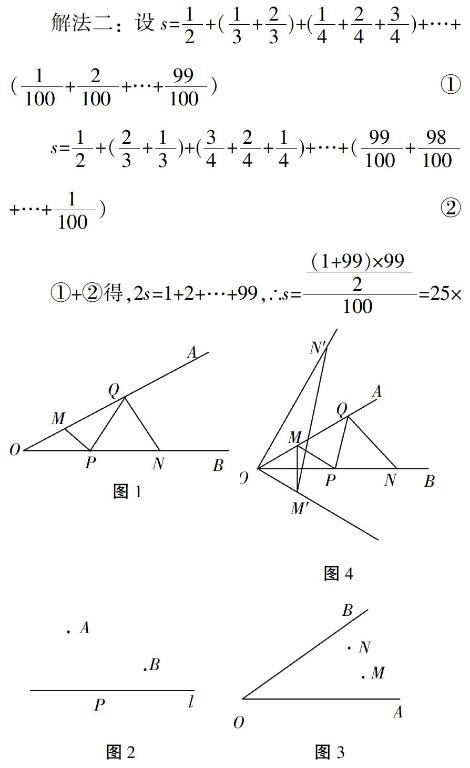

二、数学“慢教学”利于基本活动经验的习得

案例2：如图1，∠AOB=30°，点M，N分别在边OA，OB上，且OM=1，ON=3，点P，Q分别在边OB，OA上，则MP+PQ+QN的最小值是 。

这道试题属于一道中档题，但是要想在考场中做对此题，对学生还是一个比较大的考验。教师在教学时，可以从经典的几何模型出发来引入。

引例1：（将军饮马）如图2，在直线l的一侧有两点A，B，在直线l上找一点P，使得PA+PB最小。

引例2：如图3，点M、N在锐角∠AOB的内部，在OA边上求作一点P，在OB边上求作点Q，使得MP+PQ+QN最小。

对于引例1，我们不难发现，作其中一个定点关于定直线的对称点，再将这个对称点和另一个定点连起来交定直线的点就是我们要求的点。对于引例2，要找到两个动点。根据引例1的基本活动经验，一个点变成两个点做法应该类似，我们分别作两个定点的对称点，再将两个对称点连起来，交两条定直线的交点就是我们要求的点。而解决这两个引例的主要原理是两点之间线段最短，从这两个引例出发，就可以得到原题的解题思路：如图4，过点M、N分别向OB，OA作对称点M′，N′，连接M′N′，交OA于点Q，交OB于点P，根据两点之间线段最短，则M′N′即为MP+PQ+QN的最小值。

从引例1到引例2再到原题，是一个转化的过程。根据上文所述，教师在讲授这部分时，一定要讲清楚原理，引导学生做严格推导证明：为什么选择其他点不能使得和最小。这样才会使学生理解地更为深入。而这样一个讲解的过程正是一种“慢教学”，它的背后是数学基本活动经验习得的过程性。这种过程性具体表现在有机会去积累活动经验，有机会去体验长时间的思考，体验想不出来的痛苦，体验有想法的喜悦，体验解决问题的激动。课堂要能够慢下来，特别是在证明的关键处，只有在面对困难时的思维的高度集中，才能真正积累基本活动经验，从而在遇到较复杂的问题时，可以调动最接近的基本活动经验解决问题。

【参考文献】

[1]孔凡哲.基本活动经验的含义、成分与课程教学价值[J].课程·教材·教法，2009（03）：33-38.

[2]王新民，王富英，王亚雄.数学“四基”中“基本活动经验”的认识与思考[J].数学教育学报，2008（03）：17-20.

[3]G·波利亚.怎样解题：数学教学法的新面貌[M].涂弘，冯承天，译.上海：上海科技教育出版社，2002.