基于门限双幂变差的资产价格时点波动非参数估计

沈根祥

(1.上海财经大学经济学院，上海 200433；2.上海财经大学数理经济学教育部重点实验室，上海 200433)



基于门限双幂变差的资产价格时点波动非参数估计

沈根祥1,2

(1.上海财经大学经济学院，上海 200433；2.上海财经大学数理经济学教育部重点实验室，上海 200433)

估计带跳资产价格的时点波动时，需要用门限过滤方法消除跳的影响。在有限样本下，门限过滤会产生错滤偏误和漏虑偏误，降低估计精度。跳错滤产生的偏误可通过对错滤样本进行补足的方法进行纠偏，但由于发生时点未知，跳漏滤产生的偏误无法纠正，只能通过估计量设计来减少漏滤偏误。本文首次提出基于门限双幂变差的时点波动估计量，采用核平滑方法对资产价格时点波动进行非参数估计，有效减少跳错滤导致的偏误。采用随机阵列极限理论，本文证明了估计量的一致性和渐进正态性，在分析有限样本偏误的基础上，给出估计量的纠偏方法。蒙特卡洛模拟表明，本文给出的估计量，漏滤偏误明显小于基于二次变差构造的估计量，对时点波动估计的性质具有实质改进。采用Kupiec动态VaR精度检验对沪深300指数的实证分析表明，本文给出的时点波动估计更能描述资产收益的波动特征。

时点波动；Poisson跳；双幂变差；核平滑

1 引言

波动(Volatility)在金融理论和实践起着重要作用。连续时间金融认为，资产价格的波动具有随机性和时变性，是随机过程。波动过程在时间点上的值称为时点波动(Spot Volatility)。方差的不可观测性使波动成为隐变量(Latent Variable)，需通过资产价格样本间接进行估计。在较低频率下(例如周、月等)，可采用ARCH类模型和SV模型等参数模型研究资产价格的波动，并采用极大似然方法估计模型参数。近年来，在对高频数据的研究中，时点波动的估计和推断显现出重要性。鉴于时点波动不可观测的特点，人们尝试采用非参数方法估计时点波动并将估计值作为“样本”，使波动过程变得“可观测”，据此直接对波动进行分析或者以此作为进一步分析的基础，以克服波动不可观测的限制。Fan Jianqing和Wang Yazhen[1]采用核平滑技术给出高维随机波动模型时点波动的一致估计及其渐进分布，Kristensen[2]从RV的性质出发给出扩散过程时点波动估计及其渐进分布。Bandi和Reno[3]、Bollerslev和Todorov[4]在研究中把时点波动作为输入变量，Ait-Sahalia等[5]在研究杠杆效应时，讨论了时点波动估计存在的各种偏误对研究结果的影响。用非参数方法估计时点波动，对资产价格模型的约束少，与GARCH和SV模型相比，能减少模型设定误差。

在高频交易数据中，资产价格经常发生跳跃[6]。跳的存在严重影响波动的估计准确性，包括积分波动(Integrated Volatility)和时点波动。文献中采用双幂变差和门限二阶变差两种方法消除跳的影响。沈根祥[7]借助门限方法[8]，采用截尾收益平方构造时点波动估计量来消除跳的影响，并允许资产价格存在杠杆效应，推广了Fan Jianqing和Wang Yazhen[1]和Kristensen的结论。门限截尾基于连续资产价格过程在很短时间内的改变量已接近1的概率不超过某个门限值，并将超过临界值的观测值作为跳过滤掉。门限方法在跳过滤时会产生的两类错误：错滤和漏滤。将不是跳的超过门限值价格改变量作为跳滤掉会产生错滤，错滤导致估计量的下偏误，而不能将小于门限值的跳过滤掉会产生漏滤，漏滤导致估计量的上偏误。给定门限值后，两类偏误此消彼长：过大(小)的门限值在减少(增加)错滤偏误的同时，将增加(减少)漏滤偏误。门限值给定后，哪些价格改变量被滤掉是知道的，可采用不同的方法对错误过滤掉的样本进行补足以减少错滤偏误。Corsi等[9]采用价格改变量的条件数学期望补充被滤掉的样本，沈根祥[7]则采用邻近未被滤掉的价格改变量均值补充错滤样本。采用门限方法对跳进行过滤时，未被滤掉跳的位置是不知道的，因此不能进行修正以减少漏滤偏误。错滤造成的估计偏误大于漏滤造成的偏误，往往取较大门限值以减少错滤偏误，这势必增加漏滤偏误[7]。如何减少跳漏滤导致的估计偏误，是时点波动估计需要解决的问题。本文将消除跳影响的两种方法结合起来，首次采用门限双幂变差构造时点波动估计量，以减少跳漏滤带来的估计偏误。

国内对金融资产价格波动的研究大多以离散时间GARCH模型和SV模型为主，近年来出现的基于高频数据的研究多为RV和IV的估计并以此为基础进行含跳资产价格过程的建模。陈浪南和孙坚强[10]采用GARCH跳模型对上证指数的实证研究表明，指数中的Poisson跳存在时变特征和群集效应，刘志东和陈晓静[11]使用无限活跃Levy纯跳CGMY模型研究上证综指的跳规律，采用GMM方法估计模型参数，发现上证综指中跳活跃BG指数小于1。王春峰等[12]基于BN-S方法对上证综指已实现方差进行分解，研究跳跃性方差的统计性质，采用HAR-RV-CJ模型对已实现方差进行预测，陈国进和王占海[13]将沪深300指数的已实现方差分解为连续性方差和跳跃性方差并分别建立模型，杨科和陈浪南[14]用门限双幂变差估计积分方差对BN-S方法进行改进后对上证综指5分钟高频数据进行跳存在性检验，并使用ACD模型和ARCH模型对波动率中的跳行为进行研究。沈根祥[6]采用门限双幂变差改进Lee和Mykland[15]的方法，对沪深300指数中泊松跳跃行为进行了逐时点检验和统计分析。杨科等[16]将波动分解为跳波动和积分波动，并构造包含跳的AHAR-RV-CJ模型对中国股市的已实现波动率进行预测，并与其它波动预测模型进行比较。时点波动估计方面，沈根祥[7]采用以门限二阶变差为基础，采用核平滑技术构造了跳扩散过程的时点波动非参数估计。

现有文献中的时点波动估计均以价格过程的二阶变差为基础进行构造，本文首次以双幂变差为基础，结合跳过滤的门限方法构造跳扩散过程时点波动的非参数估计，以最大程度减少跳漏滤带来的估计偏误。采用随机阵列极限定理证明了估计量的一致性和渐近正态性。为更有效减少跳错滤带来的估计偏误，本文采用跳发生点附近价格改变量的中位数作为被滤跳样本的补充。蒙特卡洛模拟显示，本文构造的估计量能显著减少跳漏虑带来的估计偏误，采用动态VaR精度检验对沪深300指数的实证分析表明，本文给出的时点波动估计更能描述资产收益的波动特征。

2 资产价格过程模型设定

dpt=μtdt+σtdwt+dJtt∈[0,T]

(1)

资产价格模型大多为右连续左极限存在的随机过程，满足条件A1.[17]。本文中的估计量基于核平滑非参数方法，对核函数和带宽作如下假设:

K1. 核函数K(·)为非负实值连续可导函数，且导数有界，并满足：

∫RK(z)dz=1, ∫RzK(z)dz<∞, ∫RKm(z)dz≡Km<∞, m=2,4

K2. 带宽(Bandwidth)h满足：(i)h→0；(ii)当n→∞、h→0时，nh→∞，nh2log(1/h)→0。

3 时点波动估计量及其性质

3.1 具有杠杆效应的扩散过程时点波动估计量

对任意时点t∈(0,T)，设Kh(s)=h-1K[(s-t)/h]为平滑核。首先定义资产价格过程不存在跳的时点波动估计量：

(2)

定理1：设pt为连续过程，dJt=0。如果条件(A1.)、(K1.)和 (K2.)满足，对∀t∈(0,T)，有：

(3)

由(3)第一式得出：

(4)

为叙述方便，设：

(5)

(6)

并且求和项均为鞅差序列，便于采用随机分析工具。

其中：

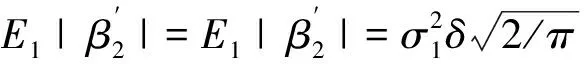
关于Fi可测。根据Jacod 和 Shiryayev[19]，需要证明：

由此得出：

将D1变形为：

由条件(A.)可知σt是连续Ito半鞅[20]。根据Ito半鞅连续模得出|σi-1-σi|≤c[δlog(1/δ)]1/2，并根据布朗运动连续模得出：

对于D2，采用如下分解：

本定理的证明与Corsi[9]、Reno和Bandi[3]等核心定理的证明采用了类似的理论工具，但存在区别。Corsi、Reno和Bandi构造的是已实现波动估计量，是时间区间上波动的总和，本文构造的是时点波动估计量，采用了核平滑方法，需要证明核权重的随机变量部分和的中心极限定理，其中D2收敛于0的证明为新增内容。

3.2 含Poisson跳的资产价格时点波动估计量

由Poisson过程的性质可知，[0,1]区间内只有有限次跳跃发生，当n→∞时，相邻区间(ti-1,ti]和(ti,ti+1]中至多有一个区间内发生跳。设跳跃发生次数为N，最大跳幅为M。|Δip|和|Δi+1p|只有一个包含跳，另一个为连续扩散过程的增量，不妨设为|Δip|。对|Δip|利用扩散过程连续模性质，再根据核函数K的有界性，得出：

T. 门限函数ϑ(δ)满足：limδ→0ϑ(δ)=0，limδ→0[δln(1/δ)]/ϑ(δ)=0。

(7)

定理3：设资产价格过程pt满足式(1)，且dJt≠0。如果条件(A1.)、(A2.)、(K1.)和(T.)满足，则对∀t∈(0,T)

∑iKh(ti)|Δip||Δi+1p|I{(Δip)2≤ϑ(δ)}

I{(Δi+1p)2≤ϑ(δ)}=∑iKh(ti)|Δip||Δi+1p|I{(Δip)2≤ϑ(δ)}I{(Δi+1p)2≤ϑ(δ)}I{Ni=0,Ni+1=0}+∑ti≠tKh(ti)

|Δip||Δi+1p|I{(Δip)2≤ϑ(δ)}I{(Δi+1p)2≤ϑ(δ)}I{Ni≠0or Ni+1≠0}=∑iKh(ti)|Δipc||Δi+1pc|+∑ti≠tKh(ti)|Δip||Δi+1p|I{Ni≠0 Ni+1≠0}

设NT为(0,T)上Poisson跳发生次数，根据泊松过程性质NT<∞ a.s.，因此：

Mancini[8]提出的门限过滤技术多用于区间上已实现波动的估计，定理3将这种方法用于时点波动估计量中心极限定理的证明，需要证明带核权重滤掉项的渐近可忽略性。

定理3中的结论是δ=n-1→0的渐进结论，当n有限时存在跳过滤导致的有限样本偏误。偏误有两种，连续扩散过程产生的价格改变量超过门限值被当做跳错误过滤掉，Poisson跳过程产生的价格改变量没有超过门限值而没有被过滤，前一种造成向下偏误，后一种则造成向上偏误。

3.3 跳过滤偏误及其纠正

A1i=|Δipc|Δi+1pc|I{(Δipc)2>ϑ(δ)or(Δi+1pc)2>ϑ(δ)}

A2i=|Δip|Δi+1p|I{Ni≠0 or Ni+1≠0}

I{(Δip)2≤ϑ(δ),(Δi+1p)2≤ϑ(δ)}

其中A1i为错滤项，A2i为漏滤项。对于A2i，根据Poisson过程的性质和沈根祥[7]得出：

E(A2i)≤ϑ(δ)P[(Ni≠0)∪(Ni+1≠0)]=ο(δ)

对于A1i，根据Holder不等式和沈根祥[7]得出：

错滤项和漏滤项的期望值都是δ的无穷小量。

尽管错滤和滤漏偏误都是无穷小量，但前者趋于0的速度远低于后者[7]。为减少偏误，对错滤进行纠偏。具体做法是当(Δipc)2>ϑ(δ)时，用附近区间上价格改变量绝对值|Δi±kp|,k=1,2的中位数代替|Δip|。此外，估计式的权重项Kh(ti)是核函数积分的离散化，和并不等于1，为减少偏误，将(7)式关于权重标准化，得出跳错滤纠偏后时点波动估计量：

(8)

其中med表示中位数。作为滤掉价格改变量的补足，采用中位数比采用平均值更稳健[7]。

3.4 与其他估计量的比较

3.5 最优带宽和核函数

4 蒙特卡洛模拟

本部分通过随机模拟来评价时点方差估计量的效果，考察Poisson跳对时点波动估计的影响以及时点波动估计量的有限样本表现。

4.1 模拟数据

表1 滤偏误比较

杠杆效应通过价格过程布朗运动w和波动过程布朗运动B的相关性来刻画，相关系数为ρ。模拟以沪深300指数日内五分钟交易为对象，时间跨度为一年。参数取值与模拟数据产生的步骤与沈根祥[7]相同。

4.2 最优带宽和门限函数

本文采用沈根祥[7]中带宽参数的确定方法，取带宽为h=Cn-0.4999。交叉验证表明，对应ρ值-0.25、-0.5和-0.75的最优带宽参数c0分别为1.70、0.45和0.50，并且不受跳频度参数λ的影响。选取合适的门限函数有利于减少有限样本偏误。本文采用沈根祥[7]的门限函数ϑ(δ)=12000-0.99≈8.95×10-4。

4.3 时点波动估计跳漏滤偏误比较

对表1中结果给出如下解释：

跳频度对漏滤偏误的影响：跳频度对漏滤偏误有显著影响，频度越高，漏滤偏误越大。从表1中看出，λ的值从1/240(每周发生一次跳)逐渐增加1/24(每两个小时发生一次跳)时，对应的漏滤偏误随之增加。跳频度增加时，跳发生次数增加，漏滤发生次数增加，导致漏滤偏误增加。

杠杆效应对漏滤偏误的影响：杠杆效应强度影响漏滤偏误，杠杆效应越强，漏滤偏误增大。从表1中看出，ρ的大小从0.25增加到0.75时，对应的漏滤偏误在大多情况下是增加的，只有在λ=1/24对应的ρ从0.5增加到0.75时，Bias1有稍微减少，以及λ=1/48对应的ρ从0.5增加到0.75时，Bias有稍微减少(表1中的下划线数据)。

5 实证分析—基于VaR测度的时点波动估计比较

GED分布为对称分布，均值为0，β<2时比正态分布有更厚的尾部，β=2时GED分布为正态分布，β→∞时，GED的极限分布为[-31/2,31/2]上的均匀分布，据此可以充分刻画金融数据的厚尾性。

设N0为rt序列中LSt取0的个数，N1为LSt取1的个数，N=N0+N1为序列长度，τ=N1/N称为失败率，τ越接近p表明VaR估计越精确。据此Kupiec构造极大似然比检验统计量LR：

LR=-2(ln[(1-p)N0pN1]-ln[(1-τ)N0τN1])

在原假设H0:τ=p下，LR～χ2(1)。

表2 VaR精度比较

**表示已0.01显著水平拒绝原假设。

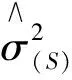
6 结语

本文以价格改变量的双幂变差为基础，给出一类新的资产价格时点波动估计量，显著减少跳过滤带来的漏滤偏误。采用随机阵列中心极限定理，本文得出估计量的一致性和渐进正态性。蒙特卡洛随机模拟的结果表明，无论是以单路径累积偏误均值为标准，还是以平均路径累积偏误为标准，本文给出估计量的漏滤偏误在所有情况下都显著小于以二次变差为基础构造的时点波动估计量，使跳扩散过程资产价格时点波动估计量的性质得到实质性改进。基于沪深300指数的VaR精度kupiec检验进一步表明，与门限二次变差时点波动估计相比，本文给出的时点波动估计更能刻画资产收益的风险特征。

[1] Fan Jianqing, Wang Yazhen. Spot volatility estimation for high-frequency data[J]. Statistics and its Interface, 2008,1(2):279-288.

[2] Kristensen D. Nonparametric filtering of the realized spot volatility: A kernel-based approach[J]. Econometric Theory, 2010,26(1): 60-93.

[3] Bandi M, Reno R. Time-varying leverage effects[J]. Journal of Econometrics, 2012, 169(1):94-113.

[4] Bollerslev T, Todorov V. Estimation of jump tails[J]. Econometrica, 2011, 79(6):1727-1783.

[5] Ait-Sahalia Y, Fan Jianqing, Li Yazhen. The leverage effect puzzle: Disentangling sources of bias at high frequency[J]. Journal of Financial Economics, 2013, 109(1):224-249.

[6] 沈根祥. 沪深300指数跳的逐点检验及动态分析[J]. 中国管理科学，2012, 20(1):43-50.

[7] 沈根祥. 带Poisson跳和杠杆效应的资产价格时点波动非参数估计[J]. 数量经济技术经济研究，2012, 29(12):82-96.

[8] Mancini C. Non-parametric threshold estimation for models with stochastic diffusion coefficient and jumps[J]. Scandinavian Journal of Statistics, 2009, 36(2):270-296.

[9] Corsi F, Pirin D, Reno R. Threshold bipower variation and the impact of jumps on volatility forecasting[J]. Journal of Econometrics, 2010, 159(2):276-288.

[10] 陈浪南,孙坚强. 股票市场资产收益的跳跃行为研究[J]. 经济研究，2010, (4):54-66.

[11] 刘志东,陈晓静. 无限活动纯跳跃Levy金融资产价格模型及其CF-CGMM参数估计与应用[J]. 系统管理学报，2010, 19(4):428-438.

[12] 王春峰,姚宁,房振明,等. 中国股市已实现波动率的跳跃行为研究[J]. 系统工程，2008, 26(2):1-6.

[13] 陈国进,王占海. 我国股票市场连续性波动与跳跃性波动实证研究[J]. 系统工程理论与实践，2010, 30(9):1554-1562.

[14] 杨科,陈浪南. 基于C-TMPV的中国股市高频波动率的跳跃行为研究[J]. 管理科学，2011, 24(2):103-112.

[15] Lee S S, Mykland P A. Jumps innancial markets:A new nonparametric test and jump dynamics[J]. Review of Financial Studies, 2008,21(6): 2535-2563.

[16] 杨科,田凤平,林洪. 跳跃的估计、股市波动率的预测以及预测精度评价[J]. 中国管理科学，2013,21(3):50-60.

[17] Barndorff-Nielsen O E, Shephard N. Econometrics of testing for jumps in financial economics using bipower variation[J]. Journal of Financial Econometrics, 2006, 4(1):1-30.

[18] Mykland P A, Zhang Lan. The econometrics of high-frequency data[M]// Kessler M, Lindner A, Sorensen M. Statistical methods for stochastic differential equations, United Kingdom:Talor & Francis, LLC, 2012.

[19] Jacod J, Shiryaev N. Limit theorems for stochastic processes[M]. Berlin:Springer Science & Business Media, 2003.

[20] Barndorff-Nielsen O, Graversen S, Jocod J, et al. A central limit theorem for realized power and bipower variations of continuous martingales[M]//Kabanov Y, Lipster R, Stoyanov J. From stochastic calculus to mathematical finance. Heidelberg:Springer, 2006:33-68.

[21] Kupiec P. Techniques for verifying the accuracy of risk measurement models[J]. Journal of Derivatives, 1995, 3(2):73-84.

Nonparametric Estimation for Spot Volatility of Asset Price Using Bipower Variations

SHEN Gen-xiang1,2

(1.School of Econmics,Shanghai University of Finance and Economics,Shanghai 200433,China;2.Key Laboratory of Mathematical Ecnomics(SUFE),Ministry of Education,Shanghai 200433,China)

The threshold jump-annihilating method to estimate spot volatility of jump-diffusion asset price processes can miss the small jumps and bring about upward bias[Corsi & Reno, JoE 2010 ]. In this paper, a new spot volatility estimator of asset prices is proposed based on bipower variation that reduces significantly finite-sample upward bias from jump-filtering-missing. The consistency and asymptotic normality is established. An extensive Monte Carlo simulation shows that the estimator in the paper outperforms the others in literature. The empirical study using Kupiec test based on sample from CSI300 shows that our spot volatility estimator can capture the feather of market risk more accurately.

Spot Volatility; Poisson Jumps; Bipower Variation; Kernel Smoothing

1003-207(2016)01-0021-09

10.16381/j.cnki.issn1003-207x.2016.01.003

2014-03-17；

2015-02-14

教育部人文社科研究规划基金资助项目(13YJA790095)资助；上海财经大学数量经济教育部重点实验室开放课题资助(201301KF01)

简介：沈根祥(1964-)，男(汉族)，河南许昌人，上海财经大学教授，博士生导师，研究方向：金融计量学，金融市场数量分析，E-mail:syxman@shufe.edu.cn.

F830.9

A