考虑残值变化和顾客异质性的零售商定价与库存决策
2016-12-19王夏阳
王夏阳,傅 科,吁 彬
(中山大学岭南学院,广东 广州 510275)
考虑残值变化和顾客异质性的零售商定价与库存决策
王夏阳,傅 科,吁 彬
(中山大学岭南学院,广东 广州 510275)
本文研究策略型消费者对零售商的定价和库存决策的影响。与以往的研究假设残值固定不变,且消费者均为策略型消费者不同的是,本文考虑了顾客的异质性以及残值由清仓期库存决定这一特点。本文的研究表明:在消费者均为策略型消费者,且清楚零售商将采取残值定价策略的情况下,零售商可以通过数量保证策略来提高自身的期望利润,降低库存订货量。在考虑顾客异质性的条件下,当零售商采取估值定价策略时,零售商的最大期望利润与短视型消费者在市场上的比例成正相关。并且,存在一个唯一的阈值点,当短视型消费者在市场上的比例高于这一阈值点时,估值定价策略优于保留价格定价策略,反之,则保留价格定价策略更优。
策略型消费者;理性预期均衡;残值;顾客异质性
1 引言
对于易逝性产品而言,在需求不确定的情况下,零售商很容易订购过多的产品。由于产品的生命周期有限且库存成本较大,零售商往往会选择在销售季末通过降价促销的方式来刺激消费者购买产品,降价促销也因此被视为零售商对易逝品定价的一种有效的方式。与此同时,越来越多的消费者在购买产品之前会估计产品降价的可能性,并比较立即购买与延迟购买产品所获得效用的大小,从而确定最佳购买时机,这样的消费者被称为策略型消费者(Strategic Consumer)。企业降价促销的初衷是以低价商品吸引消费者,从而实现薄利多销,或是在季末清仓以减少损失。然而,策略型消费者的存在则会导致传统的促销效果发生改变,因此策略型消费者的行为已经引起了企业界和学术界的广泛关注。近年来,一些企业已经在定价与库存等决策中逐渐开始考虑顾客策略行为的影响,并试图设计一些机制来有效减少顾客策略行为,进而提高企业绩效。例如,面对策略性消费者时,采用数量承诺、价格承诺、模糊销售策略、快速响应等举措将有利于企业提高盈利[1-5]。其中,西班牙的国际时尚服饰制造商和连锁零售商ZARA就采用了快速响应策略。由此可见,对策略型消费者的研究具有重要的理论和实践意义。
有关消费者策略行为的分析首先出现在经济学的耐用品垄断研究中[6-8]。近年来,人们对策略型消费者的研究开始拓展到企业运营管理领域,并在易逝品的定价与库存决策领域引起了广泛的关注[1-5,9-20]。其中,Zhang Dan和Cooper[10]分析了消费者策略行为对企业动态定价和供给决策的影响。Aviv和Pazgal[11]研究了预先声明的固定折扣定价机制和基于库存量大小的相机定价机制,并采用数值实验分析了二者对零售商收益的影响。Su Xuanming和Zhang Fuqiang[1]的研究则更具代表性,并引致了随后的一系列拓展研究[2-5,12-22]。Su Xuanming和Zhang Fuqiang[1]的研究假设消费者均为策略型消费者,在理性预期均衡的框架下,应用报童模型,研究了随机需求下的零售商定价与库存决策问题。后续的一系列拓展研究进一步考虑了预算约束、不确定性与风险因素、价格保证机制、模糊销售策略、快速响应、稳健性定价、产品的预售策略等机制对策略型消费者行为以及企业绩效的影响[2-5,12-24]。其中,Jerath等[3]证明,当面对策略型的消费者时,企业实行不透明的模糊销售策略,可以提高零售商的利润水平。Cachon和Swinny[5]的研究表明,在面对策略型消费者时,对时尚产品供应链采用快速响应、改进设计将有利于企业提高盈利。Mersereau和Zhang Dan[14]的研究认为,在策略型消费者和短视型消费者按比率存在的情况下,当产能较小时,企业甚至在定价时可以直接忽略策略型消费者的存在,此时仍然可以达到一个很高的绩效。Li Qian和Zhang Dan[16]则从信息更新的角度研究了提前预售策略对策略型消费者行为的影响。
对文献的梳理发现,早期的一些研究主要是将顾客策略行为引入到企业的定价机制与库存补货机制中[1,9-11,17]。近期的研究逐渐关注起顾客策略行为与数量承诺、价格承诺与保证机制、不确定性与风险、供应链渠道策略等方面,研究成果也日益丰富[2-5,12-24]。然而,除了Aviv和Pazgal[11]在相机定价策略中考虑了剩余库存量的影响之外,这些研究均假设残值是固定的,并且通常假设消费者要么全部是策略型消费者,要么全部是短视型消费者。Aviv和Pazgal[11]虽然考虑了剩余库存量的影响,却将库存视为既定,仅研究了定价问题。刘晓峰和徐贤浩[19]在有关易逝品两期定价机制的研究中同时考虑了策略型消费者和短视型消费者,但是这一研究也将库存视为既定,仅讨论定价问题。事实上,对于服装等经常面临季末清仓问题的企业而言,期末的剩余库存与季末折扣价对企业的赢利十分重要,因此在决策时不会忽视二者的关系,将季末折扣价视为一个固定值。例如,Caro和Gallien[25]就专门针对ZARA在欧洲市场的清仓期定价问题进行了优化与实验研究。虽然这一研究具体而深入,但是其研究重心主要放在服装企业的季末清仓期定价问题上,而将库存视为沉淀成本,没有考虑整个销售季节的库存决策问题,也没有考虑消费者的异质性。然而,一个更加符合现实的假设应该是同时考虑残值随库存量的变化和消费者的异质性。
有鉴于此,本文的研究集中在当存在消费者策略行为,且季末折扣价(即产品的残值)随剩余库存量变化时,零售商的定价与库存决策问题。本文的研究创新主要在于在模型中考虑了顾客的异质性以及残值由清仓期库存决定这一特点,这与以往的研究假设残值固定不变,且消费者通常均为策略型消费者形成了本质的区别。本文还在残值由清仓期库存决定这一假设下进一步讨论了采取信息更为透明的数量保证机制是否会侵蚀零售商利润的问题。本文的结构安排如下:在第2部分,本文建立了三个模型对此进行分析。在2.1部分,假设消费者是同质的,建立了考虑残值由清仓期库存决定的定价与库存决策模型,并对比分析了数量保证机制对零售商定价与库存决策乃至企业绩效的影响;在2.2部分的模型中,本文假设残值固定不变,着重分析了顾客的异质性对零售商定价与库存决策的影响;在2.3部分的模型中,本文同时考虑了残值变化和顾客的异质性。第3部分是数值实验,在数值实验部分,本文进一步讨论了零售商的定价、库存决策过程以及策略型消费者所占比例及不同的定价策略对零售商的利润的影响。
2 模型建立与讨论
2.1 考虑残值由清仓期库存决定情况下的零售商决策问题
在Su Xuanming和Zhang Dan[1]的文章中,假设产品在清仓期的残值为s为常数。然而,在实际生活中,当产品因为错过销售旺季降价出售时,零售商往往根据清仓期的库存多少来调整其价格。一般来讲,清仓期的剩余库存越多,零售商会把此时的价格(即残值)调整得越低[11]。例如,ZARA在欧洲市场的清仓期定价决策中采取的就是这一做法,即为了在一轮清货中获得更大的销量会将价格进一步调低[25]。有鉴于此,本文假设清仓期的价格(即残值)s是由期末剩余量Max(Q-X,0)决定的,并且s=p-αMax(Q-X,0)。其中,p为产品在销售期初的价格,Q为产品的订购量,X为市场的随机需求,α是某一常数。此时残值s是一个随机变量,随着需求X的变化而变化。
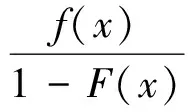
首先考虑不存在数量保证的情形,即零售商不向消费者承诺产品的可得性,此时零售商和顾客之间存在着静态博弈的关系。根据理性预期均衡的定义[1,4],双方的决策过程为:(1)零售商预期保留价格,消费者预期产品可得性和产品的残余价值;(2)双方基于预期同时做出最优决策;(3)达到均衡时,预期与实际的一致。
假设零售商对顾客保留价格的预期为ξr;消费者对购买到清仓期降价产品的可能性的预期为ξprob,对残值的预期为s0。零售商对价格的最优决策是根据对保留价格的预期,将价格定为保留价格,即p=ξr。因而,零售商在进行最优数量决策时,将价格视为既定。
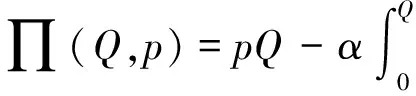
消费者的决策目标是权衡购买时机以最大化其消费者剩余,即Max{v-p,(v-s0)ξprob}。由此易知,给定ξprob,保留价格为r=v-(v-s0)ξprob。
在达到理性预期均衡时,预期与实际符合一致性条件。因而,消费者对购买到清仓期降价产品的可能性的预期满足ξprob=F(Q),零售商对消费者保留价格的预期满足ξr=r,消费者对残值预期s0的满足s0=Es,其中Es为随机变量s的期望。此时,消费者在销售期购买产品的消费者剩余和在清仓期购买产品的期望剩余是相等的,所以产品在销售期初的销售价格满足v-p=(v-s0)ξprob。并且,清仓期时的残值期望值可以表示为:
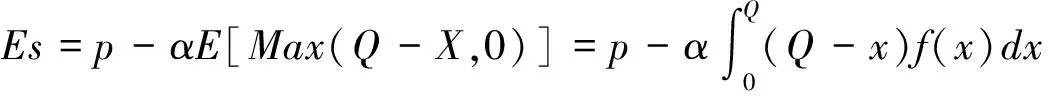
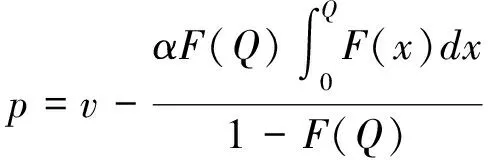

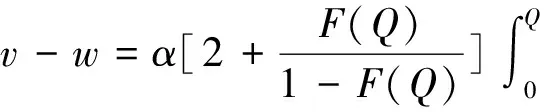
由以上分析,可以得出定理1。
定理1:不存在数量保证机制的情况下,零售商的利润函数∏(Q,p)存在唯一的理性预期均衡解组合(Q*,p*)。
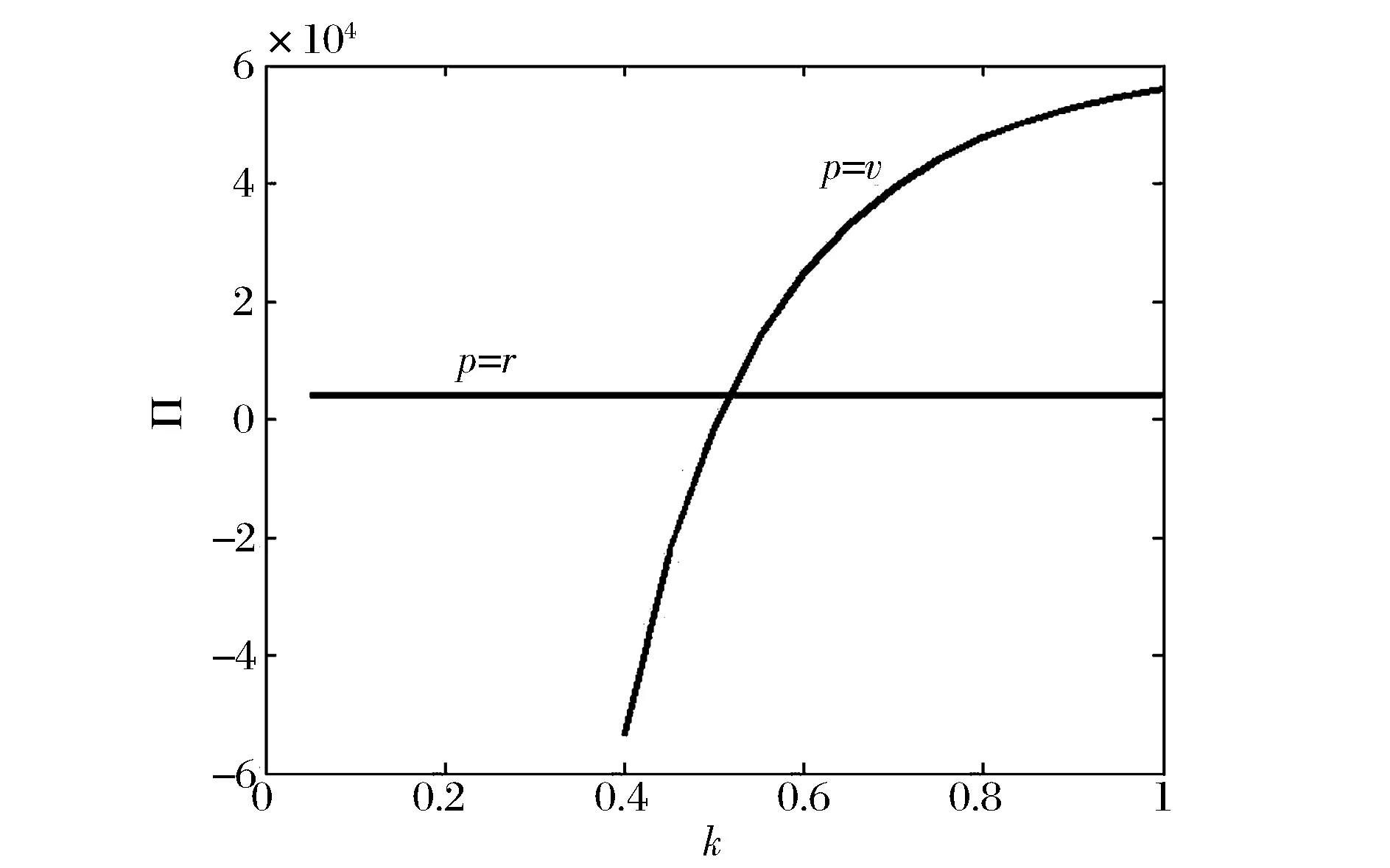
接下来考虑零售商向策略型消费者提供数量保证的情形。此时,清仓期购买到残值价格产品的概率F(Q)是公开信息,并且策略型消费者根据以往零售商在清仓期的降价历史经验,也清楚地了解到零售商的清仓期降价策略s。在这一情形下,消费者知道只有在市场的需求量小于零售商的订购量的时候,即X 所以,此时消费者的保留价格满足:v-r=(v-Es)F(Q)。 作为博弈的另一方,零售商清楚地了解到策略型消费者的选择策略,为了获得最大预期利润,零售商把销售期的价格p定在策略型消费者的保留价格r上。 此时,零售商的利润可以表示为关于Q的函数: 对上式进行求导,得: 因而,可以得出定理2。 由以上分析,可以得出命题1。 综上所述,在考虑残值的变化时,零售商和策略型消费者的博弈可以达到唯一的理性预期均衡。在残值变化情景下,假设消费者知道零售商的残值定价策略,零售商提供数量保证这一策略将使得零售商仅有一种最佳的订购量。与不提供这一策略比较,提供这一策略有助于提高零售商的期望利润,并降低了库存订货量。因而,即使残值会随着库存量做出调整,在消费者均为策略型消费者时,数量保证机制的存在不仅不会侵蚀零售商的利润,反而有益于零售商。但是,此时的产品在销售期初的定价会更高。 2.2 考虑消费者异质性的零售商决策问题 在2.1中,我们假设消费者是同质的,在本部分,我们考虑市场上同时存在短视型消费者和策略型消费者的情况。为了使问题更清晰,在这一部分,假设残值是固定的,仅考虑消费者的异质性问题。在2.3部分,将进一步考虑残值的变化。 假设短视型消费者和策略型消费者的数量比为k:(1-k),其中k为短视型消费者占所有消费者的比率,且0 双方的决策过程为:(1)零售商预期保留价格,策略型消费者预期产品可得性;(2)零售商综合考虑策略型消费者和短视型消费者的消费选择行为,确定最优定价策略和最优库存决策;短视型消费者直接做出是否购买的决策,策略型消费者则基于预期做出最优决策;(3)达到均衡时,预期与实际的一致。 零售商为了预期的利润最大,只有两种定价的策略。其一,零售商把价格定在策略型消费者的保留价格r上。其二,零售商把价格定在消费者的估价v上。零售商把价格定在两者之外的任何地方都没有好处。随后本文将就这两种定价策略分别进行讨论。 假如把销售期的价格p定在保留价格r和估值v之间,市场上的短视型消费者会选择在销售期购买产品,而策略型消费者会选择在清仓期购买产品,消费者的购买行为和把销售期的价格p定在估值v上是一致的。然而这种定价策略获取的利润显然低于销售期的价格p定在估值v上的利润。 假如销售期的定价p低于保留价格r,市场上消费者的购买行为和把销售期的价格p定在保留价格r上是一致的。然而这种定价策略获取的利润显然低于销售期的价格p定在保留价格r上的利润。 假如销售期的定价p高于估值v,那么市场上就不会有购买的行为,显然不会产生利润。因此,零售商只有两种定价的策略。 当零售商把价格定在策略型消费者的保留价格r上时,所有的消费者都可能会在全价期购买产品,零售商可能可以获取更大的利润。此时,零售商的利润函数与Su Xuanming和Zhang Dan[1]中的零售商利润函数相同,即:∏C(Q,p)=(p-s)E(X∧Q)-(w-s)Q。 故Q0>kQC。 由以上分析,可以得出命题2。 接下来,本文将进一步讨论策略型消费者所占比例对定价策略选择的影响。 对于任意的0 2.3 考虑残值由清仓期库存决定情境下的异质性问题 在这一部分,我们在2.2中引入顾客的异质性的基础上,同时考虑2.1中的残值由清仓期库存决定这一现实假设。双方的决策过程与2.2类似,主要区别在于策略型消费者在决策之前除了预期产品的可得性外,还需要对产品的残余价值做出预期。 与2.1的假设一致,零售商根据销售季末的库存量决定清仓期的价格,即s=p-αMax(Q-X,0)。消费者的保留价格为r,零售商对策略型消费者保留价格的预期为ξr,策略型消费者对购买到清仓期降价产品的可能性的预期为ξprob,对残值的预期为s0。理性预期均衡下,消费者在销售期购买产品的剩余和在清仓期购买产品的期望剩余是相等的,所以产品在销售期初的销售价格满足v-p=(v-s)ξprob,同时策略型消费者对购买到清仓期降价产品的可能性满足ξprob=F(Q),零售商对顾客保留价格的预期ξr=r,消费者对残值预期s0的满足s0=Es。 与2.2中的分析过程类似,此时零售商同样只会采取两种定价策略,即定价为策略型消费者的保留价格r或是对产品的估值v。销售期的价格p定在r和v之间或之外的任何地方都只会使得零售商的预期利润降低。接下来,我们主要就这两种定价策略进行分析与讨论。 如果采取估值定价策略,即把销售期价格p定在估值v上时,市场上短视型消费者会选择在销售期购买产品,而策略型消费者会选择在清仓期购买产品。此时,零售商利润函数可以表示为∏H(Q,v)=E[(v-s)(kX∧Q)-(w-s)Q]。将清仓期的价格代入上式,可以得到∏H(Q,v)=E[αMax(Q-kX,0)(kX∧Q)]-{w-v+E[αMax(Q-kX,0)]}Q。 简化得到: 对比两种定价策略下的一阶条件,可以得到: 接下来,我们进一步比较两种定价策略下,零售商的最优利润之间的大小关系。 命题3和命题4的分析表明,无论是否考虑残值的变化,只要存在顾客的异质性,当k较小时,保留价格定价策略就一定会优于估值定价策略。然而,随着k的增加,二者的差异将逐渐缩小。并且,存在一个阈值点,当k大于这一阈值点时,估值定价策略将优于保留价格定价策略。由于策略型消费者在人群中的比率越来越多,一般情况下,零售商可以不必进行策略对比而直接采用保留价格定价策略,因而保留价格定价策略是一种当前对企业更具现实意义的定价策略。 假设需求X服从正态分布N(μ,σ),μ=100,σ=25。批发价格w为100,策略型消费者对产品的估值v为350。首先我们考察基本模型中不存在数量保证与存在数量保证机制下零售商的最优策略。 图1 两种定价策略下的零售商利润函数与最优订购量 接下来考虑考虑残值是一确定值,而消费者存在异质性的情形。假设s=50,图2、图3和图4分别画出了当 k=0.8, 0.5, 0.2采用保留价格定价和估值定价时零售商的利润函数。 图2 两种定价策略下的零售商利润函数与最优订购量(k=0.8) 图3 两种定价策略下的零售商利润函数与最优订购量(k=0.5) 图4 两种定价策略下的零售商利润函数与最优订购量(k=0.2) 从图2-图4可以看出,当短视型消费者数量较多时(如k=0.8),零售商采取估值定价的方法能获得更大的利润;当短视型消费者较少时(如k=0.2),零售商采用保留定价的方法能够的更大的利润。同时,容易验证,以上三种情况均表明估值定价下最优订购量Q0和保留定价下的最优订购量QC满足Q0≥kQC,这正是命题2所描述的性质。此外,通过三个图可以看出,估值定价下的最优订购量总是小于保留价格下的最优订购量,当k越大时,两个订购量越接近。 下面进一步探讨短视型消费者的比例对问题造成的影响。短视型消费者和策略型消费者在数量上的比率为k:(1-k)。如前所述,当零售商将销售期价格p定在策略型消费者保留价格r上时,市场上所有消费者都会选择在销售期购买;零售商将p定在消费者估价v上时,短视型消费者会选择立即购买,策略型消费者只会等待在清仓期以残值的价格购买。在这两种定价策略下,零售商利润的大小均短视型消费者在市场上的占比k值有关,如图1所示,其中横坐标是短视型消费者的比率k,纵坐标是零售商的期望利润。 由图5可以看出,当零售商把销售期的价格定在消费者估值v上时,零售商的利润随短视型消费者所占比率k的增大而成正比例增大。当零售商把销售期的价格定在策略型的保留价格r上时,达到理性预期均衡的零售商利润与比率k值无关。当短视型消费者所占比率k为0.2时,定价在消费者估值v和定价在策略型消费者的保留价格r的零售商的利润是相等的。短视型消费者所占比率k<0.2时,零售商应该把销售期的价格定在策略型消费者的保留价格r上。短视型消费者所占比率k>0.2时,零售商应该把销售期的价格定在消费者估值v上。 图5 两种定价策略下的零售商期望利润与k的关系(固定残值情形) 接下来,考虑消费者存在异质性,且残值由清仓期的库存决定的情形。此时,残值是变化的,即s=p-αMax(Q-X,0),假设其中残值系数α为0.5。当零售商把销售期价格p定在策略型消费者保留价格r上时,消费者的购买行为以及零售商定价策略与2.1中讨论的市场上全部都是策略型消费者的情景是一致的。 当零售商把销售期的价格p定在消费者的估值v上时,市场上的短视型消费者会选择在销售期购买产品,而策略型消费者会选择在清仓期购买产品。由2.3的分析可知,存在唯一的订购量使得零售商的预期利润达到最大。图2展示了两种定价策略下,不同比例k的短视型消费者导致的零售商期望利润。 图6 两种定价策略下的零售商期望利润与的关系(变化残值情形) 由图6可以看出两点。第一,只有当短视型消费者的比例大于某个阈值点k0(本例该数值约为0.5)时,采用估值定价策略才能盈利。第二,存在一个阈值点k1, 当短视型消费者所占比例低于该阈值(本例该阈值在0.5与0.6之间)时,保留价格定价策略优于估值定价策略,而当短视型消费者所占比例高于该阈值时,则估值定价策略优于保留价格定价策略。 随着市场竞争的加剧,越来越多的企业采取季末降价促销或定期促销,在零售电子商务领域甚至达到了白热化,这也相应催生了越来越多的“等降价”策略型消费行为。然而,也有一部分消费者不关心未来的降价可能,只要产品价格低于自身的估值就会立即购买产品。零售商如何面对市场上存在的策略型消费者延期购买行为,如何综合考虑策略型消费者和短视型消费者行为的差异,进而进行定价与库存决策,成为当前学术界与企业共同关心的热点问题。与此同时,在当今市场上,零售商为使得自身的预期利润最大,往往在销售期末会根据剩余库存量来降价抛售,这一促销策略又将如何影响消费者的购买选择行为,进而影响零售商的决策及其绩效,则是企业必须面对的问题。本文在考虑以上因素的前提下对消费者的购买选择行为以及消费者与零售商的博弈过程进行了模型分析,并对决策均衡解的性质进行了讨论,为零售商的定价与库存决策提供了参考。如前所述,在Su Xuanming和Zhang Dan[1]的开拓性研究之后,基于策略型消费者的定价与库存问题在最近几年已经引致了广泛的关注和一系列后续研究[2-5,12-24],本文的研究则综合考虑了残值变化和顾客类型的异质性,使得这一领域的相关研究结论更具解释力和现实意义。 本文的分析表明,在消费者均为策略型消费者,且清楚零售商将采取残值定价策略的情况下,零售商可以通过数量保证策略来提高自身的期望利润,同时降低库存订货量。Su Xuanming和Zhang Dan[1]的研究考虑了数量保证策略,但是未考虑残值的变化,本文的这一研究结论进一步增强了对这一问题的解释力。本文的分析还表明,在考虑顾客异质性的条件下,零售商可以采取保留价格定价和估值定价两种定价策略。当采取估值定价策略时,零售商的最大期望利润与短视型消费者在市场上的比例成正相关,并且存在唯一的短视型消费者在市场上的占比值使得定价在保留价格时的利润和定价在消费者估值时所达到最高利润相等。由于现代社会中的消费者越来越精明,策略型消费者在人群中的比率越来越多,一般情况下,零售商甚至可以不必进行策略对比而直接采用保留价格定价策略。因而,这一研究结论对企业颇具现实意义,有助于企业战略性地选择适宜的定价策略。 [1] Su Xuanming, Zhang Fuqiang. Strategic customer behavior, commitment, and supply chain performance[J]. Management Science, 2008, 54(10): 1759-1773. [2] Su Xuanming, Zhang Fuqing. On the value of commitment and availability guarantees when selling to strategic consumers[J]. Management Science, 2009, 55(5): 713-726. [3] Jerath K, Netessine S, Veeraraghavan S K, Revenue management with strategic customers: Last-minute selling and opaque selling[J]. Management Science, 2010, 56(3): 430-448. [4] Cachon G P, Swinney R. Purchasing, pricing, and quick response in the presence of strategic consumers[J]. Management Science, 2009, 55(3): 497-511. [5] Cachon G P, Swinney R. The value of fast fashion: Quick response, enhanced design, and strategic consumer behavior[J]. Management Science, 2011, 57(4): 778-795. [6] Coase R H. Duability and monopoly[J]. Journal of Law and Economics, 1972, 15(1):143-149. [7] Conlisk J, Gerstner E, Sobel J. Cyclic pricing by a durable goods monopolist[J]. Quarterly Journal of Economics, 1984, 99(3):489-505. [8] Besanko D, Winston W L. Optimal prize skimming by a monopolist fading rational consumers[J]. Management Science, 1990, 21(36): 555-567. [9] Talluri K, van Ryzin G.Revenue management under a general discrete choice model of consumer behavior[J]. Management Science, 2004, 50 (1):19-33. [10] Zhang Dan, Cooper W L. Managing clearance sales in the presence of strategic customers[J]. Production and Operations Management, 2008, 17(4): 416-431. [11] Aviv Y, Pazgal A. Optimal pricing of seasonal products in the presence of forward-looking consumers[J]. Manufacturing & Service Operations Management, 2008,10(3): 339-359. [12] Lai Guoming, Debo L G, Sycara K. Buy now and match later: Impact of posterior price matching on profit with strategic consumers[J]. Manufacturing & Service Operations Management, 2009, 12(1): 33-55. [13] Osadchiy N, Vulcano G. Selling with binding reservations in the presence of strategic consumers[J].Management Science, 2010, 56(12): 2173-2190. [14] Mersereau A J, Zhang Dan. Markdown pricing with unknown fraction of strategic customers[J]. Manufacturing & Service Operations Management, 2012, 14(3): 355-370. [15] Liu Qian, Zhang Dan. Dynamic pricing competition with strategic customers under vertical product differentiation[J]. Management Science, 2013, 59(1): 84-101. [16] Li Cuihong, Zhang Fuqing. Advance demand information, price discrimination, and preorder strategies[J]. Manufacturing & Service Operations Management, 2013, 15(1): 57-71. [17] 刘晓峰,黄沛.基于策略型消费者的最优动态定价与库存决策[J].管理科学学报, 2009,12(5): 18-28. [18] 黄松,杨超,张曦.考虑战略顾客行为带预算约束的多产品报童问题[J].中国管理科学,2011,19(3):70-78. [19] 刘晓峰,徐贤浩.消费者策略行为视角下短生命周期产品的定价机制研究[J].中国管理科学,2011,19(4):152-158. [20] 李贺,张玉林,仲伟俊.考虑战略消费者行为风险的动态定价策略[J].管理科学学报, 2012, 15(10):11-25. [21] 李贺,张玉林. 考虑顾客行为和风险因素的定价及配给研究[J].管理工程学报, 2014, 28(2):151-159. [22] Whang S. Demand uncertainty and the bayesian effect in markdown pricing with strategic customers[J]. Manufacturing & Service Operations Management, 2014,17(1):66-77. [23] Levin Y, McGill J, Nediak M. Dynamic pricing in the presence of strategic consumers and oligopolistic competition[J]. Management Science, 2009,55(1): 32-46. [24] Gönsch J, Klein R, Neugebauer M, et al. Dynamic pricing with strategic customers[J]. Journal of Business Economics, 2013, 83(5):505-549. [25] Caro F, Gallien J. Clearance pricing optimization for a Fast-Fashion retailer[J]. Operations Research, 60(6):1404-1422. Pricing and Inventory Decisions with Inventory-Dependent Salvage Value, Strategic Consumer Behavior, and Customer Heterogeneity WANG Xia-yang, FU Ke, YU Bin (Lingnan(University) College, Sun Yat-sen University, Guangzhou, 510275, China) In this paper, the impacts of strategic consumer behavior on a retailer’s pricing and inventory decisions are studied. Most of the literature on strategic consumer assumes that consumers are all strategic and the salvage value is a constant. The joint effect of heterogeneity of consumer type and inventory-dependent salvage value under the general framework of strategic consumer behavior are considered. In particular, the salvage value depends on leftover inventory at the end of a selling season. The rational expectations equilibrium in the base model is characterized and the model with the considerations of quantity commitment, inventory-dependent salvage value, and customer heterogeneity is extended. When consumers are all strategic and are aware of how the product is salvaged, the retailer’s expected profit can be improved and inventory can be decreased with quantity commitment are shown. When consumers are heterogeneous, the retailer can use two pricing strategies, i.e. reservation price and valuation price. The retailer’s maximum expected profit will positively relate to the ratio of myopic consumers to all consumers when it employs valuation price strategy. Moreover, there exists a threshold ratio, above which the valuation price strategy dominates the reservation price strategy, and vice versa. Our study provides several new managerial insights on how firms could optimize their profits when faced with strategic consumers. strategic consumer behavior;rational expectations equilibrium; inventory-dependent salvage value;consumer heterogeneity 1003-207(2016)01-0097-10 10.16381/j.cnki.issn1003-207x.2016.01.012 2013-12-29; 2015-01-28 国家自然科学基金资助项目(71102101, 71472191, 71072090,71222105) 简介:傅科(1975-),男(汉族),四川绵竹人,中山大学岭南学院物流工程与管理系教授,博士生导师,研究方向:运作与供应链管理,E-mail:fuke@mail.sysu.edu.cn. C934 A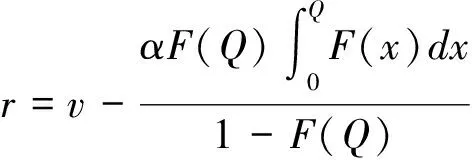
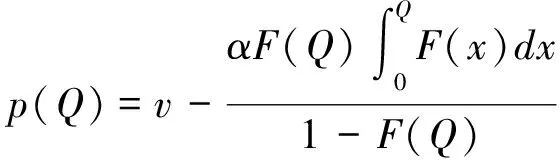
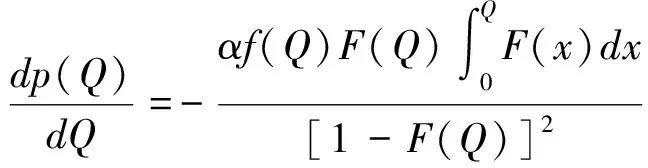
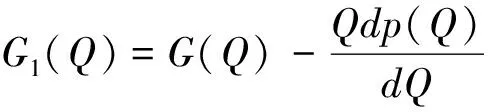
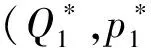
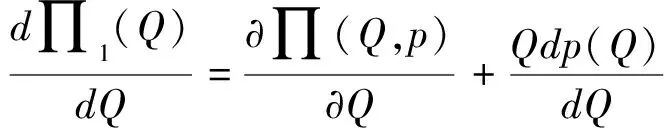
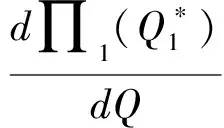
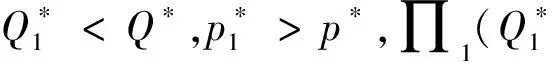
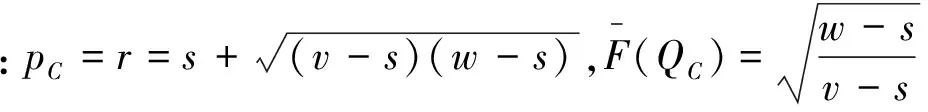
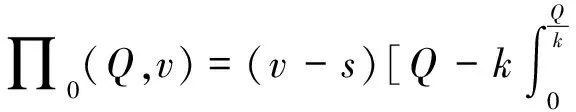
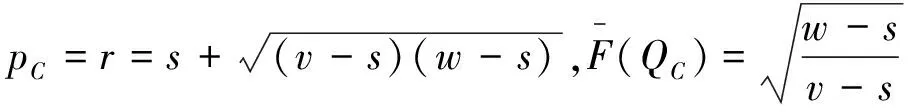
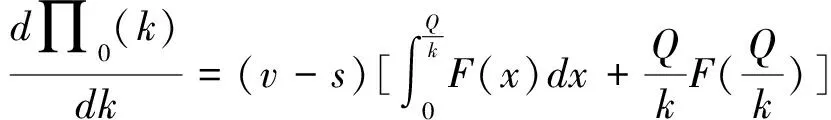
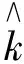
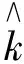
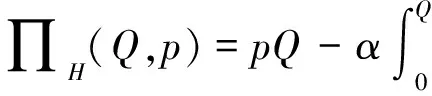
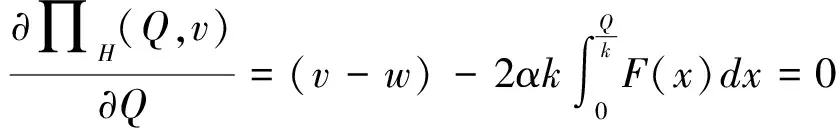
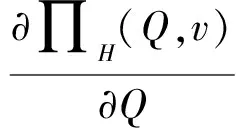
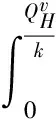
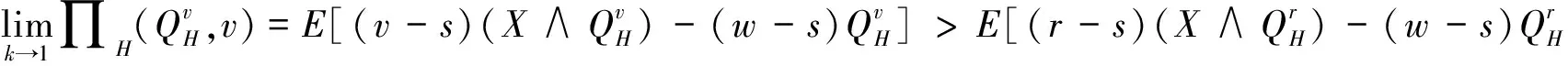
3 算例讨论
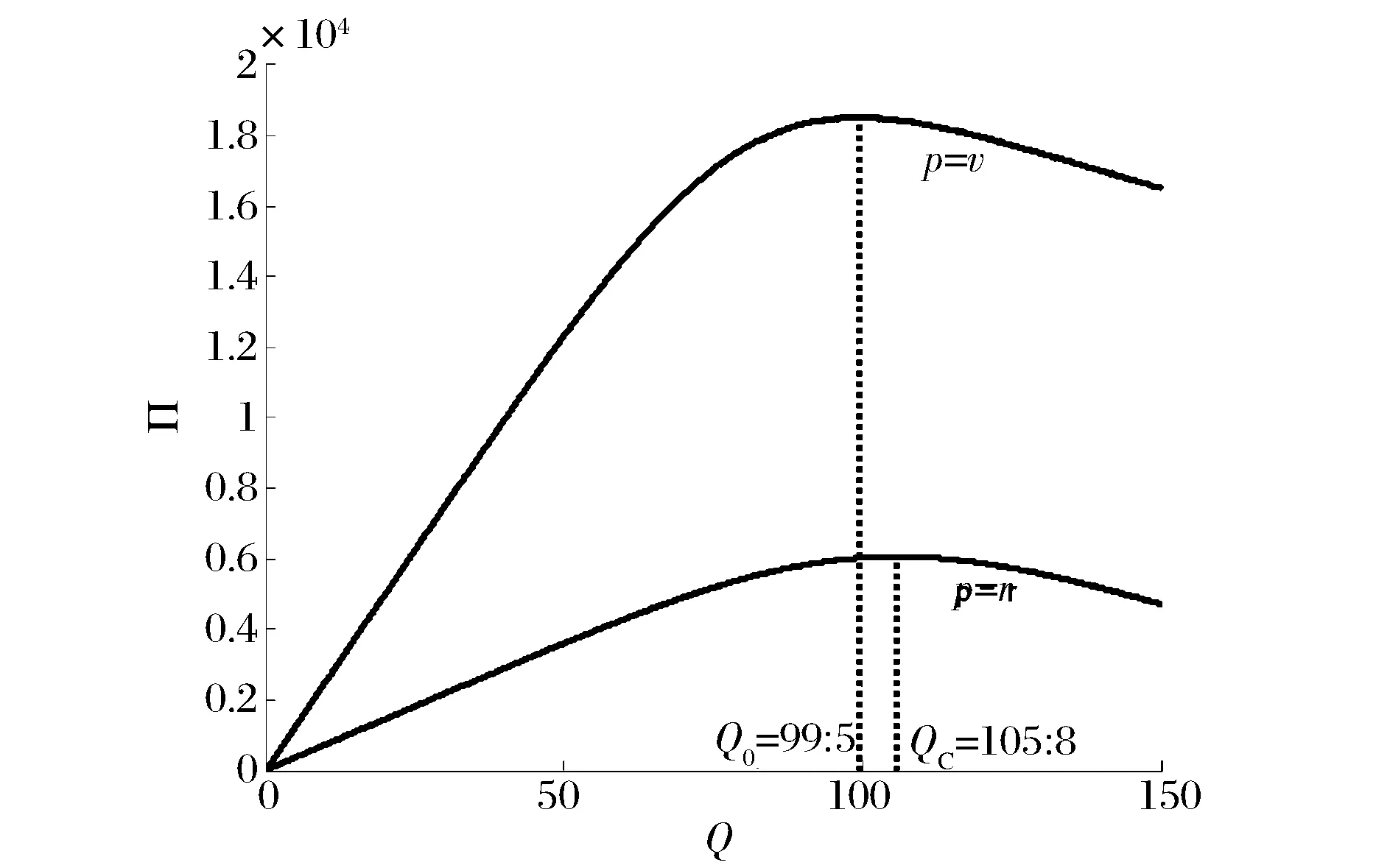
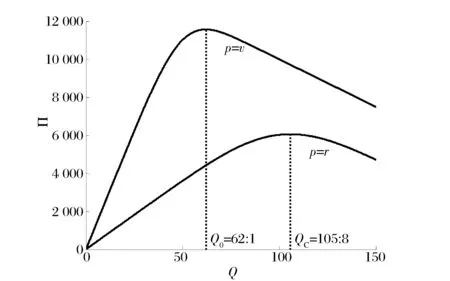
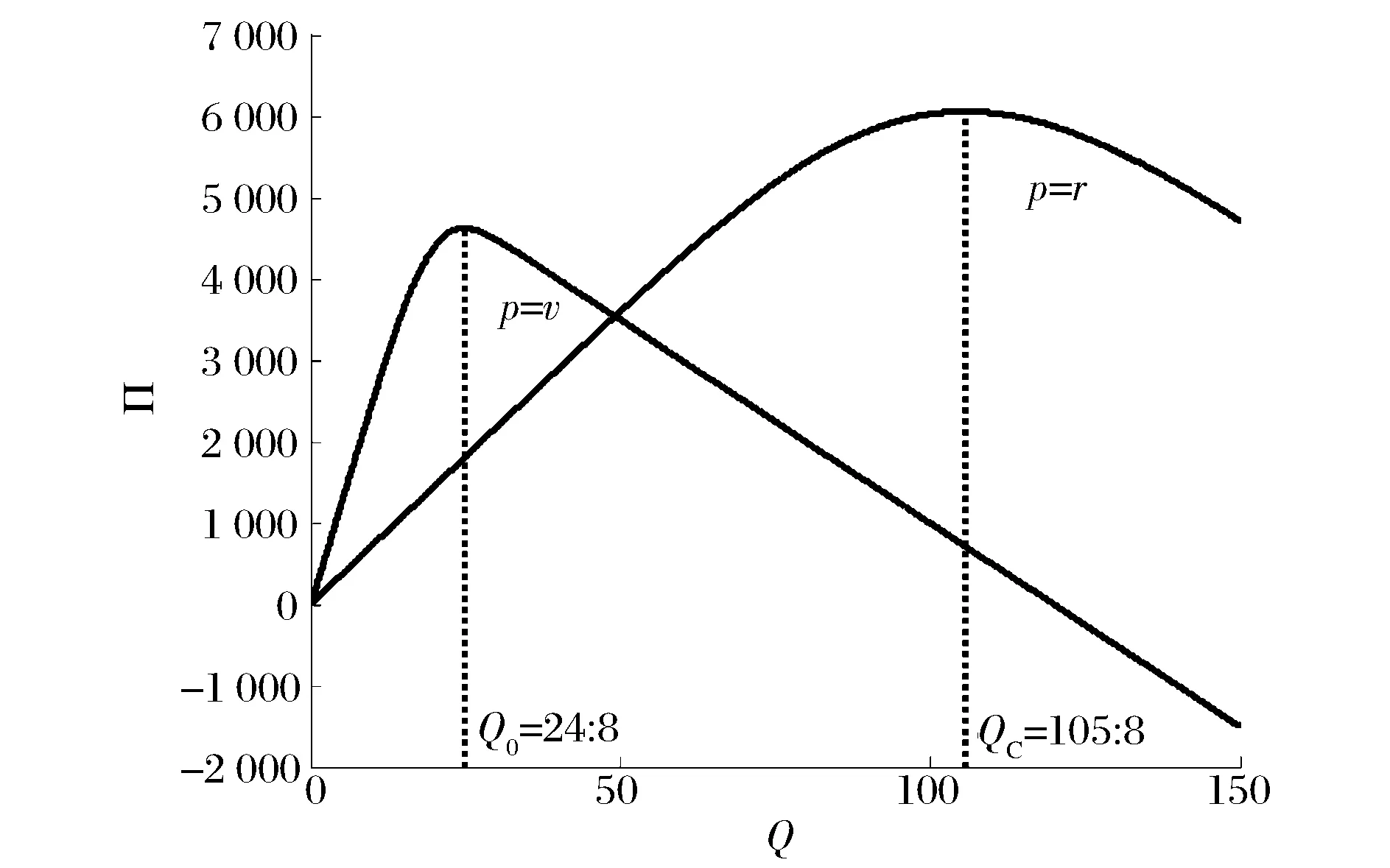
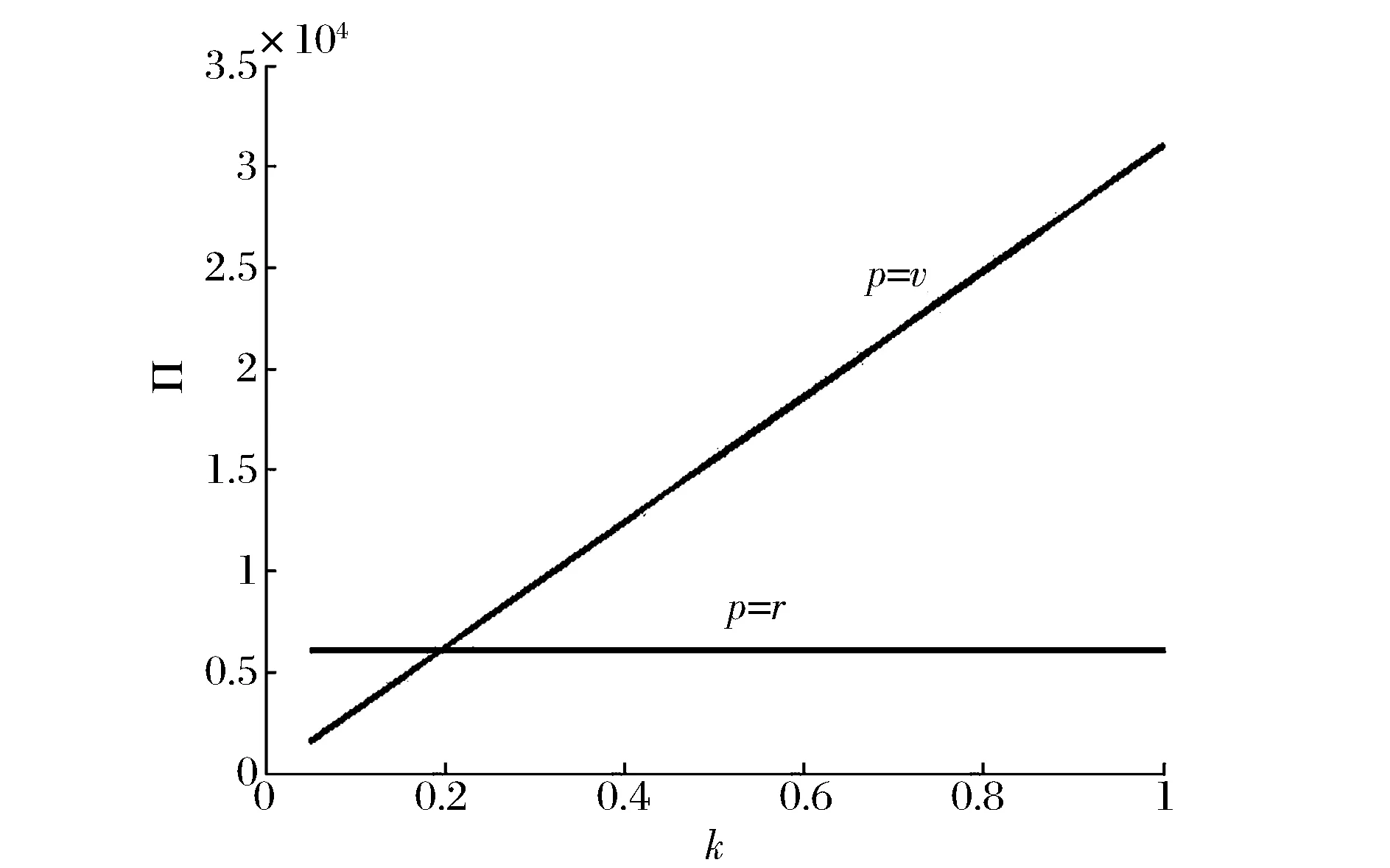
4 结语
