供应链式产业集群技术创新博弈分析

王丽丽，陈国宏

(福州大学经济与管理学院，福建 福州 350116)



供应链式产业集群技术创新博弈分析

王丽丽，陈国宏

(福州大学经济与管理学院，福建 福州 350116)

供应链式产业集群具备集群和供应链特性，这类集群的技术创新活动存在两种类型：供应链上下游企业创新活动和供应链间企业创新活动。从技术创新视角出发，将集群创新过程分成研发阶段和产出阶段，并引入技术溢出系数、研发资金、技术创新成功概率等变量，用动态博弈方法分别对供应链上下游企业及供应链间企业的技术创新进行分析，推导出企业利润均衡函数，最后得出如下结论：①供应链上下游企业不创新或同时创新的情况下，双方将共享利润；②由于存在技术溢出现象，供应链内某一企业进行创新，该企业及其上下游企业利润都将提高；③供应链内上下游企业采取合作创新的利润大于未创新和独立创新情况下的利润；④供应链核心企业间的竞争激烈，链间技术溢出程度变小，不创新的企业市场份额将降低，利润减少。

供应链式产业集群；技术创新；博弈

1 引言

近年来，国内外具有供应链特征的产业集群客观存在，如美国硅谷的微电子产业集群、德国索林根的刀具产业集群、福建东南汽车产业集群、广东顺德家电产业集群。供应链和产业集群发展存在密切的内在联系，这有利于产业集群升级及企业核心竞争力提高，产业集群为供应链的发展提供天然平台，供应链的形成又能促进集群整体升级，二者之间的相互耦合使集群内企业的专业分工更加明确、效率提高，逐渐形成新的经济组织范式——供应链式产业集群(链式集群)，有学者把这类经济组织范式称作“集群供应链”[1]，但二者的研究侧重点不同。“集群供应链”侧重于供应链，强调供应链企业的本地一体化，关注企业间的协作关系；但是供应链式集群侧重于产业集群，强调集群的网络性和复杂性，关注纵向企业相互分工协作、横向企业相互竞争协调的关系。链式产业集群是指在特定集群地理区域内，各类型企业、研发机构、中介服务机构等组织以供应链为主导关系，纵向企业相互分工协作高度发达，横向企业相互竞争协调，形成的“聚集性产业，专业化经营，网络化协作，高效性竞争，紧密型关联”的网络组织[2]。从博弈论角度看，集群内企业的创新活动可以视为是否采用创新技术的决策行为，由于链式集群存在供应链特性，因此在这类集群存在两类创新博弈活动——供应链上下游企业间创新博弈行为和供应链间创新博弈行为。

目前，众多学者[3-9]已运用经济学和博弈论的方法对供应链和产业集群的技术创新问题进行研究，思路大多将成本与收益关系融入技术创新理论建立多阶段寡头博弈模型。由于链式集群的现象普遍存在，近年来，一些学者从集群的供应链网络性角度研究企业的创新博弈行为，如：黎继子[10]引入资金时间价值以及合作约束条件，分析产业集群两核心企业动态博弈行为；蔡猷花[11]在集群环境中考虑创新投入因素，建立供应链链间企业的博弈模型；左志平[12]运用演化博弈理论，分析了集群供应链横向和纵向两个不同维度的技术创新行为的博弈均衡结果；徐玲玲，刘春玲[13]在集群式供应链中引入拥挤效应和知识溢出，分析距离对集群内核心企业决策的影响。结合企业创新实践发现，技术溢出程度和创新成功概率是企业决定是否创新的重要因素，但他们均未考虑技术创新成功率对企业创新博弈的影响，黎继子等[10-12]未考虑技术溢出对创新博弈的影响。本研究在蔡猷花、黎继子等人研究基础上，将供应链式产业集群企业的技术创新决策过程分为研发阶段和产出阶段，以供应链网络特征为基础，考虑技术溢出、创新成功率、研发投入等因素，运用完全信息动态博弈理论分析链式集群中链内和链间企业的创新行为。首先从微观角度，以产品价格或加价为决策内容，分析集群中单链供应链上下游企业创新博弈竞合问题；其次从中观角度，以产量为决策内容，分析并行供应链核心企业创新博弈竞合问题，这将进一步完善供应链式集群的理论体系。

2 供应链内上下游企业创新博弈分析

2.1 模型假设

为了研究方便，将供应链内的企业简单地分为上游企业和下游企业，分别记作企业1和企业2，它们彼此了解，模型的相关假设如下：

假设1：技术创新决策过程分为两个阶段：研发阶段和产出阶段。在研发阶段，企业有不同的策略(合作研发、非合作研发)，而在产出阶段，上游企业的决策内容为产品的价格，下游企业的决策内容是销售价格(或相对于原材料价格的加价)。

假设2：供应链内两企业的产品初始单位成本不同，倘若技术创新成功能够降低产品单位成本；

假设3：在供应链式产业集群中，上下游企业间存在技术溢出，技术溢出程度由技术溢出系数决定，由于供应链式产业集群具有供应链和产业集群的双重特性，因此与传统集群相比，企业间的联系与互动更加频繁，技术溢出系数更大些；

假设4：需求函数、技术溢出系数和单位成本等都是双方的共同知识；

假设5：在研发阶段，上下游企业间不了解对方的创新策略，同时决策；

假设6：上下游企业按照订单生产，在产出阶段，上下游企业同时决定价格或加价；

假设7：不同企业进行技术创新需投入等额的研发资金。

2.2 模型建立

考虑两阶段博弈，第一阶段为研发阶段，在该阶段上下游企业同时选择合作创新或非合作创新,且非合作创新分为自主创新和不创新两种情形，不同的选择对应不同的研发投入yi；第二阶段为产出阶段，上下游企业按照订单生产，同时决定价格或加价pi，因此整个过程是两阶段完全信息动态博弈，均衡结果是一个子博弈纳什均衡，可以采用逆向归纳法求解。

(1)经济学理论认为一般产品的线性需求函数为Q=a-bP。从供应链角度看，上游企业为下游企业提供原材料，设p1为上游企业的产品价格；下游企业对上游企业提供的原材料进行加工、处理或组装，下游产品在上游产品基础上产生了增值(或称加价)设为p2。假设1个单位下游产品需γ单位上游产品，则下游企业的价格为γp1+p2；设q1为上游企业的产量，q2为下游企业的产量。由假设6可知上游企业按照下游企业的订单生产，所以q1=γq2。由一般需求函数得下游企业需求函数为q2=a-b(γp1+p2)，则上游企业需求函数为q1=γ[a-b(γp1+p2)]。

(2)供应链内上下游企业的单位成本为Ci，初始单位成本为C0i，创新成功后单位成本函数为：

Ci=C0i-Xi-βXj(i,j=1或2，i≠j)其中，β∈[0,1]表示企业间的技术溢出系数，该系数由供应链式产业集群内的企业间协调和沟通能力、知识传播能力、供应链长度、平均路径长、网络聚集系数和网络度分布等决定。Xi表示企业技术创新对单位生产成本下降的贡献，βXj表示其他企业技术创新对该企业生产成本下降的贡献。这里还有一个特殊情况，上下游企业采取合作创新的方式，则β=1。

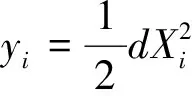
(4)技术创新成功的概率为θi，则失败的概率为1-θi。根据假设2的创新成功后的单位成本函数，可得创新的期望单位成本函数：

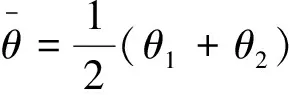
根据以上假设可得，上下游企业利润为：

2.3 模型求解及分析

2.3.1 产出阶段博弈均衡分析

考虑第二阶段均衡价格或加价水平。由模型假设6可得，在产出阶段，上下游企业按照订单生产，同时决定价格或加价pi，使自己的收益最大化，因此对pi求偏导：

解得：

2.3.2 研发阶段博弈均衡分析

根据是否进行合作可将研发阶段策略分为合作研发和不合作研发。不合作研发是指给定其他企业的研发投入企业自主选择研发投入水平(当为0时，表明企业选择不研发)，以最大化自己的利润。合作研发是指企业之间共同承担研发的投入[5]。研发阶段策略矩阵见表1-1。

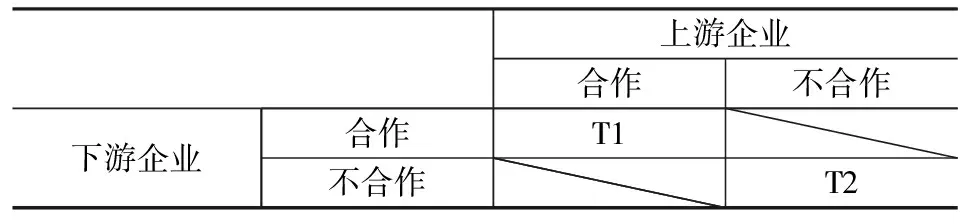
表1-1

因为合作研发只有双方均选择合作才有可能实现，因此(不合作，合作)和(合作，不合作)为不可能实现的策略。并且不合作研发策略又可以分为自主研发和不研发，因此T2=(不合作，不合作)可以用子策略矩阵表1-2表示。

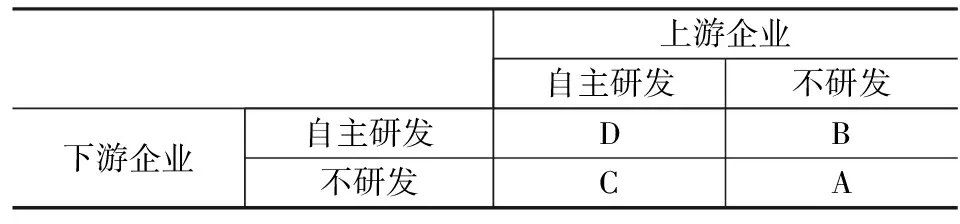
表1-2

2.3.2.1 企业不合作时的博弈均衡分析

设该创新技术需要研发投入为M。上下游企业不合作时，可能出现四种情况：A：上下游企业均不研发(y1=y2=0)；B：上游企业不研发(y1=0)，下游企业自主研发(y2=M)；C：上游企业自主研发(y1=M)，下游企业不研发(y2=0)；D：上下游企业都自主研发(y1=y2=M)。下面分别讨论四种情况下，上下游企业的最大利润。

①上下游企业均不研发(y1=y2=0)

经计算得，上下游企业最大利润为：

结论1：供应链式产业集群内，供应链内上下游企业获利行为是联动机制，在双方不创新的情况下，双方将共享利润。

②上游企业不研发(y1=0)，下游企业自主研发(y2=M)

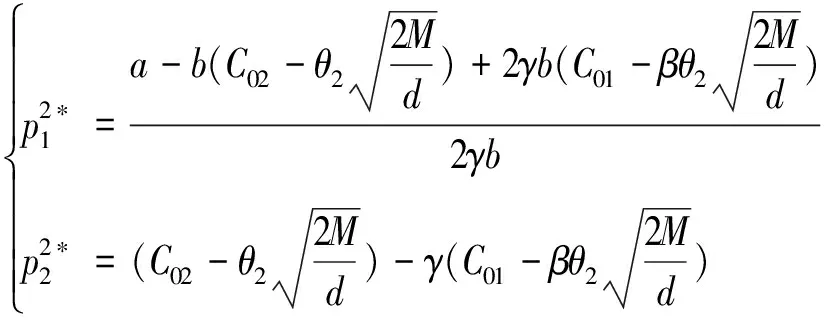
经计算得，上下游企业最大利润为：

结论2：供应链式产业集群中，在下游企业采用新技术的情况下，无论是否存在技术溢出现象，上游企业都能提高利润。这是由于下游企业采用创新技术使得相对产品成本下降，生产量增加，需要购买更多的原材料，而上下游企业是按订单生产，因此相应的上游企业销售量增加，利润提高。

③上游企业自主研发(y1=M)，下游企业不研发(y2=0)

经计算得，上下游企业最大利润为：

结论3：在供应链式产业集群中，当上游企业采用新技术的情况下，由于存在技术溢出现象(即β>0)，下游企业的利润也相应提高(即此时下游企业利润大于双方未创新时的利润)。这是由于上游企业采用创新技术，产品相对成本下降，下游企业从上游企业购买原材料的价格也相应下降，下游企业利润提高；而此时上游企业需多投入研发费用，因此采用创新的上游企业利润反而小于下游企业。学者们把这种现象称为“搭便车”。

北京兰台律师事务所税法律师武嘉认为，逃避缴纳税款的纳税人需要承担行政责任，补交税款、滞纳金和罚款。如果在刑事立案前如数补交税款、滞纳金、罚款的，可能不予追究刑事责任，结果或许没有想象那么坏。

④上下游企业都自主研发(y1=y2=M)

经计算得，上下游企业最大利润为：

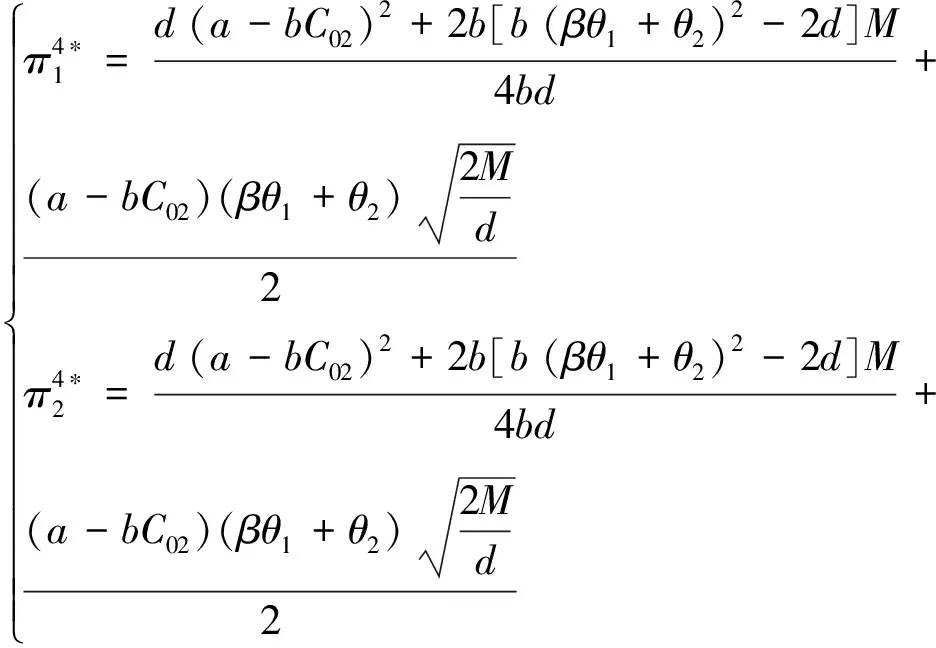
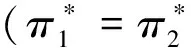
2.3.2.2 企业合作时的博弈均衡分析

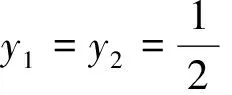
经计算得，此时上下游企业的利润为：

结论5：在供应链式产业集群中，供应链内上下游企业采取合作创新的形式，双方研发投入将减半、共享创新技术、平分创新利润，且此时利润大于未创新的情况。

3 供应链间创新博弈分析

在供应链式产业集群内，企业之间的竞合关系往往表现为供应链与供应链之间的竞争与合作，而供应链的主导力量在于核心企业，因此可以通过分析核心企业的技术创新博弈行为，从微观角度研究供应链间技术创新扩散活动。

3.1 模型假设

为了研究方便，本研究以双核型(两个核心企业)供应链式产业集群为例分析供应链间创新博弈行为。简单地将两条供应链记为供应链1和供应链2，模型的相关假设如下：

假设1：在供应链式产业集群中，两核心企业处于双寡头市场，两条供应链地位相等，技术实力相当；

假设2：技术创新决策过程分为两个阶段：研发阶段和产出阶段。在研发阶段，核心企业有不同的策略：合作研发或非合作研发，而在产出阶段，企业的决策内容是产量；

假设3：核心企业是同行企业且产品无差异，初始单位成本相同，倘若技术创新成功能够降低产品单位成本；

假设4：在供应链式产业集群中，供应链间存在技术溢出，技术溢出程度由技术溢出系数决定；

假设5：需求函数、技术溢出系数和成本等都是双方的共同知识；

假设6：在研发和产出阶段，核心企业间不了解对方的创新策略，同时决策；

假设7：不同企业进行技术创新需投入等额的研发金额。

3.2 模型建立

考虑两阶段博弈，在第一阶段为研发阶段，核心企业(代表供应链)同时选择合作研发或非合作研发,且非合作研发分为自主研发和不研发，不同的选择对应不同的研发投入yi；在第二阶段为产出阶段，核心企业同时决定产量，因此整个过程是两阶段完全信息动态博弈，均衡结果是一个子博弈纳什均衡，可以采用逆向归纳法求解。

(1)设供应链式产业集群的两核心企业处于双寡头市场，qi为各自的产量。则产品需求函数为P=a-b(q1+q2)。

(2)核心企业产品的初始单位成本为C0，创新成功后单位成本函数为：

Ci=C0-Xi-βXj(i,j=1或2，i≠j)

其中，β∈[0,1]表示企业间的技术溢出系数，该系数由供应链式产业集群内的企业间协调和沟通能力、知识传播能力、供应链长度、平均路径长、网络聚集系数和网络度分布等决定。Xi表示企业技术创新对单位生产成本下降的贡献(即创新效益)，βXj表示其他企业技术创新对该企业单位生产成本下降的贡献。这里还有一个特殊情况，核心企业间采取合作创新的方式，则此时β=1。

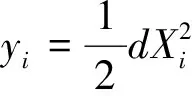
(4)技术创新成功的概率为θi，则失败的概率为1-θi。则根据假设2的创新成功后的单位成本函数，可得创新的期望单位成本函数：

E(Ci)=C0-θiXi-θjβXj(i,j=1或2，i≠j)

根据以上假设可得，两核心企业利润为：

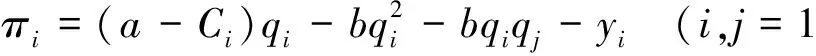
3.3 模型求解及分析

3.3.1 产出阶段博弈均衡分析

考虑产出阶段均衡时各核心企业的产量，核心企业能够决定产量，以获取最大利润，因此对qi求偏导。

解得：

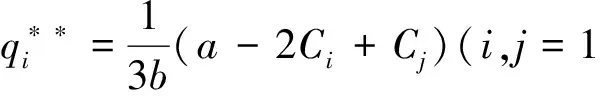
根据是否进行合作可将研发阶段分为合作研发和不合作研发。则研发阶段策略矩阵见表1-3。

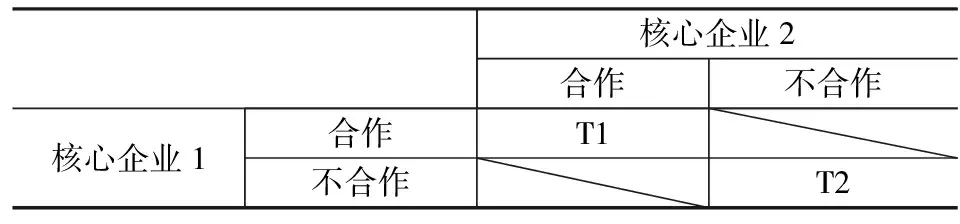
表1-3

因为合作研发只有双方均选择合作才有可能实现，因此(不合作，合作)和(合作，不合作)不可能实现策略。并且不合作研发策略又可以分为自主研发和不研发，因此T2=(不合作，不合作)可以用子策略矩阵表1-4表示。

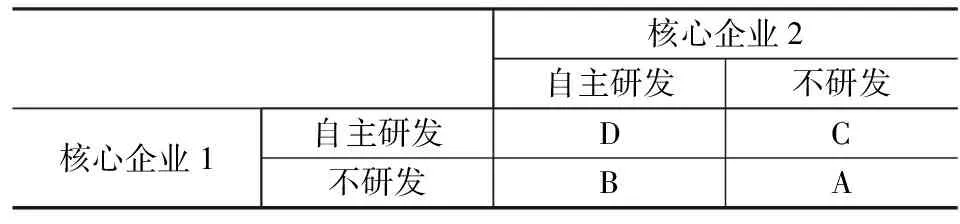
表1-4

3.3.2.1 企业不合作时的博弈均衡分析

设该创新技术需要研发投入为M。两核心企业不进行合作时，可能出现四种情况：A：两核心企业都不研发(y1=y2=0)；B：核心企业1不研发(y1=0)，核心企业2自主研发(y2=M)；C：两核心企业都自主研发(y1=y2=M)；D：核心企业1自主研发(y1=M)，核心企业2不研发(y2=0)。但由于两核心企业地位相同，因此B和C属于同一情况。下面分别讨论三种情况下，各核心企业的最大利润。

①核心企业均不研发(y1=y2=0)

经计算得，两核心企业最大利润为：

结论6：在供应链式产业集群中，核心企业地位相同，在均未创新的情况下，双方将共享利润。

②核心企业1自主研发(y1=M)，核心企业2不研发(y2=0)

经计算得，两核心企业的最大利润为：

通过计算得：

当β=1时，

当β=0时，

结论7：一般情况下，供应链式产业集群中，当竞争对手创新，而企业自身不创新的情况下，企业的市场份额降低，利润减少。这是由于核心企业之间的竞争相当激烈，创新企业将采取各种保护措施，尽可能减少技术溢出现象，从而当技术溢出系数β比较小(β<0.5)时，未创新企业难以通过“搭便车”共享创新企业的成果。

③核心企业都自主研发(y1=y2=M)

经计算得，两核心企业最大利润为：

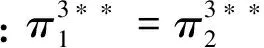
结论8：在供应链式产业集群中，两供应链的核心企业都创新，成本下降，产量提高，利润增加。

3.3.2.2 企业合作时的博弈均衡分析

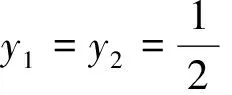
经计算得，两核心企业的利润函数为：

结论9：供应链式产业集群中，两供应链核心企业采取合作创新的形式，双方研发投入减半、共享创新技术、平分创新利润。

4 结语

本文在供应链式集群网络特征分析的基础上，运用动态博弈求解方法，推导出在合作与非合作情况下集群内供应链上下游企业及链间核心企业技术创新博弈均衡条件，并得出结论，这些结论是对以往研究的补充与扩展：①在供应链式产业集群中，供应链上下游企业不创新或同时创新的情况下，双方将共享利润；②由于存在技术溢出现象，供应链内某一企业进行创新，企业及其上下游企业利润都将提高，且大于未创新情况下的利润，这也是产业集群技术创新“搭便车”现象原因之一；③在不合作情况下，供应链内上下游企业均采取自主创新的情况下，双方利润小于未创新时的利润，而在企业采取合作创新的情况下，双方利润大于未创新的情况；④在供应链式产业集群中，供应链核心企业间的竞争激烈，链间技术溢出程度小，不创新的企业市场份额降低，利润减少。

[1] 黎继子，蔡根女，卢德银.基于集群网络式供应链变迁演化规律研究[J].情报杂志，2004，23(2)：4-6.

[2] 蔡彬清，陈国宏. 复杂网络视角下链式产业集群竞争优势分析——以柳市低压电器产业集群为例[J].经济地理，2012，32(10)：83-88.

[3] Cachon G，Zipkin P H.Competitive and cooperative inventory policies in a two-stage supply chain [J].Management Science，1999，45(7):180-191.

[4] Slikker M，Fransoo J，Wouters M. Cooperation between multiple mews-vendors with transshipments [J].European Journal of Operational Research， 2005，167(2):212-225.

[5] 戚桂清，杨锡怀，李森.基于重复博弈的集群网络供应链竞合关系分析[J].东北大学学报(自然科学版)，2006，27(2)：233-239.

[6] 党兴华，郑登攀.技术溢出情况下企业创新模式选择的非对称博弈模型研究[J].科技进步与对策，2007，24(10)：100-102.

[7] 邓卫华，易明，蔡根女.供应链成员信息共享技术策略博弈分析[J].中国管理科学，2009，17(4)：103-108.

[8] 万谦.基于简化利润函数的伯川德博弈模型的技术创新扩散讨论[J].科技进步与对策，2005,(11)：100-102.

[9] 杨建君，聂菁.双寡头企业技术创新策略的博弈分析[J].软科学，2009，23(10):59-64.

[10] 黎继子，刘春玲，蔡根女.集群式供应链的链间动态博弈合作决策分析[J].管理工程学报，2006，20(4)：20-24.

[11] 蔡猷花，陈国宏，向小东.集群供应链链间技术创新博弈分析[J].中国管理科学，2010，18(1):72-77.

[12] 左志平，黄纯辉，夏军.基于两维的集群供应链技术创新行为演化分析[J].工业技术经济，2013(1)：83-89.

[13] 徐玲玲，刘春玲，刘金.基于拥挤效应和知识溢出下集群式供应链链间博弈分析[J].物流科技，2013(3)：5-8.

A Game Analysis on the Technology Innovation of Chain-style Industrial Cluster

WANG Li-li, CHEN Guo-hong

(School of Economics and Management, Fuzhou University, Fuzhou 350116,China)

Chain-style industrial cluster has characteristics of cluster and supply chain, so technology innovation activities of enterprises happen inside and outside the supply chain. From the perspective of technological innovation, the process of cluster’s innovation activity was divided into the R&D stage and the output stage, and the coefficients of technology spillover, R&D funds, and technological innovation success probability were put in the game model. Then, dynamic game method was applied to analyze the enterprise's technological innovation inside and outside the supply chain for deducing the enterprises’ profit equilibrium function. Finally, the following conclusions:(1)In the supply chain, when whatever upstream and downstream enterprises innovate or not innovate, both of them will share the profits.(2)Due to the presence of technology overflow phenomenon in the supply chain, when some enterprises innovate, they and their upstream and downstream enterprises will increase profits.(3)In the supply chain, the profits of upstream and downstream enterprises who had innovated cooperatively are more than the ones who were out of innovation or innovation independently.(4)With the core enterprises of the supply chain competing more, the degree of technology spillover will be smaller, the market share of enterprises who had not innovated will decline, and the profit of them will reduce.

chain-style industrial cluster; technology innovation; game

1003-207(2016)01-0151-08

10.16381/j.cnki.issn1003-207x.2016.01.018

2014-06-23；

2014-10-23

国家自然科学基金资助项目(70973022,71403052,71403055)；高等学校博士学科点科研基金(20123514110011);国家社会科学基金后期资助项目(15FGL005)；福建省软科学项目(2015R0002)；福建省高校新世纪优秀人才计划项目(闽教科2015[54]号)；中国博士后科学基金(2015M570155)

简介：陈国宏(1953-)，男(汉族)，福建福州人，福州大学经济与管理学院教授，博士生导师，研究方向：技术经济与科技管理，E-mail:cgh@fzu.edu.cn.

F273.1

A