三跨斜交连续梁应力变化率的分析
2016-12-16刘亮
刘亮
(上海市政工程设计研究总院(集团)有限公司,上海市 200092)
三跨斜交连续梁应力变化率的分析
刘亮
(上海市政工程设计研究总院(集团)有限公司,上海市 200092)
利用有限元软件建立不同斜度下的连续梁模型,计算三跨连续梁跨中位置的应力,可以得到连续梁在斜度不同的情况下应力变化的规律,尤其是双室箱梁顶板和底板的变化是最为显著的。分析可以得到结论:集中力下,斜度越大,应力变化率越小;斜度对翼缘板上的应力变化率影响显著;斜度较小时,应力变化率较小,斜度较大时,应力变化率较大。
连续梁;斜交;应力;变化率
0 引 言
随着我国国民经济持续稳定的增长和综合国力的增强,带动了高等级公路及城市立体交通的全面发展。线路的高标准要求与周围场地条件的冲突,引发了各种不规则支撑桥梁结构的出现。针对这种特殊支撑体系的桥梁结构,寻求有效、实用的分析方法和构造处理措施,是桥梁工程关注的新课题。斜梁桥最显著的特点是内力弯扭耦合作用,导致跨中弯矩折减,这使得同等跨度的斜梁桥比正梁桥的纵向弯矩要小,而扭矩比正桥大。因此,斜支撑箱梁的应力有内在的分布规律,随着角度的不同,应力也不同,在同样的位置,正交箱梁在一定荷载下是一个定值。
到目前为止,正桥理论已发展得非常完善,而斜支撑桥的理论体系尚未形成。以往的研究大部分都是分散而零碎的,无论是理论解析或是数值解析都处在研究阶段,尚未能提出作为设计计算的确定方法。国内在该方面也有相关的研究[1-10]。从理论上来讲,斜支撑最显著的特点是内力弯扭耦合作用,导致跨中弯矩折减,这使得同等跨度的斜梁桥的纵向弯矩要小,而扭矩比正桥大。用理论方法来计算相应截面的应力时比较繁琐困难,而计算机模拟斜支撑桥的受力特点可以使问题在一定程度上简化,而且数据模拟良好,有助于解决现实问题。本文针对三跨连续箱梁的有机玻璃模型,利用大型分析软件ANSYS中的SHELL63单元建立模型,分析在不同斜交角情况下,跨中应力的变化情况,用斜交情况下与正交情况下应力的比值来反映此变化情况。
1 斜角系数的引进及模型的建立
1.1斜角系数的定义
支撑边(或支座连线)与桥轴线法线之间的小于90°的夹角称为斜交角,用φ来表示,这代表了斜桥斜的程度。记在斜支撑下横截面某点的应力值为σ1,在正交条件下(即φ=0°),横截面某点的应力值为σ2,定义β为应力变化率,则三者的关系如式(1)所示:

1.2模型的建立
利用有机玻璃实际试验尺寸来建立模型,有机玻璃为三跨连续梁,单箱双室的截面,两边跨均为1000mm,中间跨长为1200mm,设置4个墩,支座均设置在箱梁边腹板的下方,4个墩上的支座均为斜支撑支座,斜交角为30°,在这的斜交角定义为墩顶两支座连线与梁轴线法线所夹的锐角,共设置4个横隔板,每个横隔板均在支座连线处。弹性模量为E=3.3GPa,泊松比为μ=0.375。箱梁的尺寸如图1所示。
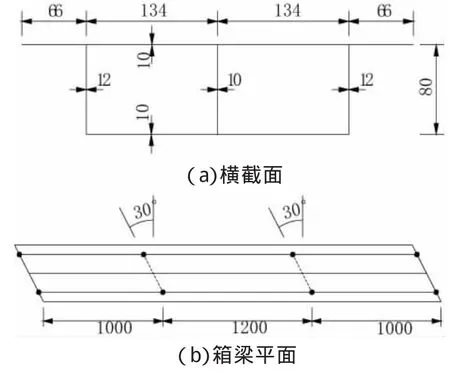
图1 箱梁简图(单位:mm)
箱梁所受的集中力在跨中截面腹板上方,集中力大小为P=980N,方向竖直向下,如图2所示。本文研究的截面是跨中截面,距离梁的两端均为1600mm,在跨中截面取主要的12个点的应力作为研究对象,如图3所示。所有12个应力点都是在斜交角为15°、30°、45°、60°和0°下取得的,其余建模的参数及步骤都是相同的,保证了只有角度一个量的变化对跨中截面应力的影响。
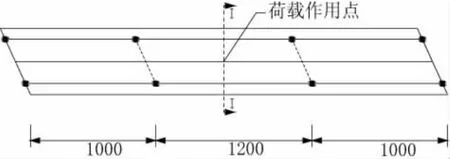
图2 计算截面及荷载作用位置(单位:mm)
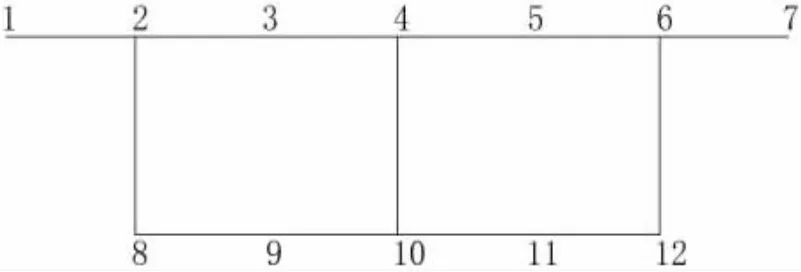
图3 对应截面计算的编号
在建立有限元模型时,采用ANSYS中SHELL63壳单元分析,每1mm划分一个单元,采用自由映射网格划分,图4为有限元简图。

图4 有限元模型简图
2 斜交角对应力的影响
2.1斜交角对顶板应力的影响
在应力分析时,集中力作用点处的应力不能作为有效的计算点分析,因为集中力作用点处会产生应力集中现象,应力值特别大,故不做分析,在此只作为参考值。
斜交角为60°时,顶板上7个计算点的应力值均有大幅度的减小,应力减小率最大,达到53%之大,最小减小率为46%,斜交为60°时,顶板有效计算点的应力减小率在46%~53%之间。斜交角为45°时,最大应力减小率为48%,最小应力减小率为16%,应力减小率在16%~48%之间;斜交角为30°时,最大应力减小率为39%,最小应力减小率为5%,应力减小率在5%~39%之间;斜交角为15°时,最大应力减小率为33%,最小应力减小率为4%,应力减小率在4%~33%之间。
分别将0°、15°、30°、45°、60°顶板上计算应力的值描点法画在二维坐标系中,如图5所示。
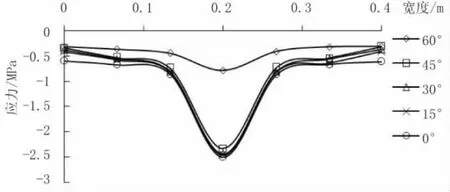
图5 顶板计算点的应力坐标图
2.2斜交角对底板应力的影响
底板共设有5个计算点,每个计算点均无应力集中现象出现,故5个点都可作为有效计算点,如图6所示。
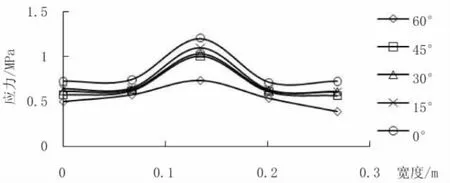
图6 底板计算点的应力坐标图
斜交为60°时,最大应力减小率为56%,最小应力减小率为23%,底板有效计算点的应力减小率在23%~56%之间。斜交角为45°时,最大应力减小率为21%,最小应力减小率为15%,应力减小率在15%~ 21%之间;斜交角为30°时,最大应力减小率为15%,最小应力减小率为11%,应力减小率在11%~15%之间;斜交角为15°时,最大应力减小率为12%,最小应力减小率为9%,应力减小率在9%~12%之间。
3 斜交角系数的确定
通过以上数据的分析,很明显可以看出在斜支撑条件下,对应跨中截面的计算点的应力值都要小于正交支撑的。而且应力的减小率随着斜交角的变化而变化。
斜交角的存在导致计算截面上各个计算点的应力值与正交的不等,利用斜交状态下对应计算点的应力值和正交状态下对应计算点的应力作比,这个比值就是所要求的应力变化率。跨中对应计算点的应力变化率见表1。
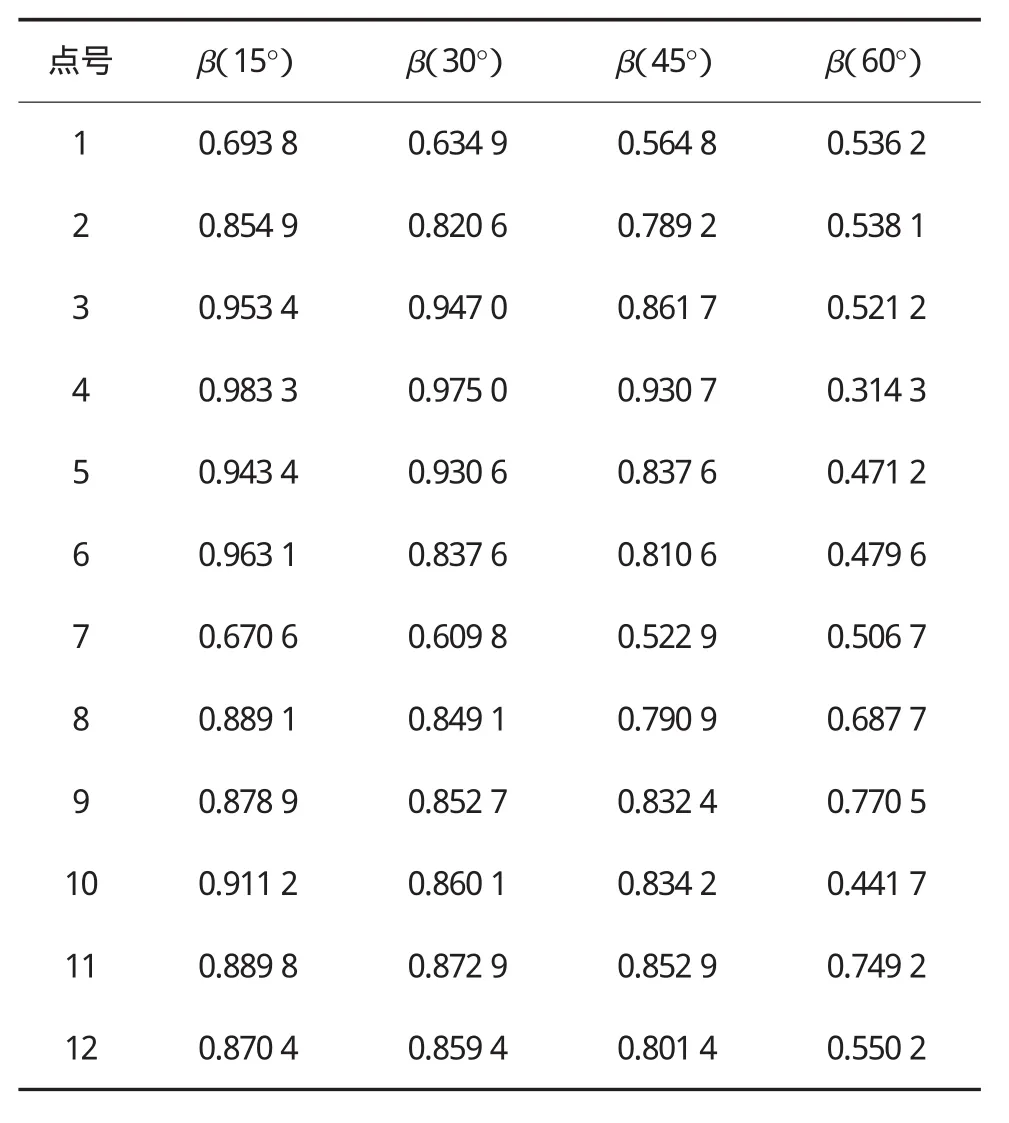
表1 应力变化率值
由表1可以看出,各个计算点的应力变化率均小于1,在斜交度为60°时,应力变化率最小,随着度数的减小,应力变化率在增大。应力变化率为60°时,应力变化率出现在5号点,翼缘板上的计算点的应力也较小;应力变化率为45°时,应力变化率最小值出现在两边的翼缘板的两个计算点上,即1点和7点,而越靠近集中力作用位置,应力变化率却在增大;应力变化率为30°时,应力变化率的最小值也出现在翼缘板的1点和7点,其他点越是靠近集中力,则应力变化率越大;斜交角为15°时,应力变化率最小值同样出现在翼缘板的1点和7点上,而靠近集中力的计算点应力变化率很大。
4 结 论
本文利用ANSYS分析软件中的SHELL63单元对斜支撑三跨连续双室箱梁建立有限元模型,分析了在集中荷载作用下不同的斜交角对跨中截面应力变化率变化的影响。
通过本文的研究工作可得出下列主要结论:
(1)在集中荷载作用下,不同斜交角下的应力变化率随着角度的增大而减小,同样的条件下顶板的减小幅度大于底板的。
(2)不同的斜交角下,最小的应力变化率均位于翼缘板上,故斜支撑下斜角度对翼缘板的影响最大。
(3)当斜交度小于45°时,应力变化率的变化较小;当斜角度大于45°时,应力变化率的变化很大。
[1]俆若昌,张元海.斜支撑箱梁桥的结构反应[J].土木工程学报, 1992,25(4):15-22.
[2]张元海.斜支撑连续梁内力计算及影响因素分析[J].兰州铁道学院学报,2000,19(6):41-44.
[3]苏燕东,李琳,白昕,等.斜交角对斜支撑连续箱梁应力影响的研究 [J].兰州交通大学学报,2013,32(3):8-11.
[4]曾丽.斜梁桥的组合有限元计算分析 [J].工程结构,2003,23 (4):44-46.
[5]林玉良,李威.斜梁桥力学特性分析[J].北方交通,2006,9(4): 54-57.
[6]李国豪.斜交结构的斜梁桥的荷载横向分布分析[J].同济大学学报,1994,22(4):395-400.
[7]刘菊玖.对斜梁桥荷载横向分布部分特点的探究 [J].市政技术,2002,3(3):42-45.
[8]黄平明.斜梁桥模型试验研究 [J].西安公路交通大学学报, 1999,1(1):41-44.
[9]黄平明.混凝土斜梁桥[M].北京:人民交通出版社,1999.
[10]姚玲森.曲线梁[M].北京:人民交通出版社,1989.
U441
A
1009-7716(2016)11-0127-03
10.16799/j.cnki.csdqyfh.2016.11.036
2016-07-20
刘亮(1991-),男,甘肃天水人,硕士,助理工程师,从事桥梁设计工作。
