知其然、知其所以然、知何由以知其所以然——由2016年浙江理第19题引发的数学解题教学的思考

☉山东省青岛第二中学 牟庆生

知其然、知其所以然、知何由以知其所以然
——由2016年浙江理第19题引发的数学解题教学的思考

☉山东省青岛第二中学 牟庆生

数学教育家傅种孙先生曾言：“几何之务不在知其然，而在知其所以然；不在知其然，而在知何由以知其所以然.”这为数学解题教学标明了三个递进的境界：一是知其然，二是知其所以然；三是知何由以知其所以然.数学解题教学，不能满足于一，应该立足于二而求三.下面笔者就结合2016年浙江省高考数学理科第19题的教学过程，谈谈对此的看法.

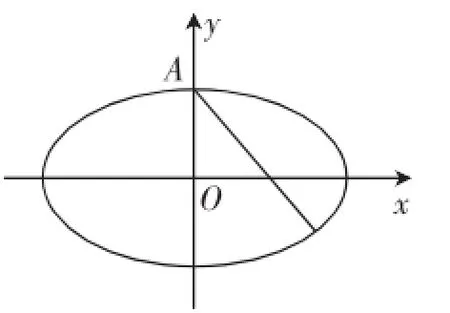
图1

（Ⅰ）求直线y=kx+1被椭圆截得的线段长（用a、k表示）；

（Ⅱ）若任意以点A（0，1）为圆心的圆与椭圆至多有3个公共点，求椭圆离心率的取值范围.

分析：第（Ⅰ）问属于常规问题，设截得的线段为AP，容易求得|AP|=此题研究的重点是第（Ⅱ）问.

一、知其然

1.阅读审题知“求什么”

解答任何一个数学题目之前，都要先进行读题与审题.通过审题明确考查的知识要点，分析题目的已知条件和待求结论，理解题意并且初步确定解题方向.

上述题目的第（Ⅱ）问考查的是圆与椭圆的位置关系，已知条件：“定点A”，“圆与椭圆至多有3个交点”；结论：“求离心率的取值范围”.显然，条件与结论之间的联系并没有像第（Ⅰ）问那么显而易见，这就导致学生认知上的困难.

2.操作演示知“是什么”

当题目呈现的内容比较复杂，学生难以从字面上获得解题的直接线索时，就需要借助“操作演示”来促进学生对问题的理解.“作图”是找到问题切入口的最有效的方法，可以让学生手工作图，也可以让教师通过几何画

板进行演示，从而获得最直观的解题经验.

过A点作半径大小不一的圆，发现圆与椭圆交点的个数有0、1、2、3、4等五种情况，而且交点的个数除了与圆的半径大小有关，还与椭圆的圆扁程度相关，而离心率的大小决定了椭圆的圆扁程度，这就明确了条件与结论之间的联系.

3.类比化归知“如何求”

理解题目的过程实际上就是“自然语言”转化为“数学语言”的过程，当题意理解透彻后，解题就进入了“数学建模”阶段，而数学建模的关键是对数学思想的灵活运用.通过类比、化归等数学思想，把不熟悉的数学问题转化为熟悉的问题.

图2

类比问题（Ⅰ），发现直线y=kx+1恰好经过定点A，AP就是圆与椭圆的一条相交弦.连接点A与交点，就得到一条相交弦；有几个交点便有几条等长的相交弦，交点问题就转化为弦长问题.至此，本题的解题思路就清晰起来了，如图2所示.

解析：先考虑与椭圆有4个交点的情景，然后排除这种情景，就可以得到符合条件的结论.

假设圆与椭圆的公共点有4个，由对称性可设椭圆左侧上有两个不同的交点P，Q，满足|AP|=|AQ|.记直线AP，AQ的斜率分别为k1，k2，且k1，k2＞0，k1≠k2.

二、知其所以然

1.反思回顾知“隐藏的真相”

解题教学并不是以获得正确答案为最终目的，而是通过经历一道题的解决过程，发现解题规律，揭示本质，从而获得一类题的解题思想与方法.要实现这一目的，解题后的反思回顾是必不可少的环节.弗赖登塔尔就曾精辟指出“没有反思学生的理解就不可能从一个水平升华到更高的水平”，通过反思回顾可以发现隐藏在问题表象下的“真相”.

综上可知，交点个数等价与相交弦的条数，最终转化为相交弦的长度问题，而相交弦AP的长度是在变化的，易知其在椭圆上的某个位置取到最大值.当动圆半径小于或等于AP的最大值时，就有可能出现1、2、3、4个交点的情况.当然，这要取决于AP取到最大值时所在的椭圆上的位置.若AP在椭圆的左右两侧取到最大值，则当动圆的半径小于AP时，就有可能出现椭圆左右两边各2个交点，一共出现4个交点的情景；为了避免这种情况的发生，只有当AP取到最大值的位置在椭圆短轴的下端点时才不会出现4个交点的情景，此时，无论动圆的半径如何变化，出现交点的个数只能是0、1、2三种情况.至此，我们就知道了交点个数取决于弦长最值所在位置这一“隐藏的真相”.

2.转变视角知“思维的变通”

在解题教学中，对同一数学问题的多角度审视可以引发不同的联想，发现不同的解题路径.这样既有利于问题的解决，又能使思维起点和过程都具有高度的灵活性，从而摆脱传统的窠臼，发现解题的捷径.

首先，若把题目中的椭圆看成圆，众所周知，圆与圆最多有两个交点.由此我们得到启示：椭圆越接近于圆，越不会出现超过3个交点的情况，因此，椭圆的离心率越小越好，于是可以推测题目的答案一定是“e∈（0，m］，其中0＜m＜1”.

其次，若从弦长最值出发，这道题的解答过程就会简洁的多.

要使|MA|2在y=-1处取到最大值，则二次函数的对称轴y=，解得1＜a≤，所以

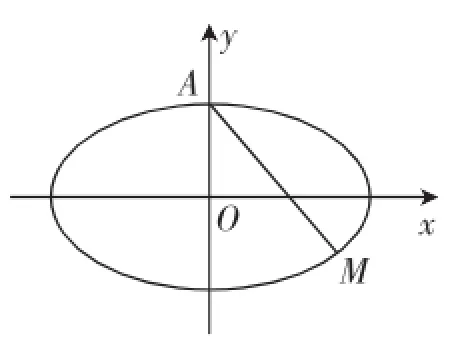
图3

解析：如图3，设M（x，y）是椭圆上一点，连接MA，则|MA|2=x2+（y-1）2=a2（1-y2）+（y-1）2=（1-a2）y2-2y+a2+1，y∈［-1，1］.

三、知何由以知其所以然

1.追根溯源知“曾经相识”

著名数学家华罗庚先生说：“数学是一个原则，无数内容，一种方法，到处可用.”尤其是经历高考复习后，通过解题教学与大量的训练，学生已经掌握了多数题型的解题方法与策略，但为何在正式考试中，还会碰到大量无从下手的题目呢？不排除有个别题目确实比较“新颖”外，主要原因是题目“伪装的太好”，很多看似陌生的题目其实都是学生的“旧相识”.只是学生无法快速识破这些“伪装”，从而无法与已有的解题经验建立有效的联系.这就需要教师对这些问题追根溯源，除去披在题目上的“马甲”，还原问题的本质.

作为今年高考的压轴题，此题的命题风格与往年大为不同.往年圆锥曲线解答题的条件与结论之间的联系明确，考查的重点在于运算与化简；而今年却截然相反，考查的重点转移到对题目的理解及转化上.如此违背“常规”的考查，令学生措手不及.其实，同类问题在平时练习中屡见不鲜，遗憾的是学生没有意识到它们之间的联系.

原题：若以原点为圆心，椭圆的半焦距长c为半径的圆与该椭圆有四个交点，则该椭圆的离心率的取值范围为____________.

分析：圆与椭圆的交点个数取决于圆的直径与过椭圆中心的弦长之间的大小关系.可知过椭圆中心弦的长度在［2b，2a］之间变化，要出现四个交点，则满足2b＜2c＜ 2a，可得.此题与高考题的类型及解题思路基本一致，唯一的区别就是圆心的位置从原点移到了短轴的顶点，从而导致椭圆弦长的变化规律不像原先那么直观，这就需要用到以下结论：

②当b＞c时，直线被椭圆截得的最大弦长为d=2b，即为短轴长.

这个结论是椭圆中比较常见的一个几何性质，很容易证明.

设M（x，y）是椭圆上一动点，则d2=x2+（y-b）2=a2·

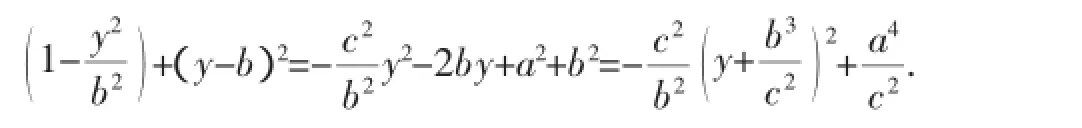
综上可知，此高考题是上述“原题”的变式，考查的是对上述椭圆弦长性质的“逆”应用，即通过弦长最大值的取值回溯条件“b＞c”，而这个条件恰好反映了椭圆离心率的大小.

2.变式拓展知“本质属性”

变式的意义在于通过对原命题的合理转化，达到学生对于数学对象本质属性的掌握.变式训练既预示着原有解题任务的结束，又开启了新的解题任务，在解题教学中起到了承上启下的作用.同时变式训练对于提升学生抽象概括能力、数学理解能力、解题能力具有不可替代的作用.

由上述高考题，可以作以下变式.

变式2：设F1，F2是椭圆=1（a＞b＞0）的左右焦点，若椭圆上一点P满足|PF2|=|F1F2|，且以原点O为圆心，以b为半径的圆与直线PF1有公共点，则椭圆离心率的取值范围为______

通过变式进一步掌握不同位置下椭圆弦长的变化规律，掌握求离心率问题的一般方法.

数学解题教学的重点不在于能解决多少数量的题目，也不在于获得正确的答案，而是要立足于“知其然、其所以然、知何由以知其所以然”这三个思维层次，对问题进行全方位的剖析，揭示其本质，从而获得最直接的解题经验与思想方法，建构与完善学生数学思维体系.F