以函数对称性为视角的命题探究——从函数的奇偶性说起

☉河南省商水县第二高中 黄俊峰

以函数对称性为视角的命题探究
——从函数的奇偶性说起

☉河南省商水县第二高中 黄俊峰

对称性是函数的重要性质，也是高考的重要考查内容，从内容上来看函数的对称性主要包括：轴对称与中心对称.

例如，奇函数和偶函数就是两类特殊的对称函数，其定义域为关于原点对称的对称区间，其中奇函数关于原点对称，偶函数关于y轴对称.即奇函数在其定义域内满足f（-x）=-f（x），偶函数在其定义域内满足f（-x）=f（x）.

利用奇偶函数对称性的相关结论常可简洁解题，如偶函数在对称区间内的最值相同、单调性相异；奇函数在对称区间内的最大值与最小值互为相反数，对称区间内的单调性相同等.

例1已知（fx）在其定义域R内满足（f-x）-（fx）=0，且在区间（-∞，0）上单调递增.若实数a满足f（2|a-1|）＞（f-），则a的取值范围是______.

解析：由条件f（x）在其定义域R内满足f（-x）-f（x）=0知f（x）在定义域内为偶函数，且在区间（0，+∞）上单调递减，则不等式可转化为，即，所以|a-1|＜，解得

评注：本题的解答关键是由条件关系式f（-x）-f（x）= 0确定函数为偶函数，则函数f（x）关于y轴对称，再利用偶函数在对称区间内单调性相异及f（-x）=f（x）=f（|x|）列出不等关系进行求解.

令，则F（X）是R上的奇函数.

因为奇函数的图像关于原点对称，所以F（X）min+ F（X）max=0.

因为F（X）max=f（x）max-1=M-1，F（X）min=f（x）min-1=m-1，所以（M-1）+（m-1）=0，所以M+m=2.

除奇偶性这种特殊的对称关系外，还有如下几种对称类型，下面举例说明.

一、轴对称

（1）若f（a-x）=f（a+x），则函数f（x）的图像关于直线x= a对称；

（2）若f（a-x）=f（b+x），则函数f（x）的图像关于直线x=对称.

例3（2015年福建）若函数f（x）=2|x-a|（a∈R）满足f（1+x）=f（1-x），且f（x）在［M，+∞）上单调递增，则实数m的最小值等于_______.

解析：由f（1+x）=f（1-x）得函数f（x）关于x=1对称.

因为函数f（x）=2|x-a|的图像是由函数y=2|x|的图像向右平移a个单位所得，而函数y=2|x|的对称轴为y轴，故f（x）= 2|x-a|的对称轴为x=a，所以a=1，则f（x）=2|x-1|.

由复合函数单调性得f（x）在［1，+∞）上递增，故m≥ 1.所以实数m的最小值等于1.

评注：由条件关系式可判断函数的对称轴，进而确定出a的值是问题顺利求解的关键.

例4定义在R上的函数f（x）是偶函数，且f（x）=f（2-x）.若f（x）在区间［1，2］上是减函数，则f（x）（）.

A.在区间［-2，-1］上是增函数，在区间［3，4］上是增函数

B.在区间［-2，-1］上是增函数，在区间［3，4］上是减函数

C.在区间［-2，-1］上是减函数，在区间［3，4］上是增函数

D.在区间［-2，-1］上是减函数，在区间［3，4］上是减函数

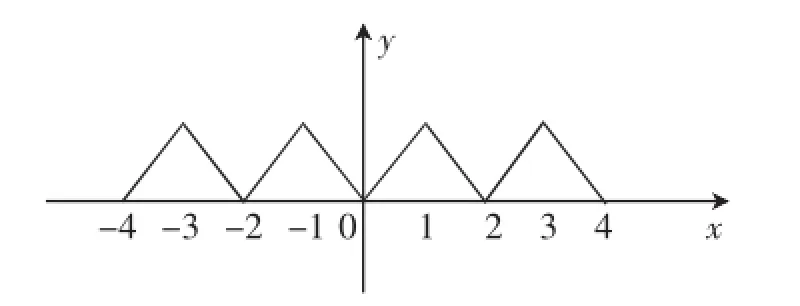
图1

解析：由f（x）=f（2-x）可知函数f（x）的图像关于直线x=1对称.又因为f（x）为偶函数，所以f（x）=f（x-2），所以函数f（x）为周期函数且周期为2，结合函数f（x）的图像（如图1）及在区间［1，2］上是减函数，知正确选项为B.

评注：注意对称性与周期性的区别，若关系式两边括号内的x的符号相同，则可得出函数的周期性；若两边括号内的x的符号相反，则可得出函数的对称性.本题求解中将偶函数与对称性相结合得出函数的周期性.

例5已知定义在R上的奇函数f（x），满足f（x-4）= -f（x），且在区间［0，2］上是增函数，若方程f（x）=m（m＞0），在区间［-8，8］上有四个不同的根x1，x2，x3，x4，则x1+ x2+x3+x4=（）.

A.-12B.-8C.-4D.4

解析：因为函数f（x）是定义在R上的奇函数，满足f（x-4）=-f（x），所以f（x-4）=f（-x），所以f（x）的图像关于直线x=-2对称，且f（0）=0.由f（x-4）=-f（x）知f（x-8）=f（x），所以函数f（x）是以8为周期的周期函数.

又因为函数f（x）在区间［0，2］上是增函数，所以f（x）在区间［-2，0］上也是增函数.

如图2所示，则方程f（x）=m（m＞0）在区间［-8，8］上有四个不同的根x1，x2，x3，x4，不妨设x1＜x2＜x3＜x4，由对称性

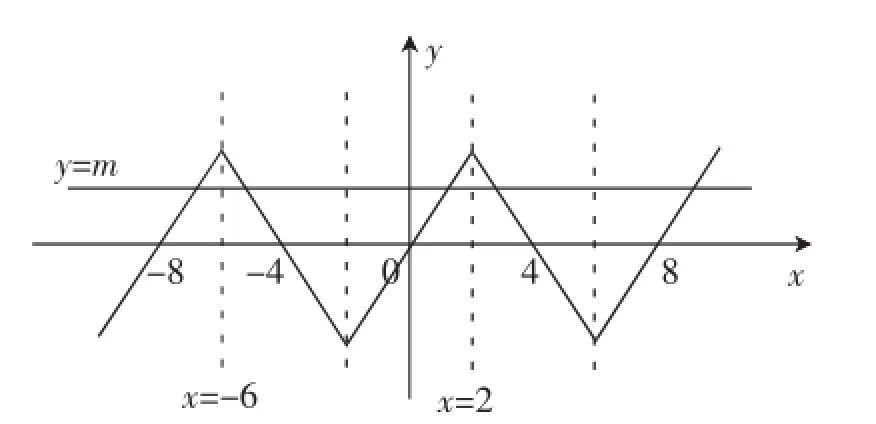
图2

同理x3+x4=4，所以x1+x2+x3+x4=-12+4=-8.

评注：本题求解中利用奇函数的性质，将对称性与周期性统一起来，得出函数的周期与对称轴.

二、中心对称

（1）若f（a-x）=-f（a+x），则f（x）的图像关于点（a，0）对称；

（2）若f（a-x）=-f（b+x），则f（x）的图像关于点对称；

（3）若（fa-x）=2b-（fa+x），则（fx）的图像关于点（a，b）对称.

例6（2016年全国卷Ⅱ）已知函数（fx）（x∈R）满足（f-x）=2-（fx），若函数y=与y=（fx）图像的交点为（x，

1

A.0B.mC.2mD.4m

解析：由f（x）=2-f（x）得f（x）关于（0，1）对称，而y=也关于（0，1）对称，所以对于每一组对称点

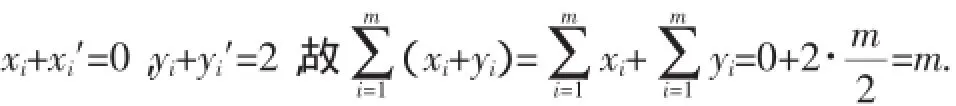
例7已知真命题“函数y=f（x）的图像关于点P（a、b）成中心对称图形”的充要条件为“函数y=f（x+a）-b是奇函数”.

（1）将函数g（x）=x3-3x2的图像向左平移1个单位，再向上平移2个单位，求此时图像对应的函数解析式，并利用题设中的真命题求函数g（x）图像对称中心的坐标；

解析：（1）平移后图像对应的函数解析式为y=（x+1）3-3（x+1）2+2，整理得y=x3-3x.

由于函数y=x3-3x是奇函数，由题设真命题知，函数g（x）图像对称中心的坐标是（1，-2）.

（2）设h（x）=log2的对称中心为P（a，b），由题设知函数h（x+a）-b是奇函数.

设f（x）=h（x+a）-b，则f（x）=log2，即f（x）=

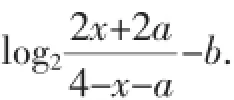
任取x∈（-2，2），由f（-x）+f（x）=0，得b=1.

所以函数h（x）=log2图像的对称中心的坐标是（2，1）.

评注：本题考查了函数图像及图像的变换、奇偶函数的对称性，熟练掌握函数图像平移变换法则及奇函数的定义和性质是解题的关键.

另外在处理有关函数对称问题时要注意区分函数自身的对称性与两个函数对称性的区别.两个函数间的对称性主要包括：两个函数关于x轴对称；两个函数关于y轴对称；两个函数关于原点对称；两个函数关于直线x= a对称；两个函数关于点（a，b）对称；互为反函数的两个函数关于直线y=x对称等.F