纠错应该是基于“究错”的纠错——例谈促进学生理解的纠错设计

☉浙江省严州中学梅城校区罗瑞根

纠错应该是基于“究错”的纠错
——例谈促进学生理解的纠错设计

☉浙江省严州中学梅城校区罗瑞根

在中学数学教学中，解题是中学数学活动的一个组成部分和主要形式，是学习数学课程的一个“实践性”环节，是实现教学目的的重要手段.波利亚说过：“中学数学教学的首要任务就在于加强解题能力的训练，……掌握数学就是意味着善于解题.”这充分说明了解题的重要性.数学教学离不开解题，解题在建立和发展学生的数学认知结构、形成和提高数学思维能力等方面起着不可替代的作用.

在解题的实践中，学生常常因为概念、方法、认识、观念、能力、意识等因素的影响而导致错误的发生，因此，纠错也就成为解题教学中的一项重要活动.由于课时的限制及教师自身的认识，对于学生所犯错误，教师纠错常对错因一带而过，或以一个反例简单说明，舍不得花时间或是不愿意深究，而把重心放在正确解法的讲解上，“正解”成为主要的，“究错”则成为次要的，是一种“生拉硬拽”式的纠错.这种做法的后果——一些学生考过、错过、讲过、订正过的题目，下次遇到学生还会错.只有让学生知其错知其之所以错，探究错误的内在原因，把握问题的本质，才可能理解、接受、反思、领悟正确的解法，进而能够迁移，真正达到纠错的效果、目的.文1谈了“利用错误资源，提高教育价值”，本文着重谈一谈对于“究错”，教师应根据不同类型的错误做好促进学生理解纠错的设计，采用不同的“究错”方式、策略.

一、以错“究错”，探错因深化认知

这是在学习了基本不等式的知识、方法后，由学生在一节习题课上提出的一个问题.

生1：可是这道题的参考答案不是这个结果，而我的做法中使用基本不等式的两次等号能够同时成立，我想不通是我错了还是参考答案错了.

生1：老师讲过，3个变量尽可能减少为2个变量，我就这样做了.

生2：要这样我也能做，但结果可以不同，难道题目有问题？

师：大家觉得是题目有问题还是方法有问题？

生3：还是方法有问题，要按照上面的方法，这样的操作有无数多种，每一种都能够保证等号成立，但是结果也就有无数多种.究其原因，虽然两次使用基本不等式时的等号都能取到，但第一次使用基本不等式时的等号仅是保证该不等式中的等号成立，却并非使用基本不等式的“最佳搭配”方式，因此无法真正求出u的最大值.

师：很好.生3提到了“第一次使用基本不等式的等号仅是保证该不等式中的等号成立，却并非使用基本不等式的‘最佳搭配’方式”，那什么是“最佳搭配”方式？谁能说说？

师：非常好，你能按照你的想法解这道题吗？

生4：因为a2+1+b2=，当且仅当a2=时等号成立.

生1：和参考答案一样.

师：大家说好不好？

众学生：好！

生5：其实不用换元就可以直接做，x2+y2+z2=所以u=，当且仅当时等号成立.不换元更容易发现x，y，z之间的内在联系.

师：太好了，掌声鼓励一下.生4、生5发现了题目的内在联系，尤其生5的方法更是让我们发现变形是x，z围绕着y进行的，要将y2合理地分配给x2，z2，“凑”出了问题的本质；而生1的方法为了过分地追求等号成立条件，开始只考虑x，z之间的关系，“牺牲”了y，将只该一步完成的工作人为地分为两步，生1的这种解法只是保证u能够取到，而不能使其一定是u的最大值，是对使用基本不等式求最值“一正、二定、三相等”条件的片面认识所造成的.感谢生1给我们提供了这样一个好问题.

学生认知上的一些“误区”往往会导致解题错误的发生，而且相应的错误具有很大的迷惑性，这类问题的纠错如果采用“急刹车”——教师直接告知正确的解法，为什么学生的解法错了没有说清、说深、说透，就容易使学生“不服气”，还觉得自己做的有道理，没错，导致纠错大打折扣，甚至有“翻车”的危险——下次遇到仍然重复自己根深蒂固的想法.纠错讲求“究错”，对于学生的这一类感到困惑的解题错误，教师可以故意“模仿”学生的错误解法，将学生引入“歧途”，导致自相矛盾，能够引发学生强烈的好奇心，激发学生的求知欲，这时再通过师生之间的互动，探讨错因，寻求正解.以错“究错”，可以暴露、放大错误，让学生参与其中探究出错的原因，学生想通了、理解了、接受了，自然会转变想法，在消除学生的困惑的同时，也深化了学生的相关认知，更能够建构完善学生的认知建构，而且对这类问题印象深刻，效果自然好于生硬的说教、直接的矫正.

二、以对“究错”，辨错因强化认知

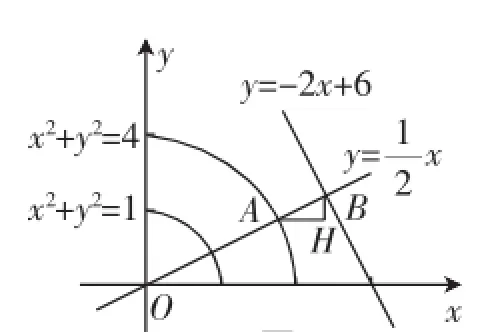
图1

例2已知θ∈R，实数x1，x2，x3，x4满足cosθ≤x1≤2cosθ，sinθ≤x2≤2sinθ，2x3+x4-6=0，求|x1-x3|+|x2-x4|的最小值.

这是一份练习卷上的题目，很多学生不会做，还有很多学生做错.主要的错误解法是：由条件可得1≤x21+x22≤4，且x1≥0，x2≥0，故点A（x1，x2）在圆环1≤x2+y2≤4位于第一象限所在区域内（包括边界），而点B（x3，x4）在直线2x+y-6=0上，如图1所示，原点O到直线2x+y-6=0的距离d=，所以ABmin=d-圆环大圆半径

2，此时直线AB与直线2x+y-6=0垂直，所以kAB=，所以

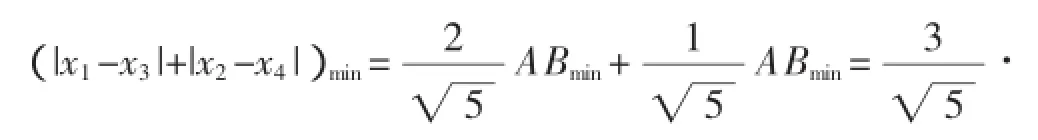
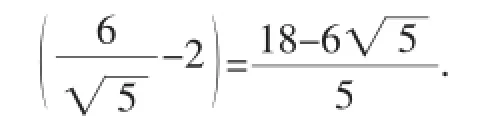
应该说，学生的解法很有代表性，符合学生解决直线上的点与圆上的点的距离问题的一般思路，也是有着很大的迷惑性.这种错误很难类似例1错解那样以错导

错，引发矛盾，因此，这类问题适宜在寻求正确解法的过程中探究错误的原因.教学过程如下：

老师首先展示了上述学生的解法.

师：在上述解法中，将问题转化为几何问题，大家觉得可行吗？

生1：应该可以，因为求最值问题的解决方法主要有两种：第一种，建立目标函数，转化为用函数研究、解决问题；第二种，利用问题的几何意义，从几何直观的角度求解.本题应该是用第二种方法.

师：生1说的非常好.但是这里面的|x1-x3|+|x2-x4|是否一定是上述解法中的AH+BH？

生1：我认为是的，从图像中可以看出来.

师：那这种方法应该没有问题喽？那么老师想问一下，本题中取到所求最小值时O，A，B三点是否一定共线？

生1：应该差不多.

师：那你的意思是能够从几何直观看出来？

生1：好像不能.

师：那就让我们试着用类似的方法在图像中表示|x1-x3|+|x2-x4|，注意只考虑A，B两点间的关系，O，A，B三点共线的情况我们已经看到了，暂时还不知对不对，因为这种看似由几何直观得出的结果必须保证其直观性的“依据”，而本题上述解法好像是缺少这种依据.我们看看能否找到“依据”？怎么去找？

生2：由图1变到图2，|x1-x3|+|x2-x4|还是等于AH+BH.

师：AB的走向只有这一种吗？

生2：还有两种特殊走向我给补一下，由图2变到图3.

师：那么在图3中，|x1-x3|+|x2-x4|如何表示？还是等于AH+BH吗？

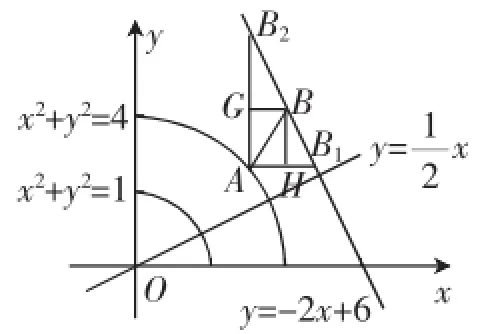
图3

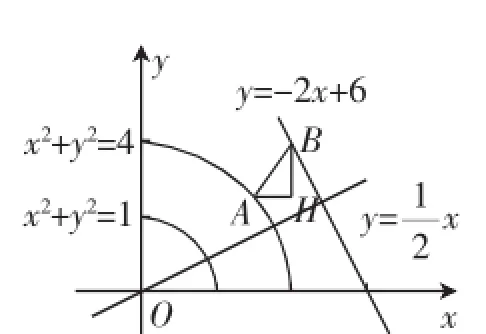
图2

生3：AB2垂直于x轴，|x1-x3|=0，|x1-x3|+|x2-x4|=|x2-x4|= AB2；AB1垂直于y轴，|x2-x4|=0，|x1-x3|+|x2-x4|=|x2-x4|=AB1.

师：就是说|x1-x3|+|x2-x4|的表示与AB的走向有关，有三种，哪一种最小？

生3：是的，每一种都要求一下才知道吧.

师：那么我们都试着求一下.

过了一会儿……

生4：AB2，AB1的最小值能够求出来，AH+BH的最小值好像不好求，求不出来.

师：那请你写一下AB2，AB1的最小值的求法.

生4板书：设A（x1，y1），B2（x1，y2），则f（x1）=AB2=y2-y1=-2x1+6-，求导得，令f′（x1）= 0，得x1=，再判断单调性可得（AB2）min=

生5：我还有更简单的方法.设A（2cosα，2sinα），则B2（2cosα，-4sinα+6），所以AB2=-4sinα+6-2cosα=6-同理可得，所以（AB2）min= 6-2.同理可得（AB1）min=3-

师：生4、生5分别用代数变量和角变量求出了AB2，AB1的最小值，三种情况解决了两种，离目标已经很接近了，好啊.但是只要有一种情况没解决，问题就没有结束，难点是AH+BH的最小值好像不好求，那么可不可以换一种思路，不好求能不能就不求也可以知道三种情况之间的大小关系.提示一下，还是从几何直观的角度.

生6：在图3中，由直线y=-2x+6的斜率为-2，可得AB2= AG+GB2=AG+2GB＞AG+GB=AH+HB=AH+2HB1＞AH+ HB1=AB1，这样在三种情况中，AB1最小.由生4、生5的方法就可以得到（AB1）min=3-，也就是|x1-x3|+|x2-x4|的最小值为3-

师：同学们觉得怎么样？

众学生：太棒了！

师：生1开了一个好头——从几何直观开始，定下了一个正确的方向；生2、生3准确地理解、直观地表示|x1-x3|+|x2-x4|是我们成功的关键；生4、生5解决了两种特殊情况的最小值的求解；生6完美“收官”，尤其通过“数形结合”合理地比较三种情况之间的大小关系，达到了“设而不求”的效果，解决了其中一种情况难以求解的困难，这种解题策略值得我们共同学习，而这正是开始老师所提到所要找的“依据”.同学们通力合作又为我们贡献了一场精彩的“思维盛宴”.这样，开始时的解法显然就是错误的，是对题意没有正确理解到位而导致的.

引导学生发现差异、联系与区别，能够类比已有的方法却又能够突破框框发现新的解题方法，消除思维定势的负向迁移，正确的理解、全面的考虑、准确的表达、合理的计算带来解题的成功，把握主次和轻重缓急.引导学生从正面探寻解决方法，这个过程也是不断探索、调整、纠偏的过程，正确的方法出来了，错误的原因也就发现了，可以强化学生正确的认知，更好地帮助学生生成知识、方法、思想、能力、意识，帮助学生在强化某类型问题形成方法的同时学会“转型”——防止思维定势，教师要有意识地注意思维定势对学生解题的负面影响，辩证看待，提倡既有思维的固定模式，更强调在理解的基

础上辨证灵活地看问题，优化学生的解题过程，提高学生的解题能力.

三、对比“究错”，明错因提升认知

例3已知函数y=log2（x2-2x+a）的值域是R，求实数a的取值范围.

这种题目在学过对数函数的知识以后会出现，老师讲过后学生再做的错误率仍然很高，于是老师再订正，但效果还是不好.对于这种问题的错误，可以通过以下的设计，通过对比探究错因，提升对问题的认识.

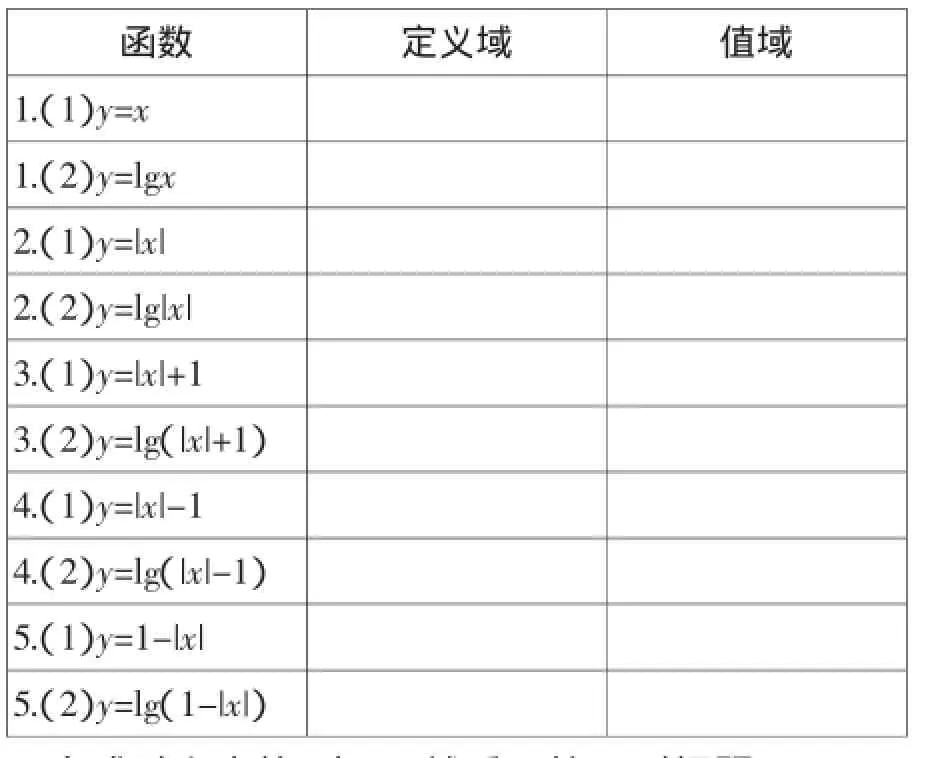
表1

完成以上表格（表1），然后回答下列问题.

问题1：通过对照比较，你能否观察得出同组两个小题中函数的定义域、值域的变化规律？

问题2：你能从以上例子中得出函数的定义域为R时函数要满足的条件吗？对于值域为R呢？

问题3：你能够画出以上函数的图像验证你的结论吗？

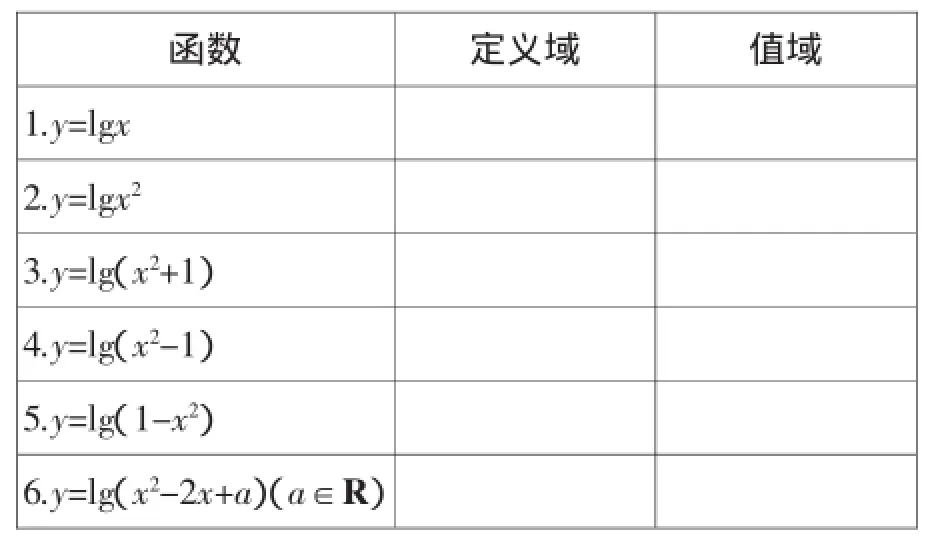
表2

问题4：你认为表2与表1的结果有何关系？

问题5：你能够画出表2中的函数图像吗？

问题6：你能够将表2中第2～6个函数转化为第1个函数吗？如果能够，如何转化？如果不能，请说明理由.

问题7：若函数y=lg（x2-2x+a）（a∈R）的定义域为R，则a的取值范围是_______.若函数y=lg（x2-2x+a）（a∈R）的值域为R，则a的取值范围是_______.

问题8：你能否再举出一些类似的例子？

华罗庚先生告诫我们：复杂的问题要善于“退”，足够地“退”，“退”到最原始而又不失去重要性的地方，是学好数学的一个诀窍.对于本题这样抽象性强，理解困难的问题，通过表1中的5组函数定义域、值域横向的变化对照，先“退”到简单的、特殊的、熟悉的函数模型，再从特殊到一般，提出3个问题，导向所要“究错”的问题上，然后再通过表2与表1中的函数定义域、值域的纵向对照，继续从特殊到一般，类比反思逐渐逼近目标.8个问题窜成一串，前后呼应，导向性明确，连同表格的设计在内始终突出“对照比较”，这也是提升这类问题认知的有效手段.问题3提示学生利用图像的直观性以提高对于问题形象性的理解，这儿的画图可以结合函数图像的对称性及函数图像的变换完成，画图的过程可以提高学生对问题的认识，而问题5中的表2中第3～6个函数的图像是很难准确并且直接地画出来（当然教师可以利用几何画板辅助作图帮助学生直观地观察理解），从而将学生的思维再导向简单的、特殊的、熟悉的函数模型，使学生能够运用换元法将问题转化为两个基本初等函数的复合函数的性质，在引导学生化归的同时，使学生能够真正认识、把握问题的本质.前6个问题是归纳的过程，而问题7、问题8则是从一般到特殊的演绎的过程，使学生在懂、会的基础上，能够运用、领悟.

教育家第斯多得曾说：“不好的教师是传授真理，好的教师是叫学生去发现真理”，教师的“教”是为了学生的“学”，教学中教师应充分发挥学生的自主性、积极性，从“教”变“导”.理解是学习者自觉克服旧的观念和习惯对他们的束缚而获得的，我们应该注意，即使那些成功的学生也可能不具备这种能力，教师能做的只是为学生创造条件促进理解的实现.教师应把研究的重点放在如何“带着学生走向知识”，而非“带着知识走向学生”.错解蕴含着丰富的资源，是学生学习和教师教学的宝贵资料，需要我们的智慧和精力去深入挖掘利用.错误是正确的先导，是成功的开始，我们应该积极主动去挖掘错误，剖析错解，防止类似错误的再发生.教师要针对学生不同的解题错误，做到具体问题具体分析，设计合理的教学环节，灵活地采用适当的“究错”方式、策略，引导学生学会探究、发现错误的原因，走向理解：可以反思总结错在何处，错因分析；应该怎么做，为何这样做；能否一题多解，哪种方法更优；能否变条件，变结论，多题一解；错解剖析，有何感悟等.让纠错时的“究错”成为一种习惯，成为一种能力，成为一种意识，能够深化、强化、提升认知，提高对数学的理解、领悟、把握，使解题正确、解题成功成为一种必然.F