跨越数学文化，打开数学学习的理解之路——以“平面直角坐标系”教学设计为例

☉江苏省无锡市侨谊实验中学茅莉萍

跨越数学文化，打开数学学习的理解之路
——以“平面直角坐标系”教学设计为例

☉江苏省无锡市侨谊实验中学茅莉萍

一、背景简介

目前，从中学数学的教学现状来看，现行的苏科版教材已经有了一些数学文化方面的素材来供学生学习，一些数学课外读物也专门设置了数学文化方面的相关内容来让学生进行学习，可见，数学文化走进数学课堂已经成为当下数学发展的一种趋势，正是在这样的背景下笔者以“平面直角坐标系”教学为例，设计了这样一节跨越数学文化，让学生更好地理解数学的专题实践课.

二、教学设计

（一）课前准备

1.复习数轴相关概念

（1）什么是数轴？____________________________

（2）如图1，指出数轴上A、B、C各点分别表示什么数：

图1

A点表示___，B点表示___，C点表示___.

（3）在图1所示的数轴上标出表示-1.5，0，3的对应点D、E、F.

（4）数轴上的点与实数之间是一种什么关系？_____________________________

2.预习“平面直角坐标系”

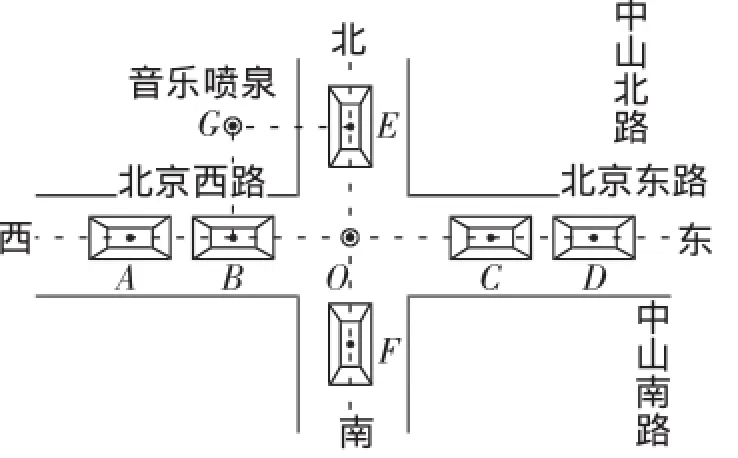
图2

图2 是某时刻拍摄的某地区的俯视图，此时汽车A、B、C、D、E、F离站台O的距离分别为200米、100米、100米、200米、150米、100米；音乐喷泉G距南北路100米，距东西路150米.

问题：（1）若把汽车、音乐喷泉、站台看成点，这两条路可以看成什么？

（2）你能用实数表示点A、B、O、C、D吗？谈谈你的想法.

（3）类比已解决的问题你能描述点E、F吗？

（4）结合生活中的实例，谈谈你准备怎么描述音乐喷泉的位置？

（二）课中探究

1.平面直角坐标系

平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系，简称为直角坐标系（也称为笛卡儿坐标系）.在这里穿插介绍笛卡尔建立平面直角坐标系相关的数学史的知识，让学生能够更好地理解平面直角坐标系建立的历史和文化.随之提出问题：（1）要建立平面直角坐标系，在平面上必须画几条数轴？（2）这两条数轴要满足哪些条件？（互相垂直、原点重合且具有相同单位长度）

2.象限

图3

坐标轴将平面分成的四个区域称为象限，按逆时针顺序分别记为第一象限、第二象限、第三象限、第四象限.如图3所示的坐标轴上的点（如点A、B、O、C、D、E、F）不属于任何象限.

3.点的坐标

（1）已知点的位置确定坐标.

问题：①结合生活中的实例，谈谈你准备怎么描述音乐喷泉的位置？

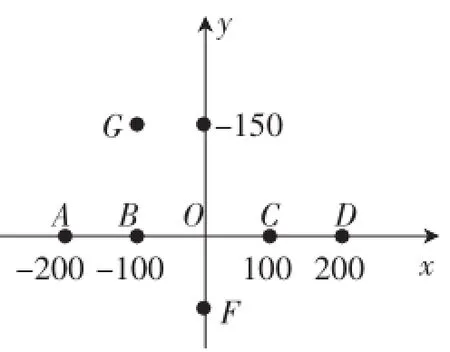
图4

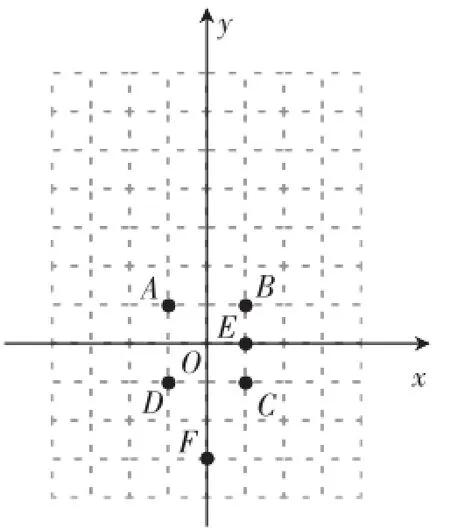
图5

②在直角坐标系中，能用两个数据描述点G的位置吗？如何描述？

辨析：能指出（150，-100）所表示点的位置吗？是点G吗？（利用图4研究）

酒款亮点：皮耶诺酒庄（Pierro）创立于1979年，庄主麦克·彼得金（Michael Peterkin）的热情和充满创意的酿酒技术，让皮耶诺的葡萄酒很快就打出知名度。如今，皮耶诺的红葡萄酒已经跻身产区顶级行列，出产的白葡萄酒更是声名显赫，尤其是皮耶诺的霞多丽，被称为世界级的精品白葡萄酒，为玛格利特河产区赢得了“真正的精品霞多丽之乡”的美誉。酿酒葡萄按照成熟度手工分批采摘，20%在新法国桶和1-2年法国桶中发酵熟成,80%在不锈钢桶中发酵熟成。LTC表示Little Touch of Chardonnay，是皮耶诺最受欢迎的特色酒款之一。

尝试：在平面直角坐标系（图5）中，写出点A、B、C、D、E、F的坐标.

（2）已知点的坐标确定位置.

尝试：在平面直角坐标系（图5）中，写出点A、B、C、D、E、F的坐标；描出坐标（-3，6）、（0，6）、（3，6）、（3，3）、（3，-3）、（-3，-3）、（-1，0）、（-3，3）所对应的点G、H、I、J、K、L、M、N.

（三）探究规律

探究1：平面直角坐标系中点的坐标的特征：各个象限内点的符号特征；各个象限内点的绝对值特征；坐标轴上点的坐标有何特征.

探究2：（1）一般情况下，表示点的坐标的两个数值不能互换，有没有一个点的坐标，它的两个数值可以互换？若有，它在哪里？（2）二四象限角平分线上的点的坐标有什么特征？（3）对于点P（a，b），a的数值变化、b的数值不变，那么点P的位置会发生怎样的变化？（4）对于点P（a，b），a的数值不变、b的数值变化，那么点P的位置会发生怎样的变化？

（四）小结提升（对本课进行完整总结，六个“一”）

一种方法——确定点及图形的位置；

一种思想——数形结合（数缺形时少直观，形缺数时难入微）；

一次经历——建立平面直角坐标系及其运用过程；

一份收获——多了一种解决问题的工具，解决问题的思想方法；

一种文化——数学本身就是一种文化的传承.

三、教学思考

1.重视与文化背景的联系

《义务教育数学课程标准（2011年版）》中关于数学文化的教学建议：选择介绍一些对数学发展起重大作用的历史事件和人物，介绍有关的数学背景知识.本节课正好结合笛卡尔建立平面直角坐标系的历史来进行关联，这样的设计和实施，就是将着眼点放到数学文化的层面来有效的进行，很好地拓宽了数学教学中关于数学文化的理解，从而也认识了数学文化中具有的丰富联系.当然，数学文化的渗透，我们可以从两个方面来实现跨越：其一，横向的跨越，横向的联系可以与其他学科的知识进行联系，其中如果能贯穿数学与思维领域的联系则效果更好；其二，纵向方面的联系，这里是指与学生学习数学过程中所处的文化背景的关联，以及每一位学生的数学实际情况，包括所接触的现实世界中的数学规律、概念及相关的数学知识结构.回到本节课中，笔者努力创设问题情境，并进行了尝试和实施，将生活中的实例引入，抽象出数学的模型，让学生身临其境，从而更好地理解平面直角坐标系的相关概念，也是对学生学习兴趣的一种有效的激发.

2.数学化理解——逐步抽象，过程递进

弗赖登塔尔认为，数学化就是数学地组织现实世界的过程，同时，数学化的对象也可以分为两类：一类是现实客观世界，另一类就是数学本身.如果由此理论出发，数学化的理解也可分为横向和纵向两种情形，通过以上两种情形，运用相关的数学概念、关系、问题、方法、思想的数学语言，传递信息、情感与观念的过程.回到本课中来，为了让学生自觉体会到数学是一种文化，通过教学过程的自然深入，教师应当关注学生数学化的过程体验，而逐步抽象，过程递进正是数学化理解的特征所在.在“建立平面直角坐标系”的阶段，学生更多地感受到的是生活中的实例，数学来源于生活，但又不局限于生活，它必然是高于生活的，于是，教师指导学生从生活情境不断抽象出数学模型，从而很好地体验了笛卡尔建立平面直角坐标系的过程，这是一种对经验的尊重.从“历史发生原理”选择合适的教学手段，从而设置更加符合学生认知水平和经验的自然的教学过程，当然这样的过程也仅仅是一种手段或者工具，面对不同的教学内容，仍需进行区分对待，灵活地进行运用.

四、设计合理性与人性化的统一

笔者认为，跨越数学文化的理解教学，应当从数学本质（数学的文化本质）出发，建立数学与数学史、社会文化、数学应用等的联系，将数学文化与学生的认识和经验相关联.在平面直角坐标系的设计中，笔者也试图

让学生对其文化本质进行领悟和关联，即通过平面直角坐标系这样一种工具，建立起数与形之间的有效联系，通过工具寻找解决问题的方法和实质.当然，在学生的学习过程中，教师也可以放手让他们多交流，通过师生和生生之间的互动和交流，让学生对平面直角坐标系产生更深入的认识和理解，最终体验到数学本质的最高境界——数学从本质上来说就是一种文化.

五、核心统领，拓展升华

目前，数学核心素养已经越来越受到重视，也越来越提到议事日程上来了.而在课堂上，核心素养往往体现在核心概念上面.核心概念是指概念体系中居于核心位置的具有生成力的那部分概念，对于平面直角坐标系而言，就是建立的依据和方法，以及内在的一些联系.这种联系不仅局限在数学系统之内，还能够延伸到数学系统之外——将数学与数学以外的文化联系起来（具有文化关联性），教师围绕核心打破固定的数学教材界限和传统的教学内容，形成新的概念和想法，并给予学生一种全新的认识——正如这节课中六个“一”的概念，从工具、方法、思想，到经历、收获，最终实现的是文化上面的一次飞跃.当然，数学文化在数学教学中进行有效渗透也并非一朝一夕之事，但作为未来的发展方向也一定是大势所趋.

1.张维忠，汪晓勤.文化传统与数学教育现代化［M］.北京：北京大学出版社，2006.

2.李文林.数学史概论［M］.北京：高等教育出版社，2002.

3.弗赖登塔尔，著.作为教育任务的数学［M］.陈昌平，唐瑞芬，译.上海：上海教育出版社，1995.F