蕴涵厚重，关注思维——2016年浙江温州市中考压轴题赏析

☉浙江温州市教育教学研究院黄新民

蕴涵厚重，关注思维——2016年浙江温州市中考压轴题赏析

☉浙江温州市教育教学研究院黄新民

动态几何题是历年中考的热点题型，备受一线数学教师的关注.笔者以自己命制的2016年温州市中考数学压轴题为例，结合试卷答题情况，以飨读者.

一、题目与解

如图1，在射线BA、BC、AD、CD围成的菱形ABCD中，∠ABC=60°，AB=6.O是射线BD上一点，⊙O与BA、 BC都相切，与BO的延长线交于点M.过M作EF⊥BD交线段BA（或AD）于点E，交线段BC（或CD）于点F.以EF为边作矩形EFGH，点G、H分别在围成菱形的另外两条射线上.

（1）求证：BO=2OM.

（3）当HE或HG与⊙O相切时，求出所有满足条件的BO的长.

解：（1）如图1，设⊙O切AB于点P，连接OP，则∠OPB= 90°，得∠ABD=∠ABC=30°.所以BO=2OP=2OM.

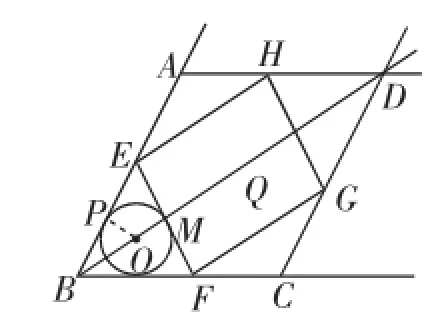
图1

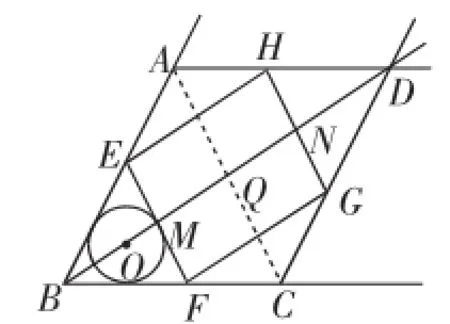
图2

（2）如图2，当点E在边AB上时，由条件得BD=18.

如图3，当点E在边AD上时，由对称性，得BM=3x=18-6=12，所以x=4.

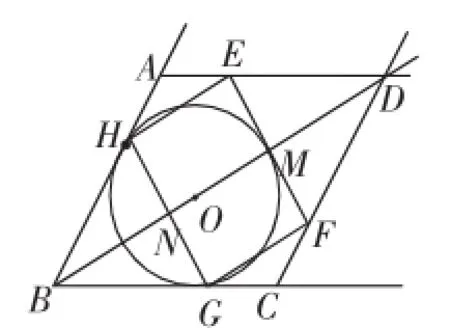
图3

综上所述，⊙O的半径是2或4.

（3）当点E在边BA上时，显然不存在HE或HG与⊙O相切.

图4

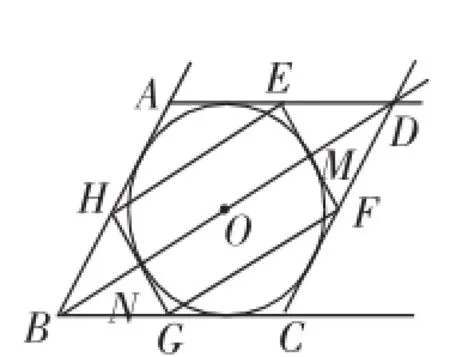
图5

①当点E在边AD上时，如图4，当HE与⊙O相切时，设EM=x，则DM=x.因为3x+x=18，所以x=9-3，即B0=18-6

如图5，当HG与⊙O相切时，由对称性，得ON=OM， BN=DM，所以BO=BD=9.

②当点E在边AD的延长线上时，如图6，当HG与⊙O相切时，设MN=2x，所以BN=x，所以DM=GN=BN=x，所以D与O重合.所以BO=BD=18.

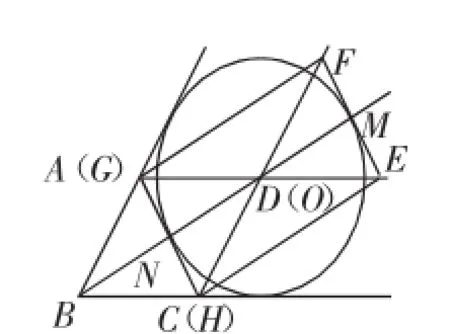
图6

图7

二、第（2）（3）问解法探究

1.第（2）问解法探究

当点E在边AB上时，下面给出几个不同于命题者的解答方法.

思路一：根据S矩形=EF·EH列方程.

另解1：如图8，由条件得BD=18，BM=3x，BE= 2x，得AE=6-2x.利用△AEH∽△ABD得=，则EH=18-6x.列方程得（18-6x）·2x= 24，再求解.

另解2：如图8，利用Rt△AEP的三角函数关系表示出EP=9-3x，则EH=18-6x，列方程得（18-6x）·2x= 24，再求解.

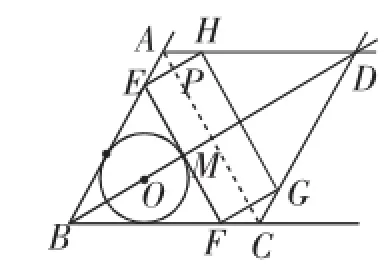
图8

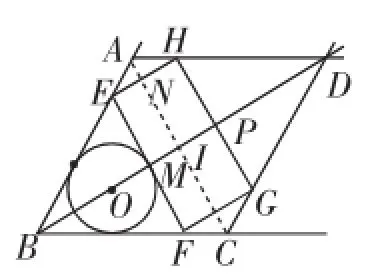
图9

思路二：根据S菱形=54列方程.

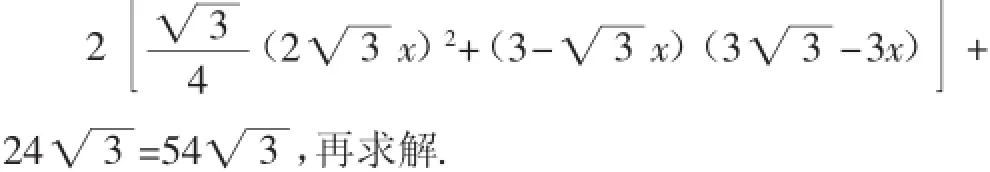
类似地，如图9，还可以根据S四边形EMPH=12、

S四边形EMIN=6等列方程.

思路四：根据BD=18列方程.

思路五：根据MI=EN列方程.

思路七：根据AI2+BI2=AB2列方程.

另外，根据不同的设元还可以得到不同的方程求解.

2.第（3）问解法探究

当点E在边AD的延长线上时，当HG与⊙O相切时，给出不同于命题者的解答思路.

思路一：根据PH=ME列方程.

另解1：如图10，由条件得DM=3r-18.在Rt△DME中，ME=.在Rt△BPH中，BP=r，则PH=.列方程得

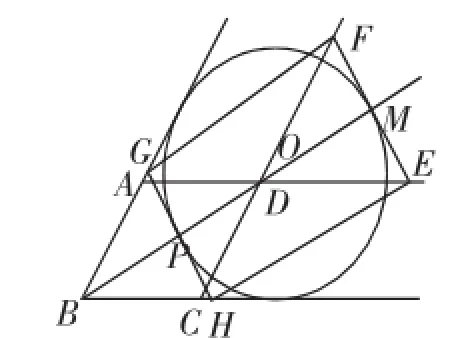
图10

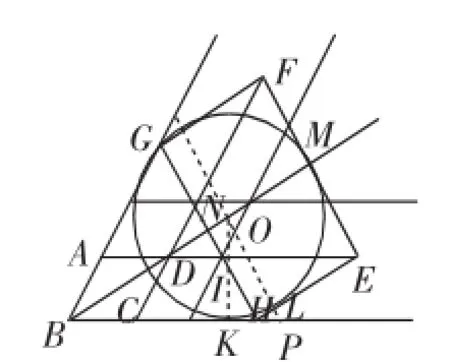
图11

思路二：根据BP=DM列方程.

另解2：可证明△BPH≌△DME，则DM=BP.由条件得DM=3r-18，列方程得3r-18=r，再求解.

当点E在边AD的延长线上时，当HE与⊙O相切时，下面给出不同于命题者的解答思路.

思路一：根据OK=OH+HK=r列方程.

另解1：如图11，由条件可得HE=18，所以HL=18-r，则NO=18-r，则IO=36-2r.因为HL=KH，可证△NIO≌△KIH，则IH=IO=36-2r，则IK=18-r，列方程得（36-2r）+（18-r）=r，再求解.

另解2：如图11，由条件得HL=18-r.在Rt△BOP中，

类似地，还可以根据HL=NO列方程求解.

另解3：如图11，由条件得HL=18-r.在Rt△HLP中，再求解.

三、亮点评析

本题构图优美，像一条纵身一跃的美人鱼.命题者在固定的菱形中，设置两个相互依赖的变化图形：圆和矩形，并以圆为主动带动矩形的变化.在整个变化过程中，随着点O的运动，圆逐渐变大，由于矩形的四个顶点可以落在菱形所在的射线上，从而使矩形的变化“神出鬼没”，反复经历三次从有到无的过程.第（1）问考查特殊角的三角函数关系，第（2）（3）问重点考查学生分析，解决动点问题的能力.在点O从B点出发，沿射线BD运动时，变化的量有半径的长度，HE、HG、GF与圆的位置关系，△AHE、△GCF、△HBG、△EFD和四边形HGFE的面积.命题者选取了变化中的特殊情况进行考核：当矩形EFGH的面积等于某一值时，或当HE（HG）与⊙O相切时，求⊙O的半径.数学研究在本质上是研究数量和图形，求变化中的数量的特殊情况是研究数量关系的关键，求变化中的图形的特殊状态是研究图形关系的关键.通过第（1）（2）问的铺垫，让学生意识到，运动过程中BO=2OM是不变的，只要确定了矩形的位置，根据对称性就可以确定图形内部的数量关系，这为后续探究埋下了伏笔.第（3）问求出所有相切的情况，需要较高的分析和想象能力.然而，看似变化诡异，但学生如果能抓住圆和直线相切的本质：点到切线的距离等于矩形一边长的一半，即可跳出“形”的迷惑，也为问题解决提供了清晰思路.本题考查学生的数学学习能力，符合《课程标准（2011年版）》提出的数学教学内容的本质要求，让学生在开放的、动态的数学问题情境中，逐步识图、画图、分析推理、判断验证，突出了数学思维的考核.

本题将观察、分析、计算、探究，将菱形、圆、矩形、三角函数、方程、轴对称变化等初中数学的核心思想融为一体，蕴含着分类讨论、转化、方程、对称变化等重要的思想方法.总体设置由易到难，逐步推进，梯度合理，入口易，深入难，既关注学生的思维方法，又凸显数学本质，是对学生探究能力、创新能力的一次检验.

四、对教学的启示

1.夯实基础，关注核心教学内容

中考试题首先着重考查“课标”中要求的核心内容，即使是拔高性试题所注重的也是对支撑初中数学知识体系的基础知识、基本技能、基本方法的考核，这从本题考查的知识点可看出.因此要加强基础知识的落实，日常教学要关注《课标》的核心内容，运用初中数学知识体系的整体观思想，加强知识之间的联系和再生性，把握其中的数学思想方法.

2.加强学生对知识理解的活动经验的积累

学生学习数学有一个普遍现象，知识容易遗忘，不能灵活应用知识.解决此问题的较好的途径是重视知识形成的过程，加强对知识理解的活动经验的积累.《课标》特别强调：“数学活动经验的积累是提高学生数学素养的重要标志.帮助学生积累数学活动经验是数学教学的重要目标，是学生不断经历、体验各种数学活动过程的结果.”积累数学活动经验的目的之一是建立数学的感悟、数学的直观.日常教学重视过程教学，不仅有利于促进学生对知识的理解，更能从中学会分析问题的策略、方法，体会抽象、建模、推理的基本数学思想，有利于形成策略性知识，并运用于问题的解决，这是新课标积极倡导和要求的.

3.关注日常教学中分析、解决问题能力的培养

对试卷答题情况的分析，暴露了学生分析、解决问题能力的薄弱点，主要表现在以下几个方面：读题能力弱，不会分析运动过程，遗漏分类，画不出满足条件的图形，列出方程后求解错误.而随着越来越多的新颖题、开放性试题的出现，中考更多的是考查学生分析、解决问题的能力.这中间包括学生的探究、猜想、验证、归纳、实际应用、逻辑推理、分析问题、数据处理等方面的能力.这就要求我们在平时的教学中，要立足于对学生能力的培养，要让学生在发展能力的过程中接受新的知识，在知识的传授过程中锻炼学生的能力.

4.研究学情，寻找得分点

中考复习中，除了注意学生的学力发展，还要关注一些应试技巧和得分点.在对试卷分析中，教师今后要加强对学生以下几个方面的训练：（1）加强几何逻辑推理的严密性；（2）规范学生书写的文字表达；（3）注意解题速度和合理分配解题时间.Z