从特殊到一般：类比全等学相似——以“图形的相似”教学为例

☉江苏省灌南县实验中学韩贤

从特殊到一般：类比全等学相似——以“图形的相似”教学为例

☉江苏省灌南县实验中学韩贤

我们知道，平面几何教学时，都是先学全等，然后在等腰三角形、平行四边形等知识教学之后“隔了很久”才学习相似，而这两个知识领域却有着十分紧密的联系，全等可以看成是相似的特例（相似比为1）.本文记录新近笔者开设的一节公开课，基于从特殊到一般的数学思想，引导学生类比全等学习相似起始课，课后及时进行了教后反思，一并梳理出来，提供分享.

一、“图形的相似”教学流程

1.复习旧知，引入新课问题1：什么叫全等形？它们在形状、大小上有何特征？问题2：两个全等的三角形的对应边和对应角有什么关系？

PPT出示图片（如图1）.

问题3：它们是全等形吗？（不是）它们又有什么特点呢？（形状相同）

板书：我们把形状相同的图形叫做相似图形.

图1

2.巩固概念，识别相似

预设提问：

（1）你能举出生活中一些相似图形的例子吗？

（2）我们知道从物体的轮廓中可以抽象出几何图形，你能举出相似的几何图形的例子吗？

（3）图2中的三组图形，是否相似？

（4）如果图形A和图形B相似，图形B和图形C相似，请问图形A和图形C相似吗？为什么？（表明：相似具有传递性）

跟进练习：图5中哪些图形和图3相似？为什么？哪些图形和图4相似？

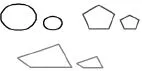
图2

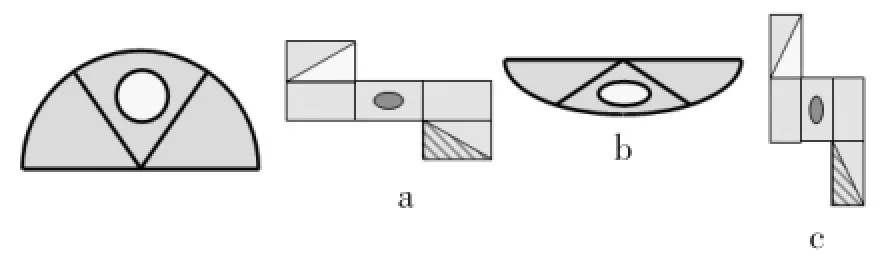
图3

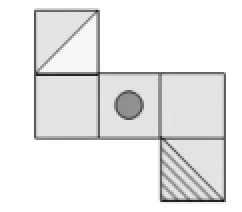
图4

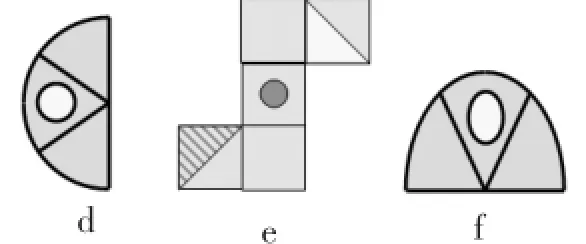
图5

追问：通过这个练习，你对图形的相似有哪些新的认识？（只与图形的形状有关，而与位置的摆放没有关系）

3.观察猜想与思考

提问：如图6，从放大镜里看到的三角尺和原来的三角尺相似吗？为什么？

追问：猜想一下，它们的对应角有什么关系？对应边又有怎样的关系呢？过渡：带着你的猜想、疑问进入下一阶段的探索吧！观察特例：

提问：请大家看图7，△A1B1C1就是由正△ABC放大后得到的，你认为它们的对应角有什么关系？对应边的比有什么关系呢？

图6

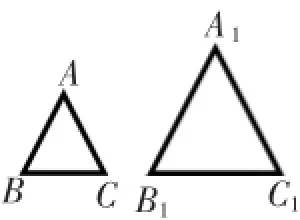
图7

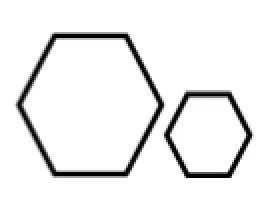
图8

追问：图8是两个相似的正六边形，你从中可得到什么结论？为什么？如果是两个正五边形呢？

通过刚才的研究，你能得出怎样的结论？（相似正多边形的对应角相等，对应边的比相等）

4.例题讲评

例1如图9，六边形ABCDEF与六边形A′B′C′D′E′F′相似.

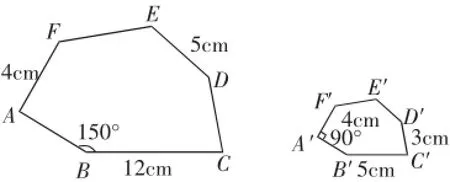
图9

（1）求相似比.

（2）求∠A和∠B′的度数.

（3）求边CD，EF，A′F′，D′E′的长.

（3）由两个六边形相似，引导学生灵活选取对应比成比例，比如由，所以所以，所以，所以CD=cm.

例2如图10，在一矩形花坛ABCD的四周修筑小路，使得相对两条小路的宽均相等.花坛AB=20m，AD= 30m.小马同学认为只要每条小路的宽都相等，所围成的矩形A′B′C′D′与矩形ABCD就一定相似.你认为小马同学的判断正确吗？

预设追问：试问小路的宽x与y的比值为多少时，能使小路四周所围成的矩形A′B′C′D′与矩形ABCD相似？请说明理由.

预设讲评：要使矩形A′B′C′D′与矩形ABCD相似，需对应角相等，对应边的比相等；由矩形的四个角都是直角，可知这两个矩形的对应角相等，所以，需对应边成比例，即，化简得60y=40x，即x∶y=3∶2时，能使小路四周所围成的矩形A′B′C′D′与矩形ABCD相似.

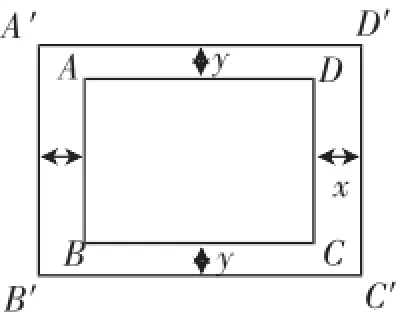
图10

5.小结与作业（略）

二、教学立意的进一步解读

图形的相似起始课因为没有具体深入到相似三角形的学习，而且在各级考试中所考不多，至多是一道填空、选择之类的送分题，所以往往得不到教学研究的重视，这方面的课例研究在相关期刊上也较为少见.以上给出的是笔者基于从特殊到一般的认识，构思出来的一节常态课，以下再围绕教学立意给出进一步的解读.

1.引导学生辨析“特殊与一般”之间的关系

特殊与一般之间的关系是数学学习过程中不断出现的，或明或暗.比如代数概念或性质的学习，往往是先特殊再一般，侧重训练猜想、归纳、概括的推理思想；而几何学习则是“从大到小”（史宁中教授语），先学习一般的数学对象（如四边形），再逐渐深入到平行四边形、特殊的平行四边形的学习.而在本课时中特殊与一般之间的关系较为复杂，首先是从全等到相似是特殊到一般的关系，然后是学习了相似图形之后又将逐渐过渡到相似三角形的判定与性质.

2.通过例题及变式让学生明辨“和而不同”

从上面课例中的例题及变式来看，主要意图是通过例题及变式促进学生感受全等与相似之间的“和而不同”，即全等有哪些相同的研究方法可以迁移、类比到相似的学习中去，而又有哪些不同点，特别是例2中两个矩形的相似问题是很多学生容易受到直觉误导的易错题，缺少精确的比例式化简运算，则不能有力地解释两个矩形为什么不相似，这就需要学生明辨相似图形不仅只看各组内角对应相等就可判定，还需要逐个计算各组边之间的比值，这是需要引导学生明辨的难点和易错点之处.

三、结束语

从应试角度功利地看，不少数学内容确实在各级考试中难以设计大题，因而也缺少研究的跟进，常常也在教学时被边缘化，认为这是一些可有可无的教学内容，有些年轻教师也觉得可讲可不讲，轻松滑过这些教学内容，但是从数学整体观来看，像图形的相似这样的教学内容却是学生辨析“特殊与一般”之间深刻关系的优秀素材，值得我们认真重视，精心预设相应的教学内容，这在倡导重视“数学核心素养”的现实背景下，也许有着更为重要的作用吧.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.鲍建生，顾泠沅，等.变式教学研究［J］.数学教学，2003（1，2，3）.H