“生活味”淡一点，“数学味”重一些——“平面直角坐标系起始课”的评课与商榷

2016-12-07江苏泰州市姜堰区实验初级中学邱晓敏

中学数学杂志 2016年18期

☉江苏泰州市姜堰区实验初级中学邱晓敏

☉江苏泰州市姜堰区实验初级中学邱晓敏

在最近一次地区青年教师赛课活动中，笔者观摩了多节平面直角坐标系起始课教学，不少教师大胆整合教材，在该课中不仅组织学习有序数对，而且引出平面直角坐标系的概念，并进行了运用与变式，体现了教师对数学概念在不同学段的精准认识，也有一些教学环节值得商榷.本文梳理出一种有代表性的教学流程与活动意图，并给出评课意见与商榷改进，供进一步研讨.

一、教学流程与活动意图

（一）趣味活动，引入新课

开课导语：老师今天准备了一本精美的图书，送给我们班级里的一位幸运星.

活动预设：学生抽签寻找这位幸运星.一名学生抽签，结果幸运星在第×列.这一位幸运星确定了吗？有几个？

学生继续抽签寻找这位幸运星，又一名学生抽签，结果幸运星在第×排.这样这一位幸运星能确定了吗？有几个？

约定：列数由左往右数，排数由前往后数.则上述位置可简记为（×，×）.

定义：像（10，12）、（5，4）这种用括号括起来的一对数我们把它叫作数对.

活动意图：师生之间较为陌生，通过师生交流拉近师生的距离.从具体情景中发现数学问题，进而寻求解决问题的方法，使学生认识到现实生活中蕴含着大量的数学信息.

（二）合作交流，探究学习

探究活动1：请结合“教室平面图”完成以下问题.（按照上面的约定）

（1）说出×、×同学的确切位置；

（2）我们来个比赛，看看哪组又快又准！

活动准备：课件展示问题：请找到如下数对表示的位置是哪个同学的座位.

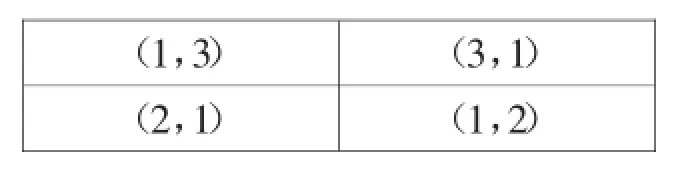
（1，3）（3，1）（2，1）（1，2）

预设追问：每一组的两个数对中的数字相同吗？指的是不是同一个位置？为什么？

引导学生得出结论：用同样的两个数表示位置，当两个数的顺序不同时，表示的位置也不同.

有序数对：把有顺序的两个数a和b组成的数对，叫作有序数对.记作：（a，b）.

活动意图：经历用有序数对寻找位置的过程并观察数对的特点，使学生感受有序的必要性，加深学生对有序的理解.

探究活动2：小明是光明中学刚入学的初一新生，他为了尽快熟悉校园，请高年级同学为他画了学校的平面示意图.如果用（5，2）表示图上校门的位置，那么食堂、教学楼、办公楼、宣传橱窗、实验楼、运动场的位置分别可以表示成什么？

8765432实验楼（3，7）运动场（6，8）食堂（9，6）11 2 3 4 5 6 7 8 9 10办公楼（3，3）宣传橱窗（2，2）教学楼（7，4）（5，2）校门

在生活中，还有用有序数对表示一个位置的例子吗？大家讨论一下.

……

活动意图：经历运用所学知识，寻找实际背景的过程，使学生体会到数学是解决实际问题和进行交流的重要工具，在现实生活中有着广泛的应用.

探究活动3：自然灾害对地球的影响日趋严重，同学们，你能在地图上告诉大家目前地震的震中的位置吗？

活动预设：要求学生在地图上确定一个地点的位置，需要借助经线和纬线，这两条线从局部上可以看成是平面内两条互相垂直的直线，是有刻度有方向的直线，进而抽象成数轴，而平面内，两条互相垂直且有公共原点的数轴，就如同地图上的经线和纬线，可以帮助我们确定平面内任何一个点的位置.

引出概念：平面直角坐标系.给出严格的平面直角坐标系的概念、画法及象限的规定.

活动意图：这一环节的教学，从学生感兴趣并与实际生活相联系的话题入手，能立刻激起学生的好奇心和求知欲，使他们思维活跃并有所期待.同时，将实际问题抽象成数学问题，使坐标系的产生这一难点的突破自然而然，水到渠成.

探究活动4：将任意点A放入直角坐标系，由其所处位置让学生确定点的坐标.在此过程中，学生将由点确定坐标的方法不断深化，逐渐接受并掌握点的坐标是一对有序的实数.同时，通过观察，学生容易发现，点在各个象限内及点在坐标轴上的坐标的特点.

预设追问：①点在各个象限的坐标有什么特点？②坐标轴上的点有什么特点？③坐标轴上的点属于第几象限呢？

活动意图：教师引导，学生观察、探索.学生在操作的过程中，能对平面直角坐标系的概念有更深刻的了解，同时也是对前面知识的整合和归纳.

（三）变式应用，巩固提高

探究活动5：（1）在网格的平面直角坐标系中随机描出有代表性的点A、B、C、D、E、F，要求学生读出它们的坐标.

（2）在平面直角坐标系xOy中，描出下列各点：A（4，3）、B（-2，3）、C（-4，-1）、D（2，-2）、E（0，-3）、F（0，0）

活动意图：让学生思考如何由坐标确定点的位置，由点的位置确定点的坐标，既是对学生能力的培养和促进，又能训练学生的数学结合思想，使学生成为课堂的主体，激发他们的学习热情.

探究活动6：互动游戏.以班里某个同学为坐标原点，建立全班范围的平面直角坐标系.

预设追问：①你所在的象限是？你的坐标呢？②x、y轴的同学你们的坐标有什么特点？③横坐标为2的同学起立，你们所在直线和y轴的同学是什么位置关系？纵坐标为-1的同学起立，你们所在直线和x轴的同学是什么位置关系？④你的坐标和你到x轴、y轴的距离有什么关系？

活动意图：在这个环节中，通过在全班展开互动游戏来深化本节课的教学，同时也是给学生提供合作交流、自主探索的数学活动机会.抽象又带有一定难度的结论由学生自己通过发现、感受、交流得出，让学生真正成为课堂的主人，使他们感受到获得知识的成功喜悦，激发其学习数学的激情.

探究活动7：展示本校所在地区的地图，找出学校的大致位置（图略）.

预设追问：生活中见到过坐标系有哪些作用呢？

活动意图：将知识及时联系生活实际，不仅能拓宽学生的视野，使学生感受到知识的应用价值，体验“坐标系”的科学和文化价值，同时也能使学生对本节课的认识由感性上升到理性.对本节课的教学起到画龙点睛的作用.

（四）回顾反思，布置作业（略）

二、评课意见与商榷改进

从上面的教学设计来看，教师整合教材，并没有只是围绕“有序数对”整节课“空转”，做低层次的小学复习任务，而是在经历几个探究活动之后就引出平面直角坐标系的概念，然后开展概念巩固与运用变式的训练.从整节课教学流程和环节预设上看，是一节不错的教学设计.然而从更具有数学味的初中数学课的高标准来看，还有一些值得商榷和改进的地方，分述如下.

1.增加“平面直角坐标系”概念的教学时间

从上面的教学流程、探究活动来看，平面直角坐标系这个新的概念，从它的定义、例题应用、巩固训练等角度来看，教学时间偏少，学生对这一新概念的理解需要必要的教学时间作保证，如果不能在第一课时学生新接触这个新概念时充分训练、促进理解的话，后面又将面临“夹生饭、反复炒”的尴尬境地.故我们建议这个新概念的教学时间要大幅增加，可以通过添加变式、同类问题多样化训练的方式来促进学生理解.

2.减少“有序数对”生活情境问题的教学时间

如上面所说，需要增加平面直角坐标系的教学时间，那么每个课时的教学时间是固定的，从哪儿挤出时间呢？可从这节课中出现的大量的生活情境问题、游戏等所谓的探究活动中挤出时间，这些“幼稚化”的生活情境问题在紧张的初中数学课堂教学中需要减少、再减少，把有限的教学时间花在更重要的新概念教学上.

3.重视渗透“数形结合”的数学思想方法

我们知道，平面直角坐标系是两条数轴垂直相交（原点为它们的垂足）所成，数轴的重要价值就是沟通数与形之间的关系，这里的数形结合思想方法在平面直角坐标系中是要引导学生重视的.可以通过设计不同角度的问题或变式追问促进学生加深理解.以下给出新接触平面直角坐标系这一工具时一组例题.

例1在数轴上的点A到原点的距离是1，则该点对应着数__________；从“数轴”到“平面直角坐标系”后，有一点B到原点的距离是2，则点B的坐标为_________.

预设解答：±1；（2，0）、（-2，0）、（0，2）、（0，-2）.

例2在平面直角坐标系xOy中，点A（2，3）、B（3，2）.

（1）说说点A、B的不同点与相同点（各写出两条即可）；

（2）连接OA、OB、AB，得到△OAB，试求它的面积.

预设解答：（1）不同点：①它们不是同一个点；②它们到x轴的距离不同；相同点：①它们都在第一象限；②它们到原点的距离相等；（2）2.5平方单位.

例3在平面直角坐标系中，点A在x轴上，位于原点右侧，距离原点2个单位长度；点B在x轴上方，y轴左侧，距离每条坐标轴都是3个单位长度.请利用所给的平面直角坐标系操作和求解.

（1）请标出点A、B，画出△OAB；