中美两国初中数学教材的比较研究——以“有理数”为例

☉西北师范大学教育学院徐玉庆

☉甘肃省酒泉第四中学

中美两国初中数学教材的比较研究——以“有理数”为例

☉西北师范大学教育学院徐玉庆

☉甘肃省酒泉第四中学

一、研究背景

《义务教育数学课程标准（2011年版）》明确提出，在数学课程中，要注重发展学生的数感和运算能力，这也充分体现了新课程标准对初中生核心素养的要求.［1［2］所以，运算能力是许多国家对中学生要求的最基本能力.

本文从美国和中国两个国家选取三套初中数学教材，以“数与代数”中的“有理数”为研究对象，从课程标准对“有理数”的要求、教材的目录、核心概念、例题、习题、旁白，以及以图形和表格为内容的非文本形式进行定量刻画与定性描述.希望对教材统计内容习题的编写和完善提供一些思考和启示.

二、研究设计

（一）教材的选取

选取中国和美国政府部门正式出版发行和使用范围较广的教科书，如表1所示：

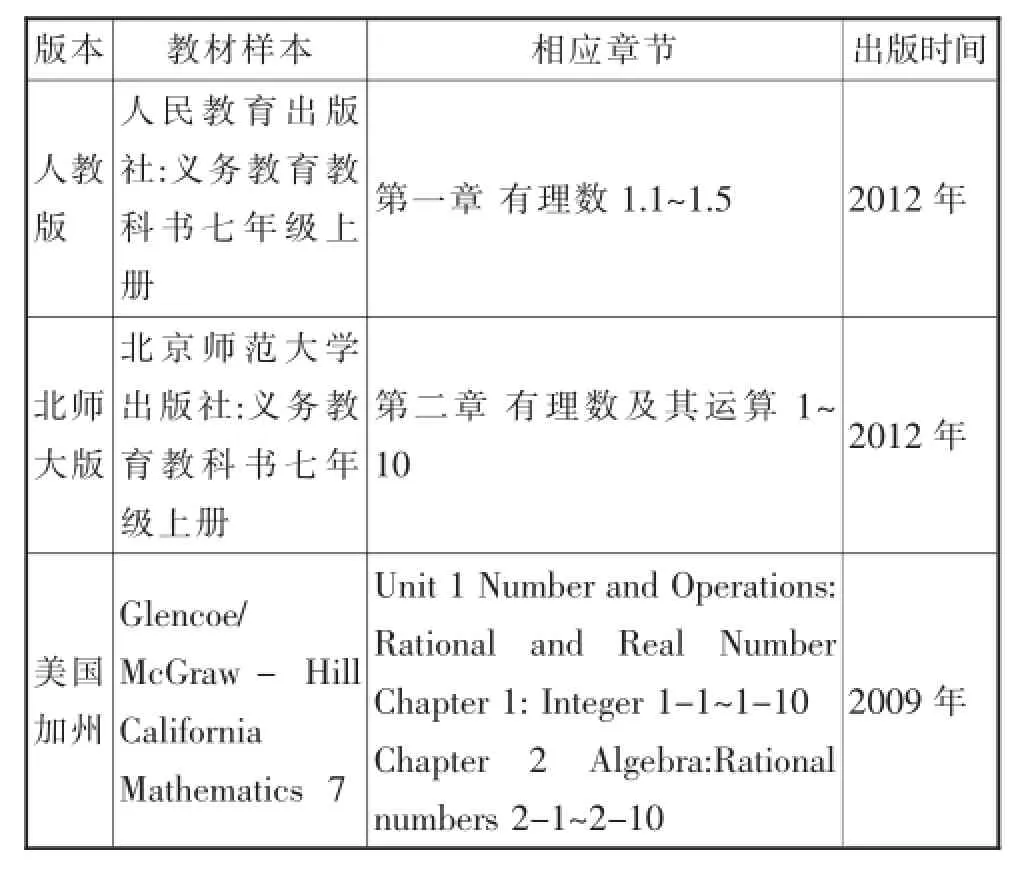
表1样本教材及其章节选取

（二）研究方法

采取定量刻画与定性描述相结合的方法.

（三）比较维度

1.三套教材整体内容的比较

美国加州教材Mathematics7第一章内容为整数，第二章为有理数，这两章完整地讲解了有理数及有理数的运算.我国人教版七年级上册第一章“有理数”和北师大版七年级上册第二章“有理数及其运算”与美国加州教材的内容相近，故这三套教材“有理数”的内容存在可比性.现将上述三个版本的“有理数”所在的章节整体结构进行对比，得到表2.

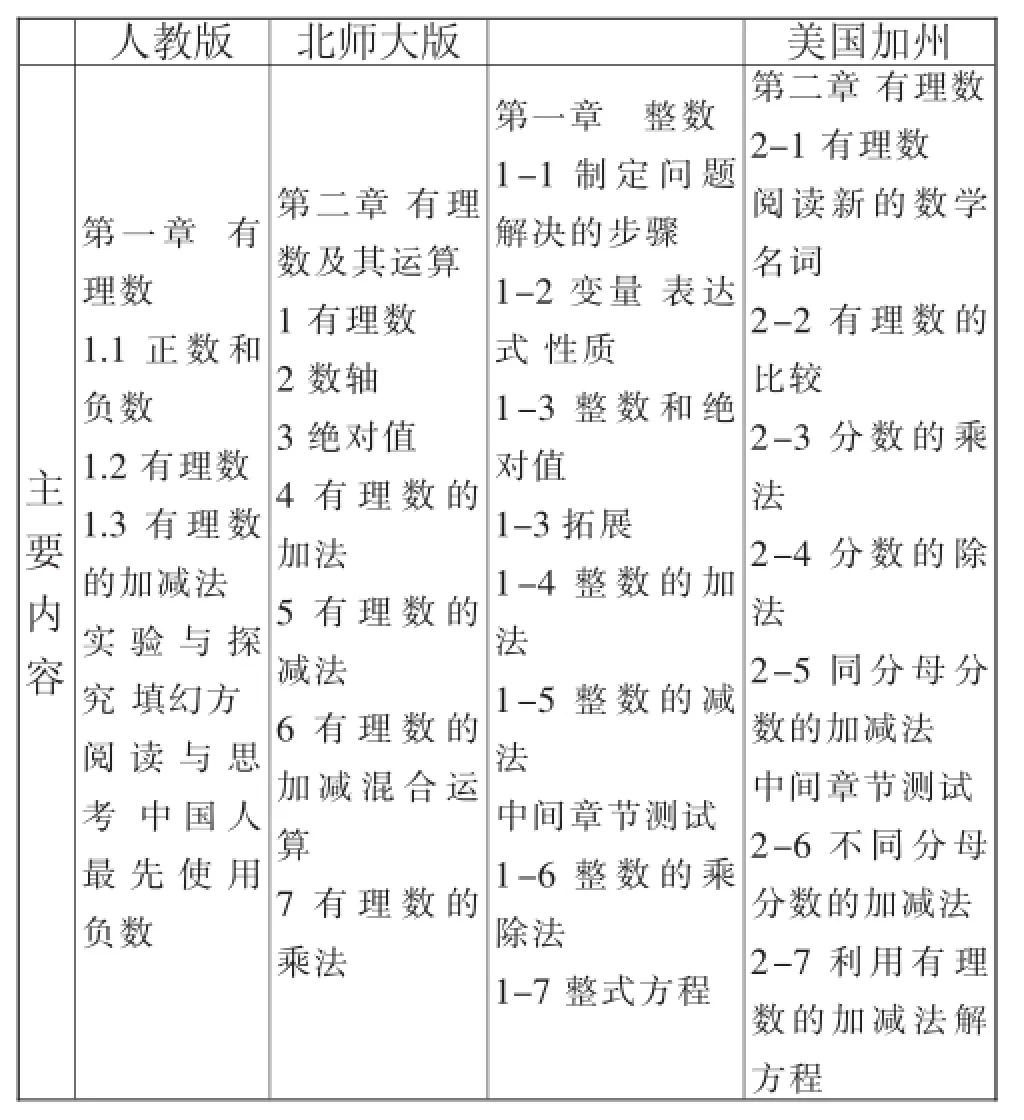
表2“有理数”及其运算的主要内容

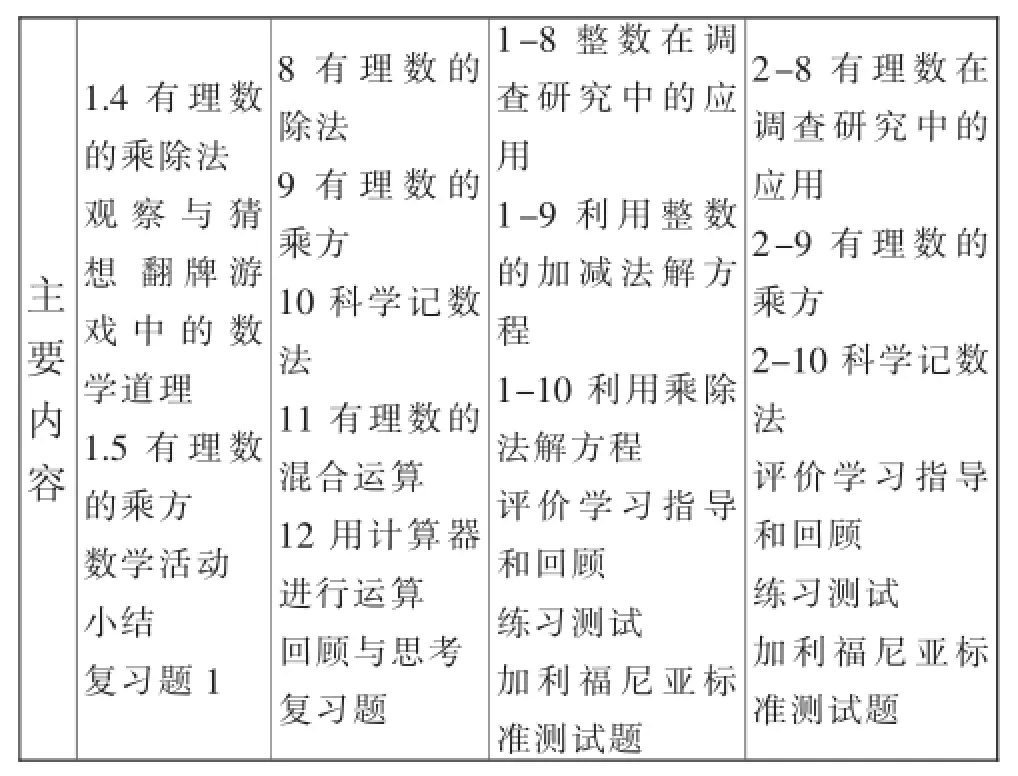
主要内容1.4有理数的乘除法观察与猜想翻牌游戏中的数学道理1.5有理数的乘方数学活动小结复习题1 8有理数的除法9有理数的乘方10科学记数法11有理数的混合运算12用计算器进行运算回顾与思考复习题1-8整数在调查研究中的应用1-9利用整数的加减法解方程1-10利用乘除法解方程评价学习指导和回顾练习测试加利福尼亚标准测试题2-8有理数在调查研究中的应用2-9有理数的乘方2-10科学记数法评价学习指导和回顾练习测试加利福尼亚标准测试题

美国加州教材将“有理数”的内容分为两章，第一章重点讲解了整数及其运算，第二章重点讲解了有限小数和分数的运算.美国加州教材对于有理数的教材设计更加符合初中生的认知结构，学生在小学已经学习了自然数和整数，在七年级引入“-”号，拓展了学生对于数的认识，第一章在学生学习整数的基础上引入负数，让学生理解负数产生的必要性，同时在整数集合内的运算也有利于学生理解整数运算的算理.这样为学习第二章的内容奠定了基础.人教版和北师大版教材都将有理数及其运算放在了一章，产生这种教材设计的原因与中美两国教材对于有理数的定义有关系，人教版和北师大版直接给出了整数和分数统称为有理数的定义，美国教材对有理数的定义是：Numbers that can be written as fractions are called rational numbers（只要能够表示为分数的数称为有理数），Since：-7可以表示为，2可以表示为，它们都是（rational numbers）有理数，所有的（integers）整数、（fraction）分数和（mixed numbers）带分数都是有理数.由于对有理数定义的不同，人教版和北师大版教材将整数和分数放在了同一章，在教学中许多老师对有理数做了进一步的定义，既有限小数和无限循环小数统称为有理数，产生这一问题的重要原因如下：在北师大版教材第二章第一节随堂练习中出现了如：3.5、-0.125、5.6这样的数，很多学生无法判断它们是否为有理数，如果以北师大版对有理数的定义出发判断，则学生没有办法把这些数归为整数和分数，那么它们为什么是有理数？所以在教学中，教师又进一步讲解如何把一个有限小数或无限循环小数化为分数，然后在利用有理数的定义将它们归在有理数的范围内，这样对学生理解水平要求很高，这也为以后学习无理数造成了一定的干扰.人教版教材中从第一节到最后一节，无论在例题、探究活动、习题、小结和复习题中都没有出现无限循环小数，对于学生理解有理数及其运算和今后无理数的学习埋下了“隐患”.

美国教材在第一章系统地讲解了整数及其运算之后，在第二章第一节给出了有理数的定义：只要能够表示为分数的数称为有理数，然后给出了大量例题和实例讲解了如何将一个分数化为小数、如何将一个有限小数和无限不循环小数化为分数，并附有大量的练习题，这为学生学习有理数及对有理数的判断扫清了障碍，如：3.5、-0.125、0.3这样的数，学生已经做了大量的训练，他们知道这些数都可以化为分数，能够精确地判断它们是有理数，从而避免了人教版和北师大版出现的问题.

美国教材在第一章和第二章中设计了有关一元一次方程的求解，主要是利用有理数的运算法则求解方程，这不仅是对有理数运算的应用，同时也是为进一步学习一元一次方程打下基础，同时美国教材在每一章中设计了对于前面内容的测试题，在章末不仅设计了本章的测试题，同时增加了对于本章内容的评价测试题，有部分题目是历年的PISSA测试题，注重知识在现实生活中的应用.人教版教材在每一章末都设计了数学活动，活动内容都和现实生活紧密联系，这也充分体现了数学知识在现实生活中的应用，体现了让每一个学生学习有价值的数学.同时也说明了学生的数学知识不仅来源于教材，也来源于学生的生活经验.

人教版教材在章末的小结中总结了有理数的运算，有利于一元一次方程的求解，同时说明由于整数可以看成是分母为1的分数，因此有理数可以表示为（p，q是整数，q≠0）的形式，这进一步拓展了对有理数概念，有利于学生对于有理数的形式理解，这和美国教材的设计内容相吻合，如图1所示.

图1美国加州教材有理数的定义

北师大版教材在章末设计了回顾与思考，提出了具体的让学生完成的内容，但是并没有明确地提出具体的做法和要求，例如，回顾与思考的7：梳理本章内容，用适当的方式呈现全章知识结构，并与同伴进行交流.在实际的教学中发现教师和学生并没有重视这部分内容，从而使得回顾与思考流于形式.人教版在利用现在的概念导图梳理了本章的知识结构，有利于学生模仿这种方法并理清知识点之间的逻辑关系.

2.数学问题情境水平分析

2016年陈志辉在《数学教育学报》中发表了《中美两国初中数学课程的问题情境水平比较研究》，文中对Stigler（1986），YepingLi（2000）等人对于教科书数学问题呈现的三个维度分析框架进行了改进，［3］如表3所示.

表3数学问题情境水平分析框架

例如，北师大版七年级上册第一章第六节中一道题目：下面是流花河水文资料（单位：m），河流的警戒水位作为0点，那么图（图略）中的其他数据可以分别记作什么？表4是小明记录的今年雨季流花河一周内的水位变化情况（上周日的水位达到警戒水位33.4米）.

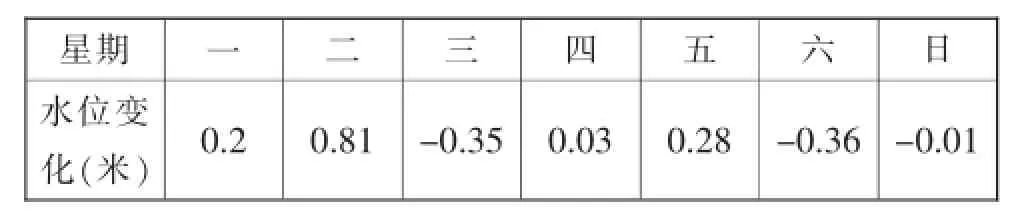
表4流花河一周水位变化表

（1）本周哪一天河流的水位最高？哪一天河流的水位最低？

（2）与上周末相比，本周末河流水位是上升了还是下降了？

（3）每天水位位于警戒水位之上还是之下？与警戒水位的距离分别是多少米？

（4）以警戒水位为0点，用折线统计图表示本周的水位情况.

依据上述分析框架，对该问题进行编码如下：首先，对情境进行判别，由于问题设计河流水位的变化，因此将该情境编码为公共情境（CL）.然后，对问题情境的三个维度进行判别：数学特征水平方面，整个问题设计有理数的加减运算，而且都属于一步运算，因此确定为水平2（OC-2）；表征特征水平方面，由于问题表述为故事情境加图表说明，因此确定其表征特征为水平4（SC-4）；任务特征水平方面，由于该情境为问题解决，所以确定其任务特征为水平3（PS-3）.

（1）数学问题情境类型比较.

两个版本中加州教材的题例（992）远远多于人教版教材（344）和北师大版教材（274），统计结果如表5所示.

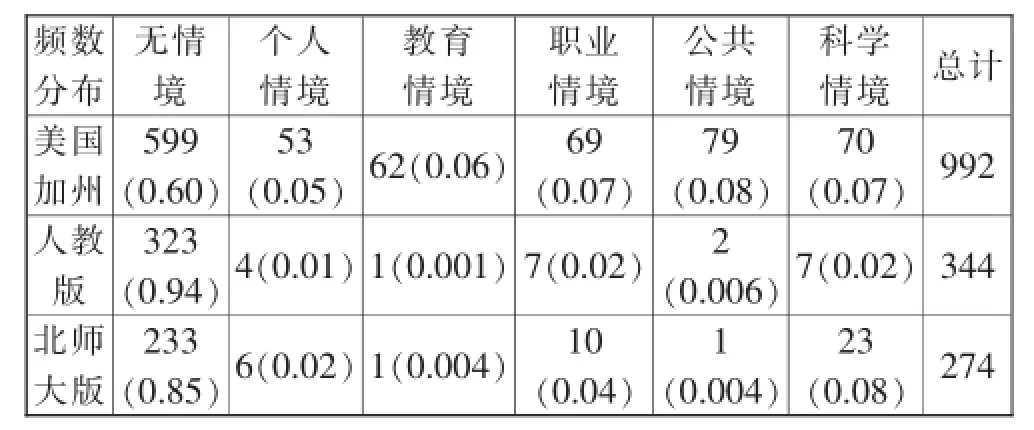
表5两国“有理数”问题情境类统计

由表5发现，美国加州教材的习题量要远远多于人教版教材和北师大版教材的习题数量，人教版无情境的题目所占比例最高，达到94%，美国加州无情境题目所占比例最低，达到60%，北师大版教材中无情境题目所占比例为85%，说明美国加州教材在题目设计时，关注题目的背景和现实生活之间的联系，将教材中的内容嵌入现实生活的各个方面.新课程标准中明确提出让每一位学生学习有价值的数学，注重学生的应用意识和创新意识，中美教材在五个情境中的题目都有涉及，但是相比之下，人教版和北师大版在这五个情境中的题目涉及相对很少，在统计中发现人教版和北师大版教材的题目大部分都是没有背景因素的纯文本的题目，而美国教材更加注重题目的现实背景.

（2）数学问题情境整体比较.

首先对三套教材的题目进行编号，然后根据表3中的数学问题情境水平分析框架开始打评分，在评分过程中反复通过论证对存在争议的题目进行再评分，保证对问题的数学特征、表征特征和任务特征所处的水平进行可靠的描述.［4］统计结果如表6所示.

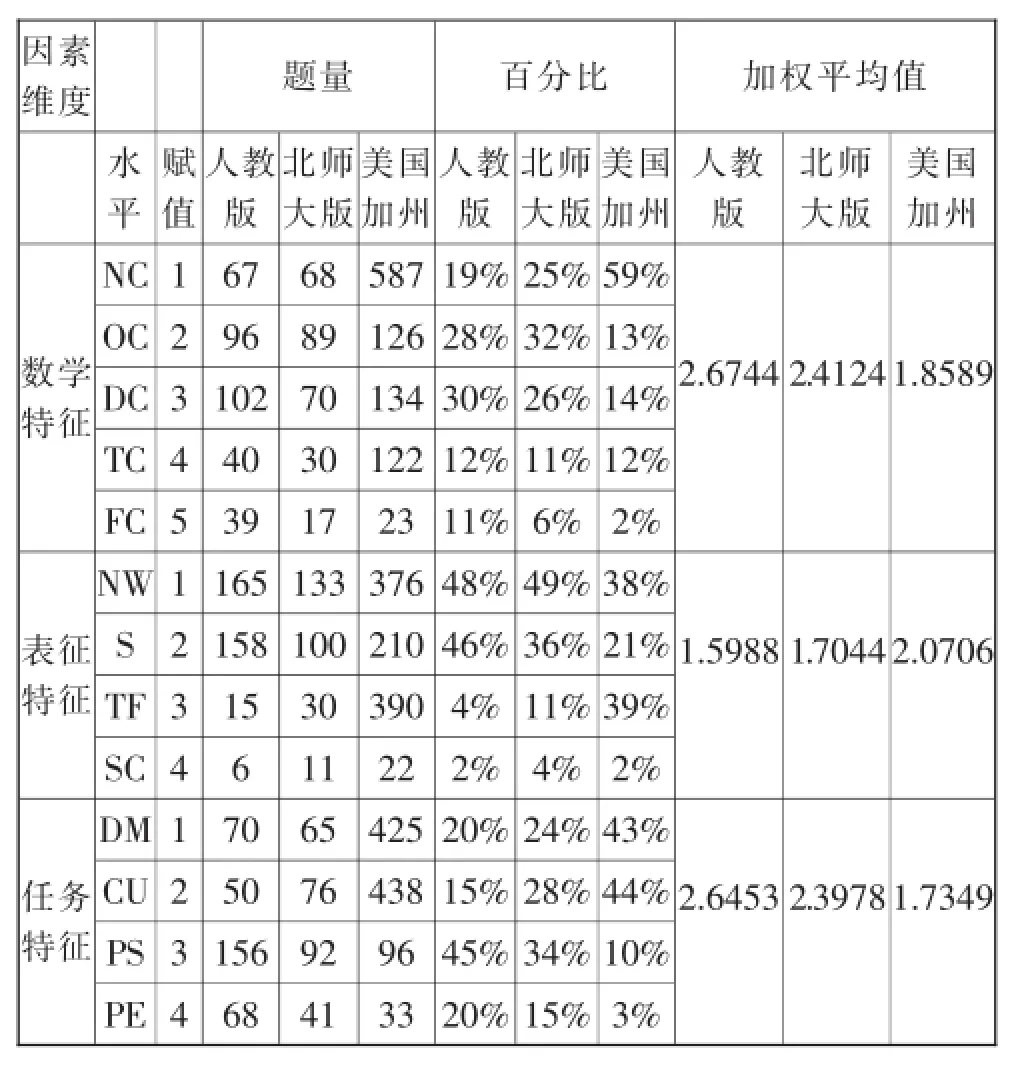
表6三套教材“有理数”内容的数学问题情境三维特征水平

表6所示，在数学特征方面人教版教材最高，其特征值为2.6744，北师大版的特征值为2.4124，美国加州教材的特征值最低，其特征值为1.8589.在表征特征方面美国加州教材特征值最高为2.0706，北师大版表征特征值为1.7044，人教版教材的表征特征值最低1.5988.任务特征方面人教版教材的特征值最高2.6453，北师大版的任务特征值为2.3978，美国加州教材的任务特征值最低为1.7349.

从横向角度比较，在数学特征方面，加州教材无运算的题目所占比例较高（59%），多步运算的题目相对较少，相反人教版和北师大教材三步运算和四步运算所占比例相对较高，分别占30%和26%，美国加州教材占了14%.在统计过程中发现美国教材对于问题设计比较细致，对于不同数学概念和数学运算的处理非常精巧，将教材内容细化为较小的知识点，针对每一个知识点设计相应的题目，在学生完成这一部分练习之后，教材中又设计相对应的提升练习，所以对于有理数的运算方面，大部分题目是一步运算和两步运算，多步运算相对较少.人教版和北师大版教材都注重对于问题的综合处理，例如，在有理数的混合运算和乘方运算中，所设计的题目都是多步运算，对学生的运算能力要求相对较高，充分体现了课程标准对于学生在运算能力方面的要求.

在表征特征方面，美国教材在图形和图表结合的水平非常高，占了39%，而人教版和北师大版只占了4%和11%，在统计过程中，发现人教版和北师大版教材中习题的呈现方式主要是以纯数字和短语的形式，大部分题目没有实际的背景和相应的图片或图表说明.2012年RaeYoungKim对三种初中年级的美国教材和韩国进行了比较，主要关注的教材中非文本因素（图案、图片、表格等）的质量在学生学习的过程中发挥作用，研究发现，教材内容中非文本因素这种可视化的表征方式，如果以恰当的方式和教材内容相结合，有利于学生对于概念的理解和问题的解决.［5］美国教材注重问题设计的背景因素，这也导致了题目呈现的方式不同，充分说明美国学生利用可视化表征方面的能力较高.

在任务特征方面，人教版教材在“问题解决”和“问题探究”的水平最高，分别占了45%和20%，北师大版在这两个方面的水平分别为34%和15%，美国教材在这两个方面的水平最低，只占了10%和3%，美国教材习题的设计主要考查学生对于教材中概念的理解，所以在“概念性理解”的水平最高，占了44%，而人教版和北师版在“概念性理解”的水平则较低，分别占了15%和28%.在统计中发现美国教材在课后习题中明确标明这道题目所涉及的数学概念和运算法则，在教材旁白中也明确标明题目所对应的章节和概念，在章节的开头和末尾都将本章出现的新的数学名词加以强调和解释，有的概念采用不同的方式进行阐释，例如：有限小数、无限循环小数.而人教版和北师大版则更加注重有理数相关概念的理解和法则的应用，这也体现了我国对于中学生解决问题能力方面的要求，反映了两国课程不同的要求.

三、结论与启示

在“有理数”内容的编排方面，美国加州教材将“有理数”部分分为两章，第一章专门讲解了整数及其运算，第二章主要讲解有理数、分数、小数等概念和运算.人教版和北师大版则将“有理数”设计为一章，但是在具体内容的编排上也是先呈现整数的有关运算，然后是分数和小数的运算，这也符合学生的认知水平和数学学习的心理水平；在有理数这个核心概念的表述方面，两国教材也存在很大差异，人教版和北师大版的表述是一致的，既整数和分数统称为有理数，而美国加州教材的表述是：只要能够表示为分数的数称为有理数，相比之下，美国加州教材对于有理数定义的表述更加科学合理；在比较中发现美国加州教材对于基本概念阐述非常清楚，例如，教材中专门对于整数、分数、有限小数、无限循环小数、有理数等新的概念做了详细的定义和解释，对于每个知识点讲解非常详细，而且每节内容所包含的信息量非常大，题目设计丰富多彩，题目的个数也非常之多.而人教版和北师大版对于整数、分数、有限小数、无限循环小数、有理数等基本概念并没有过多的解释，只是举了几个具体的例子，在教学中发现，学生并不能很好地理解这些看似简单的概念.在教材旁白方面，美国教材每节课都在教材的左侧空白出呈现出学完本节课要达到的学习目标，同时附有这节课学习的网络资源，对于本节课的重点内容都有学习的提示和建议（studytip），便于学生模仿和参考.而人教版和北师大版在教材旁白方面则做的比较少，很少有某个具体问题的解释和补充.

在问题情境水平的比较，三套教材各具特色.在数学特征方面，人教版和北师大版注重学生的多步运算能力，数学问题的难度相对较高.相比之下，美国加州教材则更注重基本运算能力，问题相对小而精，便于学生运算，所以问题也非常之多.在表征特征方面，加州教材更加注重非文本内容和文本内容结合的呈现方式，题目设计灵活多样，背景内容丰富多彩，紧密贴近现实生活，紧跟时代发展脚步，这种可视化的表征方式有利于学生对于具体问题的理解和解决，有利于培养学生对于现实问题的兴趣，提高他们的创造力.而人教版和北师大版教材中习题的呈现更多的是文本内容，大部分题目都是纯数学符号和文字的描述，关注学生的符号意识，注重学生的具体运算和抽象运算.在任务特征方面，人教版和北师大版教材习题都注重学生解决问题的能力，而美国加州教材则更加关注学生对于基本概念的理解和掌握，没有过多的综合问题和复杂问题.

通过对三套教材定性与定量的分析，给我们得到如下启示：首先，中国教材过多地注重学生的练习和复杂问题的解决，而并不关注对于教材中核心概念的理解和掌握.［6］～［8］在教学中教师更多地注重题目的大量重复的练习和巩固，而忽视了学生对于问题本身的理解和感悟.其次，在数学问题的表征方面，习题设计过于死板，表征特征方式单一，没有挖掘知识的相关背景，问题设计缺乏情境，忽视了可视化表征的影响，造成问题解决和现实客观之间的差距.最后，数学教学是一种感悟教学，要让学生悟其道，之后才可以行之远，关注问题的内涵设计，例如，关注学生的灵魂设计，关注问题的情境设计如关注学生的情感设计，关注教材的精细化设计（如关注学生的骨骼设计），从而更好地服务于每一个鲜活的精灵.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.曹一鸣，王竹婷.数学“核心思想”代数思维教学研究［J］.数学教育学报，2007（1）.

3.陈志辉.中美两国初中数学课程的问题情境水平比较研究——以“函数”内容为例［J］.数学教育学报，2016（1）.

4.鲍建生.中英初中数学课程综合难度的比较研究［M］.南宁：广西教育出版社，2009.

5.Rae Young Kim.The quality of non-textual elements in mathematics textbooks：an exploratory comparison between South Korea and the United States［J］.ZDM-Mathematics Education，2012（2）.

6.杨慧娟，裴昌根.60年来初中数学教材编写的历史沿革与启示——以人教版为例［J］.数学教育学报，2011（2）.

7.顾继玲，张新华.初中数学教材探究活动设计的思考［J］.数学教育学报，2012（3）.

8.曹一鸣，吴立宝.初中数学教材难易程度的国际比较研究［J］.数学教育学报，2015（4）.H