将建模意识培养贯穿于知识发展过程中——以“多边形的内角和”为例

☉江苏如皋高新区实验初中殷瑾

将建模意识培养贯穿于知识发展过程中——以“多边形的内角和”为例

☉江苏如皋高新区实验初中殷瑾

数学模型是学生分析和解决数学问题的重要工具，具有较强的建模意识将有利于学生从复杂的问题情境中抽取数量关系，找寻问题解决的路径.在初中阶段，很多教师将培养学生的建模意识作为自己教学一项重要任务在基础知识教学中加以落实，取得了很好的效果.现结合“多边形的内角和”的教学，谈谈这些老师的做法，希望能给您带来启示.

一、新知教学：从公式到方程

新知教学是数学教学的重要内容.初中阶段的每一次新知教学几乎都会蕴含一些数学模型.因而，获取及应用新知的过程也就成为了培养学生建模意识的过程.

案例1：“多边形的内角和”新知探究.

教师引导学生通过构造不同的辅助线将多边形分成若干个三角形，进而得出多边形的内角和计算公式：W=180°（n-2）.接下来，教师提问：在这个公式中有几个未知数？（2个）如果给你一个未知数的值，这个公式变成什么了？（方程）在学生给出结论后，教师投影例题.

例题：一个多边形的内角和是1980°，求它的边数.

学生自主解答，然后在小组和全班进行交流.最后，教师就怎样由公式出发建构方程模型进行了总结.

简析：在多边形的内角和教学中，师生经历由特殊到一般的认知历程后，获得了内角和公式，这个公式实际上是一个函数模型.教师针对公式的追问：“这个公式中有几个未知数”，将函数思想渗透其中；“如果给你一个未知数的值，这个公式变成什么了”，让学生初步感知到了“两个未知数”向“一个未知数”转化带来的丰硕成果——方程，这是学生已经学过的知识，新的问题，熟悉的模型，这是认知的自然回归.接下来的自主训练和互动交流，将方程模型的应用变为现实，学生在问题解决过程中，充分感知了“由公式到方程”的转化历程，获得了体验，积累了经验，同样也提升了分析和解决问题的能力.

二、对比练习：从个性到共性

对比练习，是指教师将一些蕴含相同或相近数学模型的问题放在一起，在集中解答交流中培养学生利用同一数学模型分析和解决问题能力的过程.对比练习，一般不超过三题为宜，出现时机在学生获取新知后最佳.

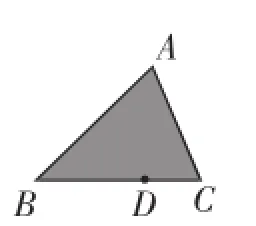
图1

案例2：“多边形的内角和”巩固练习.

在学生获得多边形内角和公式并进行简单巩固后，教师引导学生通过计算推理得出“多边形的外角和为360°”的结论.在接下来的巩固练习中，教师呈现了如下题组.

（1）一个多边形的每个外角都是30°，则它是___________边形.

（2）如图1，一块实验田的形状是三角形（设其为△ABC），管理员从BC边上的一点D出发，沿DC→CA→AB→BD的方向走了一圈回到D处，则管理员从出发到回到原处在途中身体（）.

A.转过90°B.转过180° C.转过270°D.转过360°

（3）一只蚂蚁从A点出发向前走5cm，向左转45°，继续走5cm，再左转45°，它以同样的走法第一次走回A点时，共走了________cm.

学生自主解答，教师巡视指导. 5分钟后，教师让学生展示了自己的结果及获得结果的过程，在不断强化对“多边形的外角和为360°”这一结论认知的同时，将三个问题解决过程中都涉及的图形模型展示在黑板上，如图2.

图2

简析：教学“多边形的外角和等于360°”，我们不能仅仅把它当作一个文本结论，还要关注与这一文本高度关联的图形模型，这是学生化解很多数学问题的基本模型.所以教师在学生获得文本结论后，通过三个题目的练习与交流，凸显了图形模型的作用和价值：题（1）只需用文本结论即可求解，题（2）在建构外角的情况下用“多边形的外角和为360°”，题（3）在将信息转化成外角和后同样需要借助图形来理解“多边形的外角和为360°”.这三个简单的看似有所区别的模型，实则其指向是一致的，都指向了图形，这与教者最终归纳出具有共性特征的模型是完全一致的.

三、综合训练：从单一到关联

建模意识的培养，我们要关注单一数学模型的建构，同时，还应关注不同模型之间的转化和关联.一方面，可以为学生提供不同的分析和解决问题的路径，另一方面，能够不断提升学生的建模能力，将知识向能力转化.

案例3：“多边形的内角和”训练提升.

新知教学及例题讲评结束后，教师安排了如下综合训练.

（1）若一个多边形内角和等于其外角和的3倍，则这个多边形是_______边形.

（2）若一个多边形除了一个内角，其余各内角之和是2570°，则这个角是______.

学生自主解答，5分钟后，教师组织学生进行小组交流和全班交流.

对于题（1），教师引导学生从不同的角度给出解题思路：根据“内角和是外角和的3倍”，得出内角和为1080°，进而用方程求解；根据“内角和是外角和的3倍”和“一个内角和其相邻的外角互补”得出这个多边形的每一个内角为135°，列方程135n=180（n-2）求出边数；根据“内角和是外角和的3倍”和“一个内角和其相邻的外角互补”得出多边形的每一个外角为45°，利用外角和直接求得边数.

对于题（2），由于绝大多数学生是通过算术的方法估算边数的，所以教师引导学生通过列不等式组求解.

简析：在学生获得“四基”过程中，教师有一个重要的任务是帮助学生建构有效的知识网络，促进其知识的系统化.在“训练提升”环节，教师将一些本课的或与本课知识有关联的数学模型隐藏到两道数学题中，以解答和交流直观展示其生成和应用过程，进而培养学生应用数学模型解决数学问题的意识和能力.

数学模型，来自于学生获取数学知识和应用知识的过程之中，这个过程实际上也是数学知识生成和发展的过程.所以培养建模意识应与数学知识的发展进程紧密契合.作为一线教师，我们所要做的就是：在知识生成过程中，让学生抽象出数学模型；在知识的简单应用过程中，提炼共性特征，呈现应用范围较大的数学模型；在综合训练中，将数学模型关联起来，促进模型的网络化.总之，应用数学模型化解数学问题的意识并不是一时半会就能养成的，这需要教师能时刻关注模型的建构与应用，将它们安放在学生的视野中，以有效的练习与交流促进学生的发展.Z