遵循问题的本源，提高教师的素养——2016年广州市数学中考第25题思维突破与教学启示

2016-12-07广东东莞中学松山湖学校张青云

中学数学杂志 2016年18期

关键词：托勒密本源勾股定理

☉广东东莞中学松山湖学校张青云

☉广东东莞市教育局教研室刘翥远

遵循问题的本源，提高教师的素养——2016年广州市数学中考第25题思维突破与教学启示

☉广东东莞中学松山湖学校张青云

☉广东东莞市教育局教研室刘翥远

2016年广州市数学中考第25题是一道很有见地的试题，有关它的讨论曾在一些QQ群里热度不减.笔者也很关注这道试题，在此特作一梳理，并提出自己的一些思考，供大家研究参考.

试题：如图1，点C为△ABD外接

（1）求证：BD是该外接圆的直径；

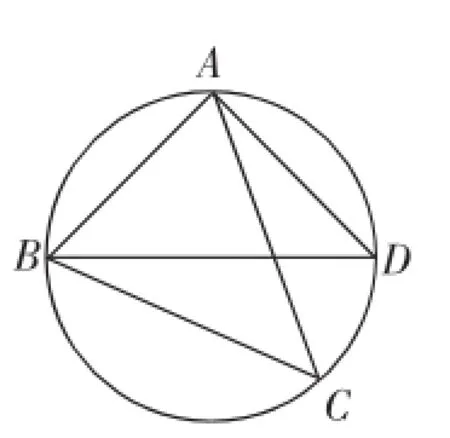
图1

（3）若△ABC关于直线AB的对称图形为△ABM，连接DM，试探究DM2、AM2、BM2三者之间满足的等量关系，并证明你的结论.

一、思维突破

（1）由同弧可知∠ADB=∠ACB.又∠ACB=∠ABD= 45°，则∠BAD=90°.由圆周角定理的推论不难得到BD是该外接圆的直径.

（2）从证明结论上看，本小题似乎不太容易，但实际上证明方法很多.由AC或由结论变化得的形式，联想到等腰直角三角形三边的比为1∶1，可以尝试构造合适的等腰直角三角形，下面我们沿着这种思路介绍两条路径.

路径1：构造以BC、DC为斜边的等腰直角三角形.

如图2，作BE⊥AC于点E，DF⊥AC于点F.由∠ACB=∠ADB=∠ABD=∠ACD=45°，可以得到△ABD、△CBE、△DFC都为等腰直角三角形.

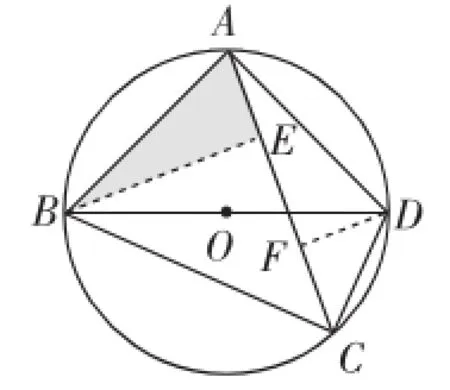
图2

由已知不难证得△ABE≌△DAF，则AE=DF.

路径2：构造以AC为直角边的等腰直角三角形.

以AC为直角边的等腰直角三角形，意味着直角三角形是以点A或点C为直角顶点.由于等腰三角形的“朝向”分布的不同，还可以产生以下四种可能的图形，如图3，但其实每一种都可以达成目的.在此我们选择第一种情形简述.

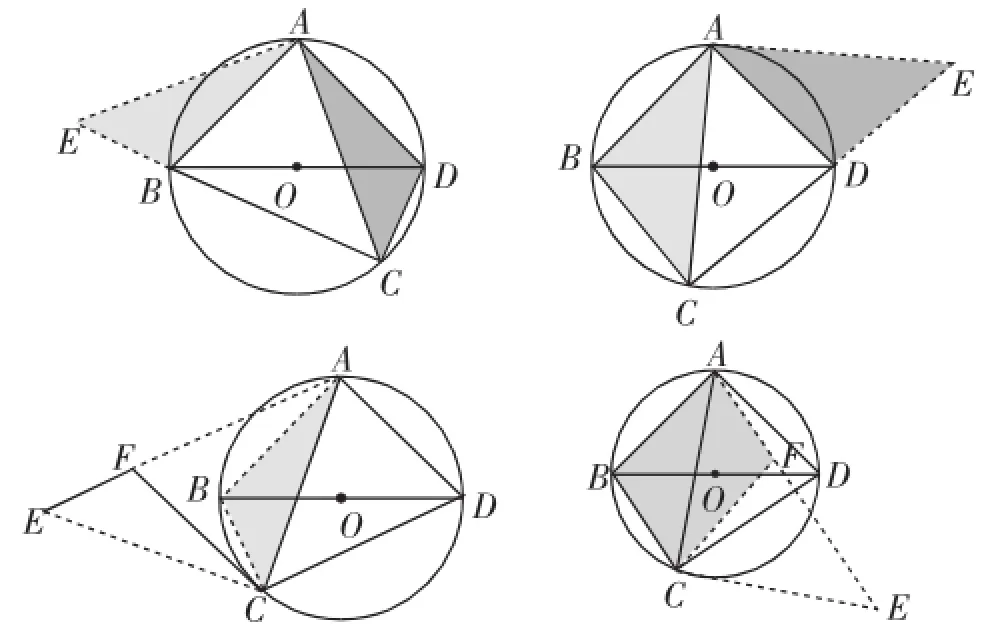
图3

如图3，作CA⊥AE，延长CB交AE于点E.由∠ACB= 45°可知△ACE为等腰直角三角形，则CE=AC.由SAS可证明△ABE≌△ADC，则BE=DC.则CE=BE+BC= DC+BC=AC.

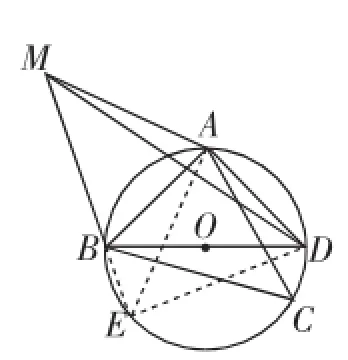
图4

（3）本小题当然最有挑战.三线段的平方容易使人联想到勾股定理，所以解题的关键在于努力构造直角三角形.

思路1：考虑选择三线段中的最长线段DM为斜边，构造直角三角形，如图4，延长MB交圆于点E，连接AE、DE.

由BD为直径，得∠BED=90°.则ME2+DE2=MD2.

由∠BEA=∠ACB=∠BMA=45°，可推得△MAE为等腰直角三角形，则ME2=MA2+AE2=2MA2.

由AC=MA=AE，∠MAB=∠CAB=∠EAD，根据弧、弦、圆心角定理或三角形全等可证明DE=BC=MB，所以2MA2+MB2=MD2.

思路2：将线段DM利用旋转变换，如图5，过点A作AE⊥AC，延长CD交AE于点E，连接BE.

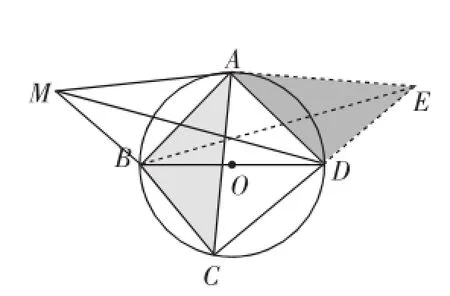
图5

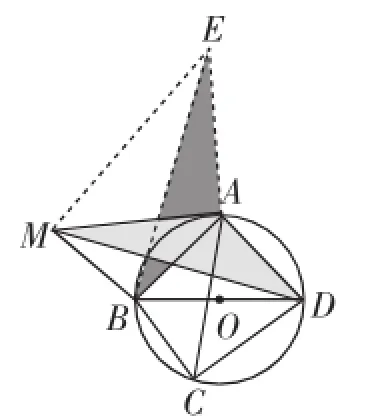
图6

易证△AMD≌△AEB，则MD=BE，然后在Rt△BCE中运用勾股定理，通过变换可得到相同的结论.

图6也是类似的旋转变换，在Rt△BME中运用勾股定理.

至于有网友使用余弦定理或正弦定理等，通过恒等变换得到问题的结论，由于超出了初中学生的学力范围，在此不作推介.

二、教学启示

1.对试卷压轴题的难度梯度做到知己知彼

本试题作为广州试卷的压轴题，带有明显的区分度特征是理所当然的，特别是在今年广州数学试卷整体表现平稳的情况下，本试题的选拔意味就更趋强烈，但既使这样，依然存在着较大的可为空间，比如第一问对多数学生来说应当问题不大，第二问应当也有不少的学生可以解决.阅卷中发现，很多同学在第二小题便遇到了障碍，询问其原因，认为“所证结论不太常见，一时半会想不到”“没时间细看”等占有很大比例，于是在“争分夺秒”的考场上，眼见所剩时间无几，便选择“战略性放弃”.这启发我们在教学中，应明确告知学生压轴题设置的常见方式与各小问的难度梯度，并借助一定的典型示例训练感悟，把握各小问的难度分配，以做到知己知彼、有的放矢，增强攻克难关的自信.

2.思考要遵循问题的本源

本试题的（2）、（3）较难，但再难的问题也要遵循本源去思考.遵循问题的本源，就是让解法自然产生，也就是从问题的结论或条件出发，自然而然地追寻解决之路径.第二问的本质是证两条线段的和等于另一条线段的问题，难点在于也罢，关键是要将它们转化为新的线段，由题目中丰富的45°，很自然地联想到构造等腰直角三角形，利用其三边关系转化为“a=b+c”型证明问题，再运用“截长补短”的全等思想方法来解决问题.第三问虽然难度较大，但仍然要凭着对勾股定理的直觉思维，围绕DM来思考，构造以DM或者旋转后DM的等长线段为斜边的直角三角形.当然，由结果回溯，我们依然看到了各小问之间千丝万缕的联系，所以这种思考问题的方法就是自然解法，即在正常情况下首先想到的思路和解法.所谓“道法自然”，教学中就是要遵循这种解题思想和策略，从解决问题最自然的思路出发，“顺理成章”地往思维更高处延伸.

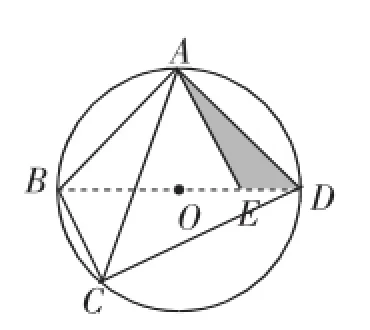
图7

3.丰富自己的学科知识

有一定学科知识的教师应该知道，本题第二问的实质是托勒密（Ptolemy）定理的特殊情况.托勒密定理：圆的内接凸四边形两组对边乘积的和等于两条对角线的乘积.以图7为例简证如下.

在对角线BD上找一点E，使∠DAE=∠CAB，则可得到∠BAE=∠CAD，进一步可推得△AED∽△ABC，△ABE∽△ACD，分别得到比例式：

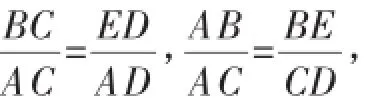
即BC×AD=AC×ED，AB×CD=AC×BE.

两式相加可得：

AB×CD+BC×AD=AC×BE+AC×ED=AC×BD.

本试题的第二问为其特殊情况，即AB=AD，且∠BAD=90°，则BD=AB.则AB×（CD+BC）=AC×BD.化简得到：BC+CD=AC.

这个定理，最初是由古希腊数学家克罗狄斯·托勒密（公元90年—公元168年）想出来的，所以叫作托勒密定理，其逆定理也成立.托勒密是一位博学多才的古希腊天文学家、地理学家、占星学家和光学家，就是他，在其著作《天文学大成》中构造了一个“地心说”的“完整”体系，被中世纪的西方世界尊崇为天文学的标准著作，影响长达13个世纪，同时，这本著作也为三角学的进一步发展与应用奠定了坚实的基础.托勒密定理的价值是不可估量的，从它出发可以推导出正弦、余弦的和差公式及一系列的三角恒等式，并以此为基础，托勒密给出了从0°到90°每隔15′角的正弦值，创造出了世界历史上的第一张弦表.

这个定理在以前的人教版教材中是有渗透的，在一些初中数学竞赛的书籍中也有介绍，现在则是作为普通高中数学选学教材的一个内容呈现，在新课程改革背景下，它逐渐淡出了我们的视野，久而久之，渐为人所遗忘.笔者认为，不教不学的，并不表示可以不知不晓.作为初中数学教师，我们要不断提高自己的学科素养，尽力防止自己的学科知识随着岁月的流逝而萎缩，坚持保有足够丰富的学科视野，唯有这样，方能在教学中真正做到深入浅出、有的放矢.