反思考题难点，预设“一题一课”——以2016年江苏南通中考卷第28题为例

☉江苏省海安县李堡初级中学朱国生

反思考题难点，预设“一题一课”——以2016年江苏南通中考卷第28题为例

☉江苏省海安县李堡初级中学朱国生

近读《中学数学》（下），不少老师围绕2016年中考试题给出思路突破，并设计“一题一课”，感觉十分实用，可以直接拿到课堂上去开展教学.加上笔者有机会参加了2016年南通市中考阅卷，承担了全卷最后一题的评分工作，对众多考生解答考题的方法有了较为全面的关注，阅卷之后，将该题的思路突破和讲评的教学构思整理出来，提供研讨和分享.

一、考题的思路突破与解后反思

考题（2016年江苏南通中考卷第28题）如图1，在平面直角坐标系xOy中，点C（3，0），函数y=（k＞0，x＜0）的图像经过▱OABC的顶点A（m，n）和边BC的中点D.

（1）求m的值；

（2）若△OAD的面积等于6，求k的值；（3）若P为函数y=（k＞0，x＜0）的图像上一动点，过点P作直线l⊥x轴于点M，直线l与x轴上方的▱OABC的一边交于点N.设点P的横坐标为t，当=时，求t的值.

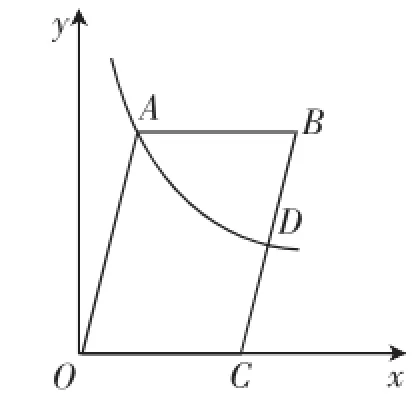
图1

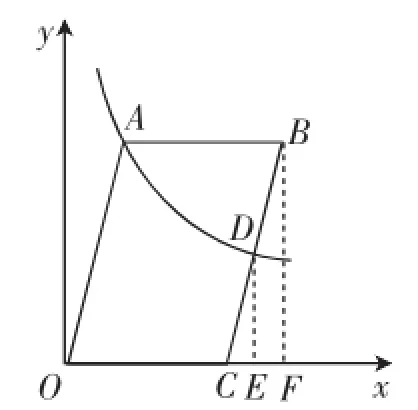
图2

1.思路突破

（1）先设法用m、n表示出点B的坐标为（m+3，n）；再设法表示点D的坐标，如图2，过点D作DE⊥x轴于点E，过点B作BF⊥x轴于点F，借助△CED∽△CFB，可得==，再结合D为BC的中点，CF=m，BF=n，有CD=CB，CE=，DE=，于是D（ 3+，）.因为点A、D在函数y=的图像上，可得mn=（3+）·=k，这里虽然参数较多，但可消去n，解得m=2.

（2）如图3，首先要回顾一个平行四边形的面积性质，即△AOD的面积应该等于▱OABC面积的一半，这样可得▱OABC的面积为12；接着用n的代数式表示出▱OABC的面积，从而得到关于n的方程，即S▱OABC=OC· yA=3n=12，解得n=4，所以A（2，4），即k=2×4=8.

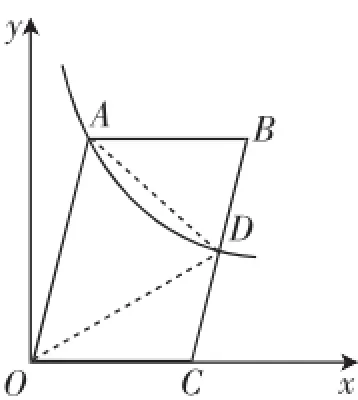
图3

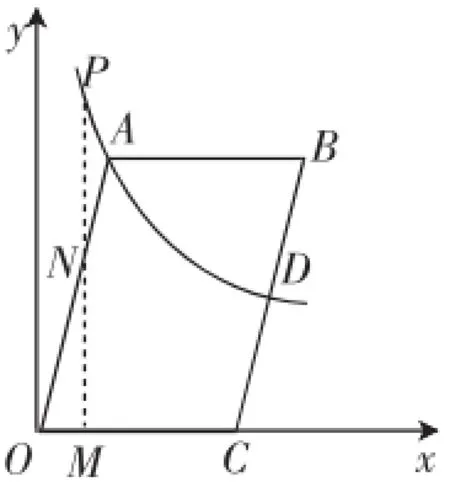
图4

（3）先做些准备工作，结合点A的横坐标为2，利用反比例函数关系式用含k的代数式分别表示点A（ 2，），B（ 5，）.由于点P的横坐标为t，可用t的代数式表示点P的坐标和PM的长，即点P在函数y=的图像上，可得

接下来，根据点N的位置情况分在OA边上、AB边上、BC边上讨论，构造如图4～图6的示意图进一步分析.

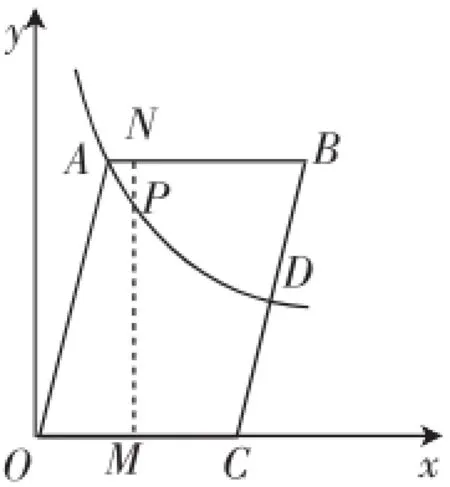
图5

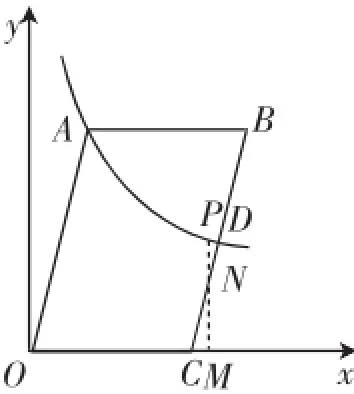
图6

2.解后反思

以下从该题的主要难点给出几点反思.

难点之一：起点较高，需要较强的变形、消元能力.

第（1）问有多个参数m，n，k，不容易看穿问题的结构，只能构造图2，利用相似三角形的性质用含m、n的式子表示出点D的坐标，并根据A、D同时在反比例函数图像上列出含m、n、k的等式，然后逐个消元，消去k、n，可求出m.注意：也只能求出m，即不能确定n、k的值.

难点之二：平行四边形面积的深刻理解与灵活运用.

第（2）问的关键是认识图3中△AOD的面积应该等于▱OABC面积的一半，然后得出▱OABC的面积为12；这对于后续用含n的式子来表示▱OABC的面积有重要作用.根据阅卷发现，一个易错点是，不少学生虽然第（1）问没有解出，但却可以解出第（2）问，而把第（2）问解出的n回代第（1）问后，再求出m的值，这种解法是有漏洞的，阅卷时第（1）问并不能得到满分，属于交叉引用题肢中的条件.

难点之三：制定合理分类标准使问题不重不漏.

第（3）问在“准备工作”（用含k、t的式子表示相关点或线段的坐标）之后，一个重要进展就是合理制定分类标准，即分点P在三条不同边上进行讨论，在边BC上，还需要进一步“二级分类”，即思考点P在N点的上方或下方时，列式时用“”来统一，以防漏解.

二、解题教学的“微设计”

教学环节一：熟悉图像，热身问题

（1）求k的值；

（2）求点D的坐标；

（3）求▱OABC的面积；

（4）求△AOD的面积.

设计意图：通过赋值点A的坐标，从特殊出发，引导学生先熟悉图1中的一些线段之间的关系，坐标之间的灵活转换，为后续问题的探究热身.

教学环节二：考题探究，铺垫问题

例2如图1，在平面直角坐标系xOy中，点C（3，0），函数y=（k＞0，x＜0）的图像经过▱OABC的顶点A（m，n）和边BC的中点D.

（1）用含m、n的式子表示点D的坐标.

（2）求m的值.

（3）小琪同学经过探究，发现点A一定在直线x=2上.你觉得小琪的发现正确吗？为什么？

（4）求证：点B一定在直线x=5上.

（5）连接AD，OD，△AOD与▱OABC的面积有什么数量关系？为什么？

（6）在（5）条件下，若△OAD的面积等于6，求k的值.

设计意图：通过增设第（1）问，促进学生自主发现点A的横坐标m，增设第（3）问服务于第（4）问求k的值.

教学环节三：考题探究，铺垫问题

例3如图1，在平面直角坐标系xOy中，点C（3，0），函数y=（k＞0，x＜0）的图像经过▱OABC的顶点A（2，n）和边BC的中点D.若P为函数y=（k＞0，x＜0）的图像上一动点，过点P作直线l⊥x轴于点M，直线l与x轴上方的▱OABC的一边交于点N.

（1）用含k的式子表示点A、B、D的坐标；

（2）设点P的横坐标为t，用含t、k的式子表示点P的坐标及PM的长；

（3）当点N在边AB上，且PM=PN时，求点P的坐标；

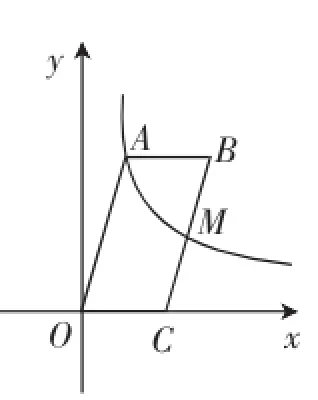
图7

教学环节四：听课检测，变式再练

改编题：如图7，在平面直角坐标系xOy中，点C（4，0），函数y=（k＞0，x＜0）的图像经过▱OABC的顶点A（m，n）和边BC的中点M.

（1）用含m，n的式子表示点M的坐标.

（2）求m的值.

（3）若点B在直线x=a上，求a的值.（4）设直线x=t与函数y=（k＞0，x＜0）的图像交于点P，与▱OABC在第一象限的边交于D点，与x轴交于E点.

①当PD=PE时，求t的值；

改编意图：改编了数据和字母，并且增设了一些铺垫问题，有效检测听课的效果，根据教学经验，如果学生真正理解了考题及上面的讲评过程，那么该变式习题也可以找到类似的解答方法.

三、结束语

笔者以为，“一题一课”的研究是一个很大的课题，特别是对于复习课、较难的综合题讲评课，有着特殊重要的现实意义.不仅仅为了学生的“眼前利益”，更重要的是传递学生研究综合题的探究套路，从简单出发，明晰起点，看准方向，锲而不舍，勇攀高峰，挑战自我.在这个意义说，“一题一课”的研究方兴未艾，期待看到更多的案例跟进，丰富这个课题的案例成果.

1.郑毓信．数学方法论入门［M］．杭州：浙江教育出版社，2006（3）.

2.罗增儒．数学解题学引论［M］．西安：陕西师范大学出版社，2008．

3.【美】波利亚，著.怎样解题［M］．阎育苏，译．北京：科学出版社，1982.

4.杨卫东．客从何处来：一道几何把关题的命制历程［J］．中学数学（下），2016（8）．H