逆向思考探新知，殊途同归求简化——以“平行四边形的判定”教学为例

☉江苏省淮安市开明中学韩建

逆向思考探新知，殊途同归求简化——以“平行四边形的判定”教学为例

☉江苏省淮安市开明中学韩建

平行四边形的性质与判定可以看成是条件与结论转换后的互逆命题（互逆定理），开展平行四边形的判定的教学研讨可以认真分析知识生长点，即引导学生将平行四边形的性质“逆过来”思考，逐一得出平行四边形的判定，这样的知识生成是自然的，本文记录近期笔者执教该课时的教学简录，并给出教后反思，提供研讨.

一、“平行四边形的判定”教学简录

1.复习旧知，引入新课

师：上节课我们学习了平行四边形，怎样的四边形称为平行四边形呢？

生：两组对边分别平行的四边形叫作平行四边形.

师：这句话可以作为定义，还可以作为什么呢？

生：它不仅是定义，还是一条性质，还可以作为判定.

师：平行四边形还有哪些其他性质？（在学生回答的基础上在黑板上列出下表）

平行四边形的性质平行四边形的对角相等平行四边形的邻角互补对角线平行四边形的对角线互相平分平行四边形的对边平行平行四边形的对边相等角边

师：今天我们来学习平行四边形的判定.（课题）

2.数学实验，探究新知

师：每位同学桌上已经准备了两根牙签和两根棉签.你能在平面内将它们首尾顺次相接，组成一个平行四边形吗？同学们动手试试看.请生1到台前来操作.

师：请你告诉大家，你是如何拼接的？

生1：把两根牙签和两根棉签分别作为四边形的对边.

师：也就是说，你认为如果一个四边形有两组对边分别相等，那么这个四边形是平行四边形？

师：我们得到了这样一个命题：两组对边分别相等的四边形是平行四边形.这是一个真命题吗？

生众：是的.

师：怎么才能说明这是个真命题呢？

师：证明之前，我们要做些什么准备工作？

生2：根据命题画出图形，写出已知和求证.

师：已知和求证如何来写？

生3：已知：如图1，在四边形ABCD中，AB=CD，AD= BC.求证：四边形ABCD是平行四边形.

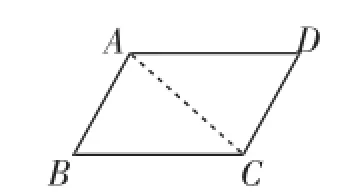
A D B C

师：现在，我们有没有方法来证明这是一个平行四边形呢？

生4：可以根据定义来证明.

师：很好.请说说你的证明思路？

生4：连接AC，证明△ABC≌△CDA.

师：好，下面请大家写出证明过程.

师：这样我们就得到了第二个判定平行四边形的方法，作为判定定理1：两组对边分别相等的四边形是平行四边形.

符号语言描述：因为AB=CD，AD=BC，所以四边形ABCD是平行四边形.

填表：

师：它们之间有什么样的关系？

生5：它们是互逆的.

师：你还能猜想出其他的判别方法吗？

生6：两组对角分别相等的四边形是平行四边形.生7：对角线互相平分的四边形是平行四边形.师：非常好！要说明它们能否作为平行四边形的判定方法，我们就要一一验证.

我们先看生6提出的“两组对角分别相等的四边形是平行四边形”.

命题：两组对角分别相等的四边形是平行四边形.已知：如图2，在四边形ABCD中，∠A=∠C，∠B=∠D.

求证：四边形ABCD是平行四边形.

师：这样，我们就得到了第三种判定方法，作为判定定理2：两组对角分别相等的四边形是平行四边形.

符号语言描述：因为∠A=∠C，∠B=∠D，所以四边形ABCD是平行四边形.

师：到目前为止，我们已经学了几种判定平行四边形的方法？

生8：三种.……

填表：性质判定平行四边形的对边平行；两组对边分别平行的四边形是平行四边形.平行四边形的对边相等；两组对边分别相等的四边形是平行四边形.平行四边形的对角相等；两组对角分别相等的四边形是平行四边形.平行四边形的对角线互相平分.我们再看生7提出的“对角线互相平分的四边形是平行四边形”.

命题：对角线互相平分的四边形是平行四边形.

已知：如图3，在四边形ABCD中，AC与BD相交于点O，OA=OC，OB=OD.

求证：四边形ABCD是平行四边形.

师：现在，我们得到了第四个判定方法，作为判定定理3：对角线互相平分的四边形是平行四边形.

符号语言描述：因为OA=OC，OB=OD，所以四边形ABCD是平行四边形.

填表：

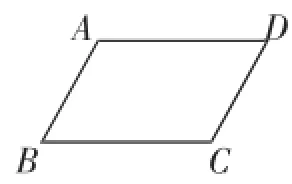
图2

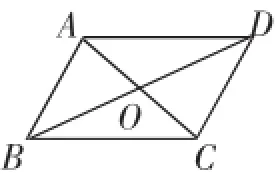
图3

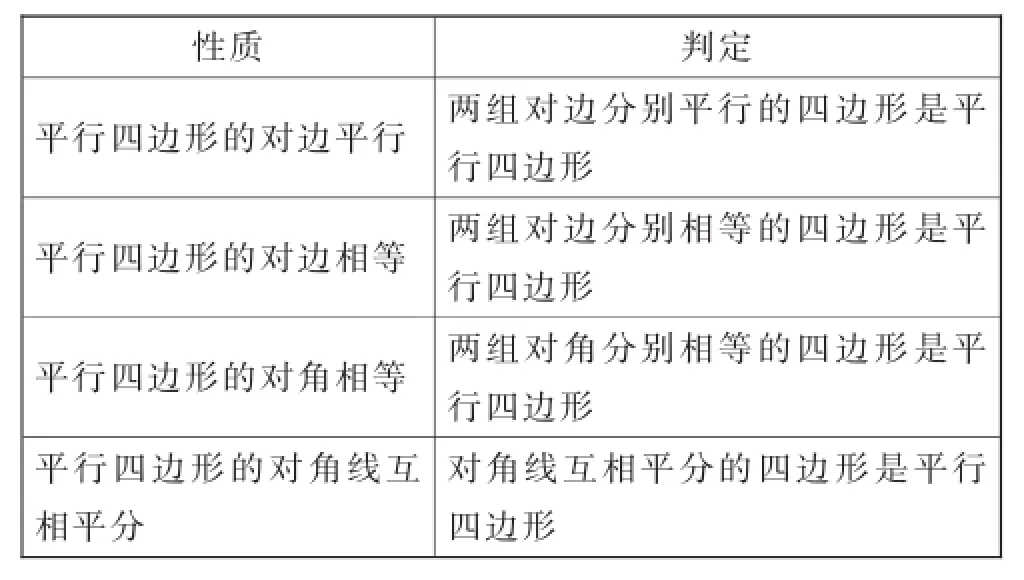
性质判定平行四边形的对边平行两组对边分别平行的四边形是平行四边形平行四边形的对边相等两组对边分别相等的四边形是平行四边形平行四边形的对角相等两组对角分别相等的四边形是平行四边形平行四边形的对角线互相平分对角线互相平分的四边形是平行四边形

师：现在，我们已经学会了4种方法来判定一个四边形是平行四边形.

从边：“两组对边分别平行”；“两组对边分别相等”.从角：“两组对角分别相等”.

从对角线：“对角线互相平分”，一共四种方法可以证明四边形是平行四边形.

（为了检验学生掌握的情况，给出一组练习）

练习1：判断下列四边形（图4～图6）是否为平行四边形？并说出你的依据.

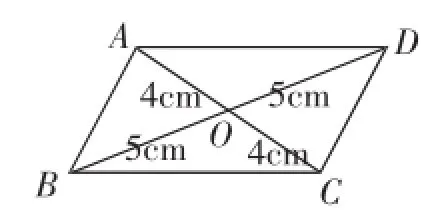
图4

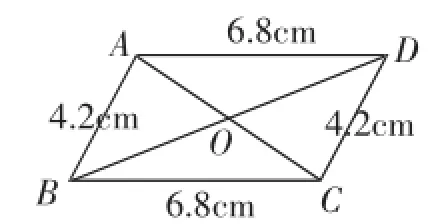
图5

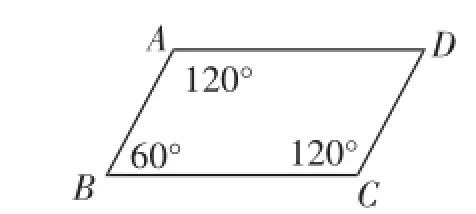
图6

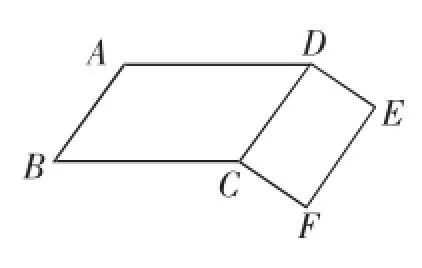
图7

练习2：如图7，AB=DC=EF，AD=BC，DE=CF，图中有哪些互相平行的线段？

3.例题讲评，跟进练习

例1如图8，平行四边形ABCD的对角线AC、BD相交于点O，E、F是AC上的两点，并且AE=CF.

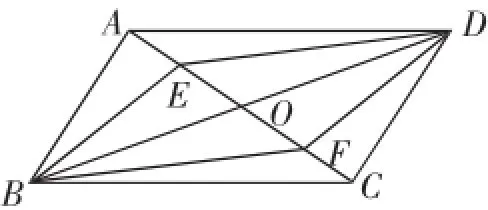
图8

求证：四边形BFDE是平行四边形.

预设互动：根据教学经验，不少学生都试图走全等三角形的证法证出两组对边分别相等或两组对边分别平行，这里还可以启发学生发现证明对角线互相平分的四边形是平行四边形.

跟进练习：如图9，在平行四边形ABCD中，已知AE、CF分别是∠DAB、∠BCD的角平分线，试说明四边形AFCE是平行四边形.

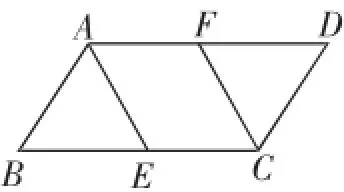
图9

预设点评：由于该题的证明路径不唯一，比如：①两组对角相等；②两组对边分别平行；③两组对边分别相等.在学生获得一种证明路径之后，鼓励其他学生分享自己的不同证法.

4.课堂小结，布置作业（略）

二、教后反思

上面简录了该课的教学实录，以下再从新知探究的方式和例题教学的对话视角给出两点反思.

1.“互逆命题”启发，生成新知，渗透研究套路

初中数学很多知识都具有互逆的特点，比如：代数中的运算（加与减、乘与除、乘方与开方）、整式乘法与因式分解等；几何中平行线的性质与判定、等腰三角形的性质与判定（“等边对等角”、“等角对等边”）、勾股定理与逆定理等，这些数学内容的研究经验启示学生在新学平行四边形的判定时，可以受到平行四边形性质的启发，将平行四边形性质中的条件与结论互换，研究它们的逆命题是否为真命题.正是基于互逆命题的启发下，我们在新知探究过程中，逐一逆向思考，探究出平行四边形的判定方法.更为重要的是，在这一探究过程中，学生知道了这些新的判定方法“源于何处”，也积累了数学研究的方法与经验.

2.追问不同证法，殊途同归，优化证明步骤

在上面课例中的例习题训练环节，我们没有满足于一例一解，习题简单核对答案式的习题讲评方式，而是在学生独立思考、贯通思路之后，追问有没有不同证法，让不同学生展示自己的思路，并追问这些思路对应着本课新学的哪一条判定方法，一方面，有效复习了新学内容，另一方面，也让更多学生看到其他学生的不同思路，感受证明思路的殊途同归.当然，教师起着必要的引导作用，在这里应该发挥“善于优化”（郑毓信教授语）的导向作用，即面对学生不同的证明方法，要引导学生本着“求简”思维，让自己的思路趋向更合理、更优化、更深刻的方向.

1.郑毓信.多元表征理论与概念教学［J］.小学数学教育，2011（10）.

2.李袆.高水平数学教学到底该教什么［J］.数学教育学报，2014（6）.

3.郑毓信.多元表征理论与概念教学（续）［J］.中学数学教学参考（上），2011（6）.

4.章建跃.构建逻辑连贯的学习过程使学生学会思考［J］.数学通报，2013（6）.H