藤蔓之美：让三个“一次”串珠成线——以一次函数复习课教学为例

☉江苏省江阴市利港中学于春波

藤蔓之美：让三个“一次”串珠成线——以一次函数复习课教学为例

☉江苏省江阴市利港中学于春波

受益于《数学通报》刊发李庾南老师关于“藤蔓之美”的函数起始课教学构思，笔者有机会执教一次函数复习课，专题复习三个“一次”（即一次函数与一元一次方程、二元一次方程组、一元一次不等式之间的关系），笔者从七年级的代数式出发，渐次生长，引导学生基于函数的视角看一元一次方程、一元一次不等式、二元一次方程组等知识，课堂上精彩生成不断，取得了较好的教学效果．本文梳理该课的教学设计，并附教后反思，提供研讨．

一、一次函数复习课教学流程

1.一路走来

复习七年级的相关概念，从代数式2x-1出发：

回顾1：多项式的概念：一次二项式.

回顾2：求代数式的值：当x=1时，……

回顾3：已知代数式的值为0，3，求未知数x的值；本质是解方程.

回顾4：若代数式的值大于5，求x的取值范围.

设计意图：通过一组七年级的列代数式、求代数式的值、已知代数式值逆向分析未知数的值，再进一步复习一次方程、不等式等学生熟悉的概念，为后续站在函数的制高点看待此前学过的概念而服务．

2.站在函数的高处观览

站在函数角度看上述问题，已知一次函数y=2x-1．

问题1：设y=2x-1，当x=1时，求函数值.

问题2：当y=0，3时，求自变量x的值.

问题3：当y＞3时，求自变量x的取值范围.

问题4：该函数的图像在x轴上方时，求x的取值范围；在同一平面直角坐标系中，再画出另一条直线y=-x+2．

问题5：两条直线与x轴交点距离是多少？它们与x轴交点的横坐标可看成哪两个方程的解？

问题6：两条直线有交点吗？如何求交点坐标？求交点的过程让你想起了哪个数学知识？

预设图像解读：如图1，两条直线交点P的坐标（1，1）对应着方程组的解．

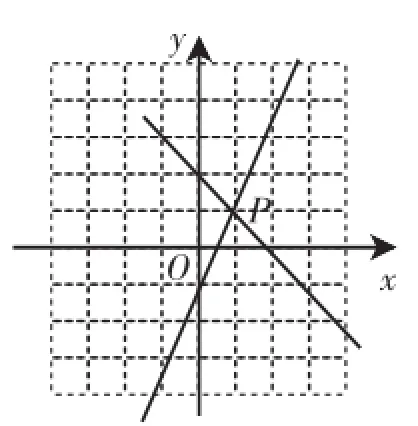
图1

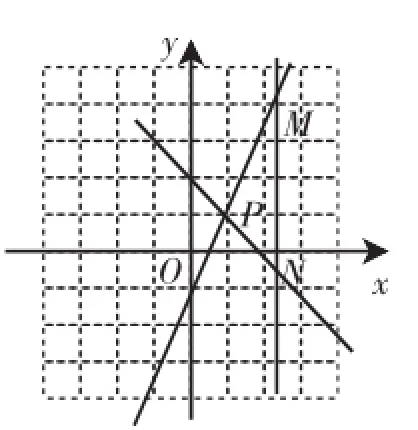
图2

问题7：当直线y=2x-1在直线y=-x+2上方时，对应的自变量x的范围是什么？

问题8：若直线x=a分别交上面两条直线于M、N两点，如图2，当MN=1时，求a的值．

预设讲评：设直线x=a与两条直线相交于M、N两点，用含a的式子表示M、N点的纵坐标，yM=2a-1，yN=-a+2，得MN=|（2a-1）-（-a+2）|=1．

讲评时使用PPT的动画功能渐次呈现，截图如图3所示.

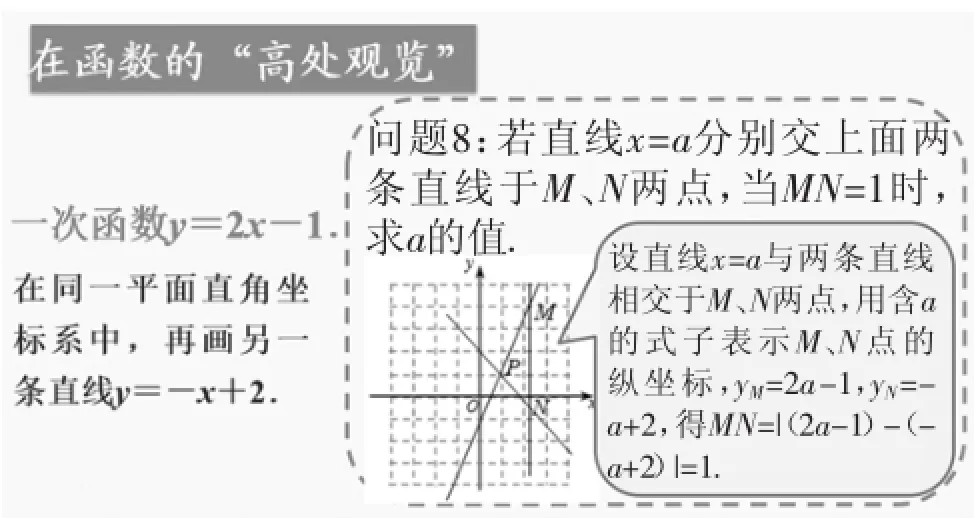
图3

设计意图：将此前复习的代数式的值、方程、不等式问题，用函数的背景包装起来，本质上它们仍然是一样的，引导学生从函数的角度看待问题、解决问题．

3.它们是一样的吗

题2：在同一平面直角坐标系xOy中，直线y=2x-1与直线y=-x+m相交于点A（1，1），求m的值.

第二组：

题4：在同一平面直角坐标系xOy中，若三条直线y= 2x-1，y=-x+m，y=x相交于一点，求m的值.

第三组：

题5：在同一平面直角坐标系xOy中，若两条直线y= 2x-1，y=-x+m的交点在第一象限，求m的取值范围.

设计意图：通过三个不同的题组，对比含有参数的一次函数与方程（或不等式）之间的关系.加深理解函数问题与此前练习过的一些题型之间的和谐与一致，即感受到“它们是一样的”.

第四组：

题7：在同一平面直角坐标系xOy中，若一次函数y= -2x-4与y=4x+b的图像交点在第三象限，则b的取值范围是（）.

A.-4＜b＜8 B.-4＜b＜0

C.b＜-4或b＞8 D.-4≤b≤8

预设以下两种角度的解法讲评：

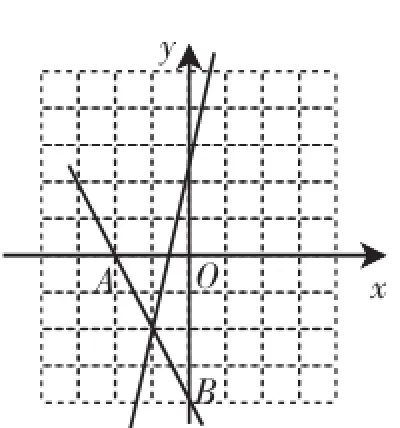
图4

“形”的解法：先画出直线y=-2x-4，设交x轴，y轴于A，B点，如图4，再画出符合要求的一条直线y=4x+b，考虑两处极端位置，即当直线y=4x+b分别经过A，B点时，可求出b=8或-4，即-4＜b＜8.

A.-4＜b＜8 B.-4＜b＜0

C.b＜-4或b＞8 D.-4≤b≤8

设计意图：在详细讨论题7的不同解法之后，出示题8的目的是让学生感受不同形式问题在解法上的一致，进一步感受函数视角下的方程与不等式问题，同时也传递解法过程中数形结合的优越性.

4.藤蔓之美

小结阶段，PPT呈现藤蔓图片（图5），引导学生从函数的视角谈谈对此前所学的方程、不等式、方程组的理解.

图5

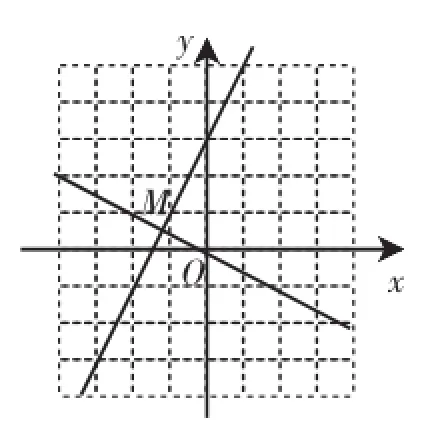
图6

5.布置作业

（1）如图6，在同一平面直角坐标系xOy中，一次函数y=-x与y=2x+3的图像交于点M.

①求出点M的坐标；

③当直线y=2x+3在x轴下方时，求自变量x的取值范围；

（2）一次函数y=kx+3与y=3x+6的图像的交点在x轴上，求k的值.

（3）已知直线y1=2x-7和y2=-3x+8，当x＞3时，y1＞y2；当x＜3时，y1＜y2，求直线y1=2x-7与y2=-3x+8的交点坐标.

（4）已知关于x，y的二元一次方程3mx+2ny=0和5mx-3ny=19转化成的两个一次函数的图像的交点坐标为（1，-1），求m，n的值.

二、教后反思

1.复习课的选题宜简单出发，渐次生长，拓展深化

就我们观摩的不少复习课研讨活动中，所选例题往往偏难，以为选编了一些所谓的中考题、综合题就是复习课的需要.其实，复习课首先要重视的是基础，为学生梳理此前所学的基础内容、核心内容是否全部掌握，如果掌握的情况不好，则还需要训练、讲评，让更多的学生掌握应知必会的数学概念或性质.在此基础上，可以将例题或习题渐次生长、拓展深化，让高层次学生通过复习课的学习，知道较难问题的源头活水，难题解法思路是如何自然生成的.

2.复习课的选题宜重视关联，前后呼应，促进内化

复习课的选题需要兼顾不同教学环节下的关联，如上面课例中的开课环节，看似复习七年级的代数式的相关概念和求值问题，但对应着下一教学环节中的函数问题，让学生内化理解这些问题在本质上都是一致的.特别是，在教学环节“它们都是一样的吗”中，我们预设一些题组，看似考查不同领域的数学知识，然而它们的求解却高度类似，通过这样的比较，让学生感悟出数学命题的“多元表征”，需要他们练就一双“火眼金睛”，切实提升学生的解题能力.

3.复习课的讲评宜展示交流，对话追问，促进理解

由于预设的很多例题及变式都充满关联，前后呼应，所以在学生独立贯通思路之后，要安排学生展示交流，教师与学生之间通过对话和追问，让更多学生的思维参与进来，促进理解.对于一些较难问题的思路，可以安排学生上台对照课件演示讲解，然后追问其他学生的理解，通过“请你再说一遍”来促进更多学生积极思维、参与课堂.

1.李庾南，刘东升．藤蔓之美：从数式方程走向变量函数——以八年级“函数”第1课时教学为例［J］．数学通报，2015（2）.

2.钟启泉．新旧教学的分水岭［J］．基础教育课程（上），2014（2）.

3.李庾南．自学·议论·引导教学论［M］．北京：人民教育出版社，2013．H