学生课堂追问引发的思考

●孙小龙

(如皋市第一中学 江苏如皋 226500)



学生课堂追问引发的思考

●孙小龙

(如皋市第一中学 江苏如皋 226500)

笔者在讲解一道直线与圆位置关系试题时，有学生质疑解题过程中的设法，笔者随即与学生进行了交流，随着学生的逐步追问，师生对疑虑进行了深入地探究.

题目 求经过直线2x-y+3=0与圆x2+y2+2x-4y+1=0的交点，且面积最小的圆的方程.

解 设圆的方程为

x2+y2+2x-4y+1+λ(2x-y+3)=0(其中λ∈R)，即

x2+y2+(2+2λ)x-(4+λ)y+1+3λ=0.

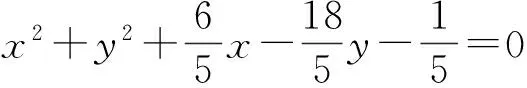
该解法设法巧妙，圆随着λ的变化而运动，利用函数思想快速求出了面积最小的圆的方程.

一位喜好钻研的学生问：为什么这样设？为什么这样设的曲线一定表示经过直线和已知圆交点的圆呢？

(对于学生提出的这个问题，笔者胸有成竹.)

师：对于方程x2+y2+2x-4y+1+λ(2x-y+3)=0(其中λ∈R)，方程组

的解一定满足曲线方程，即经过已知直线与圆的交点.

学生追问：为什么这样设的曲线方程一定表示圆呢？

师：因为这是一个二元二次方程，而且满足圆的一般方程的特点，所以表示圆.

学生又追问：圆的一般方程表示圆除了形式上的特点，还有一个重要的条件是：

D2+E2-4F>0，

你没有验证怎能直接说该曲线表示的是圆呢？

学生的提问有理有据，没有任何破绽，笔者感到很欣慰，表扬学生很细心，有质疑精神.

师：方程整理可得

x2+y2+(2+2λ)x-(4+λ)y+1+3λ=0，

D2+E2-4F= (2+2λ)2+(4+λ)2-4(1+3λ)=

5λ2+4λ+16,

由5>0，Δ<0,可得5λ2+4λ+16>0恒成立，方程表示的曲线一定表示圆.

师：当D2+E2-4F≤0时，方程表示一个点或者不表示任何曲线，而直线2x-y+3=0与圆x2+y2-2x-4y+1=0相交，有2个不同的交点，方程x2+y2+2x-4y+1+λ(2x-y+3)=0(其中λ∈R)一定经过2个不同的点，于是D2+E2-4F>0成立，曲线方程一定表示圆.

学生再次追问：方程x2+y2+2x-4y+1+λ(2x-y+3)=0(其中λ∈R)表示经过直线2x-y+3=0与圆x2+y2+2x-4y+1=0的交点的圆，能表示经过交点的所有圆吗？

此时笔者一愣，这个问题确实没有考虑到，而且应该思考.前面设直线方程时，要求学生分斜率存在与不存在这2种情况考虑，其实就是希望学生不要漏了斜率不存在的直线，造成失解.学生的追问不也是要说明这个问题吗？在赞赏学生思维缜密的同时，如何解决这个问题？师生展开了进一步地探讨，彻底解决了这个问题.

设直线2x-y+3=0与圆x2+y2+2x-4y+1=0的交点为A(x1,y1),B(x2,y2),设经过点A,B的圆的方程为

x2+y2+Dx+Ey+F=0(其中D2+E2-4F>0),

则

2个式子相减可得

(D-2)x1+(E+4)y1+F-1=0,

同理可得 (D-2)x2+(E+4)y2+F-1=0，

可得点A(x1,y1),B(x2,y2)在直线

(D-2)x+(E+4)y+F-1=0

上.因为经过点A,B的直线只有1条，所以方程(D-2)x+(E+4)y+F-1=0和2x-y+3=0表示同一条直线，对应的系数应成比例，不妨设

(D-2)x+(E+4)y+F-1=λ(2x-y+3)，

可得Dx+Ey+F=λ(2x-y+3)+2x-4y+1，

此时方程x2+y2+Dx+Ey+F=0可化为

x2+y2+2x-4y+1+λ(2x-y+3)=0(其中λ∈R).

仔细分析上述探究，发现可利用2个圆的相交弦方程进行推导：由圆x2+y2+2x-4y+1=0及经过点A,B的圆的方程

x2+y2+Dx+Ey+F=0(其中D2+E2-4F>0),

相减可得直线AB的方程为

(D-2)x+(E+4)y+F-1=0，

其余同上.

经上述论证，经过点A,B的圆与方程x2+y2+2x-4y+1+λ(2x-y+3)=0(其中λ∈R)表示的圆是等价的.

教学反思 1)培养学生的质疑精神.现代教育体制下，大部分学生没有质疑精神，很少质疑教师传授的知识.少部分学生在质疑时，对教师的解答有时似懂非懂，却不敢追问，仍然稀里糊涂.为了培养学生的质疑精神，教师要营造有利于学生主动质疑的良好氛围，鼓励学生大胆质疑;欢迎他们与自己争论，对学生的质疑给予充分肯定，特别是对平时课堂上敢于发表反驳意见的学生，更要予以表扬;即使他们的观点是错误的，也要在肯定学生勇于质疑的前提下，与学生一起讨论来加以引导，并纠正学生的错误观点，从而保护学生质疑的热情，树立学生质疑的信心.教师还要鼓励学生敢于质疑教师、质疑课本、质疑权威，“金无足赤，人无完人”,教师不是圣人，在课堂上，教师也会出现问题，鼓励学生大胆质疑，善于思考，点燃学生自主学习的激情.

2)教学相长.教学是教与学的交往互动，师生双方相互交流、相互沟通、相互启发、相互补充，在这个过程中教师与学生进行情感交流，从而达到共识、共享、共进，实现教学相长与共同发展.教和学互相影响和促进，共同得到提高.通过学生的追问弄清了经过点A,B的圆与方程x2+y2+2x-4y+1+λ(2x-y+3)(其中λ∈R)表示的圆是等价的.在解除学生顾虑的同时，教师也实现了自我的提高与认识的升华.就这一点来说，教师也应该培养学生的质疑精神.

3)积极反思，完善自我.教师的教学容易受到既有经验的影响，循规蹈矩，对一些公认、权威处于默认、服从的状态.而对于学生而言，这些是全新的，学生会在学习中理解，在理解中质疑，在鼓励学生质疑的同时，教师更应该在教学中积极反思，面对权威，要敢于质疑，不应一味顺从.上述学生的追问理由充分，但课后笔者向同组教师了解时，大多数教师却表示未能思考到.教师在讲解时，多次强调化简、设直线等要注意等价性，而自己在面对时却口是心非，怎能让学生信服呢？笔者用质疑的眼光梳理了一下，发现在教材、典型试题中也存在类似的问题，有待更正与商榷.

(a2-cx)2=a2[(x-c)2+y2],

即

(a2-c2)x2+a2y2=a2(a2-c2).

令a2-c2=b2(其中b>0)，可得椭圆标准方程为

(a2-cx)2=a2[(x-c)2+y2]，

等价吗？从式子的化简角度看是不等价的.教材对此未作说明，也未在椭圆几何性质一节中补充说明，这容易对学生产生误导.笔者认为教学时应该弥补.具体如下：

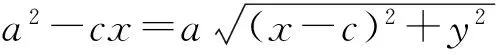
即

即

亦即

例1 已知数列{an}的前n项和为Sn，a1=1，满足下列条件：

①对任意n∈N*，an≠0,

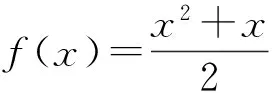
1)求数列{an}的通项an及前n项和Sn；

2)求证：0≤|Pn+1Pn+2|-|PnPn+1|<1.

1)解 由题意可得

当n≥2时,

整理可得 (an+an-1)(an-an-1-1)=0.

又因为对任意n∈N*，an≠0，所以

an+an-1=0或an-an-1-1=0.

当an+an-1=0时，

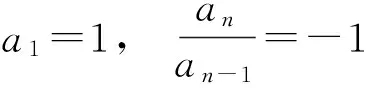
得

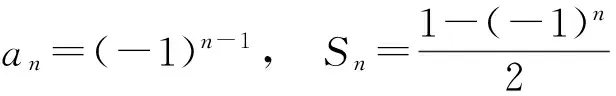
当an-an-1-1=0时，

a1=1，an-an-1=1，

得

2)证明 当an+an-1=0时，

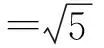
从而

|Pn+1Pn+2|-|PnPn+1|=0.

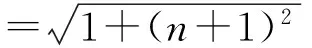
于是 |Pn+1Pn+2|-|PnPn+1|=

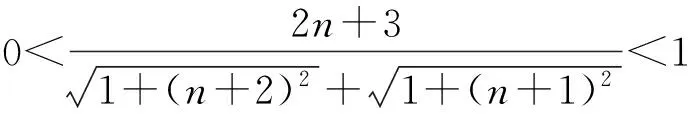
综上可得0≤|Pn+1Pn+2|-|PnPn+1|<1.

此题在综合试卷中出现频率较高，上述为各综合试卷和百度搜索中提供的参考答案，看上去思路清晰，逻辑性强，是大家公认的标准答案.

第1)小题中的2种结果在证明第2)小题时恰到好处地与结论进行了衔接，似乎没有任何问题.但笔者经过研究之后发现此题和参考答案均存在问题，不妨从数列{an}的前3项说起：

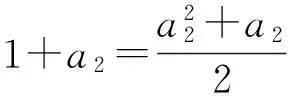
解得

a2=-1或a2=2.

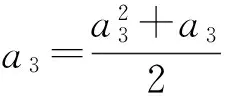
解得

a3=1.

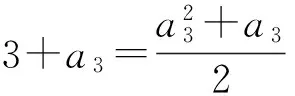
解得

a3=3或a3=-2.

综上所述：a1,a2,a3共有3种可能，分别为1,-1,1；1,2,3；1,2,-2.

而从上述参考答案得到的a1,a2,a3却只有2种可能，分别为1,-1,1；1,2,3.出现矛盾，究竟谁是谁非？

同理再算一算a4.当a3=1时,a4=-1或a4=2；当a3=-2时,a4=-1或a4=2；当a3=3时,a4=4或a4=-3.a4有6种可能，从而a1,a2,a3,a4共有6种可能，而从上述参考答案得到的a1,a2,a3,a4同样只有2种可能.显而易见，上述参考答案是错误的.

此题中突出的是正项数列，本题中则为任意n∈N*，an≠0，难道正是因为这个条件的变化导致了本题的错误吗？运用这个条件的是等式

(an+an-1)(an-an-1-1)=0.

若{an}为正项数列,则an+an-1>0,即an-an-1=1，则数列{an}为等差数列，可得an=n.

若对任意n∈N*，an≠0，则

an+an-1=0或an-an-1-1=0，

参考答案由此得到了数列{an}为等比数列或等差数列，实质理解为an+an-1=0对n≥2恒成立或an-an-1-1=0对n≥2恒成立，但是由an+an-1=0或an-an-1-1=0只能说明对于一个确定的n(其中n≥2)必有一个成立，但不一定是其中的一个恒成立，可以是对一部分n(其中n≥2),an+an-1=0成立，而对另一部分n(其中n≥2),an-an-1-1=0成立，显然参考答案的理解是其中一种非常特殊的情况，有失偏颇.

从上面的分析可知本题的第1)小题情况非常多，无从回答，第2)小题更无从谈起.一道出现频率较高的试题竟然是一道错题，着实让人惊讶！

在平时的教学过程中教师应做好学生的表率，不迷信经典，不迷信权威，不全盘吸收，勇于质疑，勇于挑战，大胆纠错，在不断的质疑中提高自身的数学素养.