数学变换在解题中的应用与启示

(西宁市第二中学 青海西宁 810012)



数学变换在解题中的应用与启示

● 赵小卫

(西宁市第二中学 青海西宁 810012)

在数学里，变换是一个基本概念.例如，平面几何里常见的合同变换、相似变换还有等积变换，在解析几何里常用到的坐标变换，线性代数当中的线性变换,仿射几何里的仿射变换等等.所有这些变换,说到底就是一种映射，其中用变换群来研究对应几何学的观点，最早是由德国数学家克莱因提出来的，其意义在于把当时已有的几何统一在变换群的观点之下，继而突出了变换群在几何中的地位.按照这一背景，在实施数学教学的过程中，通过数学变换的应用与研究有助于我们厘清各种数学对象或者2个数学集合间的内在关系，这样在认识数学的本质同时也有利于获得一些重要的数学思想方法.虽然数学变换早已在初中、高中阶段得到了广泛的应用，但对数学变换本身的地位、作用以及不同变换的关系说明得不够明确，更缺乏系统性，因此适度加强数学变换的教育意识有助于我们了解更多有关数学的本质特征.下面笔者借《数学通报》2013年第8期中的2 137号征解题作为线索谈一谈数学变换的思想作用，请大家予以赐教.

问题 在△ABC中，分别过点A,B作它的外接圆的切线相交于点P，联结PC交圆于点D，交AB于点E，求证:

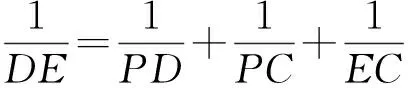
代数不过是书写的几何，而几何不过是图形的代数——索菲娅·格梅茵.由此出发可以先作图与式的变换：

图1

证法1 如图1，分别以直线PO,AB为x轴、y轴建立平面直角坐标系.设P(a，0)，直线PC的倾角为α，则直线PC的参数方程为：

另设圆心为O′(k，0)，⊙O′的半径为r,则⊙O′的方程为

(x-k)2+y2=r2.

将直线PC的参数方程代入圆方程得

(a+tcosα)2-2k(a+tcosα)+k2+t2sin2α=r2,

化简得

t2+2(a-k)tcosα+(k-a)2-r2=0,

于是

t1+t2=-2(a-k)cosα,

t1t2=(k-a)2-r2,

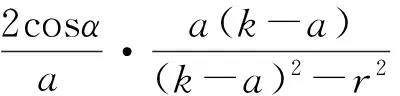
又在Rt△PAO′中，根据勾股定理得

PA2=O′P2-O′A2=(k-a)2-r2,

按照射影定理可得

PA2=PO·PO′=|a|(k-a),

故

从而

即

得

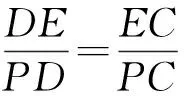
亦即

PD·EC=DE·PC，

故

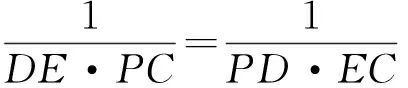
因此

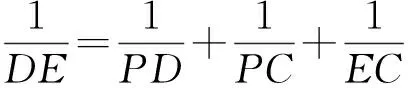
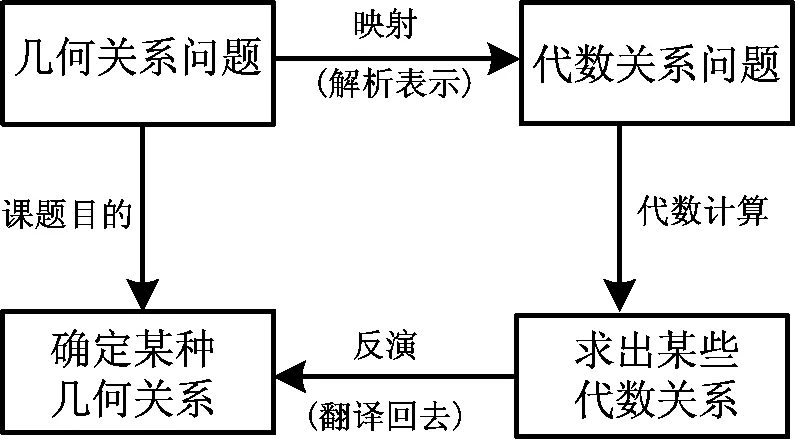
图2

证法2 以点P为极点、射线PO为极轴建立极坐标系.设O′(m,0)，⊙O′的半径为r，射线PC的方程为θ=φ，∠PO′A=β,则AB的方程为

ρcosθ=m-r·cosβ,

于是

故

又⊙O′的方程为

ρ2-2ρm·cosθ+m2-r2=0,

因此

即

从而

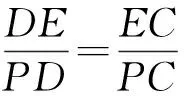
亦即

PD·EC=DE·PC,

故

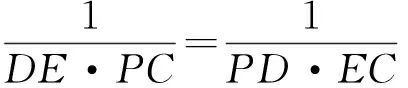
因此

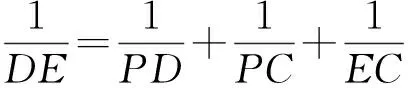
评注 证法2实际上是依据直角坐标与极坐标间的对应关系，把证法1中直角坐标形式下的坐标和方程分别转变成了极坐标形式下的坐标和方程，并通过这一形式上的变换得到了用极坐标同样可解的方法.它体现的是一种以对应为基础的数学变换关系——坐标变换.这里2个坐标系间的坐标变换关系为：x=a+ρ·cosθ,y=ρ·sinθ,k=m+a.

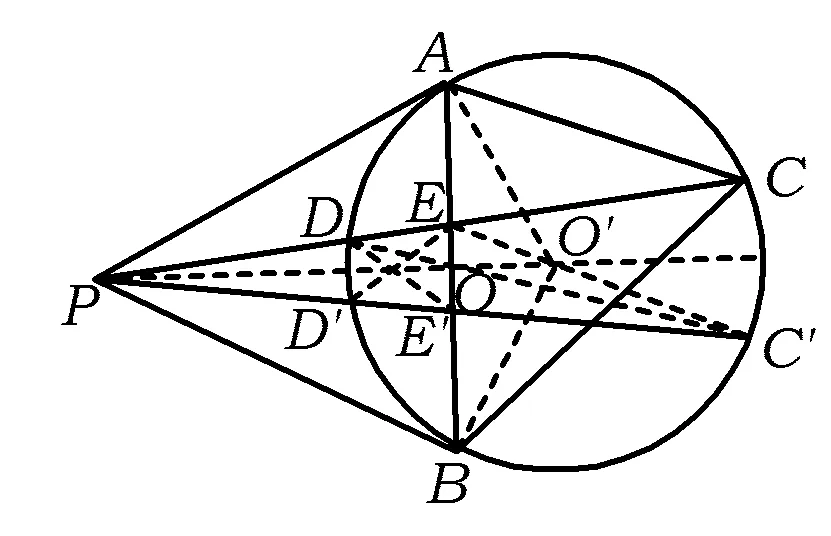
图3

证法3 如图3，作PC关于PO′的对称图形PC′,交⊙O′于点D′,C′,交AB于点E′,联结D′E,EC′,DE′,DC′，则

PC·PE+PD·PE=

PE·PC′+PD·PE′,

PC·PD=PD·PC′,

故

因此

即

亦即

PD·EC=DE·PC,

故

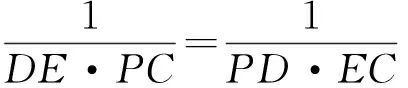
因此

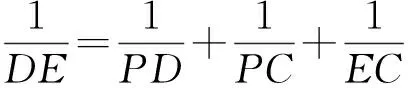
评注 证法3是把在同一直线上的4条线段PD,PC,EC和DE利用平面几何中的轴对称变换分散到2条直线上，然后再利用面积法对问题给予证明的方法.这里所采用的轴对称变换实际上是合同变换中的一种，所谓合同变换亦称全等变换或正交变换，其形状和大小完全相同的图形就叫合同形，合同变换主要含平移变换、旋转变换以及轴对称变换.

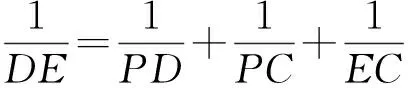
凡此种种，引发我们的思考：究竟什么才是数学的本质？数学解题除了逻辑以外的部分又是什么？所有的这些问题或许只有透过各种不同的数学变换才能让人们找到数学的神韵和真谛.实际教学中又该怎样通过数学变换把各部分内容有机地整合在一起，还需要进一步实践和探索.