万变考题 课本寻根——谈一道平面向量题的改编

●耿道永

(苏州工业园区第二高级中学 江苏苏州 215121)



万变考题 课本寻根
——谈一道平面向量题的改编

●耿道永

(苏州工业园区第二高级中学 江苏苏州 215121)

平面向量在高考试题中多以中档题形式出现，这类试题一般区分度较好，能有效考查学生的基础知识和基本能力.由于这部分内容看起来比较“抽象”，因此很多学生感觉做这类题比较“吃力”.下面通过研究平面向量中常考的一道题根，以期帮助学生掌握这类题的解题策略.

1 原题及解法

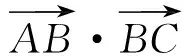
(苏教版教材《数学(必修)》第499页第12题)

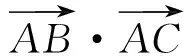
解法1 由题设可知∠A=90°，故

解法2 如图1，以AC为x轴、AB为y轴建立直角坐标系.易知B(3，0),C(0，4)，从而

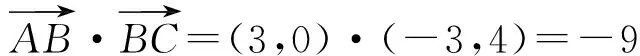
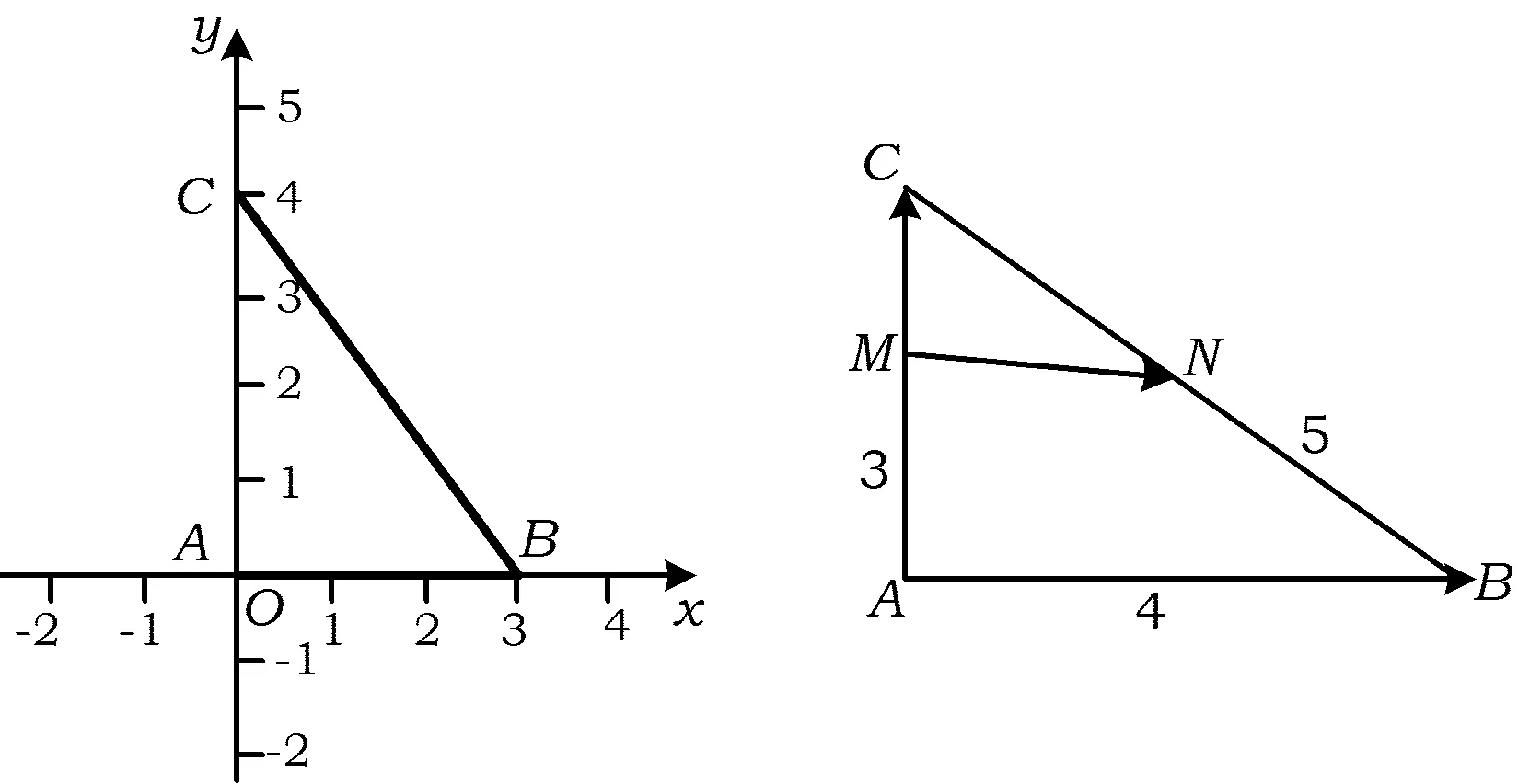
图1 图2

评注 向量是高中阶段数形结合的完美典范，在解题中尽可能地引导学生从代数和几何这2个角度审视和考查向量问题.“数”一般指向量的坐标方法，“形”一般指向量的基底方法.

2 6个层次的改编

改编层次1 改变三角形形状

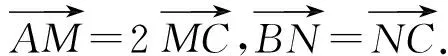
(2015年北京市数学高考理科试题)

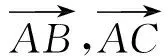
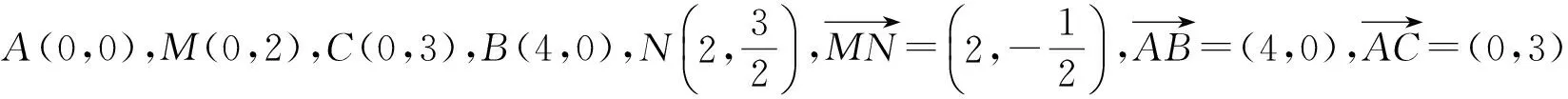
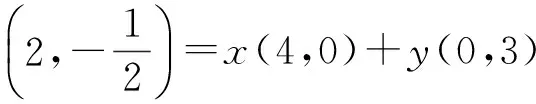
即

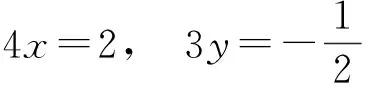
解得

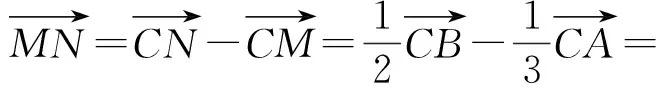
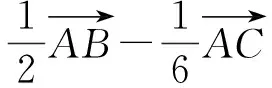
得

评注 对于一些非直角三角形，一般借助于基底法来解决，作为客观题，特殊化也是一种有效的策略.当然，对于等腰三角形，也可以利用“三线合一”的性质建立坐标系.

改编层次2 和其他数学知识综合

( )

A．13 B．15 C．19 D．21

(2015年福建省数学高考理科试题)

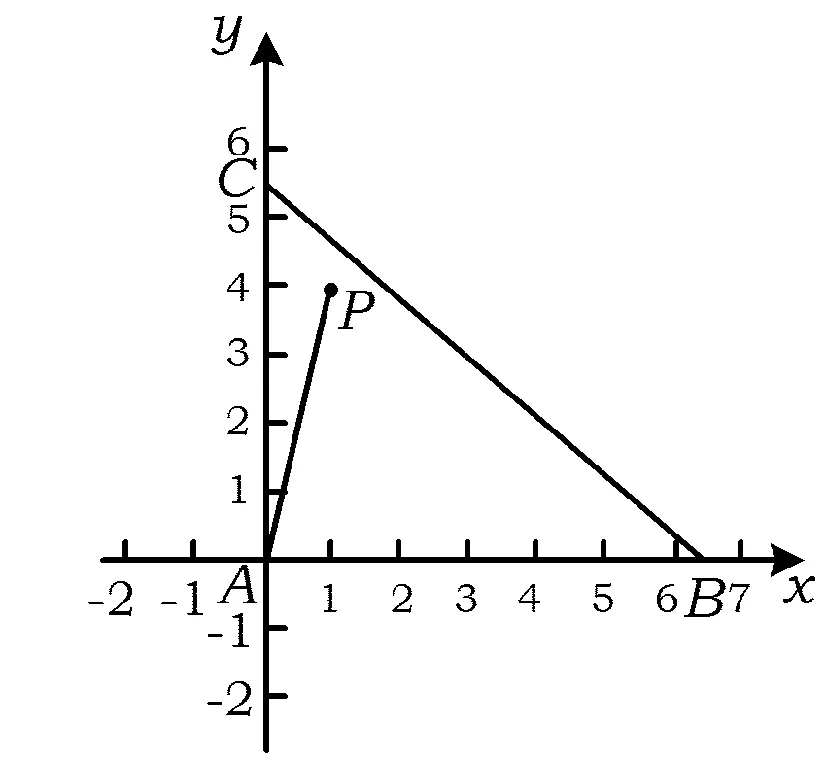
图3

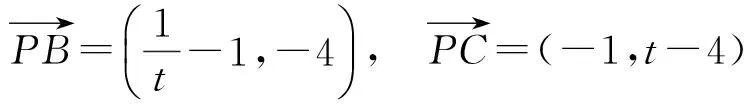
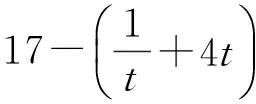
下同解法1.

评注 本题和基本不等式知识相结合，体现了小题综合化的趋势，属于区分度较好的一道题.

改编层次3 以矩形为背景

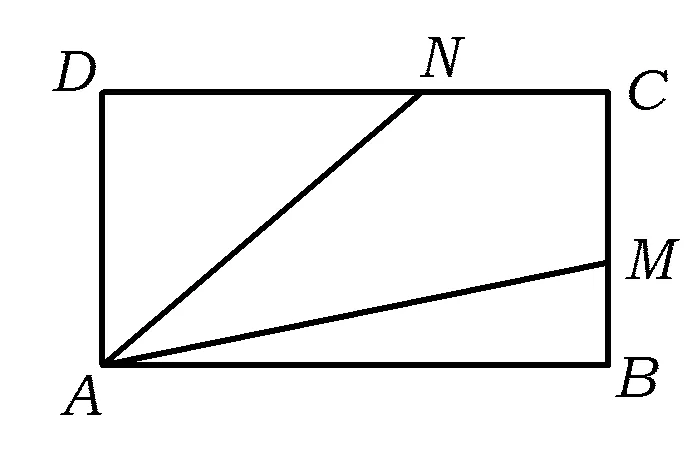
图4

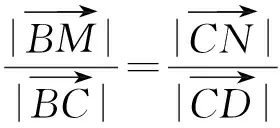
(2012年上海市数学高考文科试题)

分析 本题的难点是2个比例相等该如何运用，可以引进一个中间量来处理.

.

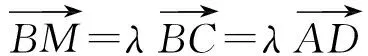
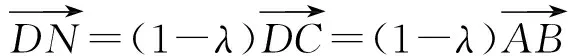
又因为0≤λ≤1，所以

解法2 分别以AB,AD所在的直线为x,y轴建立直角坐标系.由

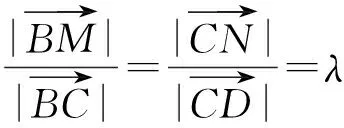
得BM=λ，CN=2，从而M(2，λ)，N(2-2λ，1)，于是

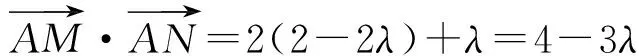
下同解法1.

评注 建系后把向量运算转化为代数运算，达到“化抽象为具体、化陌生为熟悉”的目的，一般出现直角的图形建议建系处理.

改编层次4 以平行四边形(菱形)为背景

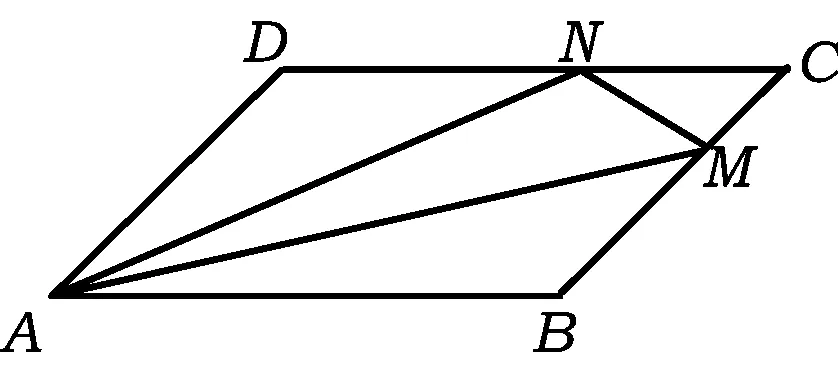
图5

( )

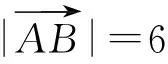
A.20 B.15 C.9 D.6

(2015年四川省数学高考理科试题)

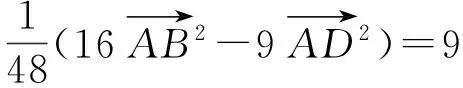
故选C.

解法2 假设AB⊥AD，以AB为x轴、AD为y轴建立直角坐标系.易知M(6，3),N(4，4),从而

故选C.

评注 特殊化建系解决客观题还是蛮容易的.

( )

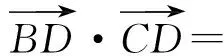
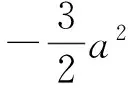
(2015年山东省数学高考理科试题)

解法1 由菱形ABCD的边长为a，∠ABC=60°可知

∠BAD=180°-60°=120°,

故选D.

图6

解法2 如图6建立直角坐标系，则

B(a,0),

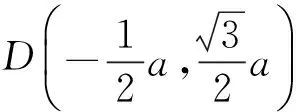
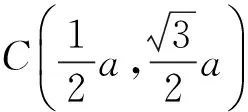
评注 本题虽然不是矩形，但是角度也比较特殊，因此建系和基底法平分秋色.

改编层次5 以梯形为背景

(2015年天津市数学高考理科试题)

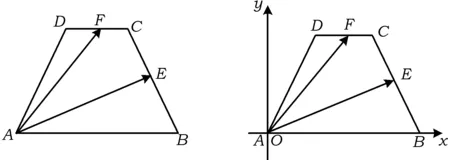
图7 图8

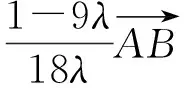
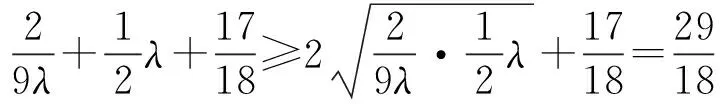
解法2 如图8建立直角坐标系，由题设及平面几何知识易求得

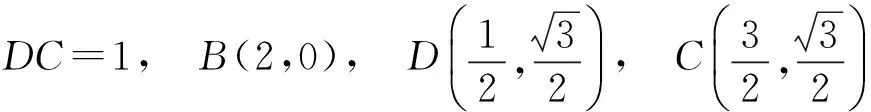
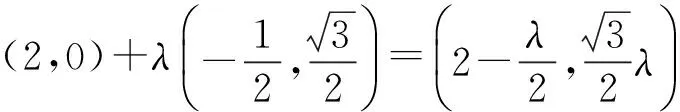
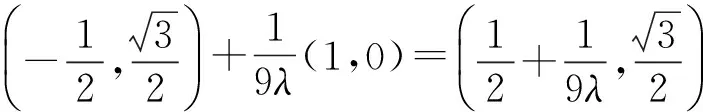
下同解法1.

评注 本题背景、参数、融合的知识(不等式)都变得复杂了，基本是前面所有题型的综合.

改编层次6 以组合图形为背景

分析 注意到正三角形“三线合一”，因此可以考虑建系处理，也可以采用基底法处理.

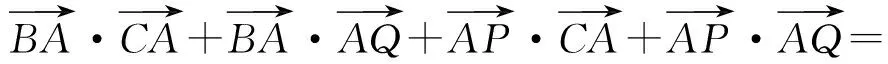
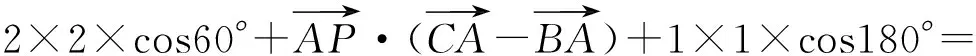
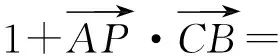
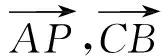
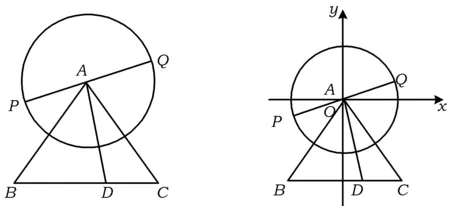
图9 图10

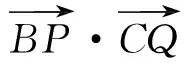
评注 对于组合图形建系解决问题时，坐标系的选择很重要，建系的原则之一是涉及到的点的坐标比较简单.

以上题型把向量的数量积的2种形式、向量的加减法有机结合，涵盖了向量的主干内容，并且方法灵活，容易与其他知识综合，作为考试的重点和热点也就不足为奇了.