一道高考模拟题的教学实录及反思*

●何洪标 蓝云波 黄伟宽

(兴宁市第一中学 广东兴宁 514500)



一道高考模拟题的教学实录及反思*

●何洪标 蓝云波 黄伟宽

(兴宁市第一中学 广东兴宁 514500)

习题课是数学教学的一种常见课型，特别是高三的课堂教学，习题教学几乎贯穿整个高三复习的始终.我们经常会看见这样一种情景：一大群莘莘学子忙忙碌碌，整日游弋在题海中，做的题集铺天盖地，但效果却并不见佳.究其原因，他们只是在模仿、记忆做题，并不会思考和分析问题，对一些重要的知识点和解题思想缺少经历和内化的过程；对他们而言，解题仅仅是简单的操作层面的机械模仿.因此，习题教学的高效性显得尤其重要.笔者结合高三复习课“导数在研究函数中的应用”的教学设计，谈谈习题教学的有效性并提供一些方法，供同行参考.

1 教学实录

1)求a的值；

2)若对任意x∈[1,+∞)，f(x)≤m(x-1)恒成立，求m的取值范围；

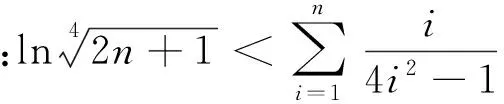
(2013年山东省济南市二模理科数学试题)

上课之前，笔者把该题作为作业布置给学生，让学生认真探究、分析及解答，并要求及时上交.通过批改作业，笔者获悉了学生答题的详实情况，并掌握了大量的教学素材,为课题教学的顺利进行奠定了基础.

1.1 关爱差生，共同参与

师：同学们，这是之前布置的一道习题(多媒体投影出该题).从批改情况来看：绝大部分同学都能做对第1)小题，不少同学能做对第2)小题，只有少数同学能完成第3)小题.下面让我们一起进入此题的探索之旅.先请生1说说，你对此题的第1)小题是怎么思考的？

(由于第1)小题较为简单，笔者提问了一位基础较为薄弱的学生.)

生1(并不自信，回答起来有点慌张)：先求导函数，结合切线与直线2x+y+1=0垂直，然后利用导数的几何意义求解(说完有点不好意思).

教师及时投影出生1的解答过程：因为

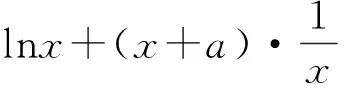
所以

f′(1)=1+a,

师：生1的思路清晰，其他同学都认同上述解法吗？

(此时，笔者观察到好几个学生跃跃欲试，但笔者提问了其中一位同样基础不是很好但做对了此题的生2.)

师：生2的解答非常漂亮！生1的思路是正确的，同样值得肯定！可惜生1求导法则用错了，细节没有处理好，这是我们需要警惕的.一旦前面出错了，后面洋洋洒洒的解答也就变得毫无意义了.

1.2 发散思维，共同探究

美国著名的心理学家吉尔福认为:创新性思维具有流畅性、变通性和独创性的特点.而发散思维是培养学生创新思维的重要手段.在教学中应鼓励学生从不同角度出发，得出不同的解法.

师：请生3说说你对第2)小题的看法.

师：生3遇到的解题瓶颈也是不少同学的共同问题，不过思路是自然的，能不能改进呢？或者有无其他的思路呢？

师：做不下去的原因是什么呢？

学生(齐声)：导函数越求越复杂.

师：大家都发现了这个问题，这是我们利用导数研究函数问题中常遇到的一个比较棘手的问题.既然如此，能不能通过等价转化，让导函数越求越简单呢？

生5：可以把lnx分离出来，再构造函数.

教师投影出生5的解答过程：由第1)小题知

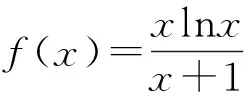
对任意x∈(1,+∞)，要使f(x)≤m(x-1)成立，即

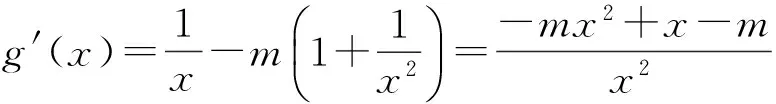
①若m≤0，g′(x)>0,g(x)≥g(1)=0,这与题设g(x)≤0矛盾.

师：太漂亮了！生5的解答有效地解决了导函数越求越复杂的问题.导函数原先之所以越求越复杂，是因为lnx与其他式子结合在一起，而生5把lnx分离出来之后再构造函数，达到了我们所希望的效果.太棒了！为了区别于分离参数法，我们能不能给这种技巧一个适合的名字呢？

学生(几乎是齐声)：分离函数.

师：太贴切了，我们有分离参数的技巧，现在又有一种分离函数的技巧了，太棒了！以后我们在解答含有lnx或ex的函数问题，遇到导函数越求越复杂时，不妨考虑使用这种技巧.还有其他不同的见解吗？

生6：受此启发，我发现生3的思路可以继续做下去.

师：请继续分析……

此言一出，众生立即兴奋起来，奋笔疾书.笔者发现生7的解答不错，距离答案仅一步之遥，这正是笔者所希望看到的.教师投影出生7的解答过程：

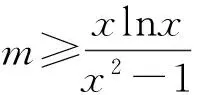
设h(x)=-x2lnx-lnx+x2-1，则

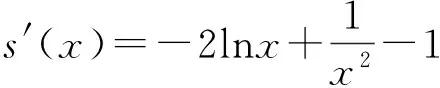
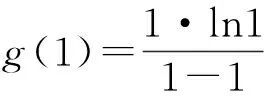
师：现在请生7分析一下你的解题思路.

生7：求出g′(x)之后，我发现整个式子比较复杂，联想到刚才老师所说的“局部求导”，故我想到只需确定分子的符号即可，于是进行“局部求导”，但“局部求导”之后，还是比较复杂，但与原来的式子相比较简单了一些，于是进行了多次求导.我发现整个推理过程无误，但不知为何做不出答案，因为g(1)无意义.还请老师明示.

师：非常有想象力，太棒了！你的思路没问题，很多高考题都是多次求导解答的，只不过适合此解法的高考题中，端点值是有意义且能求得出的，而这道题中的g(1)是无意义的，因为分母为0.但它的极限值却是存在的，解答这个问题，需要用到高等数学中的洛必达法则.我们了解下即可，有兴趣的同学课后可与老师交流.

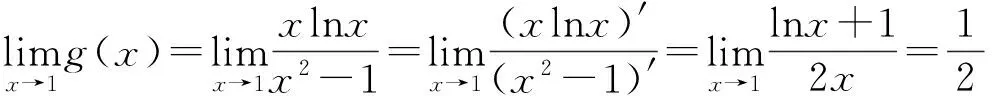
师：这样，我们通过第2)小题的分析和探究，得到了解决有关函数问题的重要思想与技巧：分离参数、分离函数、局部求导、多次求导.希望同学们用心体会，并吃透其中的思想方法.正所谓：题不在多，经典则灵！

此时，笔者往讲台下一望，发现学生们欢呼雀跃，仿佛发现了新大陆，大有进一步探究发现的欲望.于是笔者引导学生进行第3)小题的解答.

1.3 提升理解，类比推广

师：现在请生8说说你的解题思路.

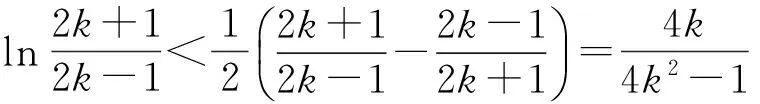
累加可得

即

师：非常好！你是如何想到的呢？

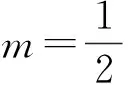
师：如果没有前面第2)小题的提示，直接做第3)小题，该怎么办呢？

笔者刚抛出这一问题，课堂上的学生顿时乐开了花，不少学生异口同声惊呼：原来不用第2)小题也能做出此问题！

师：其他同学有好的解决方案吗？

师：很好！通过大家的分析和探究，原来压轴题是这样命制得来的，只不过在此基础上再加入了参数.这样，我们通过第3)小题的分析和探究，得到了和型数列不等式证明的一种通法，即转化为数列通项大小的比较，希望同学们好好理解.

师：现在提出另外一个问题——数列积型不等式.伟大的科学家开普勒说过：我珍视类比胜过一切，他是我最信赖的主人，他了解自然的所有秘密.下一节课我们将研究这一类型的解法，同学们课后尝试解答下列这道试题：

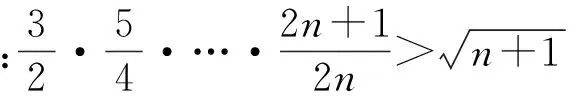
此时下课铃声响了起来，看着学生们继续探究的热情，笔者深感欣慰.第2天，生7兴奋地展示了他的解答：

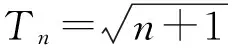
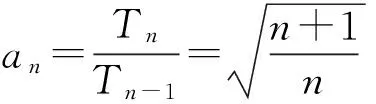
显然当n=1时也成立.因此，原题即证

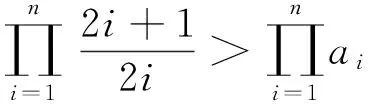
只需证

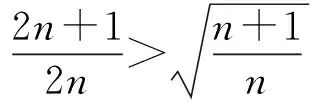
即证

亦即证

显然上式成立，从而

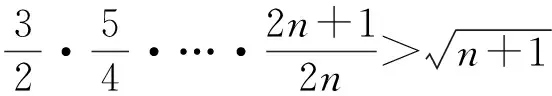
2 教学反思

1)教师在课堂教学时，要注重教学的有效性，注重典型例题的选取，要在充分了解学生学情的基础上开展课堂教学.避免在教学过程中，理想与现实之间的矛盾，做到心中有数、因材施教.这就要求教师在教学之前做大量的工作，如了解学生的基础、激发学生的学习热情、发现学生理解的难点、预设各种教学场景等等.

2)在科学的教学设计基础上，要注重学生的参与，让各类学生都参与到课堂教学的各个环节当中去.如本文所讲评的这道试题，虽然是一道压轴难题，但第1)小题入手容易.教师应多注重学困生信心的提升，多鼓励他们参与到课堂教学中去，使得学生们能感受到教师的关心，并能成长起来.同时应多与中等生互动，因为他们的想法代表了大多数人的想法，能暴露问题症结的所在；他们的问题是课堂教学中最需迫切解决的问题.通过暴露症结，并通过教师的合理引导，激发优秀生大胆猜测、质疑、探究，并通过努力使问题得到解决.这就要改变教师“一手包办、填鸭式”的教学方法，教师应注意创设问题情境，提出富有引导性和挑战性的问题让学生思考、讨论和探究，应呈现数学知识与方法的生成、发展、内化和升华过程，使学生在教师的引导下，了解问题解决的来龙去脉，并达到“举一反三，触类旁通”的教学效果.

3)教师要通过典型的案例，引导学生进行总结，特别是数学思想方法、解题技巧方面的总结.在课堂教学实践中，要有“授人以鱼，不如授人以渔”的理念.如笔者通过第2)小题的讲解，点拨学生总结了导数问题中的惯用处理手法，如：分离参数、分离函数、局部求导、多次求导.再如通过第3)小题的讲解，总结出解答一类数列和型不等式的通法，即转化为数列通项大小的比较，然后再通过类比，引导学生探究数列积型不等式问题的解决.教师要意识到学生数学思想的发生、生成、内化和升华过程的重要性，不可一手包办，要让学生在共同探究中解决问题.教师要意识到学生数学思想的提升是细水长流的过程，不能急功近利，要使学生的能力在长期地接触与体会中得到升华.这就要求教师要有较强的业务能力，不断地进行学习与交流，才能在教学中做到游刃有余.