一道调考试题的5种解法

●李红春

(黄陂区第一中学盘龙校区 湖北武汉 430312)



一道调考试题的5种解法

●李红春

(黄陂区第一中学盘龙校区 湖北武汉 430312)

( )

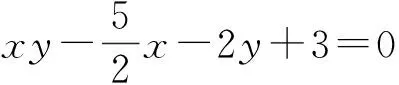
这是湖北省武汉市2015届高三月考的一道试题，是选择题中的把关试题.从学生反馈来看，此题难度颇大.考试中做对的学生普遍采用的是“筛选法”，具体如下：

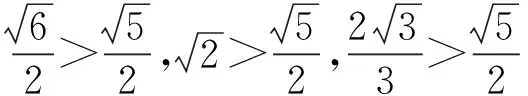
如果该题是填空题或解答题,又该怎么办呢？下面笔者给出5种解法，以飨读者：

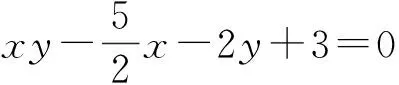
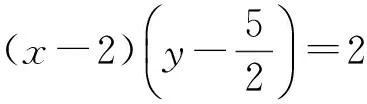
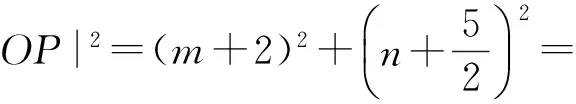
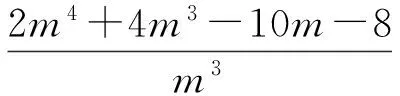
显然m=-1是方程2m4+4m3-10m-8=0的一个根，从而

2m4+4m3-10m-8=

(m+1)(2m3+pm2+qm-8)=0,

分别比较等号左、右2边的三次项和二次项系数，可知

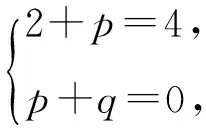
即

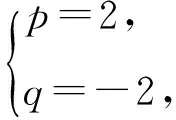
于是 2m4+4m3-10m-8=

(m+1)(2m3+2m2-2m-8).

设g(m)=2m3+2m2-2m-8，其中m∈(-∞,0)，则

g′(m)=6m2+4m-2=2(3m-1)(m+1).

当m∈(-∞,-1)时，g′(m)>0,g(m)递增；当m∈(-1,0)时，g′(m)<0，g(m)递减，从而

g(m)≤g(-1)=-6<0，

于是当m∈(-∞,-1)时，L′(m)<0，L(m)递减；当m∈(-1,0)时，L′(m)>0，L(m)递增，故

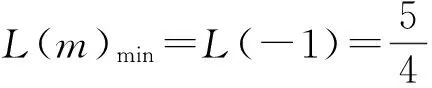
从而

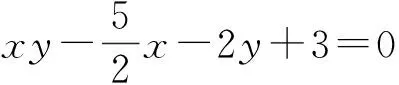
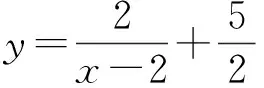
则

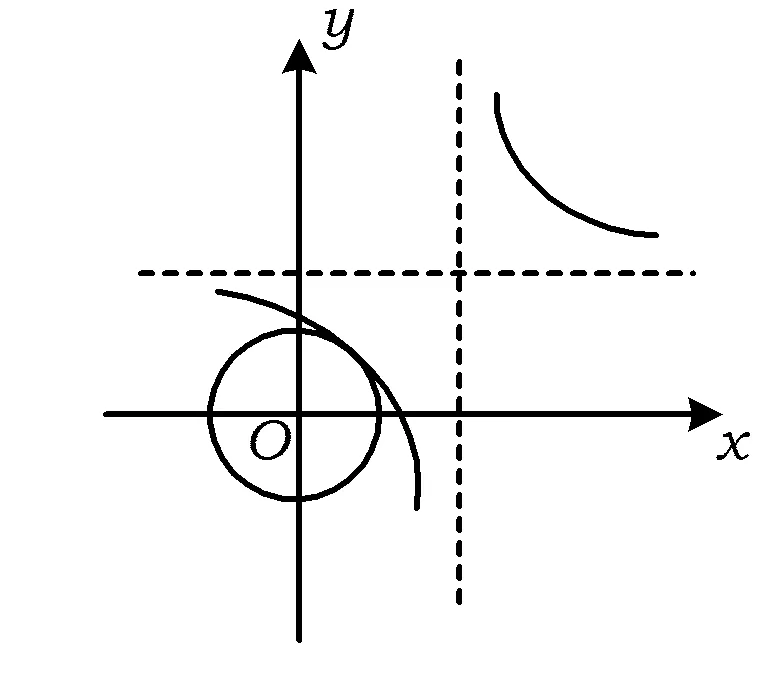
图1

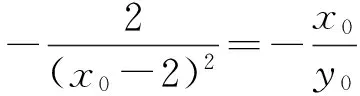
即

2y0=x0(x0-2)2.

即

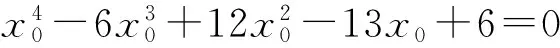
观察该方程可知x0=1是方程的一个根，用待定系数法方程可变形为

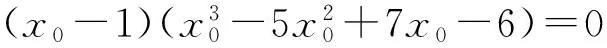
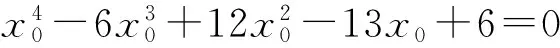
点评 解法1、解法2的共同点是首先要能观察出高次方程的一个根，然后用待定系数法将高次方程进行因式分解，再构造函数借助导数证明其余的因式一定非零．解答过程计算量较大，在紧张的考试氛围中对学生确实是巨大的挑战！

解法3 设点P(x,y)，则

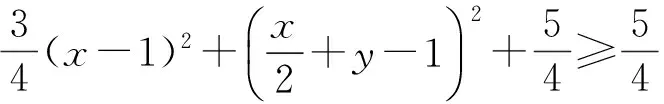
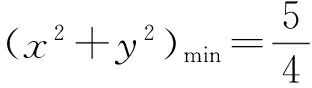
解法4 设点P(x,y)，则

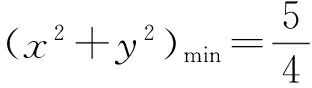
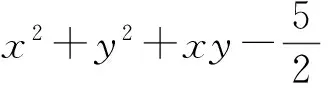
(x2+y2) (16+4)≥(4x+2y)2=(-4x-2y)2=

点评 解法5通过合理配凑，先后灵活运用柯西不等式和均值不等式放缩，简洁地将最值求出.可谓自然天成，解法之妙，让人回味无穷，或许这正是不等式的魅力所在！

本文是云南省曲靖市教育局、曲靖师范学院教育科学规划课题(项目编号：QJQSKT2015001)的研究成果之一.