Level Set方法在Z切石英各向异性湿法刻蚀模拟中的应用

东南大学，江苏南京 211189

一、引言

石英各向异性湿法刻蚀可以用来加工一些特殊结构，如阵列结构、音叉[1]等，在传感器中应用广泛。但也正是由于各向异性的存在，使得石英湿法刻蚀微结构设计对理论和经验要求较高。从工程应用的角度，希望找到一种有效的方法准确模拟石英在加工不同时间段的三维形貌，辅助掩膜设计，充分开发各向异性湿法刻蚀微加工工艺的潜能[2]。

在进行石英各向异性湿法刻蚀形貌数值模拟时，所要追踪模拟的刻蚀界面曲面本身是高维的，同时又因为各向异性的存在，在石英表面法向存在不同的刻蚀速度。这种演变过程与Level Set所描述的曲面变化特点极其吻合。可以将Level Set方法应用到石英各向异性湿法刻蚀模拟中，实现其工程应用价值。

二、Level Set方法

1、Level Set函数构建

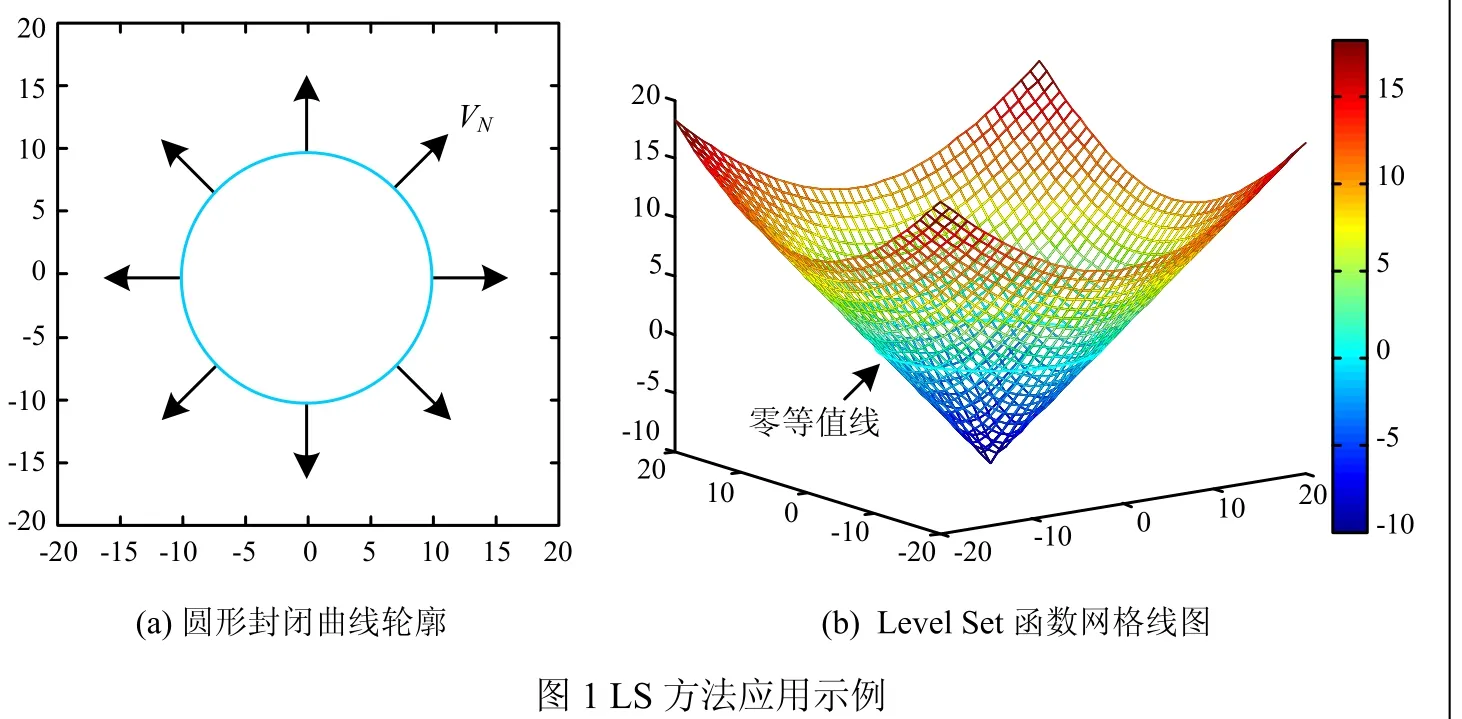
Level Set(LS)方法是Osher 和 Sethian[3]提出的一种隐式追踪运动界面的方法。该方法的主要思想是将需要追踪的运动曲线（曲面）嵌入到高一维的函数中，将其表示为该函数的零等值线（面），这样避免了对追踪曲线（面）的参数化表示，在复杂运动界面追踪和数值模拟中优势明显。

以曲线为例，有许多方法可以实现曲线的追踪，最简单的方法是将曲线直接表示为函数y=f(x,t)。但很多情况下却做不到，如闭合曲线。如图1(a)所示，圆形封闭曲线上一个x会对应多个y值。这时可以根据LS的思想，将圆形曲线嵌入到高一维的函数中，将圆形曲线表示为该函数的零等值线，如图1(b)所示。

LS方法还可以很容易的表示曲线或曲面的拓扑变化，如断裂、融合，这在MEMS加工工艺，如刻蚀、沉积中经常出现。

2、曲面控制方程

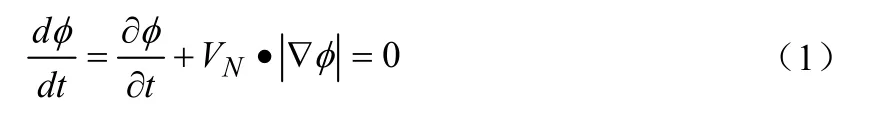
式中，VN—晶面刻蚀速率；

LS函数需要有足够的光滑性，并且在零等值面附近法向单调，可以将LS函数表示为相对于石英刻蚀界面的符号距离函数，即满足。

3、LS方程求解

方程（1）是依赖于时间的一阶双曲型偏微分方程，且是Hamilton-Jacobi方程

的一种具体形式。由于石英各向异性湿法刻蚀的特殊性，Hamilton函数是非凸函数[4]，采用Lax-Friedrichs(LF)格式[5]进行方程的数值求解。（1）式的LF数值求解形式可以写成下式：

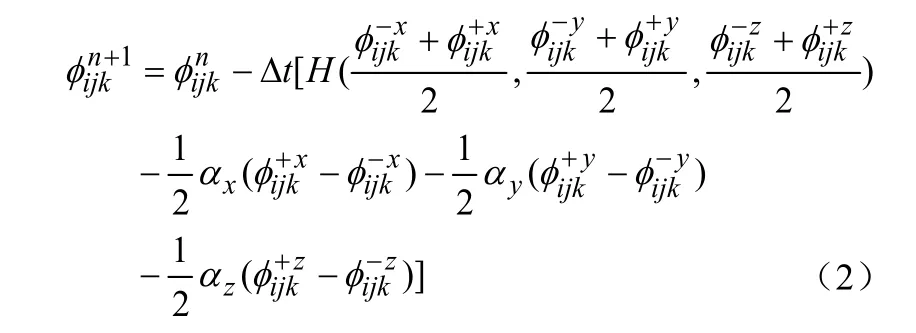
式中，αx,αy,αz—耗散系数，可表示为：

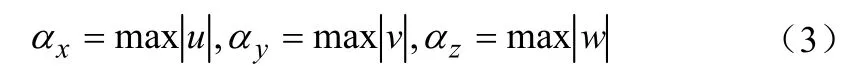
式中，u,v,w—石英晶面刻蚀速率VN在x,y,z三个方向的分量。

根据（2）（3），即可完成对（1）式的数值求解。通过不断更新LS函数，追踪石英刻蚀界面，实现石英刻蚀形貌的实时模拟。

4、LS函数重新初始化

为保证石英刻蚀模拟有较高的精度和稳定性，LS函数必须保持为符号距离函数。但数学上已经证明方程（1）的解并不是符号距离函数[6]。因此，需要每隔一段时间对LS函数进行重新初始化[7]。

LS函数重新初始化有两点要求：

（1）零等值线的位置不变；

（2）初始化后的函数为符号距离函数[7]。

常用的重新初始化方法有直接法、程差方程显示法[8]、偏微分方程隐式迭代法[9]。其中显示方法在零等值面的提取阶段存在数值近似，缺点明显。因此，选用偏微分方程隐式迭代法进行LS函数重新初始化。

偏微分方程隐迭代法重构符号距离函数由Sussman[9]等提出，一般构造如下Hamilton-Jacobi类偏微方程：

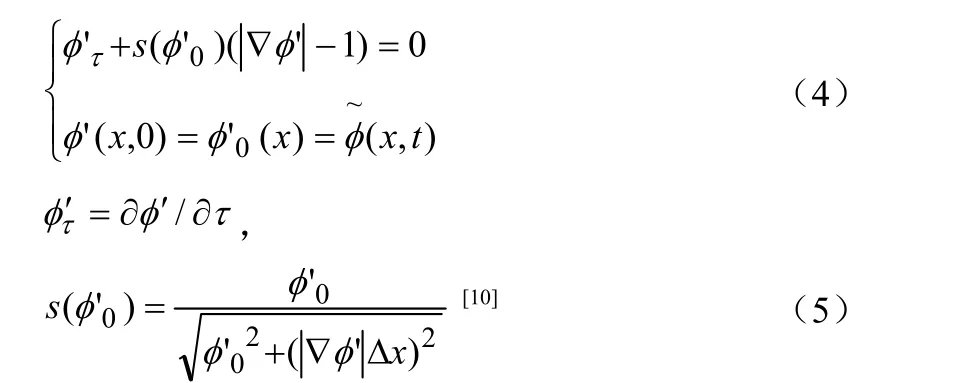
式中，τ—时间；

—初始化前的LS函数；

—初始化后得到的LS函数。

举例说明重新初始化的作用。设椭圆曲线方程如下：

椭圆曲线沿着法向向外扩散。为了追踪曲线的运动，将椭圆曲线嵌入到高一维的LS函数中，如式（7）所示，椭圆曲线为其零等值线：

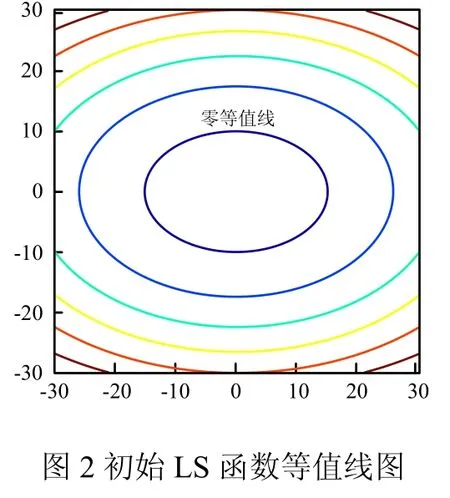
函数（7）的等值线图如图2所示。从图2等值线的分布情况可知初始的LS函数并不是关于零等值线的符号距离函数。

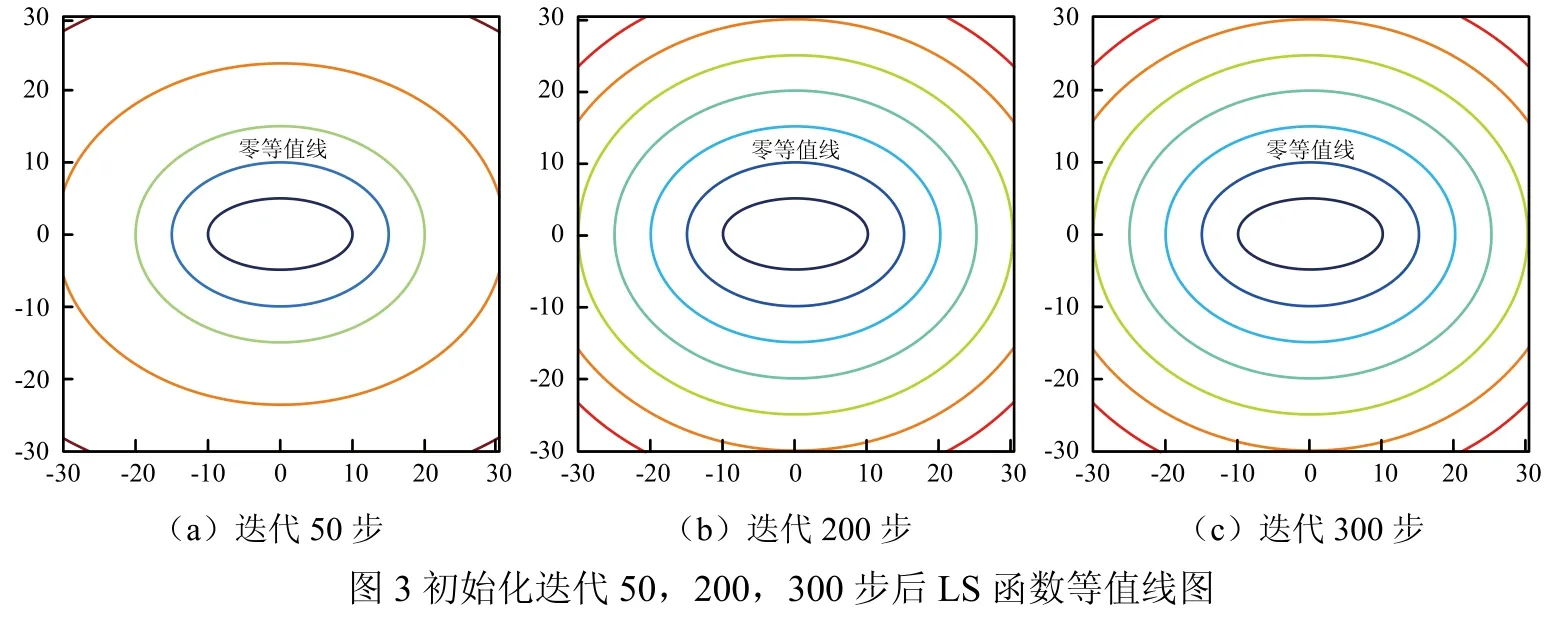
根据式（4）（5）对初始构建的LS函数进行初始化。初始化迭代50, 200, 300步后的函数等值线图如图3所示。

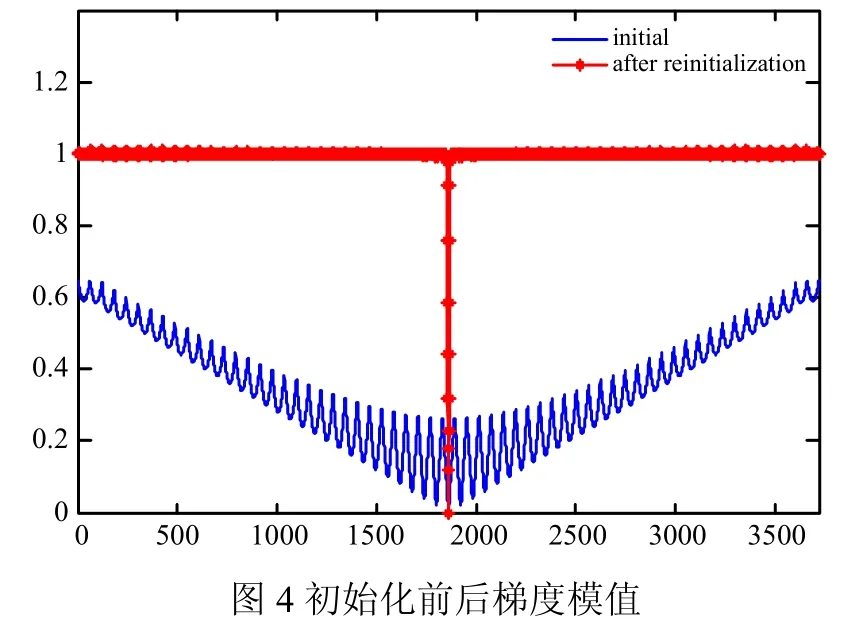
比较迭代200步和300步的等值线图，可以发现迭代200步后方程已经收敛，此时的LS函数为关于零等值线的符号距离函数。观察迭代50步的等值线图可知，在迭代步数较少时，零等值线附近数据点最先满足符号距离函数的要求。石英刻蚀模拟时可以利用这一点，提高计算效率。初始化前后LS函数梯度的模值如图4所示。初始化后除了原点附近的少数几个点外，其他各点处的梯度模值都近似为1达到了初始化的目的。石英刻蚀模拟初始化过程与之类似，只是将曲线转变为了曲面。

三、石英湿法刻蚀模拟

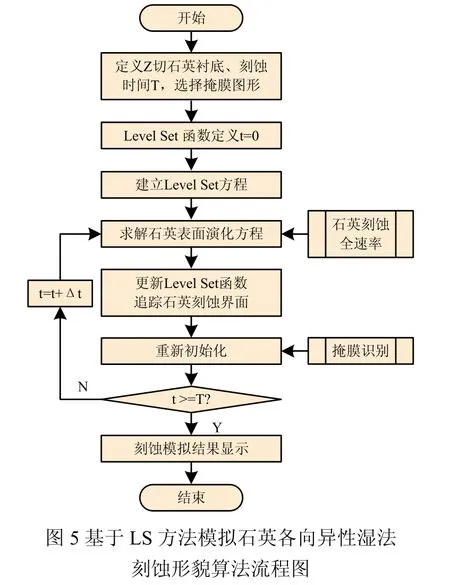
为了借助LS方法准确模拟石英三维刻蚀形貌，首先须获得完整的石英湿法刻蚀全速率图，即VN。Cheng D[11]采用石英半球湿法刻蚀的实验的方法获得了α-石英在80℃饱和氟化氢铵（HF:NH4F=3:2）中的刻蚀全速率图。借助LS方法进行有掩膜石英晶片刻蚀形貌模拟，算法流程如图5所示。根据石英衬底大小、厚度，定义初始LS函数，并构建函数演化方程；LS函数在石英刻蚀速度场中演化；通过追踪LS函数零等值面的位置，确定刻蚀形貌。算法重点在于石英刻蚀速率的对应以及根据掩膜位置进行LS函数的重新初始化。

依据图5所示流程图，在MATLAB软件中开发了石英湿法刻蚀形貌模拟程序。不同掩膜形状Z切石英刻蚀形貌SEM图和模拟结果如图6所示。

槽宽为150μm矩形凹槽刻蚀80min刻蚀形貌如图6(a)所示，侧壁三个主要特征晶面与（0001）面的夹角分别为45°、32°、55°。依据开发出的算法程序模拟得到的侧壁特征晶面，倾角分别为43°、35°、55°，可见模拟结果能很好地反应实际特征晶面，这在工程应用中十分重要。

边长为20μm的三角形凸台实验与模拟结果对比如图6(b)所示。模拟结果较好地反应了实际刻蚀时凸角处特征晶面的演化，体现出了LS方法处理复杂运动界面的能力。

图6(c)为直径200μm圆形凹槽刻蚀80min实验模拟结果图，实验得到的三个交汇面与（0001）面的夹角为35°，模拟值为32°。

从实验图与模拟图的对比可以看出，开发的模拟程序已经可以较为准确地模拟出石英实际刻蚀形貌。在掩膜设计和刻蚀时间参数设置时可以用该模拟程序模拟结果作为参考，减少实验成本。

四、结论

详细介绍了LS方法在石英湿法刻蚀模拟中的应用，包括构建初始LS函数、控制方程、数值解法以及重新初始化。借助开发的石英湿法刻蚀模拟程序，对Z切石英刻蚀形貌进行了模拟。通过和实验结果的对比，表明开发的算法程序是稳定有效的，具有工程应用价值。