等值线“惯性”变化规律的提出及应用

2016-11-21王训飞

地理教学 2016年19期

关键词：等值线等高线惯性

王训飞

（汕头市金山中学, 广东汕头 515073）

等值线“惯性”变化规律的提出及应用

王训飞

（汕头市金山中学, 广东汕头 515073）

等值线的读取和应用是高中地理考查的重点内容。本文通过等值线特征的分析和论证，提出了关于等值线变化的“惯性”定律；并且举例说明，验证了这个规律的正确性。

等值线；趋势线；惯性特征；地理难点

等值线是高中地理常考的重要内容，它的应用广泛，常见的等值线有等高线、等温线、等深线、等潜水位线、等太阳高度线、等盐度线、等地租分布线等。对于考生来讲，需要准确读取等值线，找到等值线所要表示的某个地理要素的变化规律，进而才可以正确地解答相应的问题。

等值线的判读依靠等值线自身的规律，对于较复杂的等值线，一般还需要分析影响等值线所要表示的地理要素的各种因素，辅助判断等值线数值的大小。如果不借助要素的分析，能否单凭等值线自身的规律来解决大多数问题呢？本文试图解决这个问题。

一、等值线的特征论证

1.等值线是一条“趋势线”

从概念上讲，等值线就是数值相等的各点的连线。在等值线上，某个地理要素的数值一定相等。偏离等值线，则数值会有相应的变化。等值线产生的前提是地理要素的变化有一定的规律，以等高线为例，它产生的前提是，在一个区域内，各点的海拔高程是连续变化的。除了陡崖，相邻两点之间的变化是较小的。如果，在区域内任何一点的高程是随机的，那么，就很难或者说没有可能产生等高线。

再举一例说明。在一个班级，一般来讲，学生的座位与身高有关，身高较小者坐在前排，身高较高者坐在后排。这种分布下，我们可以画出“等身高线”的分布。“等身高线”几乎和“排”平行，从第一排到最后一排呈递增趋势。如果学生的座位是完全随机的，身高完全被打乱，每种身高都是“点状分布”，与周围人既不相同也没有规律，则“等身高线”无法绘出。

通过以上两个例子的论证，可以得出，等值线产生的前提是“要素的变化是连续的”。因此，等值线表示的是要素变化的“趋势”。

2.等值线处不可能是“极值”

按照等值线的规律，等值线处有没有可能是最大值或最小值？

以等高线的产生为例，它是水平面与地形相交形成的线。因此，虽然在限定区域内，等高线不一定是闭合的，但是在无限平面内，等高线一定是闭合的。以此类推，任何等值线在无限平面内都是闭合的。

以等高线为例进行说明，如果等值线是最大值，则应当位于山顶处。但是在等高线图上，山顶是一个点，不是一条闭合的等高线，离山顶最近的那条等高线的数值一定小于山顶的海拔。因此，等高线不是海拔最高处。

山脊是相对较高的区域，如果等高线是山脊线的连线，是否表示在这种情况下等高线处比周围都高呢？根据山脊的定义，山脊是海拔较高处向外延伸的狭长的区域，越向外延伸，海拔越低，山脊线的海拔逐渐降低，因此山脊线不可能位于同一条等高线上。

在等高线图上，海拔最低处为盆地或谷地。与上理相同，如果闭合等高线为盆地较低处，则等高线内，海拔一定低于等高线处。根据谷地的定义，谷地是海拔较低处向外延伸的狭长的区域，越向外延伸，海拔越高，山谷线的海拔逐渐升高，因此，山谷线不可能位于同一条等高线上。

因此，等高线处，海拔不可能是最低也不可能是最高。以此类推，所有等值线，都是“过渡线”，等值线处既不可能是最高值也不可能最低值。

3.等值线附近数值不同

在无限接近等值线的两侧，如果数值相同，则存在三种情况：数值都大于等值线，数值都小于等值线，数值都等于等值线。

如果数值都大于等值线，则表示在等值线附近，等值线处是最小值；如果数值都小于等值线，则表示在等值线附近，等值线处是最大值。根据之前论证，等值线处不可能是极值，因此这两种情况不存在。

根据等值线的定义，偏离等值线的附近，数值不可能等于等值线。否则，那些区域都应该在等值线上。

因此，等值线两侧数值一定不相等。也就是说，如果等值线一侧数值大于等值线的数值，另一侧数值一定小于等值线的数值。

4.等值线附近变化趋势一致

按照刚才的论证，等值线一侧数值大于等值线的数值，另一侧小于等值线的值。因此可以得出结论：如果从某一侧向等值线数值减小，则越过等值线后，数值一定会继续减小；如果从某一侧向等值线数值变大，则越过等值线后，数值一定会继续变大。

这个结论的前提是：在无限接近等值线的区域。也就是说，从某一侧向等值线数值减小，则越过等值线后，在极短的距离内，数值一定会继续减小。之后，可能继续减小，也可能增大。无论“一直减小”还是“先减小后变大”，越过等值线后“先减小”是一定的。

如果从某一侧向等值线数值变大，则越过等值线后，“先增大”也是一定的。

二、等值线“惯性”变化规律的提出

通过以上的论证，可以提出等值线“惯性”变化规律：等值线是一条趋势线，它反映了与等值线较近区域的数值变化规律。

等值线“惯性”变化规律的内涵如下：

（1）等值线处在附近区域内不可能是最大值，也不可能是最小值；

（2）等值线两侧的数值一定不同：一侧一定大于等值线的数值，同时另一侧一定小于等值线的数值；

（3）从一侧向等值线处数值递增（递减），则越过等值线后，一定会继续递增（递减）。

规律的应用前提：在无限接近等值线的区域。

三、等值线“惯性”变化规律的应用

总结出等值线的“惯性”变化规律，具有很大的意义：一方面，可以更透彻地理解等值线是一条“趋势线”，它只是反映数值变化的趋势；另一方面，利用这个规律，可以很好地解决关于等值线的许多判读问题，尤其是在没有别的辅助条件可用的时候。现举例说明。

1.“大于大的，小于小的”规律的解析

“大于大的，小于小的”规律是等值线的一条基本规律，即在两条长等值线之间有一条小闭合等值线，如果小闭合等值线的数值与数值较大的那条长等值线的数值相等，则小闭合等值线内任一点的数值大于小闭合等值线的数值；如果小闭合等值线的数值与数值较小的那条长等值线的数值相等，则小闭合等值线内任一点的数值小于小闭合等值线的数值。

这个规律容易记忆，应用起来难度也不大。但是许多学生对从一条长等值线经过小闭合等值线再到另一条等值线之间，数值究竟是如何变化的，一直不太清楚。

图1　

在图1中，在200米等高线到100米等高线之间，经过甲处或乙处的时候，数值究竟是如何变化的？下面应用“惯性”变化规律来进行分析。

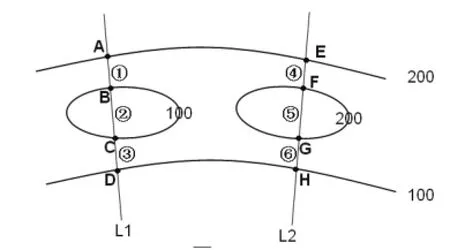
图2　

如图2，L1与各条等值线的的交点分别为A、B、C、D，我们在图中从上向下进行分析：从A处到B处，数值不断下降，因此①段的数值大于100小于200；根据“惯性”变化规律，过B处，会继续下降，但是因为C处也是100，所以②段应当是先下降后上升；再根据“惯性”规律，过C之前是上升的，过C之后会继续上升，因为D处数值为100，所以③段会先上升后下降。

L2段的分析类似，依然在图中从上向下分析：由于E之上数值大于200，所以从上到E处数值下降，因此过了E数值继续下降；因为F数值也是200，所以④段先下降后上升；到达F之前数值上升，到F以后数值继续上升，因为G数值也是200，所以⑤段先上升后下降；再继续推下去，G之前数值下降，G之后数值继续下降，也就是⑥段会持续下降到H处。

得出的垂直变化如图3所示。

图3　

2.一道难题的巧解

2016年深圳市高三年级第一次调研考试的一道选择题：

图4示意某区域河流水系和年降水量分布。读图4，完成10～11小题（第11题与等值线无关，本文只讨论第10题）。

10.图中四条等降水量线之间的①②③④四个区域，年降水量超过400mm的是

A.①②B.②③C.①③D.②④

图4　

参考答案为C。

解析：河流位于山谷；该地位于西风带。①处是山地（较低）；②处是山谷；③处是山腰；④处靠近山顶。高大山地迎风坡的山腰部位降水最多，所以选择C。

本题引起的争论较多，主要是因为地形还原比较困难，所以很难进行判断。

笔者认为，命题者让三条400mm等降水量线相邻，其目的就是考查等值线的变化规律。本题如果抛开地形等影响降水的因素，只研究等值线的变化，利用“惯性”变化特征，就会很容易得出答案。分析如下：

图中从右向左分析，三条400mm等降水量线分别为第一、二、三条400mm等降水量线。④处的数值一定介于200和400之间；从④向第一条400mm等降水量线，数值增加，因此，过了第一条400mm等降水量线后会继续增加，由于再向西出现第二条400mm等降水量线，所以在③处从东向西为先增加后减少，所以③区域的数值大于400；由于从③处到第二条400mm等降水量线数值降低，因此，过了第二条400mm等降水量线后会继续降低，由于第三条400mm等降水量线的出现，所以在②处从东向西数值先降低后增加，因此②区域数值小于400；再依次类推，②区域向第三条400mm等降水量线增加，因此过了第三条400mm等降水量线会继续增加，因此，①区域数值大于400。①、③处数值大于400，得出答案C。

如果根据等值线“惯性”变化规律，“等值线两侧数值不可能相等，一侧一定大于等值线数值，另一侧一定小于等值线数值”，进行如下判断：东侧第一条400mm等降水量线两侧分别为③和④，由于④小于400，则③大于400；③和②位于第二条400mm等降水量线的两侧，③大于400，则②小于400；②和①位于第三条400mm等降水量线的两侧，②小于400，则①大于400。如图5所示。

图5　

从以上的分析可以看出，无论第一种还是第二种分析方法，都比结合地形和风向来考虑要容易得多，而且一步到位得出答案。这种分析应用了等值线自身的变化规律，不需要考虑影响要素，因此简单直接，分析的过程又十分严谨。这样的分析过程又契合命题者的意图。就这道题而言，显然，利用等值线“惯性”变化规律解题是非常行之有效的好办法。